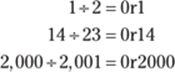Basic Math & Pre-Algebra For Dummies, 2nd Edition (2014)
Part I. Getting Started with Basic Math and Pre-Algebra
Chapter 3. The Big Four: Addition, Subtraction, Multiplication, and Division
In This Chapter
![]() Reviewing addition
Reviewing addition
![]() Understanding subtraction
Understanding subtraction
![]() Viewing multiplication as a fast way to do repeated addition
Viewing multiplication as a fast way to do repeated addition
![]() Getting clear on division
Getting clear on division
When most folks think of math, the first thing that comes to mind is four little (or not-so-little) words: addition, subtraction, multiplication, and division. I call these operations the Big Four all through the book.
In this chapter, I introduce you (or reintroduce you) to these little gems. Although I assume you're already familiar with the Big Four, this chapter reviews these operations, taking you from what you may have missed to what you need to succeed as you move onward and upward in math.
Adding Things Up
Addition is the first operation you find out about, and it's almost everybody's favorite. It's simple, friendly, and straightforward. No matter how much you worry about math, you've probably never lost a minute of sleep over addition. Addition is all about bringing things together, which is a positive goal. For example, suppose you and I are standing in line to buy tickets for a movie. I have $25 and you have only $5. I could lord it over you and make you feel crummy that I can go to the movies and you can't. Or instead, you and I can join forces, adding together my $25 and your $5 to make $30. Now, not only can we both see the movie, but we may even be able to buy some popcorn, too.
Addition uses only one sign — the plus sign (+): Your equation may read 2 + 3 = 5, or 12 + 2 = 14, or 27 + 44 = 71, but the plus sign always means the same thing.
 When you add two numbers together, those two numbers are called addends, and the result is called the sum. So in the first example, the addends are 2 and 3, and the sum is 5.
When you add two numbers together, those two numbers are called addends, and the result is called the sum. So in the first example, the addends are 2 and 3, and the sum is 5.
In line: Adding larger numbers in columns
When you want to add larger numbers, stack them on top of each other so that the ones digits line up in a column, the tens digits line up in another column, and so on. (Chapter 2 has the scoop on digits and place value.) Then add column by column, starting from the ones column on the right. Not surprisingly, this method is called column addition. Here's how you add 55 + 31 + 12. First add the ones column:
![]()
Next, move to the tens column:
![]()
This problem shows you that 55 + 31 + 12 = 98.
Carry on: Dealing with two-digit answers
Sometimes when you're adding a column, the sum is a two-digit number. In that case, you need to write down the ones digit of that number and carry the tens digit over to the next column to the left — that is, write this digit above the column so you can add it with the rest of the numbers in that column. For example, suppose you want to add 376 + 49 + 18. In the ones column, 6 + 9 + 8 = 23, so write down the 3 and carry the 2 over to the top of the tens column:
![]()
Now continue by adding the tens column. In this column, 2 + 7 + 4 + 1 = 14, so write down the 4 and carry the 1 over to the top of the hundreds column:
![]()
Continue adding in the hundreds column:
![]()
This problem shows you that 376 + 49 + 18 = 443.
Take It Away: Subtracting
Subtraction is usually the second operation you discover, and it's not much harder than addition. Still, there's something negative about subtraction — it's all about who has more and who has less. Suppose you and I have been running on treadmills at the gym. I'm happy because I ran 3 miles, but then you start bragging that you ran 10 miles. You subtract and tell me that I should be very impressed that you ran 7 miles farther than I did. (But with an attitude like that, don't be surprised if you come back from the showers to find your running shoes filled with liquid soap!)
As with addition, subtraction has only one sign: the minus sign (−). You end up with equations such as 4 − 1 = 3, and 14 − 13 = 1, and 93 − 74 = 19.
 When you subtract one number from another, the result is called the difference. This term makes sense when you think about it: When you subtract, you find the difference between a higher number and a lower one.
When you subtract one number from another, the result is called the difference. This term makes sense when you think about it: When you subtract, you find the difference between a higher number and a lower one.
 In subtraction, the first number is called the minuend, and the second number is called the subtrahend. But almost nobody ever remembers which is which, so when I talk about subtraction, I prefer to say the first number and the second number.
In subtraction, the first number is called the minuend, and the second number is called the subtrahend. But almost nobody ever remembers which is which, so when I talk about subtraction, I prefer to say the first number and the second number.
One of the first facts you probably heard about subtraction is that you can't take away more than you start with. In that case, the second number can't be larger than the first. And if the two numbers are the same, the result is always 0. For example, 3 − 3 = 0; 11 − 11 = 0; and 1,776 − 1,776 = 0. Later someone breaks the news that you can take away more than you have. When you do, though, you need to place a minus sign in front of the difference to show that you have a negative number, a number below 0:
· 4 − 5 = −1
· 10 − 13 = −3
· 88 − 99 = −11
 When subtracting a larger number from a smaller number, remember the words switch and negate: You switch the order of the two numbers and do the subtraction as you normally would, but at the end, you negate the result by attaching a minus sign. For example, to find 10 − 13, you switch the order of these two numbers, giving you 13 − 10, which equals 3; then you negate this result to get −3. That's why 10 − 13 = −3.
When subtracting a larger number from a smaller number, remember the words switch and negate: You switch the order of the two numbers and do the subtraction as you normally would, but at the end, you negate the result by attaching a minus sign. For example, to find 10 − 13, you switch the order of these two numbers, giving you 13 − 10, which equals 3; then you negate this result to get −3. That's why 10 − 13 = −3.
 The minus sign does double duty, so don't get confused. When you stick a minus sign between two numbers, it means the first number minus the second number. But when you attach it to the front of a number, it means that this number is a negative number.
The minus sign does double duty, so don't get confused. When you stick a minus sign between two numbers, it means the first number minus the second number. But when you attach it to the front of a number, it means that this number is a negative number.
Flip to Chapter 1 to see how negative numbers work on the number line. I also go into more detail on negative numbers and the Big Four operations in Chapter 4.
Columns and stacks: Subtracting larger numbers
To subtract larger numbers, stack one on top of the other as you do with addition. (For subtraction, however, don't stack more than two numbers — put the larger number on top and the smaller one underneath it.) For example, suppose you want to subtract 386 − 54. To start, stack the two numbers and begin subtracting in the ones column: 6 − 4 = 2:
![]()
Next, move to the tens column and subtract 8 − 5 to get 3:
![]()
Finally, move to the hundreds column. This time, 3 − 0 = 3:
![]()
This problem shows you that 386 − 54 = 332.
Can you spare a ten? Borrowing to subtract
Sometimes the top digit in a column is smaller than the bottom digit in that column. In that case, you need to borrow from the next column to the left. Borrowing is a two-step process:
1. Subtract 1 from the top number in the column directly to the left.
Cross out the number you're borrowing from, subtract 1, and write the answer above the number you crossed out.
2. Add 10 to the top number in the column you were working in.
For example, suppose you want to subtract 386 − 94. The first step is to subtract 4 from 6 in the ones column, which gives you 2:
![]()
When you move to the tens column, however, you find that you need to subtract 8 − 9. Because 8 is smaller than 9, you need to borrow from the hundreds column. First, cross out the 3 and replace it with a 2, because 3 − 1 = 2:
![]()
Next, place a 1 in front of the 8, changing it to an 18, because 8 + 10 = 18:
![]()
Now you can subtract in the tens column: 18 − 9 = 9:
![]()
The final step is simple: 2 − 0 = 2:
![]()
Therefore, 386 − 94 = 292.
In some cases, the column directly to the left may not have anything to lend. Suppose, for instance, that you want to subtract 1,002 − 398. Beginning in the ones column, you find that you need to subtract 2 − 8. Because 2 is smaller than 8, you need to borrow from the next column to the left. But the digit in the tens column is a 0, so you can't borrow from there because the cupboard is bare, so to speak:
![]()
 When borrowing from the next column isn't an option, you need to borrow from the nearest nonzero column to the left.
When borrowing from the next column isn't an option, you need to borrow from the nearest nonzero column to the left.
In this example, the column you need to borrow from is the thousands column. First, cross out the 1 and replace it with a 0. Then place a 1 in front of the 0 in the hundreds column:
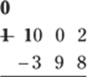
Now cross out the 10 and replace it with a 9. Place a 1 in front of the 0 in the tens column:
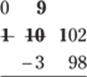
Finally, cross out the 10 in the tens column and replace it with a 9. Then place a 1 in front of the 2:
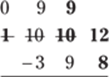
At last, you can begin subtracting in the ones column: 12 − 8 = 4:
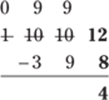
Then subtract in the tens column: 9 − 9 = 0:
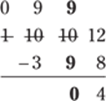
Then subtract in the hundreds column: 9 − 3 = 9:
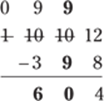
Because nothing is left in the thousands column, you don't need to subtract anything else. Therefore, 1,002 − 398 = 604.
Multiplying
Multiplication is often described as a sort of shorthand for repeated addition. For example,
· 4 × 3 means add 4 to itself 3 times: 4 + 4 + 4 = 12
· 9 × 6 means add 9 to itself 6 times: 9 + 9 + 9 + 9 + 9 + 9 = 54
· 100 × 2 means add 100 to itself 2 times: 100 + 100 = 200
Although multiplication isn't as warm and fuzzy as addition, it's a great timesaver. For example, suppose you coach a Little League baseball team, and you've just won a game against the toughest team in the league. As a reward, you promised to buy three hot dogs for each of the nine players on the team. To find out how many hot dogs you need, you can add 3 together 9 times. Or you can save time by multiplying 3 times 9, which gives you 27. Therefore, you need 27 hot dogs (plus a whole lot of mustard and sauerkraut).
 When you multiply two numbers, the two numbers that you're multiplying are called factors, and the result is the product.
When you multiply two numbers, the two numbers that you're multiplying are called factors, and the result is the product.
 In multiplication, the first number is also called the multiplicand and the second number is the multiplier. But almost nobody ever remembers — or uses — these words.
In multiplication, the first number is also called the multiplicand and the second number is the multiplier. But almost nobody ever remembers — or uses — these words.
Signs of the times
When you're first introduced to multiplication, you use the times sign (×). As you move onward and upward on your math journey, you need to be aware of the conventions I discuss in the following sections.
 The symbol · is sometimes used to replace the symbol ×. For example,
The symbol · is sometimes used to replace the symbol ×. For example,
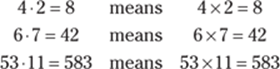
In Parts I through IV of this book, I stick to the tried-and-true symbol × for multiplication. Just be aware that the symbol · exists so that you won't be stumped if your teacher or textbook uses it.
 In math beyond arithmetic, using parentheses without another operator stands for multiplication. The parentheses can enclose the first number, the second number, or both numbers. For example,
In math beyond arithmetic, using parentheses without another operator stands for multiplication. The parentheses can enclose the first number, the second number, or both numbers. For example,
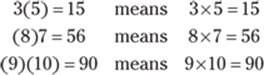
This switch makes sense when you stop to consider that the letter x, which is often used in algebra, looks a lot like the multiplication sign ×. So in this book, when I start using x in Part V, I also stop using × and begin using parentheses without another sign to indicate multiplication.
Memorizing the multiplication table
You may consider yourself among the multiplicationally challenged. That is, you consider being called upon to remember 9 × 7 a tad less appealing than being dropped from an airplane while clutching a parachute purchased from the trunk of some guy's car. If so, then this section is for you.
Looking at the old multiplication table
One glance at the old multiplication table, Table 3-1, reveals the problem. If you saw the movie Amadeus, you may recall that Mozart was criticized for writing music that had “too many notes.” Well, in my humble opinion, the multiplication table has too many numbers.


I don't like the multiplication table any more than you do. Just looking at it makes my eyes glaze over. With 100 numbers to memorize, no wonder so many folks just give up and carry a calculator.
Introducing the short multiplication table
If the multiplication table from Table 3-1 were smaller and a little more manageable, I'd like it a lot more. So here's my short multiplication table, in Table 3-2.

As you can see, I've gotten rid of a bunch of numbers. In fact, I've reduced the table from 100 numbers to 28. I've also shaded 11 of the numbers I've kept.
Is just slashing and burning the sacred multiplication table wise? Is it even legal? Well, of course it is! After all, the table is just a tool, like a hammer. If a hammer's too heavy to pick up, then you need to buy a lighter one. Similarly, if the multiplication table is too big to work with, you need a smaller one. Besides, I've removed only the numbers you don't need. For example, the condensed table doesn't include rows or columns for 0, 1, or 2. Here's why:
· Any number multiplied by 0 is 0 (people call this trait the zero property of multiplication).
· Any number multiplied by 1 is that number itself (which is why mathematicians call 1 the multiplicative identity — because when you multiply any number by 1, the answer is identical to the number you started with).
· Multiplying by 2 is fairly easy; if you can count by 2s — 2, 4, 6, 8, 10, and so forth — you can multiply by 2.
The rest of the numbers I've gotten rid of are redundant. (And not just redundant, but also repeated, extraneous, and unnecessary!) For example, any way you slice it, 3 × 5 and 5 × 3 are both 15 (you can switch the order of the factors because multiplication is commutative — see Chapter 4 for details). In my condensed table, I've simply removed the clutter.
So what's left? Just the numbers you need. These numbers include a gray row and a gray diagonal. The gray row is the 5 times table, which you probably know pretty well. (In fact, the 5s may evoke a childhood memory of running to find a hiding place on a warm spring day while one of your friends counted in a loud voice: 5, 10, 15, 20, …)
The numbers on the gray diagonal are the square numbers. As I discuss in Chapter 1, when you multiply any number by itself, the result is a square number. You probably know these numbers better than you think.
Getting to know the short multiplication table
In about an hour, you can make huge strides in memorizing the multiplication table. To start, make a set of flash cards that give a multiplication problem on the front and the answer on the back. They may look like Figure 3-1.
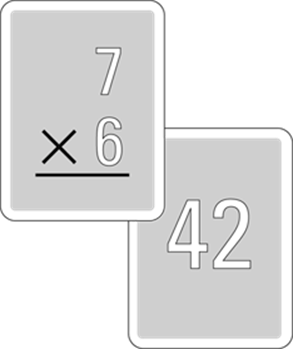
Illustration by Wiley, Composition Services Graphics
Figure 3-1: Both sides of a flash card, with 7 × 6 on the front and 42 on the back.
Remember, you need to make only 28 flash cards — one for every example in Table 3-2. Split these 28 into two piles — a “gray” pile with 11 cards and a “white” pile with 17. (You don't have to color the cards gray and white; just keep track of which pile is which, according to the shading in Table 3-2.) Then begin:
1. 5 minutes: Work with the gray pile, going through it one card at a time. If you get the answer right, put that card on the bottom of the pile. If you get it wrong, put it in the middle so you get another chance at it more quickly.
2. 10 minutes: Switch to the white pile and work with it in the same way.
3. 15 minutes: Repeat Steps 1 and 2.
Now take a break. Really — the break is important to rest your brain. Come back later in the day and do the same thing.
When you're done with this exercise, you should find going through all 28 cards with almost no mistakes to be fairly easy. At this point, feel free to make cards for the rest of the standard times table — you know, the cards with all the 0, 1, and 2 times tables on them and the redundant problems — mix all 100 cards together, and amaze your family and friends.
 To the nines: A slick trick
To the nines: A slick trick
Here's a trick to help you remember the 9 times table. To multiply any one-digit number by 9,
1. Subtract 1 from the number being multiplied by 9 and jot down the answer.
For example, suppose you want to multiply 7 × 9. Here, 7 – 1 = 6.
2. Jot down a second number so that, together, the two numbers you wrote add up to 9. You've just written the answer you were looking for.
Adding, you get 6 + 3 = 9. So 7 × 9 = 63.
As another example, suppose you want to multiply 8 × 9:
· 8 – 1 = 7
· 7 + 2 = 9
So 8 × 9 = 72.
This trick works for every one-digit number except 0 (but you already know that 0 × 9 = 0).
Double digits: Multiplying larger numbers
The main reason to know the multiplication table is so you can more easily multiply larger numbers. For example, suppose you want to multiply 53 × 7. Start by stacking these numbers on top of one another with a line underneath, and then multiply 3 by 7. Because 3 × 7 = 21, write down the 1 and carry the 2:
![]()
Next, multiply 7 by 5. This time, 5 × 7 = 35. But you also need to add the 2 that you carried over, which makes the result 37. Because 5 and 7 are the last numbers to multiply, you don't have to carry, so write down the 37 — you find that 53 × 7 = 371:
![]()
When multiplying larger numbers, the idea is similar. For example, suppose you want to multiply 53 by 47. (The first few steps — multiplying by the 7 in 47 — are the same, so I pick up with the next step.) Now you're ready to multiply by the 4 in 47. But remember that this 4 is in the tens column, so it really means 40. So to begin, put a 0 directly under the 1 in 371:
![]()
This 0 acts as a placeholder so that this row is arranged properly. (See Chapter 1 for more about placeholding zeros.)
 When multiplying by larger numbers with two digits or more, use one placeholding zero when multiplying by the tens digit, two placeholding zeros when multiplying the hundreds digit, three zeros when multiplying by the thousands digit, and so forth.
When multiplying by larger numbers with two digits or more, use one placeholding zero when multiplying by the tens digit, two placeholding zeros when multiplying the hundreds digit, three zeros when multiplying by the thousands digit, and so forth.
Now you multiply 3 × 4 to get 12, so write down the 2 and carry the 1:
![]()
Continuing, multiply 5 × 4 to get 20, and then add the 1 that you carried over, giving a result of 21:
![]()
To finish, add the two products (the multiplication results):
![]()
So 53 × 47 = 2,491.
Doing Division Lickety-Split
The last of the Big Four operations is division. Division literally means splitting things up. For example, suppose you're a parent on a picnic with your three children. You've brought along 12 pretzel sticks as snacks, and want to split them fairly so that each child gets the same number (don't want to cause a fight, right?).
Each child gets four pretzel sticks. This problem tells you that
![]()
As with multiplication, division also has more than one sign: the division sign (÷) and the fraction slash (/) or fraction bar (—). So some other ways to write the same information are
12/3 = 4 and ![]()
Whichever way you write it, the idea is the same: When you divide 12 pretzel sticks equally among three people, each person gets 4 of them.
 When you divide one number by another, the first number is called the dividend, the second is called the divisor, and the result is the quotient. For example, in the division from the earlier example, the dividend is 12, the divisor is 3, and the quotient is 4.
When you divide one number by another, the first number is called the dividend, the second is called the divisor, and the result is the quotient. For example, in the division from the earlier example, the dividend is 12, the divisor is 3, and the quotient is 4.
Whatever happened to the division table?
Considering how much time teachers spend on the multiplication table, you may wonder why you've never seen a division table. For one thing, the multiplication table focuses on multiplying all the one-digit numbers by each other. This focus doesn't work too well for division because division usually involves at least one number that has more than one digit.
Besides, you can use the multiplication table for division, too, by reversing the way you normally use the table. For example, the multiplication table tells you that 6 × 7 = 42. You can reverse this equation to give you these two division problems:
![]()
Using the multiplication table in this way takes advantage of the fact that multiplication and division are inverse operations. I discuss this important idea further in Chapter 4.
Making short work of long division
In the olden days, knowing how to divide large numbers — for example, 62,997 ÷ 843 — was important. People used long division, an organized method for dividing a large number by another number. The process involved dividing, multiplying, subtracting, and dropping numbers down.
But face it — one of the main reasons the pocket calculator was invented was to save 21st-century humans from ever having to do long division again.
Having said that, I need to add that your teacher and math-crazy friends may not agree. Perhaps they just want to make sure you're not completely helpless if your calculator disappears somewhere into your backpack or your desk drawer or the Bermuda Triangle. But if do you get stuck doing page after page of long division against your will, you have my deepest sympathy.
I will go this far, however: Understanding how to do long division with some not-too-horrible numbers is a good idea. In this section, I give you a good start with long division, telling you how to do a division problem that has a one-digit divisor.
Recall that the divisor in a division problem is the number that you're dividing by. When you're doing long division, the size of the divisor is your main concern: Small divisors are easy to work with, and large ones are a royal pain.
Suppose you want to find 860 ÷ 5. Start off by writing the problem like this:
![]()
Unlike the other Big Four operations, long division moves from left to right. In this case, you start with the number in the hundreds column (8). To begin, ask how many times 5 goes into 8 — that is, what's 8 ÷ 5? The answer is 1 (with a little bit left over), so write 1 directly above the 8. Now multiply 1 × 5 to get 5, place the answer directly below the 8, and draw a line beneath it:
![]()
Subtract 8 − 5 to get 3. (Note: After you subtract, the result should always be smaller than the divisor. If not, you need to write a higher number above the division symbol.) Then bring down the 6 to make the new number 36:
![]()
These steps are one complete cycle — to complete the problem, you just need to repeat them. Now ask how many times 5 goes into 36 — that is, what's 36 ÷ 5? The answer is 7 (with a little left over). Write 7 just above the 6, and then multiply 7 × 5 to get 35; write the answer under 36:
![]()
Now subtract to get 36 − 35 = 1; bring down the 0 next to the 1 to make the new number 10:
![]()
Another cycle is complete, so begin the next cycle by asking how many times 5 goes into 10 — that is, 10 ÷ 5. The answer this time is 2. Write down the 2 in the answer above the 0. Multiply to get 2 × 5 = 10, and write this answer below the 10:
![]()
Now subtract 10 − 10 = 0. Because you have no more numbers to bring down, you're finished, and here's the answer (that is, the quotient):
![]()
So 860 ÷ 5 = 172.
This problem divides evenly, but many don't. The following section tells you what to do when you run out of numbers to bring down, and Chapter 11 explains how to get a decimal answer.
Getting leftovers: Division with a remainder
Division is different from addition, subtraction, and multiplication in that having a remainder is possible. A remainder is simply a portion left over from the division.
 The letter r indicates that the number that follows is the remainder.
The letter r indicates that the number that follows is the remainder.
For example, suppose you want to divide seven candy bars between two people without breaking any candy bars into pieces (too messy). So each person receives three candy bars, and one candy bar is left over. This problem shows you the following:
· 7 ÷ 2 = 3 with a remainder of 1, or 3r1
In long division, the remainder is the number that's left when you no longer have numbers to bring down. The following equation shows that 47 ÷ 3 = 15r2:
![]()
 Note that when you're doing division with a small dividend and a large divisor, you always get a quotient of 0 and a remainder of the number you started with:
Note that when you're doing division with a small dividend and a large divisor, you always get a quotient of 0 and a remainder of the number you started with: