Burn Math Class: And Reinvent Mathematics for Yourself (2016)

4. On Circles and Giving Up

4.6. The Dilemma

4.6.1Too Many Directions

There is yet another unfortunate fact related to coordinates, though it is not the fault of the coordinates themselves. The unfortunate fact is: there are too many directions. No matter how we choose to draw our coordinates, not everything will point in the direction of one of our axes. Let’s illustrate the problem by thinking about finding your way home. Imagine you’re setting off in a boat to search for distant lands across the ocean. You’d rather not get lost at sea, so you decide to bring a map. If you were to travel exactly west for your entire journey, then finding your way home would be no problem. If you went some distance d, you would just turn around and go the same distance d in the opposite direction. Even though east-west is one of the “axes” of the coordinate systems we commonly use, the above idea works for any direction. If you only went a distance d in a straight line, then you would just turn around and go that same distance in the opposite direction. Unfortunately, just going straight isn’t always an option. You might turn to avoid a rock, you might turn by accident, etc. Given that you’ve changed directions, how far away are you now? You need a way to combine information from different directions.

At first, the problem might seem like one we’ve already solved. If we write x_k for the number of miles we traveled in the E-W direction on day number k, then after n days, the number of miles we’ve gone in the E-W direction is just x₁ + x₂ + · · · + x_n, or (to abbreviate all that addition using the notation we talked about in Chapter 2)

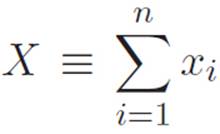
Similarly, if we write y_k for the number of miles we traveled in the N-S direction on day number k, then the number of miles we’ve gone in the N-S direction after n days is just

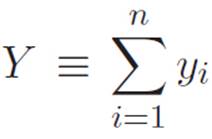
The numbers X and Y are the total distance we’ve traveled in the E-W and the N-S directions, respectively. If we want to figure out how far we are from home, just use the formula for shortcut distances to compute .

However, even if we knew how to compute square roots (which we don’t yet), doing so actually wouldn’t solve our problem! Our real problem is that we don’t usually receive our information in the form of the numbers x_k and y_k. We don’t know what they are. When we’re actually navigating through the actual world, we find that Nature doesn’t hand us the numbers x_k and y_k on each day. That is, we’re not handed information about how far we’ve gone in the E-W and N-S directions. What we probably have is distances (lengths) and directions (angles). That is, at best we would have something like Figure 4.4, and maybe a list like this:

Day 1: 12 miles east

Day 2: 7 miles north-east

Day 3: 10 miles east-north-east

It’s not clear how to figure out how far we’ve gone. The main problem is that the information we were given is phrased in terms of distances traveled in directions other than our axes: there are too many possible directions. If only the information we had were phrased in terms of how far we had gone on each day in the horizontal and vertical map directions (i.e., how far east-west, and how far north-south), then we would know what to do. That’s the much simpler problem we solved above, using the numbers x_k and y_k and the formula for shortcut distances.

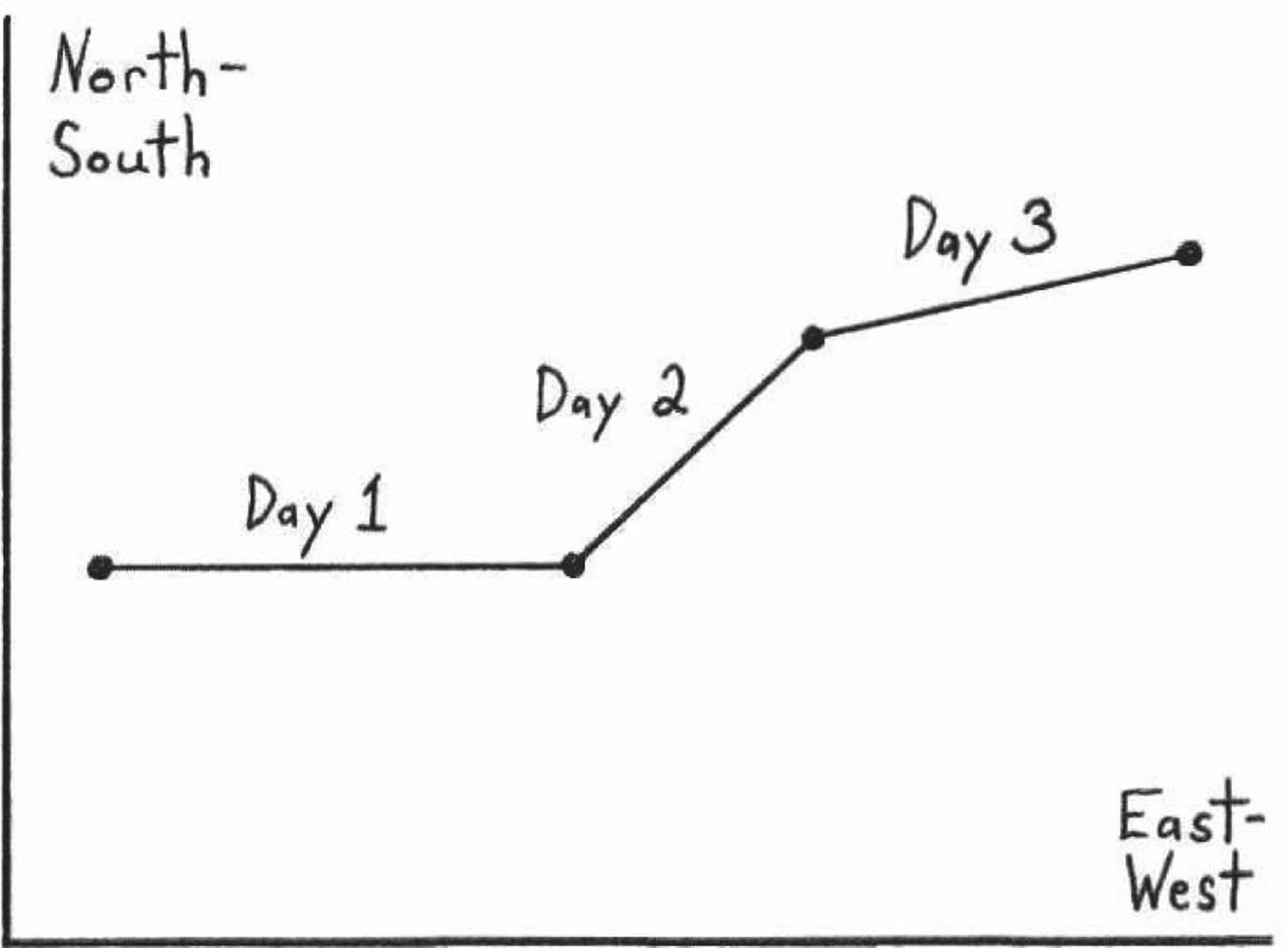
Figure 4.4: We need to figure out how to combine information about different directions.

Figure 4.4 shows us the problem, and Figure 4.5 shows us why the problem is really just a problem of translation. If we could figure out how to translate the “distance and angle” information on each day into “horizontal and vertical” information, then we could solve the problem by reducing it to the one we solved above.

We’ve reduced the navigation problem to a slightly simpler abstract problem. At this point, we can forget the three-part path in Figures 4.4 and 4.5. Why? Because if only we had in our possession a method of translating distance and angle information into horizontal and vertical information, we would just have to use that three times, and we could (in principle) solve our navigation problem.

Looking at the dilemma in this more abstract form, as a problem of translation, we can see that the essence of the dilemma had nothing to do with navigation per se. It’s a problem about translating information phrased in the language of distances and angles into equivalent information in the language of our coordinate system — the coordinate system we built from two perpendicular directions. Having recognized that the problem is really more general than we might have initially expected, let’s try to think about it in a more abstract setting.

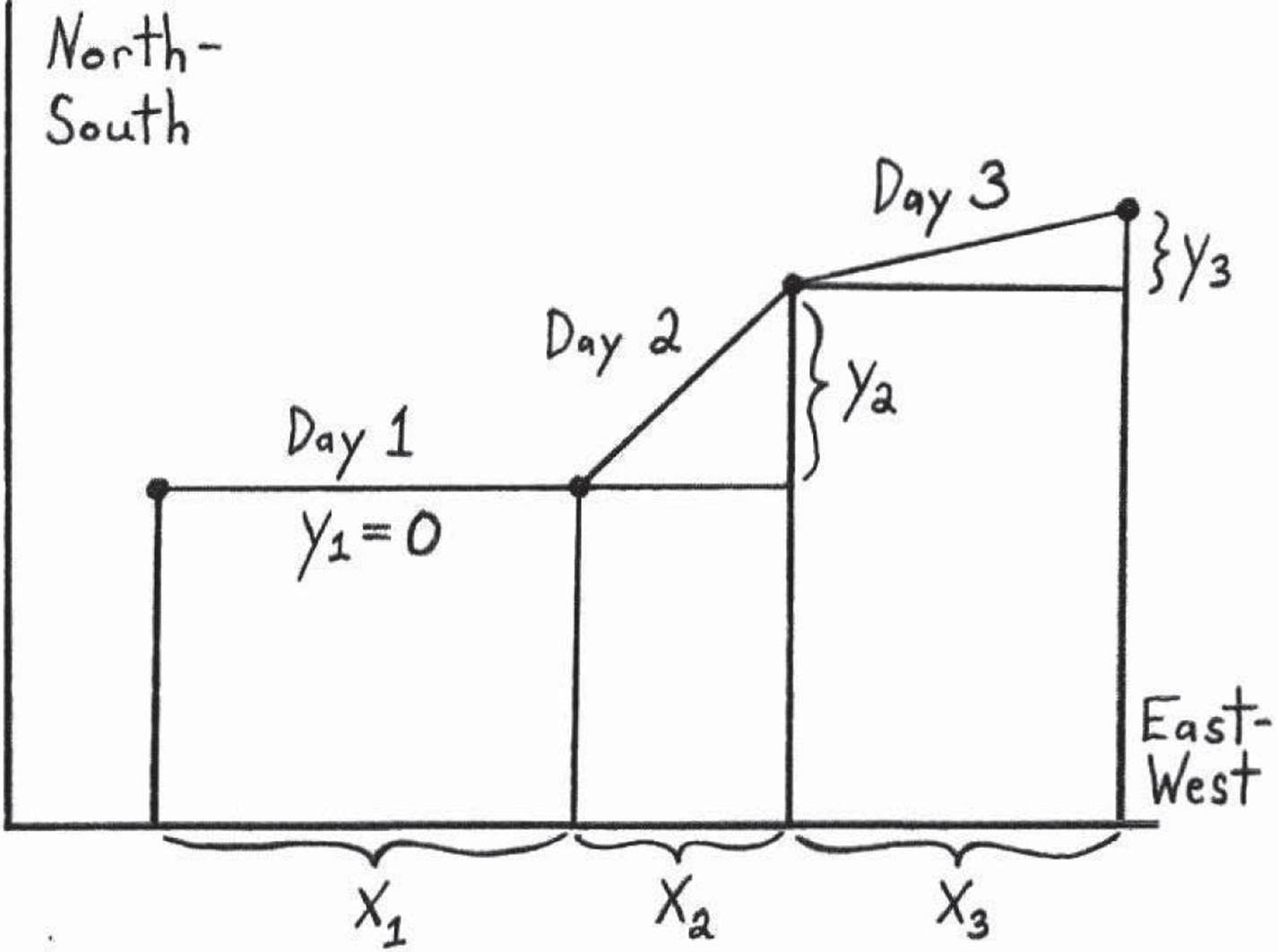
Figure 4.5: Not getting lost at sea would be easy if only we could translate “distance and angle” information into “horizontal and vertical” information.

4.6.2The Dilemma in Abstract Form

Strangely, we’ve managed to simplify our problem by making it more abstract, rather than more concrete. However, we still don’t know what to do. The dilemma can be summarized as follows:

The Reverse Shortcut Distance Dilemma:

Suppose we’ve already picked a coordinate system, so we’ve got two directions, v and h (“vertical” and “horizontal”). Someone hands us a straight thing of length ℓ, which may be pointing in any direction. Is there a way of describing how much of it is in the vertical direction, and how much is in the horizontal direction?

The problem is depicted in Figure 4.6. At this point, we don’t have a clue how to tackle this problem. However, we can choose some abbreviations. Let’s write H for the amount that’s in the horizontal direction, and V for the amount that’s in the vertical direction. At this point, all we can write is

H (thing) = ?

V (thing) = ?

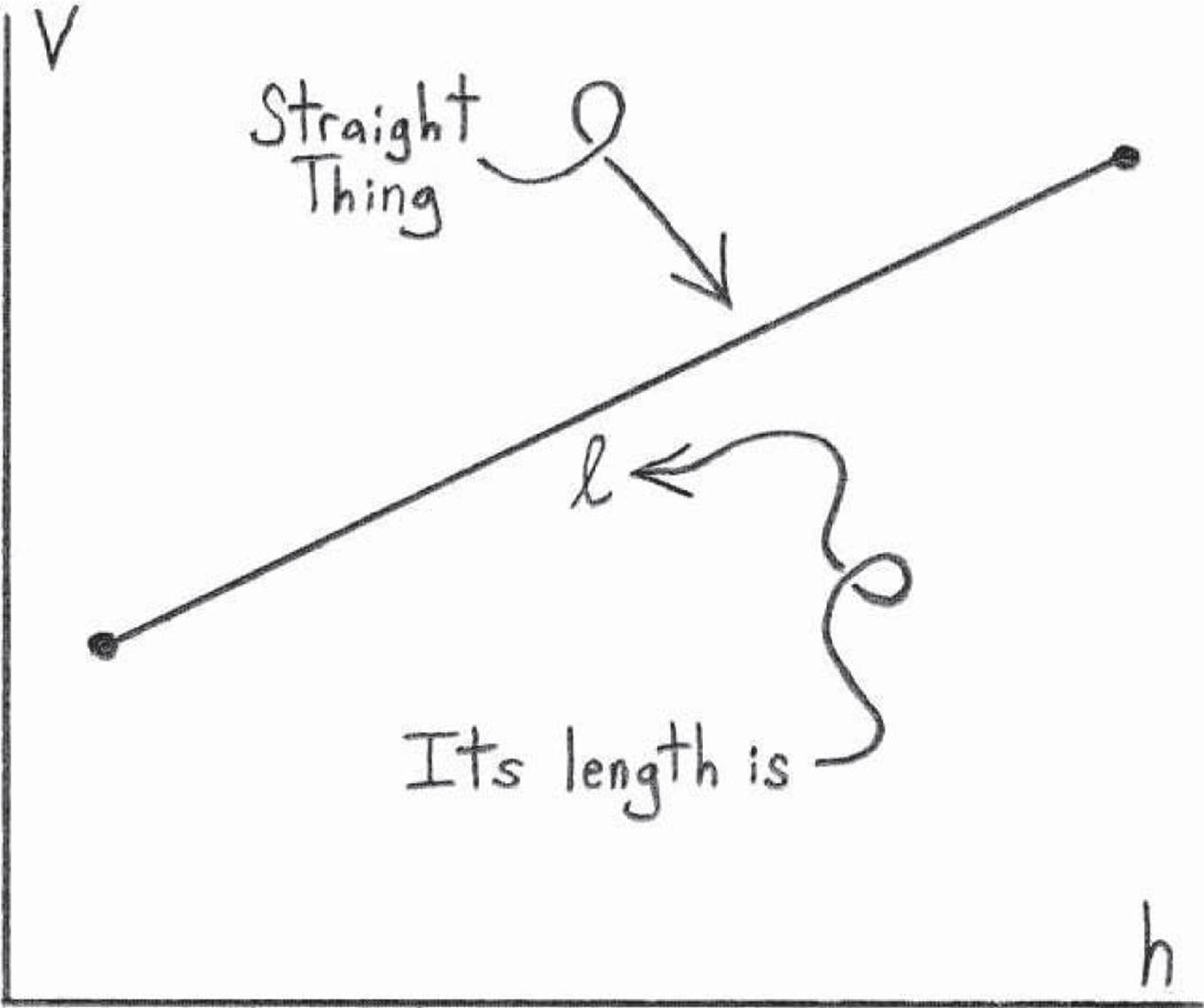
Figure 4.6: If someone hands us a straight thing with length ℓ that isn’t pointing in the direction of our coordinates, can we figure out how much of it is pointing in the horizontal and vertical directions?

Is there anything else we know? Well, no matter what the length of the thing,² if it’s completely vertical, then H should be zero, and if it’s completely horizontal, then V should be zero. However, for all the different amounts of tiltedness in between vertical and horizontal, we have no idea what to do. It would be nice if we had some way of measuring the amount of tiltedness. Is there any way to do this?

I realize this may seem like a lazy choice of words. Apologies for using the word “thing,” but the term “line segment” makes me tired. “Stick” didn’t feel right either. The term “thing” is admittedly a bit generic and abstract, but then again, so is mathematics.

In a sense, we already invented a way to measure an amount of tiltedness. That’s what we did when we invented slope. However, recall that our definition of slope for lines was , where v was the vertical distance between two points on the line, and h was the horizontal distance. So as promising as it might have seemed to measure the tiltedness of our straight thing by using its slope or steepness, this idea is putting the cart before the horse. After all, our dilemma is to figure out the horizontal and vertical pieces, so our solution to the problem had better not contain them. We need some other way to talk about direction.

What do we mean by “direction” in everyday life? Well, if we stand up and start “changing direction” (i.e., turning around), then we end up turning in a circle, so maybe we can talk about direction in terms of circles. There are lots of ways to do this, just like there are lots of ways to measure length. We could choose to say that a complete turn, all the way around, is an angle of 1. If we did this, then turning halfway around would be an angle of , turning to your left would be an angle of , and so on. That’s perfectly fine, and to be honest, I have no idea why the standard textbooks don’t do this. Granted, it would make some expressions look more complicated, but it would also make others look simpler. For whatever reason, there are two common conventions for measuring angles, and they’re basically the only ones you’ll ever see. The first is to measure angles in “degrees,” which is a system in which a complete turn counts as 360 degrees. I assume that the only reason for this system is that 360 happens to be divisible by a lot of numbers. The more common system is to measure angles in units of the radius of a circle. This is a weird concept at first, but it makes a reasonable amount of sense. In the above dialogue, we found that our give-up number # was the same as Mathematics’s give-up number , which was originally defined like this:

where d is the distance across a circle. If r is the “radius” of the circle, then d = 2r, so we could rewrite Mathematics’s definition of like this:

which just says that no matter how big your circle is, it takes copies of the radius to walk all the way around it. For whatever reason, the most common convention for measuring angles is not to count a full turn as 1 or as 360 but as . We still don’t know which particular number is,³ but if we’re using this convention, then half a turn would be an angle of , a quarter of a turn would be , and so on. We’ll use this convention for measuring angles throughout the book.

Recall that is the number that textbooks call π. We’re keeping our ignorance in plain view until we’ve gotten rid of it, by choosing to call this number until we figure out a way to calculate its numerical value.

Let’s use the abbreviation α for “angle,” because α is the Greek a, and this reminds us of what we’re talking about.⁴ Having invented the concept of angles, we can now state our dilemma in slightly different language.

Why α and not a? Well, in some ways a would be a better choice. The Greek letter isn’t necessary. However, although we frequently take advantage of the freedom to invent our own notation, it’s also worthwhile to occasionally mention the standard notation, and even use it when it’s not too horrible. For whatever reason, there’s an unspoken convention in mathematics (and in physics) to represent stuff involving angles using Greek letters. Why? No idea. Textbooks often represent angles using the letters θ, φ, α, and β; angular velocity is usually represented by ω; torque (the angular version of force, in physics) is represented by τ; and so on. While using lots of letters from different alphabets can sometimes make things a bit more pretentious, in this case the convention isn’t so bad. So, since α looks enough like a to remind us of what we’re talking about, let’s go ahead and allow it into our universe, for now.

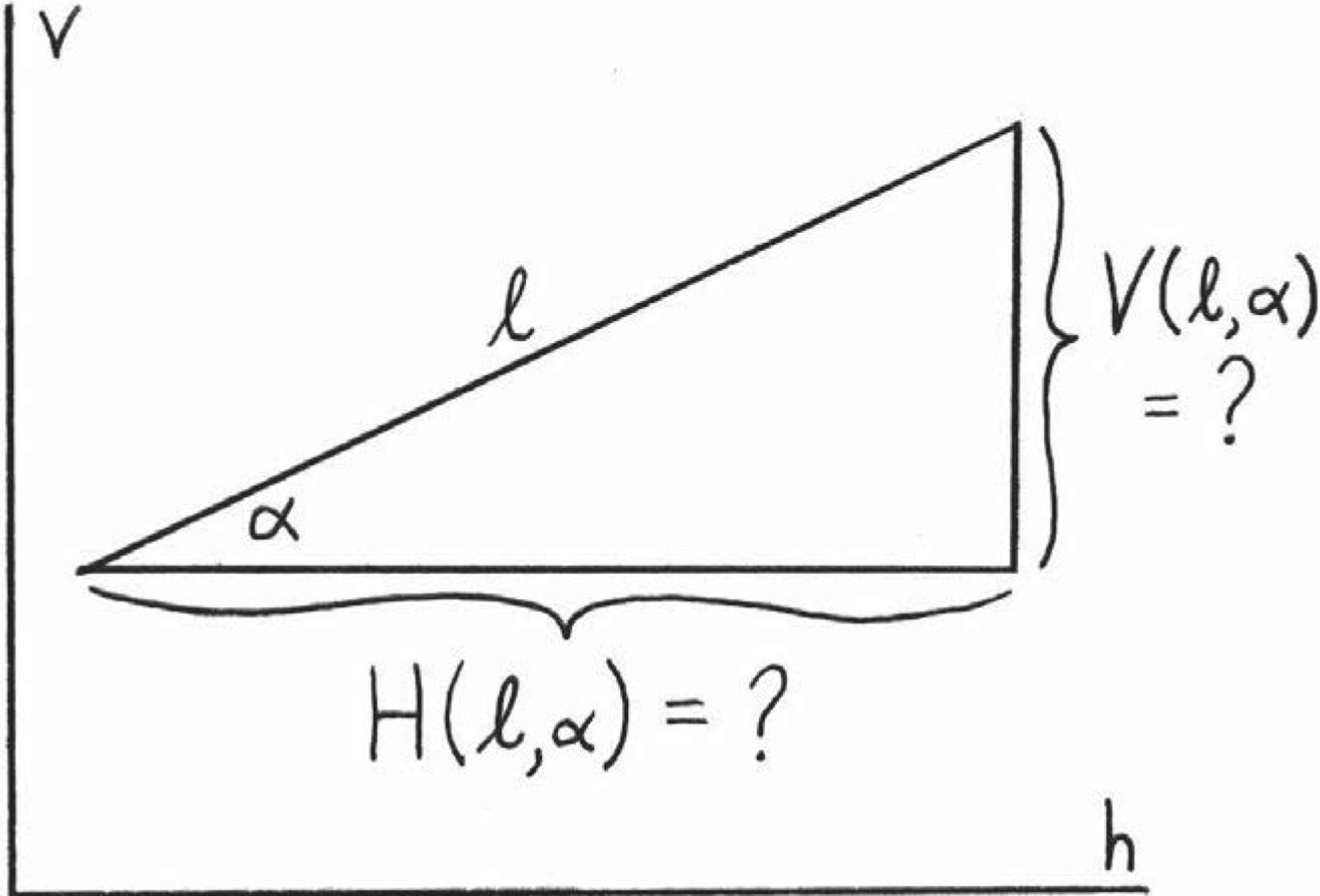
Figure 4.7: Now that we know what angles are, we can redraw the abstract form of our dilemma like this.

The Reverse Shortcut Distance Dilemma:

Suppose we’ve already picked a coordinate system, so we’ve got two directions v and h, which stand for “vertical” and “horizontal.” Someone hands us a straight thing of length ℓ, which is at some angle α measured counterclockwise from the positive horizontal axis. Is there a way of describing how much is in the vertical direction and how much is in the horizontal direction?

This new way of phrasing the dilemma is depicted in Figure 4.7. Now instead of writing H(thing) and V (thing), we can write:

H(ℓ, α) = ?

V (ℓ, α) = ?

Even though we can’t solve the full dilemma yet, it’s not too hard to see that different dilemmas are related to each other. Here’s what I mean. What if someone handed us two different versions of this problem with the same angle α, but the lengths were different? For example, in addition to the original problem, suppose we’re handed another problem in which the length is 2ℓ rather than ℓ:

H(2ℓ, α) = ?

V(2ℓ, α) = ?

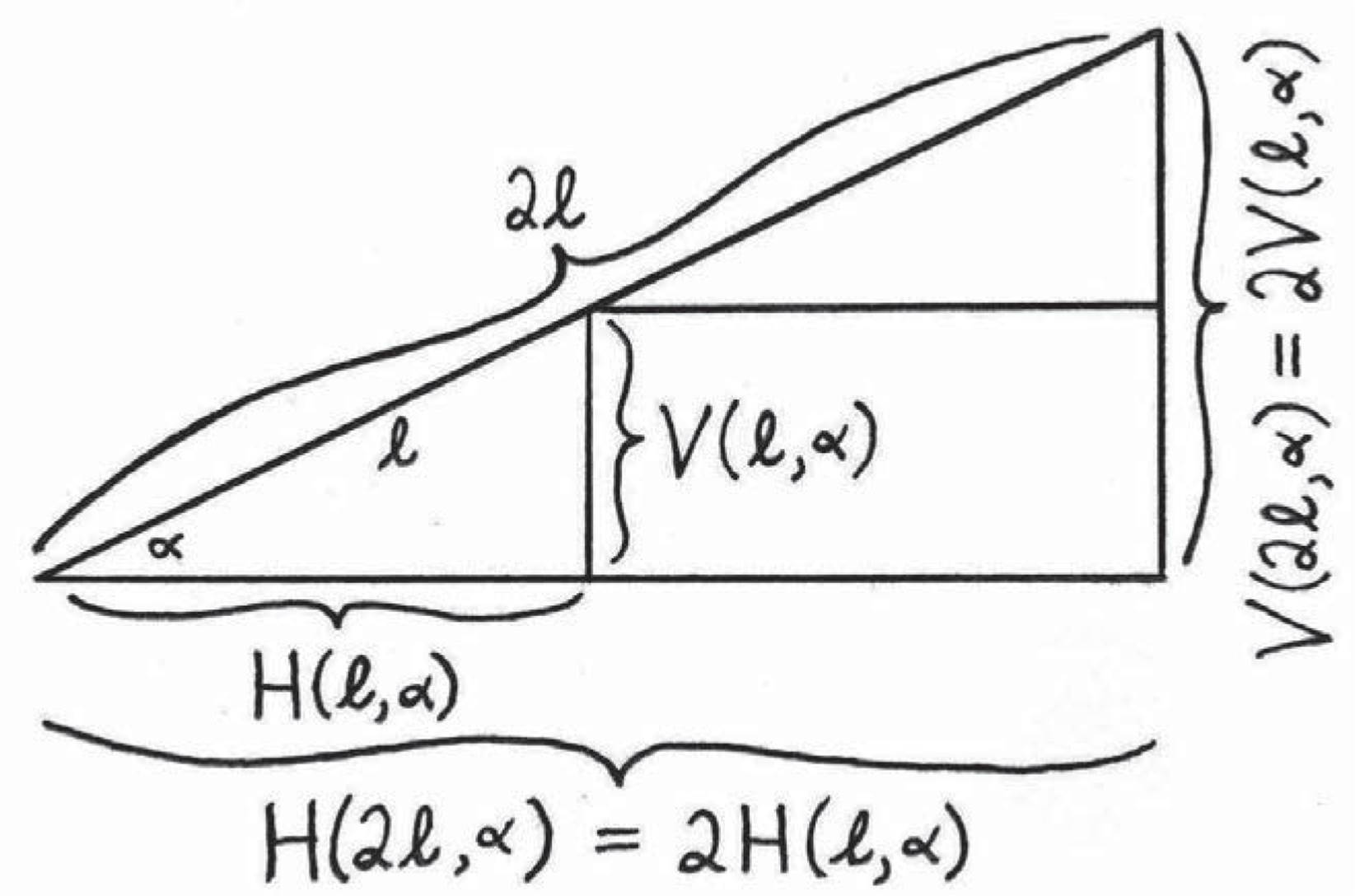
Figure 4.8: Two related dilemmas. We still don’t know H(ℓ, α) or V(ℓ, α), but we can see a relationship between problems with the same angle and different lengths. For example, H(2ℓ, α) = 2H(ℓ, α).

This situation is similar to the problem involving # and with which we began this chapter. We can’t solve either dilemma, but we can convince ourselves that two problems we can’t solve are related to each other. Simply glancing at Figure 4.8 makes it clear that

H(2ℓ, α) = 2H(ℓ, α)

V(2ℓ, α) = 2V(ℓ, α)

To put it another way, we have essentially reduced the 2ℓ problem to the ℓ problem, even though we can’t solve either one! Moreover, there is nothing special about the number 2 in this argument. It shouldn’t be hard to imagine a picture like Figure 4.8 that would demonstrate the same pattern forH(3ℓ, α) and V(3ℓ, α). An analogous picture could be drawn for any whole number n, as well as simple non-whole numbers like or , so it’s not difficult to convince ourselves that the same pattern should hold for any number #. That is, for any number #, we have:

H(#ℓ, α) = #H(ℓ, α)

V (#ℓ, α) = #V(ℓ, α)

These two facts allow us to perform a clever hack that will get us much closer to solving our dilemma. That is, if the above two facts are true for all numbers #, then we can use these facts on the length ℓ itself, treating ℓ as ℓ · 1, to get

H (ℓ, α) = ℓH (1, α)

V (ℓ, α) = ℓV (1, α)

This is great. What these two sentences say is that we only need to solve our dilemma for one particular length. We chose a length of 1, but we easily could have chosen any other number. For example, we would be equally justified in writing , or anything else of this form. We chose 1 for purely aesthetic reasons. The important thing isn’t which length we choose, but the fact that the “length” part of the dilemma isn’t really a dilemma after all. If we can figure out H(1, α) and V (1, α), then we can instantly figure out H(ℓ, α) and V(ℓ, α) for any other length we might encounter.

Let’s use this new insight to make some better abbreviations. Since the length slot can be dealt with so easily, we don’t need to write two slots in H and V after all. Let’s abbreviate:

H(α) ≡ H(1, α)

V(α) ≡ V(1, α)

Then, if we ever feel like writing the lengths explicitly, we can write H(ℓ, α) = ℓH(α), and so on.