Calculus II For Dummies, 2nd Edition (2012)

Part II. Indefinite Integrals

Chapter 7. Trig Substitution: Knowing All the (Tri)Angles

In This Chapter

Memorizing the basic trig integrals

Integrating powers of sines and cosines, tangents and secants, and cotangents and cosecants

Understanding the three cases for using trig substitution

Trig substitution is another technique to throw in your ever-expanding bag of integration tricks. It allows you to integrate functions that contain radicals of polynomials such as and other similar difficult functions.

Trig substitution may remind you of variable substitution, which I discuss in Chapter 5. With both types of substitution, you break the function that you want to integrate into pieces and express each piece in terms of a new variable. With trig substitution, however, you express these pieces as trig functions.

So before you can do trig substitution, you need to be able to integrate a wider variety of products and powers of trig functions. The first few parts of this chapter give you the skills that you need. After that, I show you how to use trig substitution to express complicated-looking radical functions in terms of trig functions.

Integrating the Six Trig Functions

You already know how to integrate sin x and cos x from Chapter 4, but for completeness, here are the integrals of all six trig functions:

Please commit these to memory — you need them! For practice, you can also try differentiating each result to show why each of these integrals is correct.

Integrating Powers of Sines and Cosines

Later in this chapter, when I show you trig substitution, you need to know how to integrate powers of sines and cosines in a variety of combinations. In this section, I show you what you need to know.

Odd powers of sines and cosines

You can integrate any function of the form sin^m x cosⁿ x when m is odd, for any real value of n. For this procedure, keep in mind the handy trig identity

sin² x + cos² x = 1. For example, here’s how you integrate

1. Peel off a sin x and place it next to the dx:

2. Apply the trig identity sin² x = 1 – cos² x to express the rest of the sines in the function as cosines:

3. Use the variable substitution u = cos x and du = –sin x dx:

Now that you have the function in terms of powers of u, the worst is over. You can expand the function out, turning it into a polynomial. This is just algebra:

To continue, use the Sum Rule and Constant Multiple Rule to separate this into four integrals, as I show you in Chapter 4. Don’t forget to distribute that minus sign to all four integrals!

At this point, you can evaluate each integral separately using the Power Rule:

Finally, use u = cos x to reverse the variable substitution:

Notice that when you substitute back in terms of x, the power goes next to the cos rather than next to the x, because you’re raising the entire function cos x to a power. (See Chapter 2 if you’re unclear about this point.)

Similarly, you integrate any function of the form sin^m x cosⁿ x when n is odd, for any real value of m. These steps are practically the same as those in the previous example. For instance, here’s how you integrate sin^–4 x cos⁹ x:

1. Peel off a cos x and place it next to the dx:

2. Apply the trig identity cos² x = 1 – sin² x to express the rest of the cosines in the function as sines:

3. Use the variable substitution u = sin x and du = cos x dx:

At this point, you can distribute the function to turn it into a polynomial and then integrate it as I show you in the previous example.

Even powers of sines and cosines

To integrate sin² x and cos² x, use the two half-angle trig identities that I show you in Chapter 2:

For example, here’s how you integrate cos² x:

1. Use the half-angle identity for cosine to rewrite the integral in terms of cos 2x:

2. Use the Constant Multiple Rule to move the denominator outside the integral:

3. Distribute the function and use the Sum Rule to split it into several integrals:

4. Evaluate the two integrals separately:

As a second example, here’s how you integrate sin² x cos⁴ x:

1. Use the two half-angle identities to rewrite the integral in terms of cos 2x:

2. Use the Constant Multiple Rule to move the denominators outside the integral:

3. Distribute the function and use the Sum Rule to split it into several integrals:

4. Evaluate the resulting odd-powered integrals by using the procedure from the earlier section “Odd powers of sines and cosines,” and evaluate the even-powered integrals by returning to Step 1 of the previous example. I perform these integrations in one step, so you can see the result:

With the integration behind you, use algebra to simplify the result. To start, combine the first and third terms, and second and fifth terms:

Now distribute the result:

Integrating Powers of Tangents and Secants

When you’re integrating powers of tangents and secants, here’s the rule to remember: Eeeven powers of seeecants are eeeasy. The threee Es in the keeey words should help you remember this rule. By the way, odd powers of tangents are also easy. You’re on your own remembering this fact!

In this section, I show you how to integrate tan^m x secⁿ x for all positive integer values of m and n. You use this skill later in this chapter, when I show you how to do trig substitution.

Even powers of secants with tangents

To integrate tan^m x secⁿ x when n is even — for example, tan⁸ x sec⁶ x — follow these steps:

1. Peel off a sec² x and place it next to the dx:

2. Use the trig identity 1 + tan² x = sec² x to express the remaining secant factors in terms of tangents:

3. Use the variable substitution u = tan x and du = sec² x dx:

At this point, the integral is a polynomial, and you can evaluate it as I show you in Chapter 4.

Odd powers of tangents with secants

To integrate tan^m x secⁿ x when m is odd — for example, tan⁷ x sec⁹ x — follow these steps:

1. Peel off a tan x and a sec x and place them next to the dx:

2. Use the trig identity tan² x = sec² x – 1 to express the remaining tangent factors in terms of secants:

3. Use the variable substitution u = sec x and du = sec x tan x dx:

At this point, the integral is a polynomial, and you can evaluate it as I show you in Chapter 4.

Odd powers of tangents without secants

To integrate tan^m x when m is odd, use a trig identity to convert the function to sines and cosines as follows:

After that, you can integrate using the procedure from the earlier section, “Odd powers of sines and cosines.”

Even powers of tangents without secants

To integrate tan^m x when m is even — for example, tan⁸ x — follow these steps:

1. Peel off a tan² x and use the trig identity tan² x = sec² x – 1 to express it in terms of tan x:

2. Distribute to split the integral into two separate integrals:

3. Evaluate the first integrals using the procedure I show you in the earlier section “Even powers of secants with tangents.”

4. Return to Step 1 to evaluate the second integral.

Even powers of secants without tangents

To integrate secⁿ x when n is even — for example, sec⁴ x — follow these steps:

1. Use the trig identity 1 + tan² x = sec² x to express the function in terms of tangents:

2. Distribute and split the integral into three or more integrals:

3. Integrate all powers of tangents using the procedures from the sections on powers of tangents without secants.

Odd powers of secants without tangents

This is the hardest case, so fasten your seat belt. To integrate secⁿ x when n is odd — for example, sec³ x — follow these steps:

1. Peel off a sec x:

2. Use the trig identity 1 + tan² x = sec² x to express the remaining secants in terms of tangents:

3. Distribute and split the integral into two or more integrals:

4. Evaluate the first integral:

You can omit the constant C because you still have an integral that you haven’t evaluated yet — just don’t forget to put it in at the end.

5. Integrate the second integral by parts by differentiating tan x and integrating sec x tan x (see Chapter 6 for more on integration by parts):

At this point, notice that you’ve shown the following equation to be true:

6. Follow the algebraic procedure that I outline in Chapter 6.

First, substitute the variable I for the integral on both sides of the equation:

Now solve this equation for I:

Now you can substitute the integral back for I. Don’t forget, however, that you need to add a constant to the right side of this equation, to cover all possible solutions to the integral:

That’s your final answer. I truly hope that you never have to integrate sec⁵ x, let alone higher odd powers of a secant. But if you do, the basic procedure I outline here will provide you with a value for in terms of . Good luck!

Even powers of tangents with odd powers of secants

To integrate tan^m x secⁿ x when m is even and n is odd, transform the function into an odd power of secants, and then use the method that I outline in the previous section “Odd powers of secants without tangents.”

For example, here’s how you integrate tan⁴ x sec³ x:

1. Use the trusty trig identity tan² x = sec² x – 1 to convert all the tangents to secants:

2. Distribute the function and split the integral using the Sum Rule:

3. Solve the resulting odd-powered integrals using the procedure from “Odd powers of secants without tangents.”

Unfortunately, this procedure brings you back to the most difficult case in this section. Fortunately, most teachers are fairly merciful when you’re working with these functions, so you probably won’t have to face this integral on an exam. If you do, however, you have my deepest sympathy.

Integrating Powers of Cotangents and Cosecants

The methods for integrating powers of cotangents and cosecants are very close to those for tangents and secants, which I show you in the preceding section. For example, in the earlier section “Even powers of secants with tangents,” I show you how to integrate tan⁸ x sec⁶ x.

Here’s how to integrate cot⁸ x csc⁶ x:

1. Peel off a csc² x and place it next to the dx:

2. Use the trig identity 1 + cot² x = csc² x to express the remaining cosecant factors in terms of cotangents:

3. Use the variable substitution u = cot x and du = –csc² x dx:

At this point, the integral is a polynomial, and you can evaluate it as I show you in Chapter 4.

Notice that the steps here are virtually identical to those for tangents and secants. The biggest change here is the introduction of a minus sign in Step 3. So to find out everything you need to know about integrating cotangents and cosecants, try all the examples in the previous section, but switch every tangent to a cotangent and every secant to a cosecant.

Sometimes, knowing how to integrate cotangents and cosecants can be useful for integrating negative powers of other trig functions — that is, powers of trig functions in the denominator of a fraction.

For example, suppose that you want to integrate . The methods that I outline earlier don’t work very well in this case, but you can use trig identities to express it as cotangents and cosecants:

I show you more about this method in the next section “Integrating Weird Combinations of Trig Functions.”

Integrating Weird Combinations of Trig Functions

You don’t really have to know how to integrate every possible trig function to pass Calculus II. If you can do all the techniques that I introduce earlier in this chapter — and I admit that’s a lot to ask! — you’ll be able to handle most of what your professor throws at you with ease. You’ll also have a good shot at hitting any curveballs that come at you on an exam.

But in case you’re nervous about the exam and would rather study than worry, in this section I show you how to integrate a wider variety of trig functions. I don’t promise to cover all possible trig functions exhaustively. But I do give you a few additional ways to think about and categorize trig functions that could help you when you’re in unfamiliar territory.

You can express every product of powers of trig functions, no matter how weird, as the product of any pair of trig functions. The three most useful pairings (as you may guess from earlier in this chapter) are sine and cosine, tangent and secant, and cotangent and cosecant. Table 7-1 shows you how to express all six trig functions as each of these pairings.

For example, look at the following function:

As it stands, you can’t do much to integrate this monster. But try expressing it in terms of each possible pairing of trig functions:

As it turns out, the most useful pairing for integration in this case is cot⁶ x csc² x. No fraction is present — that is, both terms are raised to positive powers — and the cosecant term is raised to an even power, so you can use the same basic procedure that I show you in the earlier section “Even powers of secants with tangents.”

Using Trig Substitution

Trig substitution is similar to variable substitution (which I discuss in Chapter 5), using a change in variable to turn a function that you can’t integrate into one that you can. With variable substitution, you typically use the variable u. With trig substitution, however, you typically use the variable θ.

Trig substitution allows you to integrate a whole slew of functions that you can’t integrate otherwise. These functions have a special, uniquely scary look about them and are variations on these three themes:

(a² – bx²)ⁿ

(a² + bx²)ⁿ

(bx² – a²)ⁿ

Trig substitution is most useful when n is or a negative number — that is, for hairy square roots and polynomials in the denominator of a fraction. When n is a positive integer, your best bet is to express the function as a polynomial and integrate it as I show you in Chapter 4.

In this section, I show you how to use trig substitution to integrate functions like these. But, before you begin, take this simple test:

Trig substitution is:

A) Easy and fun — even a child can do it!

B) Not so bad when you know how.

C) About as attractive as drinking bleach.

I wish I could tell you that the answer is A, but then I’d be a big liarmouth and you’d never trust me again. So I admit that trig substitution is less fun than a toga party with a hot date. At the same time, your worst trig substitution nightmares don’t have to come true, so please put the bottle of bleach back in the laundry room.

I have the system right here, and if you follow along closely, I give you the tool that you need to make trig substitution mostly a matter of filling in the blanks. Trust me — have I ever lied to you?

Distinguishing three cases for trig substitution

Trig substitution is useful for integrating functions that contain three very recognizable types of polynomials in either the numerator or denominator. Table 7-2 lists the three cases that you need to know about.

The first step to trig substitution is being able to recognize and distinguish these three cases when you see them.

Knowing the formulas for differentiating the inverse trig functions can help you remember these cases:

Note that the differentiation formula for arcsin x contains a polynomial that looks like the sine case: a constant minus x². The formula for arctan x contains a polynomial that looks like the tangent case: a constant plus x². And the formula for arcsec x contains a polynomial that looks like the secant case: x² minus a constant. So if you already know these formulas, you don’t have to memorize any additional information.

Integrating the three cases

Trig substitution is a five-step process:

1. Draw the trig substitution triangle for the correct case.

2. Identify the separate pieces of the integral (including dx) that you need to express in terms of .

3. Express these pieces in terms of trig functions of .

4. Rewrite the integral in terms of and evaluate it.

5. Substitute x for in the result.

Don’t worry if these steps don’t make much sense yet. In this section, I show you how to do trig substitution for each of the three cases.

The sine case

When the function you’re integrating includes a term of the form (a² – bx²)ⁿ, draw your trig substitution triangle for the sine case. For example, suppose that you want to evaluate the following integral:

This is a sine case, because a constant minus a multiple of x² is being raised to a power . Here’s how you use trig substitution to handle the job:

1. Draw the trig substitution triangle for the correct case.

Figure 7-1 shows you how to fill in the triangle for the sine case. Notice that the radical goes on the adjacent side of the triangle. Then, to fill in the other two sides of the triangle, I use the square roots of the two terms inside the radical — that is, 2 and x. I place 2 on the hypotenuse and x on the opposite side.

You can check to make sure that this placement is correct by using the Pythagorean theorem: .

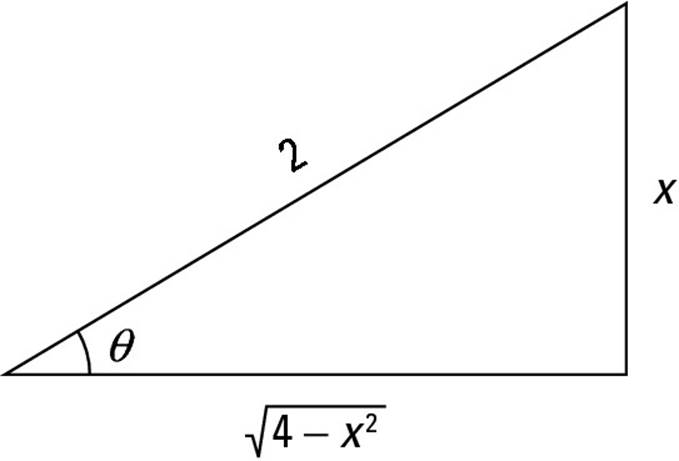
2. Identify the separate pieces of the integral (including dx) that you need to express in terms of .

In this case, the function contains two separate pieces that contain x:

and dx.

3. Express these pieces in terms of trig functions of .

This is the real work of trig substitution, but when your triangle is set up properly, this work becomes a lot easier. In the sine case, all trig functions should be sines and cosines.

To represent the radical portion as a trig function of θ, first build a fraction using the radical as the numerator and the constant 2 as the denominator. Then set this fraction equal to the appropriate trig function:

Because the numerator is the adjacent side of the triangle and the denominator is the hypotenuse , this fraction is equal to cos θ.

Now a little algebra gets the radical alone on one side of the equation:

Next, you want to express dx as a trig function of θ. To do so, build another fraction with the variable x in the numerator and the constant 2 in the denominator. Then set this fraction equal to the correct trig function:

This time, the numerator is the opposite side of the triangle and the denominator is the hypotenuse , so this fraction is equal to sin θ.

Now solve for x and then differentiate:

x = 2 sin θ

dx = 2 cos θ dθ

4. Rewrite the integral in terms of and evaluate it:

Knowing how to evaluate trig integrals really pays off here. I cut to the chase in this example, but earlier in this chapter (in “Integrating Powers of Sines and Cosines”), I show you how to integrate all sorts of trig functions like this one:

= 2θ + sin 2θ + C

5. To change those two terms into x terms, reuse the following equation:

So here’s a substitution that gives you an answer:

This answer is perfectly valid, so, technically speaking, you can stop here. However, some professors frown upon the nesting of trig and inverse trig functions, so they’ll prefer a simplified version of . To find this, start by applying the double-angle sine formula (see Chapter 2) to sin 2θ:

Now use your trig substitution triangle to substitute values for sin θ and cos θ in terms of x:

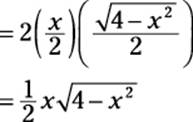
To finish, substitute this expression for that problematic second term to get your final answer in a simplified form:

2 θ + sin 2 θ + C

The tangent case

When the function you’re integrating includes a term of the form (a² + x²)ⁿ, draw your trig substitution triangle for the tangent case. For example, suppose that you want to evaluate the following integral:

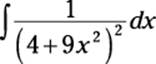
This is a tangent case, because a constant plus a multiple of x² is being raised to a power (–2). Here’s how you use trig substitution to integrate:

1. Draw the trig substitution triangle for the tangent case.

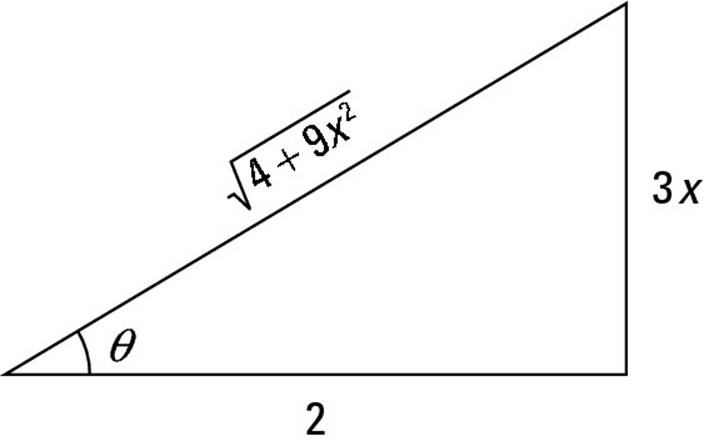
Figure 7-2 shows you how to fill in the triangle for the tangent case. Notice that the radical of what’s inside the parentheses goes on the hypotenuse of the triangle. Then, to fill in the other two sides of the triangle, use the square roots of the two terms inside the radical — that is, 2 and 3x. Place the constant term 2 on the adjacent side and the variable term 3x on the opposite side.

With the tangent case, make sure not to mix up your placement of the variable and the constant.

2. Identify the separate pieces of the integral (including dx) that you need to express in terms of .

In this case, the function contains two separate pieces that contain x:

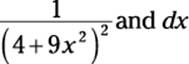
3. Express these pieces in terms of trig functions of .

In the tangent case, all trig functions should be initially expressed as tangents and secants.

To represent the rational portion as a trig function of θ, build a fraction using the radical as the numerator and the constant 2 as the denominator. Then set this fraction equal to the appropriate trig function:

Because this fraction is the hypotenuse of the triangle over the adjacent side , it’s equal to sec θ. Now use algebra and trig identities to tweak

this equation into shape:

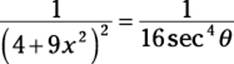
Next, express dx as a trig function of θ. To do so, build another fraction with the variable 3x in the numerator and the constant 2 in the denominator:

This time, the fraction is the opposite side of the triangle over the adjacent side , so it equals tan θ. Now solve for x and then differentiate:

4. Express the integral in terms of and evaluate it:

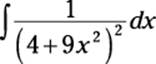
Now some cancellation and reorganization turns this nasty-looking integral into something manageable:

At this point, use your skills from the earlier section “Even powers of sines and cosines” to evaluate this integral:

5. Change the two terms back into x terms:

You need to find a way to express θ in terms of x. Here’s the simplest way:

So here’s a substitution that gives you an answer:

This answer is valid, but most professors won’t be crazy about that ugly second term, with the sine of an arctangent. To simplify it, apply the double-angle sine formula (see Chapter 2) to :

Now use your trig substitution triangle to substitute values for sin θ and cos θ in terms of x:

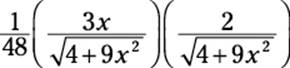
Finally, use this result to express the answer in terms of x:

The secant case

When the function that you’re integrating includes a term of the form (bx² – a²)ⁿ, draw your trig substitution triangle for the secant case. For example, suppose that you want to evaluate this integral:

This is a secant case, because a multiple of x² minus a constant is being raised to a power . Integrate using trig substitution as follows:

1. Draw the trig substitution triangle for the secant case.

Figure 7-3 shows you how to fill in the triangle for the secant case. Notice that the radical goes on the opposite side of the triangle. Then, to fill in the other two sides of the triangle, use the square roots of the two terms inside the radical — that is, 1 and 4x. Place the constant 1 on the adjacent side and the variable 4x on the hypotenuse.

You can check to make sure that this placement is correct by using the Pythagorean theorem: .

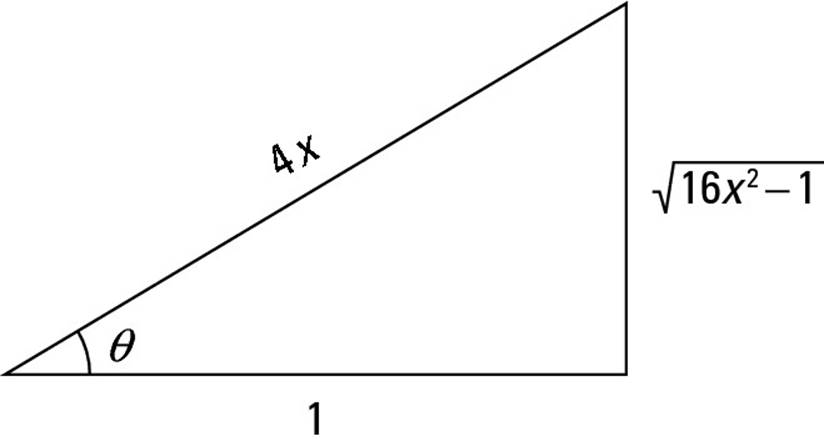
2. Identify the separate pieces of the integral (including dx) that you need to express in terms of .

In this case, the function contains two separate pieces that contain x:

3. Express these pieces in terms of trig functions of .

In the secant case (as in the tangent case), all trig functions should be initially represented as tangents and secants.

To represent the radical portion as a trig function of θ, build a fraction by using the radical as the numerator and the constant 1 as the denominator. Then set this fraction equal to the appropriate trig function:

Notice that this fraction is the opposite side of the triangle over the adjacent side , so it equals tan θ. Simplifying it a bit gives you this equation:

Next, express dx as a trig function of θ. To do so, build another fraction with the variable x in the numerator and the constant 1 in the denominator:

This time, the fraction is the hypotenuse over the adjacent side of the triangle , which equals sec θ. Now solve for x and differentiate to find dx:

4. Express the integral in terms of and evaluate it:

Now use the formula for the integral of the secant function from “Integrating the Six Trig Functions” earlier in this chapter:

5. Change the two terms back into x terms:

In this case, you don’t have to find the value of θ because you already know the values of sec θ and tan θ in terms of x from Step 3. So substitute these two values to get your final answer:

Knowing when to avoid trig substitution

Now that you know how to use trig substitution, I give you a skill that can be even more valuable: avoiding trig substitution when you don’t need it. For example, look at the following integral:

This may look like a good place to use trig substitution, but it’s an even better place to use a little algebra to expand the problem into a polynomial:

Similarly, look at this integral:

You can use trig substitution to evaluate this integral if you want to. (You can also walk to the top of the Empire State Building instead of taking the elevator if that tickles your fancy.) However, the presence of that little x in the numerator should tip you off that variable substitution will work just as well (flip to Chapter 5 for more on variable substitution):

Let u = x² – 49

du = 2x dx

Using this substitution results in the following integral:

Done! I probably don’t need to tell you how much time and aggravation you can save by working smarter rather than harder. So I won’t!