Calculus For Dummies, 2nd Edition (2014)
Part I. An Overview of Calculus
Chapter 3. Why Calculus Works
IN THIS CHAPTER
Using limits to zoom in on curves
Slope equals rise over run
Area of a triangle equals one-half base times height
The Pythagorean theorem: ![]()
In Chapters 1 and 2, I talk a lot about the process of zooming in on a curve till it looks straight. The mathematics of calculus works because of this basic nature of curves — that they’re locally straight — in other words, curves are straight at the microscopic level. The earth is round, but to us it looks flat because we’re sort of at the microscopic level when compared to the size of the earth. Calculus works because after you zoom in and curves look straight, you can use regular algebra and geometry with them. The zooming-in process is achieved through the mathematics of limits.
The Limit Concept: A Mathematical Microscope
The mathematics of limits is the microscope that zooms in on a curve. Here’s how a limit works. Say you want the exact slope or steepness of the parabola ![]() at the point (1, 1). See Figure 3-1.
at the point (1, 1). See Figure 3-1.
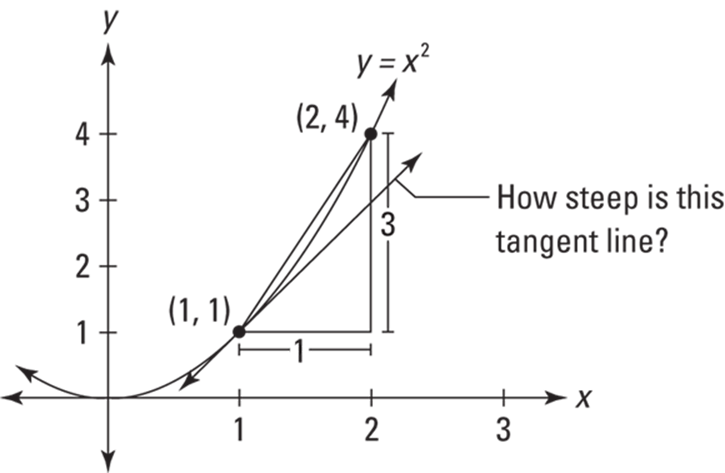
FIGURE 3-1: The parabola ![]() with a tangent line at (1, 1).
with a tangent line at (1, 1).
With the slope formula from algebra, you can figure the slope of the line between (1, 1) and (2, 4). From (1, 1) to (2, 4), you go over 1 and up 3, so the slope is ![]() , or just 3. But you can see in Figure 3-1 that this line is steeper than the tangent line at (1, 1) that shows the parabola’s steepness at that specific point. The limit process sort of lets you slide the point that starts at (2, 4) down toward (1, 1) till it’s a thousandth of an inch away, then a millionth, then a billionth, and so on down to the microscopic level. If you do the math, the slopes between (1, 1) and your moving point would look something like 2.8, then 2.6, then 2.4, and so on, and then, once you get to a thousandth of an inch away, 2.001, 2.000001, 2.000000001, and so on. And with the almost magical mathematics of limits, you can conclude that the slope at (1, 1) is precisely 2, even though the sliding point never reaches (1, 1). (If it did, you’d only have one point left and you need two separate points to use the slope formula.) The mathematics of limits is all based on this zooming-in process, and it works, again, because the further you zoom in, the straighter the curve gets.
, or just 3. But you can see in Figure 3-1 that this line is steeper than the tangent line at (1, 1) that shows the parabola’s steepness at that specific point. The limit process sort of lets you slide the point that starts at (2, 4) down toward (1, 1) till it’s a thousandth of an inch away, then a millionth, then a billionth, and so on down to the microscopic level. If you do the math, the slopes between (1, 1) and your moving point would look something like 2.8, then 2.6, then 2.4, and so on, and then, once you get to a thousandth of an inch away, 2.001, 2.000001, 2.000000001, and so on. And with the almost magical mathematics of limits, you can conclude that the slope at (1, 1) is precisely 2, even though the sliding point never reaches (1, 1). (If it did, you’d only have one point left and you need two separate points to use the slope formula.) The mathematics of limits is all based on this zooming-in process, and it works, again, because the further you zoom in, the straighter the curve gets.
What Happens When You Zoom In
Figure 3-2 shows three diagrams of one curve and three things you might like to know about the curve: 1) the exact slope or steepness at point C, 2) the area under the curve between A and B, and 3) the exact length of the curve from A to B. You can’t answer these questions with regular algebra or geometry formulas because the regular formulas for slope, area, and length work for straight lines (and simple curves like circles), but not for weird curves like this one.
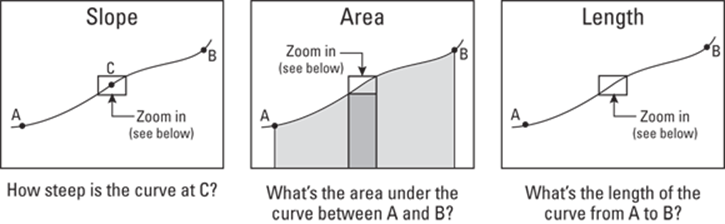
FIGURE 3-2: One curve — three questions.
The first row of Figure 3-3 shows a magnified detail from the three diagrams of the curve in Figure 3-2. The second row shows further magnification, and the third row yet another magnification. For each little window that gets blown up (like from the first to the second row of Figure 3-3), I’ve drawn in a new dotted diagonal line to help you see how with each magnification, the blown up pieces of the curves get straighter and straighter. This process is continued indefinitely.
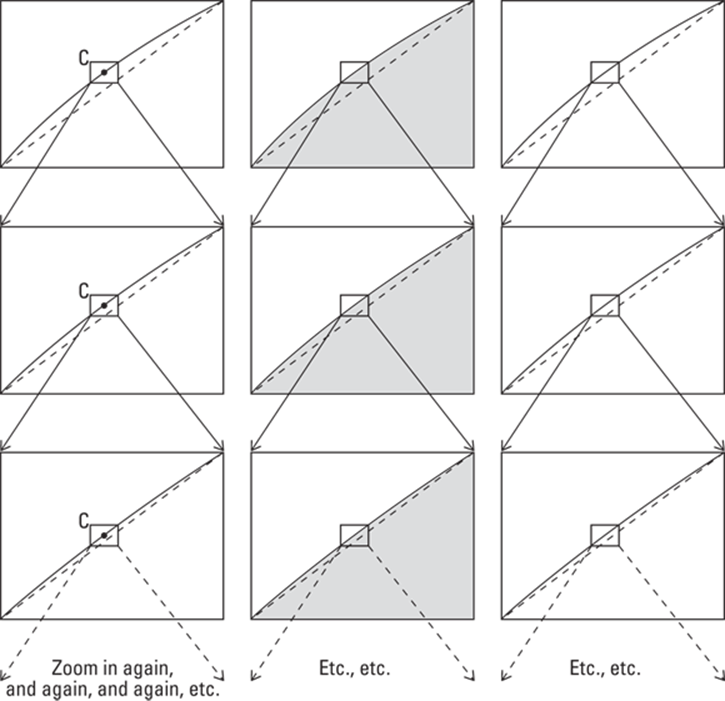
FIGURE 3-3: Zooming in to the microscopic level.
Finally, Figure 3-4 shows the result after an “infinite” number of magnifications — sort of. After zooming in forever, an infinitely small piece of the original curve and the straight diagonal line are now one and the same. You can think of the lengths 3 and 4 in Figure 3-4 (no pun intended) as 3 and 4 millionths of an inch, no, make that 3 and 4 billionths of an inch, no, trillionths, no, gazillionths, …
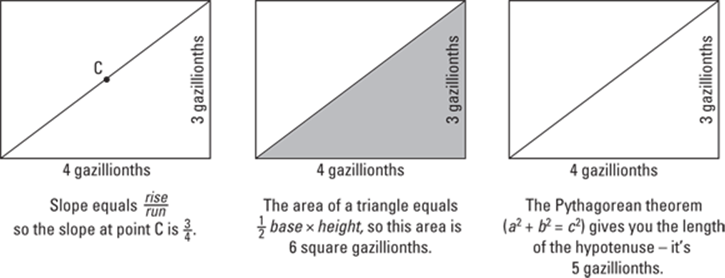
FIGURE 3-4: Your final destination — the sub, sub, sub … subatomic level.
Now that you’ve zoomed in “forever,” the curve is perfectly straight and you can use regular algebra and geometry formulas to answer the three questions about the curve in Figure 3-2.
For the diagram on the left in Figure 3-4, you can now use the regular slope formula from algebra to find the slope at point C. It’s exactly ![]() — that’s the answer to the first question in Figure 3-2. This is how differentiation works.
— that’s the answer to the first question in Figure 3-2. This is how differentiation works.
For the diagram in the middle of Figure 3-4, the regular triangle formula from geometry gives you an area of 6. Then you can get the shaded area inside the strip shown in Figure 3-2 by adding this 6 to the area of the thin rectangle under the triangle (the dark-shaded rectangle in Figure 3-2). Then you repeat this process for all the other narrow strips (not shown), and finally just add up all the little areas. This is how integration works.
And for the diagram on the right of Figure 3-4, the Pythagorean theorem from geometry gives you a length of 5. Then to find the total length of the curve from A to B in Figure 3-2, you do the same thing for the other minute sections of the curve and then add up all the little lengths. This is how you calculate arc length (another integration problem).
Well, there you have it. Calculus uses the limit process to zoom in on a curve till it’s straight. After it’s straight, the rules of regular-old algebra and geometry apply. Calculus thus gives ordinary algebra and geometry the power to handle complicated problems involving changing quantities (which on a graph show up as curves). This explains why calculus has so many practical uses, because if there’s something you can count on — in addition to death and taxes — it’s that things are always changing.
Two Caveats; or, Precision, Preschmidgen
Not everything in this chapter (or this book for that matter) will satisfy the high standards of the Grand Poobah of Precision in Mathematical Writing.
I may lose my license to practice mathematics
With regard to the middle diagrams in Figures 3-2 through 3-4, I’m playing a bit fast and loose with the mathematics. The process of integration — finding the area under a curve — doesn’t exactly work the way I explained. My explanation isn’t really wrong, it’s just a bit sideways. But — I don’t care what anybody says — that’s my story and I’m stickin’ to it. Actually, it’s not a bad way to think about how integration works, and, anyhow, this is only an introductory chapter.
What the heck does “infinity” really mean?
The second caveat is that whenever I talk about infinity — like in the last section where I discussed zooming in an infinite number of times — I do something like put the word “infinity” in quotes or say something like “you sort of zoom in forever.” I do this to cover my butt. Whenever you talk about infinity, you’re always on shaky ground. What would it mean to zoom in forever or an infinite number of times? You can’t do it; you’d never get there. We can imagine — sort of — what it’s like to zoom in forever, but there’s something a bit fishy about the idea — and thus the qualifications.