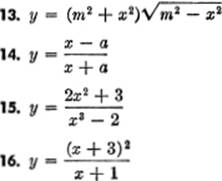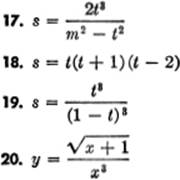The Calculus Primer (2011)
Part III. Differentiation of Algebraic Functions
Chapter 10. DERIVATIVE OF PRODUCTS AND QUOTIENTS
3—6. The Derivative of a Product. Let the function to be differentiated be given by y = uv, where u and v are functions of x. If x is given an increment Δx, the functions u and v, and of course, y, also take on corresponding increments Δu, Δv, and Δy. We then have:
Step 1.y + Δy = (u + Δu) (v + Δv)
= uv + uΔv + vΔu + ΔuΔv.
Step 2.Δy = uΔv + vΔu + ΔuΔv.
Step 3.![]()
Now as Δx → 0, u and v remain unchanged, so that by Principle (II), §1—15, we have
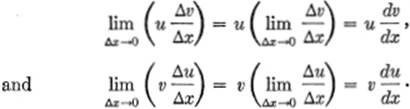
Furthermore, as Δx → 0, Δu and Δv both approach zero; hence
![]()
Step 4.![]()
or![]()
RULE. The derivative of the product of two functions is equal to the product of the first function and the derivative of the second, plus the product of the second function and the derivative of the first.
NOTE. In Step 3, when dividing the product Δu · Δv by Δx, we arbitrarily wrote Δu![]() ; we could just as well have written Δv
; we could just as well have written Δv![]() instead. Since Δv also approaches zero as Δx → 0, the product Δv
instead. Since Δv also approaches zero as Δx → 0, the product Δv![]() vanishes when we pass to the limit, and the final result is the same.
vanishes when we pass to the limit, and the final result is the same.
EXAMPLE 1.Find the derivative: y = 5x4(x3 − 2x).
Solution.Let u = 5x4, and v = x3 − 2x.
Then![]()
![]() = (5x4)(3x2 − 2) + (x3 − 2x)(20x3).
= (5x4)(3x2 − 2) + (x3 − 2x)(20x3).
EXAMPLE 2.Differentiate y = (3x2 + 4) (3x3 − 5x).
Solution.Here u = 3x2 + 4, v = 3x3 − 5x.
Hence ![]() = (3x2 + 4)(9x2 − 5) + (3x3 − 5x)(6x).
= (3x2 + 4)(9x2 − 5) + (3x3 − 5x)(6x).
EXAMPLE 3.Differentiate y = (x2 − 2)![]()
Solution.u = x2 − 2, v = (3x2 + 5)½.
Hence ![]() = (x2 − 2)(
= (x2 − 2)(![]() )(3x2 + 5)−½ · (6x) + (3x2 + 5)½(2x),
)(3x2 + 5)−½ · (6x) + (3x2 + 5)½(2x),
or![]()
EXAMPLE 4.Prove that
![]()
Solution.Let uv = z.
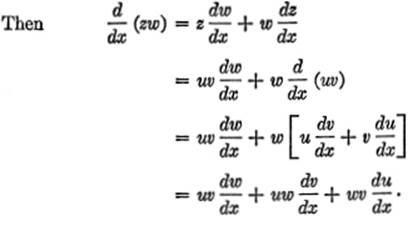
The method of solving Example 4 may be extended to find the derivative of the product of any finite number of functions.
EXERCISE 3—2
Differentiate:
1. y = (x + 1)(x − 2)
2. y = (x2 + 1)(3x + 4)
3. y = (x2 − 1)(2x2 − 3x + l)
4. y = (x3 − 1)2
5. y = (x2 + 1)3
6. y = t(t − 1) (t2 + 2)
7. y = (3x2 + 2x)(4x2 − x)
8. y = (x + 1)(x + 2)(x − 3)
9. y = (t2 − 3t + 4)3
10. y = (x + 2)2 (x + 3)3
3—7. The Derivative of a Quotient. We have already seen in §3—4, [4a] that
![]()
We have also seen (§3—5, NOTE 3) that
![]()
We shall now derive the formula for the derivative of a quotient when both the numerator and the denominator contain variables.
Let y = ![]() . Then, applying the General Rule once again:
. Then, applying the General Rule once again:
Step 1.![]()
Step 2.![]()
Step 3.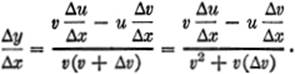
Now as Δx → 0, Δu → 0, and Δv → 0;

RULE. The derivative of a fraction (i.e., a quotient) is equal to the denominator multiplied by the derivative of the numerator, minus the numerator multiplied by the derivative of the denominator, all divided by the square of the denominator.
EXAMPLE 1.Differentiate y = ![]()
Solution.Here u = 2x, and v = x2 + 1.
From equation [7]:

EXAMPLE 2.Differentiate y = ![]()
Solution.u = x + 3, and v = x − 2.
Therefore
![]()
EXAMPLE 3.Differentiate y = ![]()
Solution.u = x2 − x + 2; v = x2 + 3.
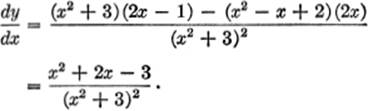
EXERCISE 3—3
Differentiate:
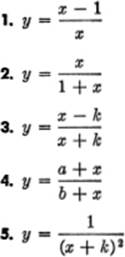

3—8. Importance of Rapid, Accurate Differentiation. It need hardly be pointed out that to use the calculus skillfully requires considerable practice with standard formulas for differentiating various functions. Among the most commonly used formulas are those for the power function, for a product, and for a quotient. The exercise below affords further practice in the use of these formulas.
For the reader’s convenience, we summarize below the standard formulas for differentiating algebraic functions.
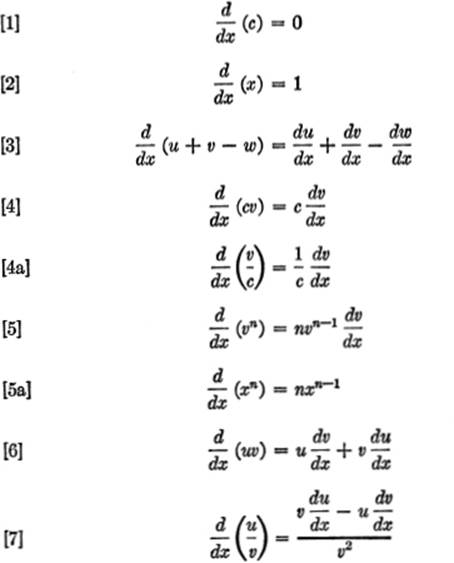
EXERCISE 3—4
Differentiate:
1. y = (x + 3)(x2 − 2)
2. y = (a + x)(b − x)
3. y = x(k + x)2
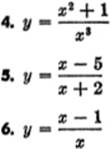
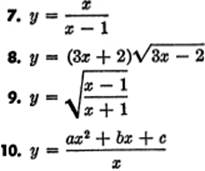
![]()