DIFFERENTIATION OF IMPLICIT FUNCTIONS - Differentiation of Algebraic Functions - The Calculus Primer

The Calculus Primer (2011)

Part III. Differentiation of Algebraic Functions

Chapter 11. DIFFERENTIATION OF IMPLICIT FUNCTIONS

3—9. Explicit and Implicit Functions. Consider the function y2 = 2px. When solved for y, we have y = images or f(x) = images where y = f(x). When solved for x, we have x = y2/2p, where x = ϕ(y). The functions y = f(x) and x = ϕ(y) are explicit functions. In the first instance, y is expressed as a function of x; in the latter case, x is expressed as a function of y. Each function is the inverse of the other. But in the original form y2 = 2px, each variable is defined implicitly as a function of the other. Additional examples of implicit functions are given herewith:

x2 + y2 + 2 = 0;

x2 + xy + y2 = 1;

x3 + y3 = kxy;

x + y = images

Implicit functions, instead of being given as y = f(x), or x = ϕ(y), or s = f(t), are often written as F(x,y) = 0. It may be possible to solve an implicit function F(x,y) = 0 for one of the variables in terms of the other, yielding an explicit function such as y = f(x); sometimes this cannot be done conveniently, and sometimes not at all.

3—10. Differentiation of Implicit Functions. Although it is not always simple or possible to obtain an explicit function from a given implicit function, nevertheless the derivative images can be found, as shown by the following examples.

EXAMPLE 1.Find images in the equation x2 + y2 = 25.

Solution.Differentiate each side of the equation with respect to x:

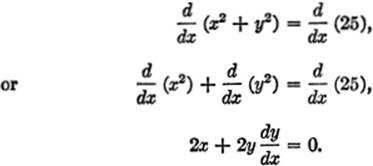
images

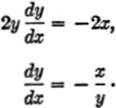
Solve for images:

images

EXAMPLE 2.Find images in the equation y2 = x3.

Solution.Differentiating each side:

2yimages = 3x2.

Solving for images:images

EXAMPLE 3.Find images in the equation xy = a2.

Solution.

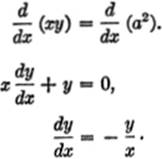
images

EXAMPLE 4.Find images in the equation x2 + y2 − 2xy = 0.

Solution.2x + 2yimages − 2ximages − 2y = 0.

images (2y − 2x) = 2y − 2x,

images = 1.

EXAMPLE 5.Find images in the equation x3 − 2x2y + 2y3 = 0.

Solution.3x2 − 2x2images − 4xy + 6y2images = 0.

images (6y2 − 2x2) = 4xy − 3x2,

images

It should be observed that, in general, as in all the above examples except Example 4, the value obtained for images contains both x and y. If we wish to obtain an expression for the derivative containing only x-terms, we may theoretically replace y by its value in terms of x as found from the original equation, F(x,y) = 0; however, this is sometimes very inconvenient, and is usually not necessary.

It is also worth noting that for most implicit functions, it is generally more convenient to find images by the method shown above than it is first to express the given function explicitly and then to differentiate directly.

EXERCISE 3—3

Find images for each of the following, leaving the remit in terms of x and y:

1. x2 + y2 = 36

2. x2 = 4py

3. xy = − 12

4. x2 − y2 + x − y = 0

5. x2 + y2 + xy = 0

6. 2x + y = images

7. x3(x + a) = y2

8. x + y = 2xy

9. b2x2 + a2y2 = a2b2

10. b2x2 − a2y2 = 1

11. xy2 = 3(x + 2)

12. x2 − y2 + xy + 2y = 4

13. x − y + images = k

14. images

15. x3 + y3 = 3axy

16. x3 + 2x2y + 3y3 = 0

EXERCISE 3—6

Review

Differentiate:

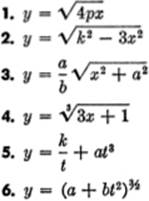
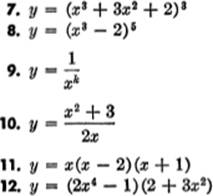
images

images

Find images for each of the following:

13. x2 + y2 + 2x − 4y = 0

14. x3 − xy + y2 = 1

15. x2 + y − x2y = 4

16. x4 + x2y2 + y4 = 16

17. a2x2 − b2y2 = a2b2

18. x2y2 = 2(x2 − y2)

19. Ax2 + Cy2 + Dx + Ey = 0

20. x⅔ + y⅔ = a⅔