The Calculus Primer (2011)

Part IV. Using the Derivative

Chapter 12. THE DERIVATIVE AS A TOOL

4—1. Interpretation of the Derivative. We have already seen that the derivative has several meanings:

(1)As a rate of change in one quantity which varies with another quantity.

If = the average rate of increase (grams per degree, square feet of area per foot of length, etc.),

then = the instantaneous rate of change.

(2)As a time rate of change.

If = the average speed during an arbitrary interval of time Δt,

then = the instantaneous speed.

(3)As a slope.

If = the average slope of a curve in an interval Δx,

then = the slope at a specified point on the curve.

Actually, these three meanings are simply various aspects of the same basic idea, namely, that of an instantaneous rate of change as a limiting value. Thus a speed is simply the rate at which the distance traveled is changing per unit of time; the slope of a curve is the rate at which a curve is rising per horizontal unit.

4—2. When Is a Function Increasing, When Decreasing? It is of great practical value to know whether, at some particular value of x, a given function y = f(x) is increasing or decreasing. If we adopt the convention that x is always increasing, then we can see at once from the graph that the curve is rising at any point where its slope is positive, and falling where its slope is negative. In other words:

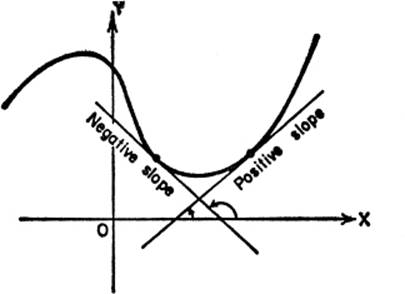
(1)y is increasing when is positive:

(2)y is decreasing when is negative.

The reader should note carefully that it is not a safe test to compare the value of y at the specified point with some near-by value of y; for y might be decreasing at the point in question, but might have increased before reaching this point.