The Calculus Primer (2011)
Part IV. Using the Derivative
Chapter 14. DISTANCE, VELOCITY, AND ACCELERATION
4—4. Distance and Speed. The distance traveled by a moving object is its displacement If this displacement is achieved by motion in a straight line from its original position to a final position, it is referred to as rectilinear motion. The speed with which an object moves is the time rate of change—how far in a given unit of time. If in addition to the numerical value of the time rate of change the direction of motion is also specified, the rate is called the velocity. Thus, a plane flies with a speed of 150 miles per hour, but with a velocity of 150 miles per hour northeast.
If the distance is designated by s, the speed by v, and the time by t, then clearly, from our definitions,
or speed (velocity) equals the derivative of the distance with respect to the time. It is understood, of course, that the motion of a body may be uniform or non-uniform. In general, s is a function of t, or s = f(t).
If the motion is uniform, 
= k, or s = kt; and 
= k. This is the familiar R = 
formula of elementary algebra, where R equals the rate, or .
EXAMPLE 1.An object moves according to the formula s = 30t + 5t2. Find (a) the distance traveled in 4 sec; (b) the distance traveled in the fourth second; (c) its velocity at the end of the fourth second.
Solution.
(a)When t = 4, s = (30)(4) + 5(4)2 = 200 ft.
(b)When t = 3, s = (30)(3) + 5(3)2 = 135 ft.
Hence, during fourth second, the distance covered equals 200 − 135 = 65 ft.
(c)Velocity = = 30 + 10t;
when t = 4, = 30 + 10(4) = 70 ft./sec.
EXAMPLE 2.A missile thrown vertically upward is moving in such a way that the height after t seconds is given by h = 192t − 16t2. Find (a) the velocity at the end of 5 sec; (b) the velocity at the end of 8 sec; (c) the velocity at the end of 6 sec; (d) what is the maximum height reached?
Solution.
h = 192t − 16t2.
= 192 − 35t.
(a)When t = 5, = 192 − (32)(5) = 32 ft./sec.
(b)When t = 8, = 192 − (32) (8) = −64 ft./sec;
the fact that the velocity is negative means that the missile is now moving downward, or falling.
(c)When t = 6, = 192 − (32)(6) = 0;
this means that the missile is moving neither upward nor downward.
(d)The maximum height is attained when = 0, or at t = 6; at t = 6, h = (192)(6) − 16(6)2 = 576 ft.
4—5. Velocity and Acceleration. In motion that is not uniform, the velocity is either increasing or decreasing. The rate at which the velocity is changing is called acceleration; when the velocity is decreasing, that is, when the acceleration is negative, it is frequently called deceleration.
Since acceleration, usually denoted by a, is the rate of change of velocity, we may write
but since velocity is the rate of change of distance, or
we have
The symbol 
is called the second derivative of the function s = f(t). It should not be confused with 
which is the square of the derivative. A second derivative is thus the derivative of a derivative. This is to be expected, since it is the rate at which another rate is changing; or, the rate of change of a rate of change.
EXAMPLE.A body is moving according to the formula s = t3 + 4t2. Find the distance traveled, the velocity, and the acceleration at the instant when t = 3.
Solution.
(a)s = t3 + 4t2,
s3= (3)3 + 4(3)2 = 63ft.
(b)v = 
= 3t2 + 8t,
v3 = 3(3)2 + 8(3) = 51 ft./sec.
(c)a = 
= 6t + 8,
a3 = 6(3) + 8 = 26 ft./sec./sec.
4—6. Laws of a Falling Body. It can be shown from physics that a body when falling freely from rest near the earth’s surface, if air resistance is disregarded, follows the law
s = 
gt2,(1)
where g is the constant of “gravitational acceleration,” and equals about 32.2 feet per second per second when s is measured in feet and t is measured in seconds. From equation (1) we get:
orv = gt;(2)
anda = 
(v) = (gt) = g,
ora = g.(3)
Also, from (1):s = gt2 = t(gt);
but from (2):gt = v;
hences = tv,or2s = vt;
multiplying this last equation by the equation gt = v:
2sgt = v2t
orv2 = 2gs.(4)
Equations (1), (2), and (4) are often referred to as the laws of a freely-falling body.
EXAMPLE.If a body falls freely from rest, find (a) its velocity at the end of 5 sec.; (b) the distance fallen in 10 sec.; (c) its velocity after it has fallen 40 feet.
Solution.
(a)From (2), v = gt = (32.2)(5) = 161 ft./sec.
(b)From (1), s = gt2 = (32.2)(100) = 1610ft.
(c)From (4), v2 = 2gs,
orv = 
= 50.8ft./sec.
4—7. Successive Derivatives. Differentiation may be repeated more than once. Thus, 
, or f″ (x), is the derivative of the derivative of y = f(x); that is,
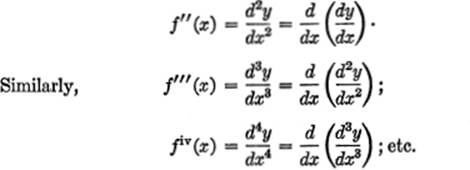
EXAMPLE 1.Find the fourth derivative of y = 2x5 + 3x4 − 10x2 + 5.
Solution.
= 10x4 + 12x3 − 20x;
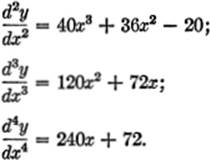
EXAMPLE 2.Find the third derivative of y = 
Solution.y = 3x−5.
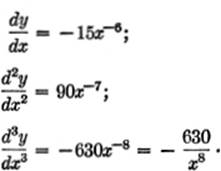
EXAMPLE 3.Find the second derivative of y = 
.
Solution.
EXERCISE 4—2
1. Find the second derivative of each of the following:
(a) y = x5 + 3x3 − 4x
(b) s = 50t2 − 2t5
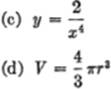
2. Find the third derivative of
(b) z = t(10 − t2)
3. Find the fourth derivative of
(a) y = x6 + 20 + 
(b) s = t5 − t2
4. Given the following equations of rectilinear motion, find the distance, velocity, and acceleration at the instant indicated in each case:
(a) s = 3t + t3, t = 2
(b) s = 10t − 5t2, t = 1
(c) s = 2t3 − 6t2, t = 1
5. An object falls from rest; using the laws of a falling body (§4—6), find (a) its velocity at the end of 10 sec.; (b) its velocity after it has fallen 20 ft.; (c) its acceleration at the instant when t = 6; and (d) the distance it has fallen at the end of 4 seconds. (Use g = 32.2.)
6. If an object starts with an initial velocity of v0 and moves in a straight line with any given constant acceleration a (positive or negative), the distance traveled during a time t elapsed since the beginning of its motion is given by the formula
s = v0t + at2.
Prove: (a) v = v0 + at, and (b) (v2 − v02) = as.
7. Using the formulas from Problem 6, find the acceleration (assumed constant) with which a train, starting from rest, acquires a velocity of 60 miles per hour in 4 minutes. How far does it travel in that time?
8. An automobile moving at 40 miles an hour is brought to rest uniformly in 2 minutes. Find (a) its constant retardation (negative acceleration), and (b) how far it moves in that time.
9. Neglecting air resistance, the height (h ft.) reached in t seconds by an object projected vertically upward with an initial velocity of v0 ft. per sec. is equal to h = v0t − 16.1t2. Find (a) its velocity and acceleration at any instant; (b) its velocity and acceleration at the end of 3 seconds when the initial velocity equals 200 ft. per sec.; and (c) its velocity and acceleration at the end of 12 seconds.
10. A projectile is shot vertically upward with an initial velocity of 1200 ft./sec. Find (a) its velocity at the end of 15 sec.; (b) for how long after it is fired will it continue to rise? (Use formula from Problem 9.)