The Calculus Primer (2011)

Part V. Differentiation of Transcendental Functions

Chapter 16. DERIVATIVES OF LOGARITHMIC FUNCTIONS

5—1. Differentiating a Function of a Function. In this chapter we shall derive standard formulas for differentiating transcendental functions, that is, logarithmic, exponential, and trigonometric functions. Before we can do this, however, we must first discuss the problem of differentiating a function of a function, as well as that of differentiating an inverse function.

It frequently happens that the dependent variable y, instead of being defined directly as a function of x, is given as a function of another variable v, which, in turn, is defined as a function of x. In such a case, y is a function of x through v, and is called a function of a function. For example:

if

and v = 1 + 2x,

then y is a function of a function; that is, y is a function of v, or y = f(v), and v is a function of x, or v = ϕ(x). By eliminating v, we may express y directly as a function of x, or y = F(x). In general, however, this is not convenient, nor is it necessary in order to find .

Let y = f(v), and v = ϕ(x); thus y is a function of x through the function v. If x takes on an increment Δx, then v will take on an increment Δv, and y will take on a corresponding increment Δy. Applying the General Rule to both functions together, we have:

In these last two equations in Step 3, the left-hand members express the ratio of the increment of each function to the increment of the corresponding variable; the right-hand members express the same ratios, respectively, in another form. Before passing to the limit, we may write the product

Step 4. When Δx → 0, both Δy and Δv also approach zero, and we have:

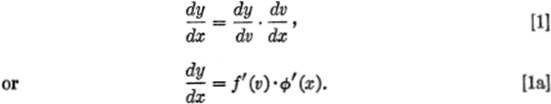
RULE. If y = f(v) and v = ϕ(x), the derivative of y with respect to x is equal to the product of the derivative of y with respect to v and the derivative of v with respect to x.

5—2. Inverse Functions. Consider the pairs of functions given in the two columns below:

It will be noted that each equation in column (A) has been solved for y, while those in column (B) have been solved for x. Thus if y = is called the direct function, as is customary, then x = is the inverse function. In other words, the functions in column (B) are the inverse functions, respectively, of those in column (A). In the direct functions, column (A), y is the dependent variable and x is the independent variable. In the inverse functions, however, y is the independent variable and x is the dependent variable.

5—3. Differentiating an Inverse Function. We shall now proceed to differentiate the inverse functions y = f(x) and x = ϕ(y), together, by the General Rule.

Considering the product of the left-hand expressions, we have:

* The reader should know that the alternative forms arc tan y and tan⁻¹ y are synonymous and interchangeable. In this book we shall consistently use the form arc sin θ for the inverse function of sin θ, arc cos θ for the inverse of cos θ, etc.

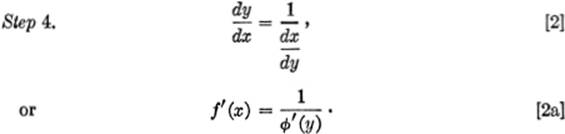
RULE. The derivative of the inverse function is equal to the reciprocal of the derivative of the direct function.

5—4. Logarithmic Functions. Before discussing the derivative of a logarithmic function, a word or two about logarithms may prove helpful. The reader will recall that, by definition,

ifN = a^x,thenx = log_a N.

He will also recall that

log₁₀ N = (log_e N) (log₁₀ e),

where e = 2.718 ... is the base of the natural system of logarithms. It can be shown that log₁₀ e = .434 ... ; this is called the modulus of the system of common logarithms, where the base is 10. More generally, the logarithm of a number N to any base a may be found from the formula where log_a e is the modulus of the particular system whose base is a.

log_a N = log_a e·log_e N = ,

It should be emphasized that in higher mathematics, when we write log v, without designating the base, the base is understood to be e. Hence, since log_e e=1, the modulus of the system of natural logarithms is unity.*

5—5. Differentiation of a Logarithm. We are now in a position to apply the General Rule in deriving a formula for differentiating a logarithm. Consider the direct function

y = log_a v,

where a, the base, is any constant, and v is the independent variable.

Step 1.y + Δy = log_a (v + Δv).

* In advanced mathematics, the notation In x is used to designate log_e x. Thus, In e = 1.

Step 2.Δy = log_a (v + Δv) − log_a v.

By algebra, we have:

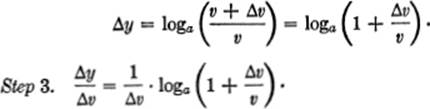
By algebra, we may write this:

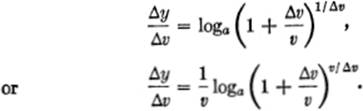
It can be shown that (1 + z)^1/z = e = 2.718.... (See §1—17.)

Now, when Δv → 0, → 0. Hence,

which is clear if we let = z in the expression (1 + z)^1/z.

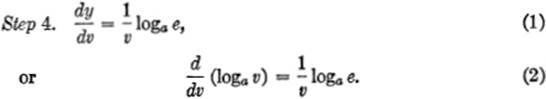
NOTE 1. It should be remembered that the function y = log_av is defined only for positive values of a and v.

NOTE 2. The algebraic transformation made after taking Step 2 and before taking Step 3 is necessary to avoid the occurrence of the indeterminate quotient later when passing to the limit in Step 4.

Since v is a function of x, and we wish to differentiate log v with respect to x, we now make use of §5—1, equation [1], to find the derivative of a function of a function. Since

we may substitute the value of — from equation (1) above in equation (3), giving:

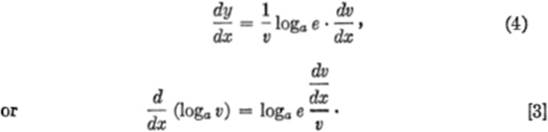
RULE. The derivative of the logarithm of a function is equal to the product of the modulus of the system of logarithms and the derivative of the function, divided by the function.

As a special case, which occurs very often in practice, we note that when a = e, log_a e = log_e e = 1, and formula [3] becomes

EXAMPLE 1.Differentiate y = log x.

Solution.Here v = x.

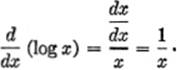
EXAMPLE 2.Differentiate y = log (x³ + a).

Solution.Here v = x³ + a.

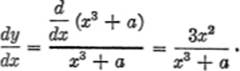
EXAMPLE 3.Differentiate

Solution.Here v = (x² − 2)^½.

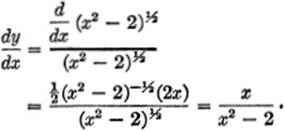
EXAMPLE 4.Differentiate y = log (ax² + bx + c).

Solution.Here v = ax² + bx + c.

EXAMPLE 5.Differentiate

Solution.Here

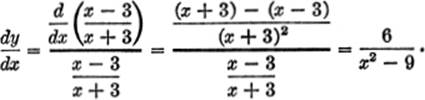
EXAMPLE 6.Differentiate y = log_a (x³ − 4x).

Solution.Here v = x³ − 4x, and the modulus is log_a e; using formula [3] instead of [3a], we obtain:

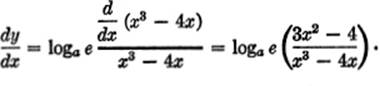
EXERCISE 5—1

Differentiate:

1. y = log (k + x)

2. y = log (x²)

3. y = (log x)²

4. y = log (ax²)

5. y = log (ax + b)

6. y = log (x³ + kx²)

7. y = log (x² + 3x − 2)

8. y = log (ax) + log (2x³)

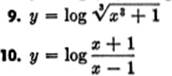
11. y = x log x

12. y = log (x² + ax)

13. y = log x³

14. y = log³ x

17. y = log_a (3x² − 2x)

18. y = log_a (x³ + k)

19. y = x² log x