The Calculus Primer (2011)

Part VI. Further Applications of the Derivative

Chapter 20. SLOPES, TANGENTS, AND NORMALS

6—1.Slope of a Curve. We have seen that for any curve, y = f(x), the slope m of the tangent to the curve at any particular point (x₁,y₁) is given by m = tan ø = , where the symbol indicates the particular value which the variable expression takes when x = x₁ and y = y₁. The reader is urgently cautioned not to think of as meaning the derivative of y₁ with respect to x₁; such an interpretation would be meaningless since both x₁ and y₁ are constants, not variables.

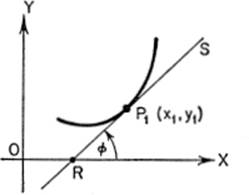
EXAMPLE 1.Find the slope of the tangent to y = x⁴ + 2x³ − 5x + 3 at the point where x = 2.

Solution.

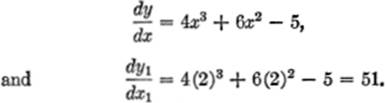
EXAMPLE 2.Find the slope of the tangent to y² = 12x + 13 at the point (3,7).

Solution. Differentiating:

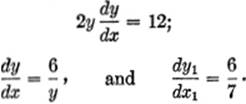
EXAMPLE 3.Find the slope of the curve 2x² + y² = 4x + 42 at the points where x = 3.

Solution. If x₁ = 3, then y₁ = ±6. Differentiating:

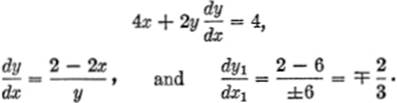
EXAMPLE 4.Find the slope of the curve

x²y² + x³ − 2x − y⁴ − 6y = 0

at the point (0,0).

Solution. Differentiating:

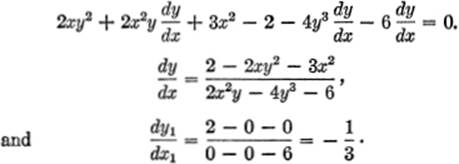
6—2.The Angle between Two Intersecting Curves. The reader will recall that the angle between two intersecting curves is defined as the angle between the tangents to the two curves, respectively, at their point of intersection P(x₁,y₁). Since

it is merely necessary first to determine m₁ and m₂ by differentiation, then to substitute the values of x₁ and y₁ in each of the two derivatives so found, and then to substitute these values in the expression for tan θ.

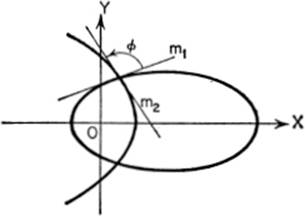
EXAMPLE. Find the angle of intersection between the circle

x² + y² = 25

and the parabola 4y² = 9x.

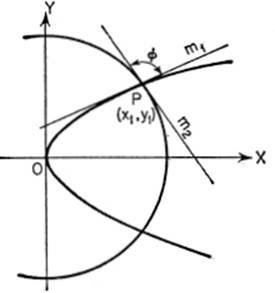
Solution. Solving these equations simultaneously we have:

x = 4, y = ±3.

Letx₁ = 4,y₁ = ±3.

Differentiating:

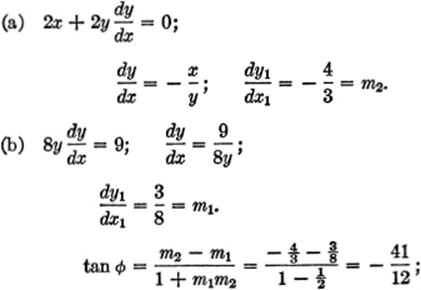
hence, arc tan = arc tan (− 3.417) = 106°20′ (approx.)

EXERCISE 6—1

1. Find the slope of the curve

at any point.

2. Show that the tangent to the circle x² + y² + 2x + 4y = 0 at the origin is parallel to the line x + 2y = 10.

3. Find the slope of the curve

y = x(x³ + 7)⅔

at the point where x = 1.

4. At what point on the curve y² = 3x³ is the slope equal to ?

5. Find the angle of intersection between the curves

x² + y² + 2x − 3 = 0andx² + y² = 7.

6. At what points on the circle x² + y² = k² is the slope of the tangent to the circle equal to – ?

7. Find the angle of intersection of the two parabolas x² = 4py and y² = 4px.

8. Prove that for all values of k, the equation kx = e^v has the same slope, that is, the slope is independent of the value of k.

6—3.Equations of Tangent and Normal. The equation of the tangent, ST, to a curve at a given point P₁(x₁,y₁) is easily derived.

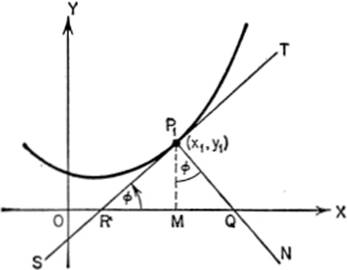
The slope of the tangent in question is given by ; since the point of tangency lies on the tangent as well as on the curve, we may use the point-slope formula for the equation of a line having a given slope and passing through a given point. Thus:

The normal is the line perpendicular to a tangent at the point of contact. Hence the equation of the normal, P₁N, given by

EXAMPLE 1.Find the equations of the tangent and the normal to the curve 4x² + 9y² = 25 at the point where x = 2 and y is positive.

Solution.

At x₁ = 2, y₁ = ±1; taking y₁ positive:

Hence, the equation of the tangent at (2,1) is

y – 1 = – (x – 2),or8x + 9y – 25 = 0

and the equation of the normal at (2,1) is

y – 1 = – (x – 2),or9x + 8y – 10 = 0.

EXAMPLE 2.Find the equations of the tangent and the normal to the equation 2x³ = y² at the point where x = 1 and y is negative.

Solution.

At x₁ = 1, y₁ = ±; taking y₁ negative:

Hence, the equation of the tangent is

The equation of the normal:

6—4.Length of Subtangent and Subnormal. Referring to the diagram in §6—3, the segment RM is called the subtangent of the point P₁; the length of the segment MQ is called the subnormal of P₁. The lengths of these segments, for any curve f(x,y) = 0, can be readily derived.

EXAMPLE 1.Find the lengths of the subtangent and the subnormal to the curve x² = 8y + 4 when x = 6.

At x₁ = 6, y₁ = 4;

EXAMPLE 2.Find the lengths of the subtangent and the subnormal to x² = 2y³ at x = 4.

At x₁ = 4, y₁ = 2; hence,

EXERCISE 6—2

1. Find the length of the subtangent to 3x² − y² = 12 at x = 4.

2. Find the equation of the tangent and the normal to the curve x³ = y + xy at the point where x = − 2.

3. Find the lengths of the subtangent and the subnormal to the curve y² = 4px at any point (x,y).

4. Find the equation of the tangent, and the length of the subtangent, to the circle x² + y² = 25 at x = 3.

5. Find the equation of the tangent to the curve a²(x − y) = x³ + x²y at the origin.

6. Find the length of the subtangent to the curve x = kyⁿ when x = k.

7. Find the length of the subtangent to the curve y = k^x.

8. Prove that the area of the triangle formed by the coordinate axes and any tangent drawn to the curve 2xy = a² is a constant and equal to a².