The Calculus Primer (2011)

Part VI. Further Applications of the Derivative

Chapter 21. POINTS OF INFLECTION AND CURVE TRACING

6—5.Points of Inflection. When a curve changes its nature in such a way that there is a point at which the curve changes from concave downwards to concave upwards, or vice versa, that point is called a point of inflection.

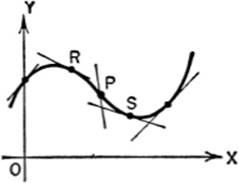
From the discussion of §4—11, it will be seen, from the figure above, that at R, f″(x) is –, and at S, f″(x) is +; for as we move from left to right, or from R to P, the slope, f(x), is decreasing, and when passing from P to S, the slope f′(x) is increasing. Thus, as f″(x) changes from − to + (or + to − ), it must pass through the value zero. Hence:

at a point of inflection, f″(x) = 0.[1]

Points of inflection may also be defined as points where

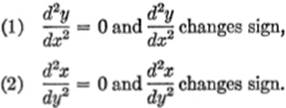
A general principle, given here without proof, is the following:

Given a function f(x) and a specified point x₁ such that f″(x₁) = 0, but f″(x₁) ≠ 0, then x₁ is the abscissa of a point of inflection on the curve y = f(x).

It should be noted that at a point of inflection, the tangent to the curve passes through the curve. Points of inflection are very common. For example, algebraic polynomials of the form

y = a₀xⁿ + a₁xⁿ⁻¹ + a₂x^n-2 + · · · + a_n

in general cannot have more than (n − 2) points of inflection. A parabola cannot have a point of inflection; for if f(x) = ax² + bx + c, then f′(x) = 2ax + b, and f″(x) = 2a; thus there is no value of x which makes f″(x) = 0. Similarly, a straight line can have no point of inflection, since if f(x) = ax + b, then f′(x) = a, f″(x) = 0, and f″′(x) = 0. The trigonometric functions, such as y = sin x, y = cos x, y = tan x, have an infinite number of points of inflection.

EXAMPLE 1.Determine the points of inflection of the curve whose equation is

y = x⁴ − 6x³ + 4x² + 10x − 5,

Solution.

f(x) = x⁴ − 6x³ + 4x² + 10x − 5,

f′(x) = 4x³ − 18x² + 8x + 10,

f″(x) = 12x² − 36x + 8,

f″′(x) = 24x − 36.

The values of x for which f″(x) = 0 are therefore found from the equation

12x² − 36x + 8 = 0;

these values are

EXAMPLE 2.Test for points of inflection the curve of

y = x⁴ − 8x³ + 24x² + 8x.

Solution.

f′(x) = 4x³ − 24x² + 48x + 8,

f″(x) = 12x² − 48x + 48,

f″′(x) = 24x − 48.

Values of x for which f″(x) = 0 are found from the equation

12x² − 48x + 48 = 0,

which gives

(x − 2)² = 0,orx = +2, +2.

However, for the value x = +2,

f″′(x) = 24(2) − 48 = 0;

hence there are no points of inflection, since f″′(x) = 0.

EXAMPLE 3.Find the points of inflection in the curve of y = cos x.

Solution.

f′(x) = − sin x,

f″(x) = − cos x,

f″′(x) = + sin x.

Solving f″(x) = 0 for x:

For these values of x, f″′(x) ≠ 0; hence points of inflection occur at

EXERCISE 6—3

Test the following functions for points of inflection:

1. y = x⁴ + 2x³ − 36x² − x

2. y = x4 + 4x³ + 6x² + 60x

3. y = x⁴ − 12x²

4. y = 2x³

5. y = x⁴

6. y = x5

7. y = e^x

8. y = xe^x

9. y = b + (x − a)³

10. xy − x³ = 1

6—6.Curve Tracing. When discussing curves and equations, an examination of the equation for intercepts, extent, symmetry, and asymptotes constitutes a useful and economical approach to determining the general shape of a curve. For the reader who may have forgotten the tests for symmetry with respect to the origin and the axes, we remind him:

(1) If an equation is unchanged by the substitution of −x for x, the curve is symmetrical with respect to the 7-axis.

(2) If an equation is unchanged by the substitution of −y for y, the curve is symmetrical with respect to the X-axis.

(3) If an equation is unchanged by the substitution of −x for x and −y for y, the curve is symmetrical with respect to the origin.

We also remind the reader who may have forgotten how to determine horizontal and vertical asymptotes:

(1) To find a vertical asymptote, solve the equation for y; if the solution is a fraction, set the denominator equal to zero and solve for x.

(2) To find a horizontal asymptote, solve the equation for x; if the solution is a fraction, set the denominator equal to zero and solve for y.

Limiting our discussion to single-valued functions, we may now add the determination of maximum and minimum values and points of in-flection as further tools for tracing a curve. When all these devices have been used, few additional points need to be calculated and plotted, and it will be possible to sketch the curve fairly accurately with a minimum of preliminary computation.

For convenience, the procedure for curve tracing is outlined below:

Step 1. Find the intercepts on the coordinate axes, if any.

Step 2. Test the curve for symmetry with respect to the axes and the origin.

Step 3. Determine the extent of the curve; that is, what values, if any, of either variable must be excluded.

Step 4. Find the asymptotes, if any, parallel to the coordinate axes; also, how y behaves for numerically (+ or − ) large values of x.

Step 5. Locate the critical points, where f′(x) = 0, and determine all maxima and minima.

Step 6. Locate the points at which f″(x) = 0, and determine all points of inflection.

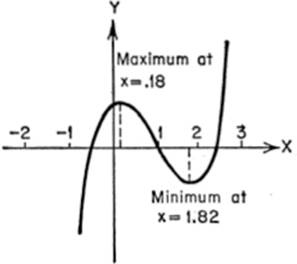
EXAMPLE 1.Trace the curve of y = x³ − 3x² + x + 1.

Solution.

f(x) = x³ − 3x² + x + 1,

f′(x) = 3x² − 6x + 1,

f″(x) = 6x − 6,

f″′(x) = 6.

(1) Intercept on Y-axis = 1. Intercepts on X-axis are and 1, 1 + , and 1 – .

(2) Tests show that the curve is not symmetric to the origin or to either axis.

(3) Inspection shows that no values of x need be excluded.

(4) Inspection shows no asymptotes.

(5) Setting f′(x) equal to zero and solving gives critical values at x = Testing these further, it is found that a minimum exists at x = = 1.82; a maximum exists at x = = +.18.

(6) Setting f″(x) = 0 and solving, x = 1; since f″′(1) ≠ 0, there is a point of inflection at x = 1, i.e., the point (1,0). (That the abscissa of the point of inflection is also a root of f(x) = 0 is entirely accidental and of no significance.)

EXAMPLE 2.Trace the curve of

Solution.

(1)Intercept: x = 0, y = 0.

(2)No symmetry.

(3)Curve not defined when x = 1.

(4)Asymptotes: x − 1 = 0, and y − 1 = 0.

(5) no vaues of x for which f′(x) = 0; hence no maxima or minima.

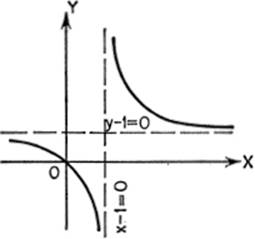
(6)f″(x) = 2(x − 1)⁻³; no values of x for which f″(x) = 0; hence no points of inflection.

EXAMPLE 3.Trace the curve:

y = 2e^−x2

Solution.

(1)When x = 0, y = 2. No value of x makes y = 0. Hence the only intercept is the point (0,2).

(2)Replacing x by −x shows curve symmetric with respect to Y-axis.

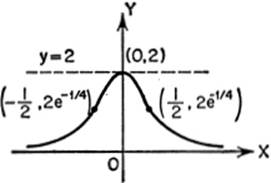
(3)No values of x need be excluded; all values of x yield values of y greater than zero but not greater than 2. Thus the curve lies entirely between the line y = 2 and the X-axis.

(4)As x becomes indefinitely large, positively or negatively, y approaches zero; thus the X-axis is an asymptote.

(5)Differentiating, f′(x) = −4xe⁻²; solving f′(x) = 0 for x, we get x = 0 as the only critical value. As x passes through zero, f′(x) changes from + to −, and so (0,2) is a maximum point.

(6)Setting f″(x) = (16x² − 4)e^−x₂ = 0, we get x = ± Since f″(x) changes sign as x passes through either of these values, the points of inflection are (± ,2e^–1/4).

EXERCISE 6—4

Trace, the following curves and draw the sketch in each case:

1. y = x³ − 9x

2. y = x³ − x² − 5x − 6

5. y = (x − 1)³

6. y = e^2x

7. y = e^−x2

8. y = x(4 − x²)

9. y = x(log x)

10. y = x + sin x

10. Prove that (0,0) is not a point of inflection on the curve y = x⁶ − 2x⁴.

11. Prove that no conic can have a point of inflection.