The Calculus Primer (2011)

Part VI. Further Applications of the Derivative

Chapter 23. RECTILINEAR AND CIRCULAR MOTION

6—8.Component Velocities. Let us consider the path of a curve generated by a moving point following the law y = f(x). The coordinates of x and y of P may be regarded as functions of the time; consequently the motion of y = f(x) may also be defined by means of the parametric equations x = f(t), y = θ(t). If v represents the velocity in the direction of the tangent to the path of y = f(x) at P, then v_x is the horizontal component of the velocity v, and v_y is the vertical component of v.

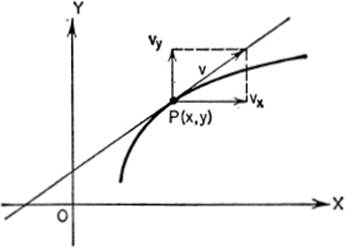
Since by replacing shy x and y, respectively, we have:

= the time rate of change of x,

= the time rate of change of y.

From the figure,

6—9.Component Accelerations. In a similar manner, it is easy to find expressions for the component accelerations. Since v is, in general, a function of the time, v = F(t). If t takes on an increment Δt, then v takes on an increment Δv. Hence the average acceleration during the interval and the acceleration at any instant is the limit of hence,

By reasoning as in §6—8, the component accelerations are readily found to be

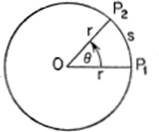
6—10.Circular Motion. Another common type of motion, in addition to rectilinear motion already briefly described, is circular motion. A body moving in a circular pathway may move at a uniform or at a non-uniform rate. If the motion is uniform, the central angle θ changes at a constant rate, known as the angular velocity of the moving point.

If, on the other hand, the motion is non-uniform, say θ = f(t), then the angular velocity will change for various positions of P; its value at any point P is given by The rate of change of the angular velocity for non-uniform circular motion is known as the angular acceleration, and is designated by α. Thus

If s (in feet, inches, etc.) represents the displacement, or distance traveled, as measured algebraically along the circular arc from P₁ to P₂, then

s = rθ,[3]

and the velocity (ft./sec, in./sec., etc.) along the circle is given by

it being understood throughout that θ is measured in radians.

EXAMPLE 1.A motor 4 feet in diameter is revolving uniformly at 2400 revolutions per minute. Find (a) the angular velocity; (b) the velocity of a point on the rim; (c) the distance traveled by a point on the rim in 10 seconds.

Solution.

(a)Angular velocity = ω = 2400 rev. per min.

(b)Velocity of a point on rim = rω = 2(80π) = 160π ft./sec.

(c)Distance traveled by a point on rim in 10 sec. is

(160π)(10) = 1600π ft.

EXAMPLE 2.A point moves on a circle of diameter 24 inches in such a way that its motion follows the law

θ = t³ − 4t² + 6t.

Find (a) the angular velocity at t = 6 sec.; (b) the angular acceleration when t = 2 sec.; (c) the velocity of the point along the circle when t = 4 sec.; (d) the distance along the circle the point has moved when t = 10 sec.

Solution.

(a)
when t = 6, ω = 3(6)² − 8(6) + 6 = 66 radians per sec.

(b)
when t = 2, α = 6(2) − 8 = 4 radians/sec/sec

(c)Velocity along the circle is given by

when t = 4, v = 12(48 − 32 + 6) = 22 inches/sec.

(d)Distance traveled along the circle is given by
s = rθ, where θ = t³ − 4t² + 6t;
when t = 10, θ = 1000 − 400 + 60 = 660 radians; hence s = 12(660) = 7920 inches.

6—11.Circular Motion with Constant Acceleration. If a body moving in a circular path starts from rest with an initial angular velocity of ω₀, so that ω = ω₀ when t = 0 and θ = 0, and if thereafter the motion is constantly accelerated by an amount α, positive or negative, it is shown in physics that throughout the motion the following relations hold:

(1)θ = ω₀t + αt²;

(2)ω = ω₀ + αt;

(3)(ω² − ω₀²) = αθ.

The reader should compare these three equations with the analogous relations for rectilinear motion, given in Exercise 4—2, problem 6.

EXAMPLE 1.A pulley on a shaft is revolving at 120 revolutions per minute. The diameter of the pulley is 3 ft. If the pulley is brought to rest at a constant (uniform) retardation in f minute, find (a) the constant retardation, and (b) the number of revolutions made by the pulley before coming to rest.

Solution.

(a)ω₀ = 120 r.p.m. = 240π radians/min.;
ω = 0, the final velocity.

ω = ω₀ + αt,

0 = 240π + α(),

α = − 320π radians/min./min.

(b)θ = ω₀t + αt²,

90π ÷ 2π = 45 revolutions.

EXAMPLE 2.The armature of an electric motor is revolving at the rate of 1500 r.p.m. It is brought to rest at a uniform retardation of 5 radians per second. Find (a) the time required to bring it to rest; (b) how many revolutions it will make in coming to rest; and (c) how far a point on the rim will travel during this period, if the radius of the armature is 6 inches.

Solution.

(a)ω₀ = 1500 r.p.m. == 25 rev./sec. = 50π radians/sec.
α = −5 radians/sec.

ω = ω₀ + αt,