The Calculus Primer (2011)

Part VIII. Curvature

Chapter 29. LENGTH OF ARC

8—1.Differential Arc Length. In order to understand the nature of curvature, it will be necessary to discuss what is meant by differential arc length. Let the curve in the figure represent the function y = f(x), and let s represent the length of the arc measured from a definite, initial point P₀ to any point P(x,y) of the curve. Since the length s will depend upon the position of P₀ on the curve, s is clearly a function of x. Thus suppose that as x takes on an increment Δx, the corresponding increment of s is Δs, and the corresponding point on the curve is R(x + Δx, y + Δy). Intuitively, from the figure, we note that

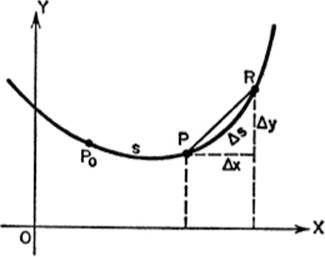
PR² = (Δx)² + (Ay)²,(1)

and hence

Again intuitively, we see that, as Δx approaches zero, arc Δs and chord PR become more and more nearly equal, so that

Let us now transform the left-hand member of (2) by multiplying both numerator and denominator by (Δs)², and rewriting; thus

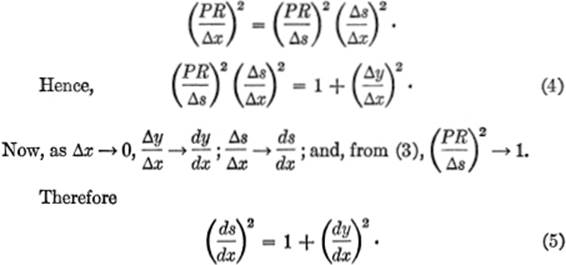
In other words, as s increases with x, we have

In differential notation:

The right-hand member of [1a] is an expression for the differential arc length ds.

It often happens that the given function is of the form x = ø(y), and s is an increasing function of y. In this case the corresponding formulas for differential arc length, by similar reasoning, are found to be

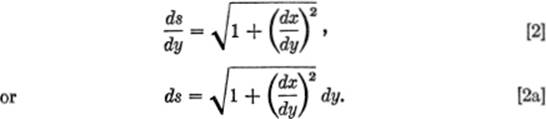
8—2.Differential Arc Length for Equations in Parametric Form. If the function to be considered is given by a set of parametric equations, let us say

x = f(t), y = ø(t)

where t is the parameter, we may proceed as follows.

From equation (5), §8—1,

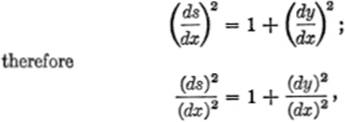
or, clearing of fractions,

(ds)² = (dx)² + (dy)².(1)

Since x = f(t) and y = ø(t),

dx = f′(t) dt, and dy = ø′ (t) dt.(2)

Substituting (2) in (1):

(ds)² = [f′(t) dt]² + [ø′ (t) dt]²,

8—3.Differential Arc Length in Polar Coordinates. If the function whose differential arc length is desired is expressed in polar coordinates, the corresponding formulas are easily derived by employing the usual transformation formulas from rectangular to polar coordinates, namely,

x = ρ cos θ, y = ρ sin θ,(1)

Differentiating (1), using differential notation:

Substituting in [3], §19—2:

(ds)² = (−ρ sin θ dθ + cos θ dρ)² + (ρ cos θ dθ + sin θ dp)².

Simplifying:

(ds)² = ρ² (sin² θ + cos² θ)(dθ)² + (sin² θ + cos² θ) (dp)²,

(ds)² = ρ²(dθ)² + (dp)².[3a]

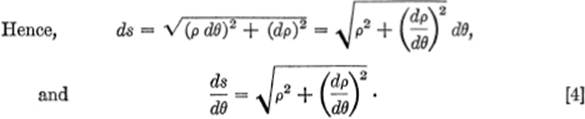
To sum up, the differential length of arc is given by the formulas:

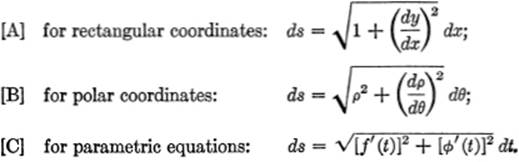
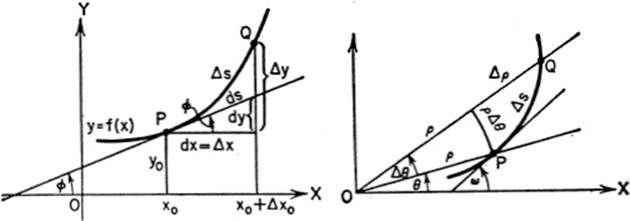
Thus the differentials dx, dy, and ds form the sides of a right triangle in which

(ds)² = (dx)² + (dy)².[5]

Similarly, the differentials dρ, ρ dθ, and ds are related in such a way that they represent a right triangle whose hypotenuse is ds, and whose sides are dρ and ρ dθ; or

(ds)²= (dp)²+(ρdθ)².[6]