The Calculus Primer (2011)
Part XI. Expansion of Functions
Chapter 39. INFINITE SERIES AND SIGMA NOTATION
11—1. Basic Ideas and Notation. The reader is already familiar, from his algebra, with the notion of arithmetic series and geometric series.
(A) ![]()
(B) x, x – 2a, x – 4a, x – 6a, ... .
Thus, (A) is a geometric series (common ratio = –![]() ), while (B) is an arithmetic series (common difference = −2a).
), while (B) is an arithmetic series (common difference = −2a).
Any sequence of n terms in the form
u1 + u2 + u3 + … + un−1 + un,
where the nth term is a given function of n, is called a series. For example:

In series (C), (D), and (E), the general term, or the nth term, is seen to be a function of n. The law of formation in each case, while perhaps not as simply stated as for an arithmetic or a geometric series, is nevertheless just as definite. Although the nth term is the last one expressed, it need not be the “last” term, literally; in fact, the nth term generalizes the law of formation, in accordance with which it is always possible to form a “next” term, no matter how many terms have preceded it. When the number of terms in a series is regarded as endless, we speak of the series as an infinite series. In such a series there is no last term, and the number of terms is said to be infinitely great. An infinite series is represented simply by
u1 + u2 + u3 + … ,
where u1 is the “first” term, and the three dots represent the indefinite continuation of successive terms, all following the same law of formation followed in writing the first three terms.
When only a few (three or four) of the first terms of an infinite series are expressed, it is to be assumed that the general term, or nth term, is that function of n which takes the value of the first term when n = 1, the value of the second term when n = 2, the value of the third term when n = 3, the value of the 10th term when n = 10, etc. For example:
in ![]() , the nth term is
, the nth term is ![]() ;
;
in ![]() , the nth term is
, the nth term is ![]() ;
;
in ![]() , the nth term is
, the nth term is ![]() .
.
11—2. Convergent Series. Consider an infinite series
u1 + u2 + u3 + … , (1)
and suppose that the sum of the first n items is represented by Sn; thus
Sn = u1 + u2 + u3 + u4 … + un,
where n is a finite, or definite number, regardless of how large or small. Now if, as n increases indefinitely, the value of ![]() Sn has a definite, finite value, the series (1) is called a convergent series. In other words, in such a series, the greater the number of terms taken, the closer in value the sum of these terms becomes to some limiting value, or “sum,” namely,
Sn has a definite, finite value, the series (1) is called a convergent series. In other words, in such a series, the greater the number of terms taken, the closer in value the sum of these terms becomes to some limiting value, or “sum,” namely, ![]() Sn.
Sn.
While we speak of this value to which the series converges as a “sum,” it is not a sum in the strict sense of the word, since the number of terms taken, or the number of addends, is indefinite. In reality, the value of Sn is the limit of a series of different sums, each, in turn, successively closer to the numerical value of ![]() Sn. For example, if we take the series
Sn. For example, if we take the series
![]()
we see that it is a geometric series in which a = 3 and r = ![]() ; hence
; hence
![]()
Passing to the limit:
![]()
Therefore, since ![]() Sn has a definite finite value, the series (2) is convergent.
Sn has a definite finite value, the series (2) is convergent.
11—3. Divergent Series. There are some series, however, for which ![]() Sn does not have a definite finite value; such series are called divergent series. The following are examples of divergent series.
Sn does not have a definite finite value; such series are called divergent series. The following are examples of divergent series.
EXAMPLE 1. In the arithmetic series
1 + 5 + 9 + 13 + 17+ ... + (4n−3),
it is clear that as n → ∞, Sn increases without limit, and the series is divergent. In other words, it is always possible to find a value for n such that the value of Sn is greater than any preassigned value.
EXAMPLE 2. Another type of divergent series is
1 − 1 + 1 − 1+ ... + (−1)n−1+ ... ,
which is known as an oscillating series, since the values of Sn oscillate between 0 and 1, according as n is even or odd. The ![]() Sn in such a series is meaningless.
Sn in such a series is meaningless.
EXAMPLE 3. Some series which upon superficial inspection would appear to be convergent are actually divergent. Such a series is the harmonic series.
![]()
Let us group the terms as follows:
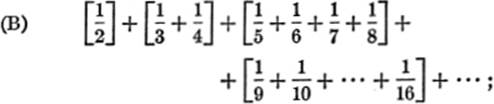
now compare the value of each of these groups with the corresponding group of the series
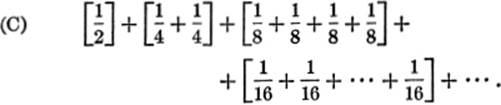
It is easily seen that the value of each group in (B) is greater than the value of the corresponding group in (C); but each group in (C) is equal to ![]() , so that the sum of these groups can be made as large as we please, simply by taking a sufficient number of terms. The same is therefore true of (B); hence (B), and therefore (A), is a divergent series. It should be noted that in the harmonic series, the successive terms approach zero as a limit, and it is difficult, at first sight, to believe that the successive sums of this series add up to a value greater than any number which we can assign.
, so that the sum of these groups can be made as large as we please, simply by taking a sufficient number of terms. The same is therefore true of (B); hence (B), and therefore (A), is a divergent series. It should be noted that in the harmonic series, the successive terms approach zero as a limit, and it is difficult, at first sight, to believe that the successive sums of this series add up to a value greater than any number which we can assign.
11—4. Sigma Notation. We frequently designate an infinite series in the so-called sigma notation by writing
![]() read “summation un,”
read “summation un,”
or ![]() read “summation un from n = 1 to n = ∞.”
read “summation un from n = 1 to n = ∞.”
Thus
![]()
The subscript n is the same as the ordinal number of the term.
Sometimes a series is written as
![]()
in this case the nth term is un−1 the subscript being one less than the number of the term; un becomes the (n + l)st term of the series, and
Sn = u0 + u1 + u2 + … + un−1.
EXERCISE 11—1
Write the first five terms of each of the following series:
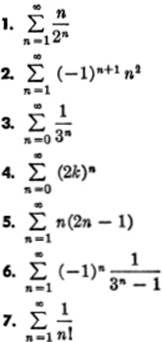
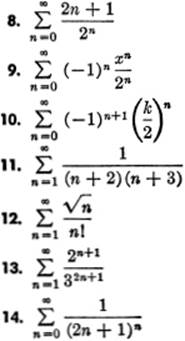
![]()
Write the general, or nth term, for each of the following:

