The Calculus Primer (2011)

Part XI. Expansion of Functions

Chapter 41. POWER SERIES

11—11. Convergence of Power Series. Any series of the form

a₀ + a₁x + a₂x² + a₃x³ + … + a_n−1xⁿ⁻¹ + a_nxⁿ + … ,

where a₀, a₁, a₂, … are constants, is known as a power series in x. Such series are important in higher mathematics, for they are often used in finding the values of a given function. In fact, we shall develop special methods for expressing any ordinary function in terms of a series.

Whether a power series converges or diverges depends upon the particular value assigned to x. Thus every power series converges when x = 0. A power series may converge for all values of x, or for no values of x other than zero. In general, however, a power series converges for some values of x besides x = 0, and diverges for other values of x.

To determine the values for which a power series converges, we use the following ratio test. Thus in a power series, if = L, then the series

(a)converges for all values of x such that |x| < L;

(b)diverges for all values of x such that |x| > L;

(c)no test if |x| = L.

11—12. Interval of Convergence of a Power Series. The values of x for which a power series converges are said to constitute the interval of convergence for the series. It can be proved that this interval, when plotted, will always have zero as the center. A series may or may not converge for the value of x at either end point of its interval of convergence. For all other values of x, the series is divergent.

EXAMPLE 1. Find the values of x for which the series is convergent:

Solution. Here a₀ = 1, a₁ = , a₂ = , etc.

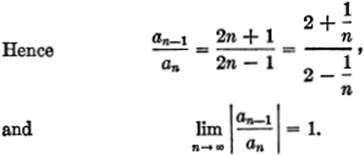
Hence the series converges for |x| < 1, that is, for –1 < x < 1; it diverges for |x| > 1, that is, for –1 > x > 1. To test the end points:

when x = 1, we have

which is divergent;

when x = − 1, we have

which is also divergent.

Hence the end points are not included in the interval of convergence.

EXAMPLE 2. Find the values of x for which the series is convergent:

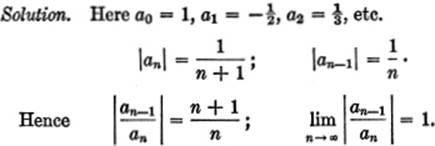
Thus the series converges for |x| < 1, or for − 1 < x < 1.

To test the end points:

when x = 1, we have

which is convergent;

when x = − 1, we have

which is divergent.

Hence for the original power series, the end point x = + 1 is included in the interval of convergence, but the other end point, − 1, is not included.

EXAMPLE 3.Find the interval of convergence of

Solution. Here a₀ = 1, a₁ = 1, a₂ = , etc.

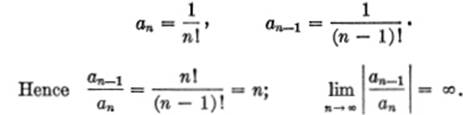
Therefore the series converges for |x| < ∞, that is, for — ∞ < x < ∞, or for all positive and negative values of x.

EXERCISE 11—4

Determine the values of x for which the following series are convergent: