The Calculus Primer (2011)
Part XII. General Methods of Integration
Chapter 46. STANDARD ELEMENTARY INTEGRAL FORMS
12—8. Standard Integrals. Thus far we have discussed five so-called standard elementary integrals, which we restate below for convenience:
![]() dx = x + C [1]
dx = x + C [1]
![]() a dv = a
a dv = a ![]() dv [2]
dv [2]
![]() (du + dv − dw) =
(du + dv − dw) = ![]() du +
du + ![]() dv −
dv − ![]() dw [3]
dw [3]
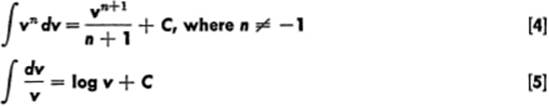
We now give a list of the remaining standard integral forms for reference:

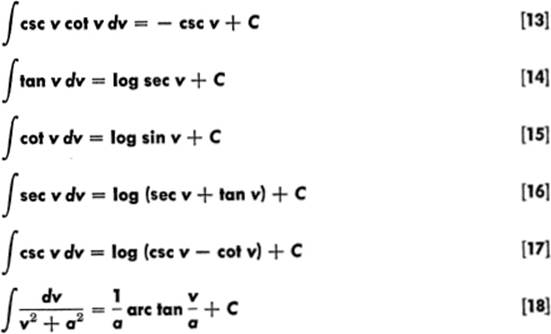
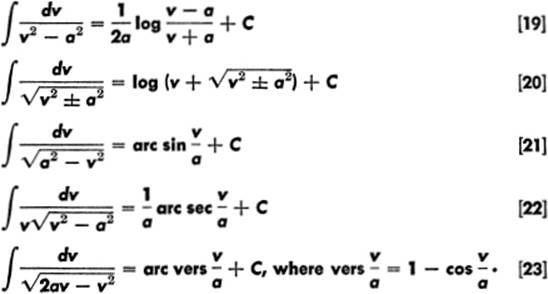
12—9. The Forms ![]() avdv and
avdv and ![]() ev dv. These formulas are seen to be true from the following considerations. We know that
ev dv. These formulas are seen to be true from the following considerations. We know that
d(av) = log a·av·dv;
integrating both sides, we get:
av = ![]() log a·av·dv,
log a·av·dv,
or av = log a ![]() av dv;
av dv;
hence ![]()
In a similar manner, since
d(ev) =evdv,
it follows that ![]() ev dv = ev + C.
ev dv = ev + C.
The reader can readily verify these results by differentiation.
EXAMPLE 1. Find ![]() e2x dx.
e2x dx.
Solution. If we let v = 2x, then dv = 2dx. Now, in order to make the expression ![]() e2x dx conform to the standard form
e2x dx conform to the standard form ![]() ev dv, since dv = 2dx when v = 2x, we insert the factor 2 before the dx, and the factor
ev dv, since dv = 2dx when v = 2x, we insert the factor 2 before the dx, and the factor ![]() before the integral sign; thus
before the integral sign; thus
![]()
but ![]() ev dv = ev + C, hence
ev dv = ev + C, hence ![]()
EXAMPLE 2. Find ![]() 2a3x dx.
2a3x dx.
Solution. Let v = 3x; then dv = 3dx. Insert 3 before the dx, and ![]() before the integral sign; then
before the integral sign; then
![]()
EXAMPLE 3. Find ![]() ecos x (sin x) dx.
ecos x (sin x) dx.
Solution. Let v = cos x; dv = − sin x dx; then
![]() ecos x (sin x dx) =
ecos x (sin x dx) = ![]() ecos x (− sin x dx) = − ecos x + C.
ecos x (− sin x dx) = − ecos x + C.
EXERCISE 12—4
Find the following integrals; check by differentiation:
1. ![]()
![]() e4z dx
e4z dx
2. ![]() kamx dx
kamx dx
3. ![]() esin x (cox x) dx
esin x (cox x) dx
4. ![]() e2 sin x (cos x) dx
e2 sin x (cos x) dx
5. ![]() e−3x dx
e−3x dx
6. ![]() ax/n dx
ax/n dx
7. ![]() a2x−1 dx
a2x−1 dx
8. ![]() e2x3·x2 dx
e2x3·x2 dx
9. ![]() ex (ex + 1)dx
ex (ex + 1)dx
10. ![]()
![]()
11. ![]() xkx2 dx
xkx2 dx
12. ![]() (ex/2 + e−x/2)dx
(ex/2 + e−x/2)dx
12—10. Standard Forms [8] through [13]. These formulas follow immediately from the corresponding formulas for differentiation, as given in §5—9, §5—10, §5—11, §5—12, equations [6]–[11]. They may be verified simply and directly by differentiation.
EXAMPLE 1. Find ![]() cos 3ax dx.
cos 3ax dx.
Solution. Let v = 3ax; then dv = 3a dx.

EXAMPLE 3. Find ![]() csc2x2·x dx.
csc2x2·x dx.
Solution. Let v = x2; then dv = 2x dx.
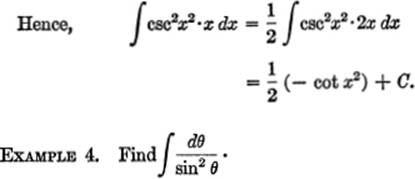
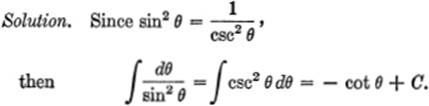
EXERCISE 12—5
Find the following integrals; check by differentiation:
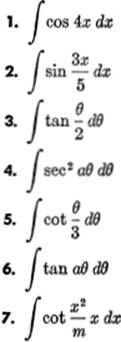
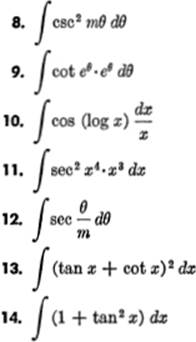
Verify the following:
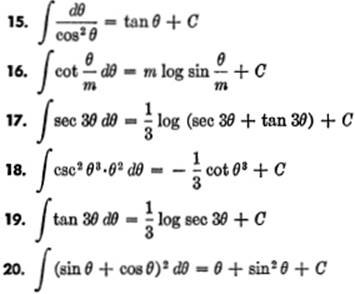
12—11. Standard Forms [14]–[17]. These four formulas may be proved by transforming the integrand in each case so that we may apply equation [5]; the proofs follow.
Form [14]:
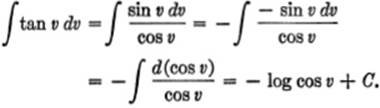
But − log cos v = − ![]() = − log 1 + log sec v = log sec v;
= − log 1 + log sec v = log sec v;
hence, ![]() tan v dv = log sec v.
tan v dv = log sec v.
Form [15]: In a similar manner,
![]()
Form [16]: To transform the integrand so that it will be in the form ![]() we write:
we write:
![]()
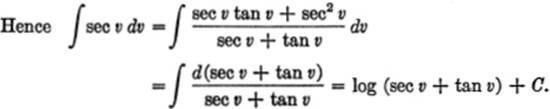
Form [17]: This may be derived in a manner similar to the proof for [16]. We leave it as an exercise for the reader; multiply the integrand csc v by the fraction ![]() .
.
12—12. Forms [18]–[23]. The formulas for the standard forms [18]–[23] may be derived by suitable transformations or substitutions. Formulas [22] and [23] follow at once from the corresponding formulas for differentiation.
EXAMPLE 1. Find ![]()
Solution. Let v2 = 9x2, and a2 = 4; then v = 3x, dv = 3dx, and a = 2.
From formula [18], we get:
![]()
EXAMPLE 2. Find ![]()
Solution. Let v2 = 4x2, and a2 = 25; then v = 2x, dv = 2dx, and a = 5.
From formula [19], we get:
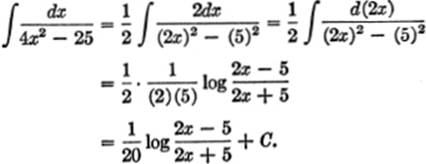
EXAMPLE 3. Find ![]()
Solution. Let v2 = 4x2, and a2 = 9; then v = 2x, dv = d(2x), and a = 3.
From formula [20]:
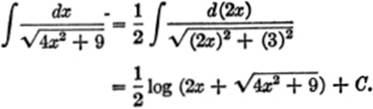
EXAMPLE 4. Find ![]() .
.
Solution. Let v2 = 5x2, and a2 = 3; then v = ![]() x, dv =
x, dv = ![]() dx, and a =
dx, and a = ![]() .
.
From formula [19]:
![]()
EXAMPLE 5. Find ![]()
Solution. Rewrite as follows:
![]()
Here v = 2x, a = 5, dv = 2dx.
From formula [22]:
![]()
EXAMPLE 6. Find ![]()
Solution. Let v2 = x4, and a2 = 36; then v = x2, dv = 2x dx, and a = 6.
From formula [20]:
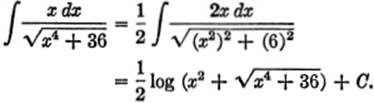
EXAMPLE 7. Find ![]()
Solution. Rewrite as follows, completing the square in the denominator:
![]()
Now apply formula [18], where v = x + 2, a = 4.
![]()
EXERCISE 12—6
Find the following integrals; check by differentiation:
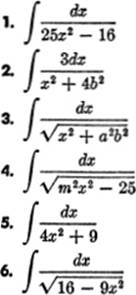
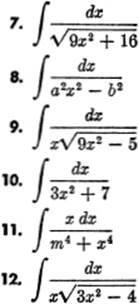
Verify the following:
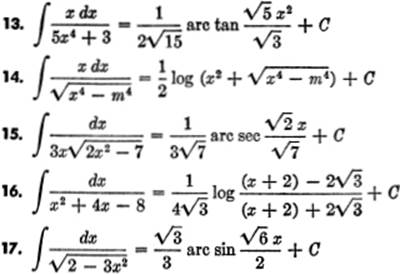
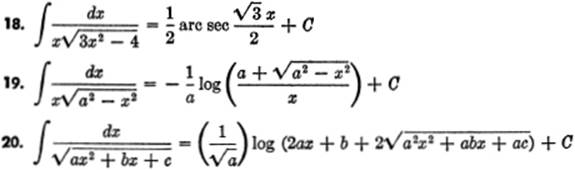
EXERCISE 12—7
Review
Find the following integrals:
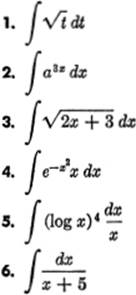
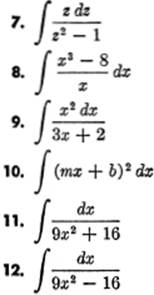
13. ![]() ecos x.sin x dx
ecos x.sin x dx
14. The slope of a certain curve is given by ![]() = 6x2 − 10x + 8. If the curve passes through the point (2,10), find its equation.
= 6x2 − 10x + 8. If the curve passes through the point (2,10), find its equation.
15. If ![]() = 12x + 6, find y in terms of x if it is known that when x = 2,
= 12x + 6, find y in terms of x if it is known that when x = 2, ![]() = 28, and when x = −3, y = − 1.
= 28, and when x = −3, y = − 1.