The Calculus Primer (2011)

Part XIII. Special Methods of Integration

Chapter 48. TRIGONOMETRIC INTEGRALS

13—3. Trigonometric Reduction. Many differentials containing trigonometric functions can be reduced to standard forms for integration by first making appropriate trigonometric transformations.

EXAMPLE 1. Find sin² x dx.

Solution. By trigonometry, sin²

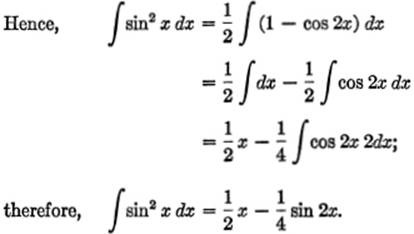
NOTE: This may also be written, by trigonometry, as

since sin 2x = 2 sin x cos x.

EXAMPLE 2. Find sin³ θ dθ.

Solution. By trigonometry,

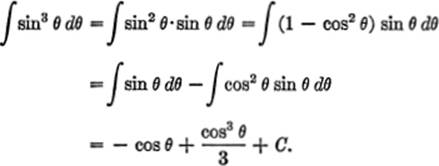
EXAMPLE 3. Find sin⁵ θ cos² θ dθ.

Solution.

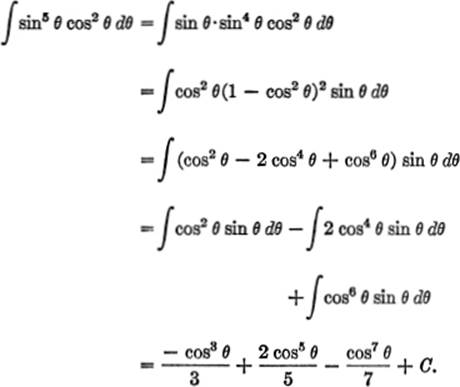
EXAMPLE 4. Find cot⁴ x dx.

Solution.

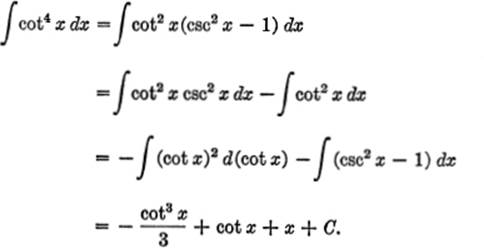
EXAMPLE 5. Find sin² θ cos⁴ θ dθ.

Solution. See §13—4, II, below, for trigonometric substitutions:

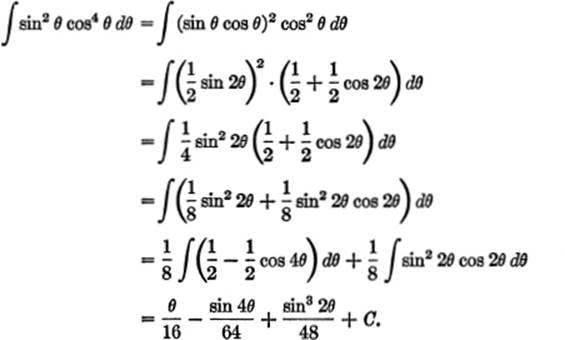
13—4. Summary of Trigonometric Reductions.

I. To find sin^m x cosⁿ x dx, when either m or n is a positive, odd whole number, we transform the expression to be integrated by means of the relation sin² θ = 1 — cos² θ, or cos² θ = 1 — sin² θ, in such a way that we may apply the standard form

II. To find sin^m x cosⁿ x dx, when both m and n are positive even whole numbers, we make use of the trigonometric relations:

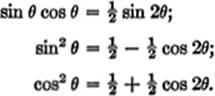
III. To find sin mx cos nx dx, sin mx sin nx dx, or cos mx cos nx dx, we use standard reduction formulas; the proofs of these formulas are not given here, but they are based upon the addition formulas of trigonometry, that is, sin

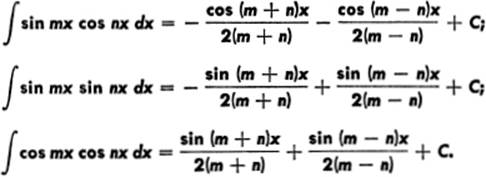
EXERCISE 13—2

Find the following:

1. cos² θ dθ

2. cos³ θ dθ

3. sin⁵ θ dθ

4. cos² θ sin² θ dθ

5. sin⁴ θ dθ

6. cot² θ dθ

7. sin³ θ cos θ dθ

8. sin² θ cos θ dθ

9. cos³ θ sin θ dθ

10. tan³ θ dθ

11. sin³ θ cos² θ dθ

12. (tan 2θ)² dθ