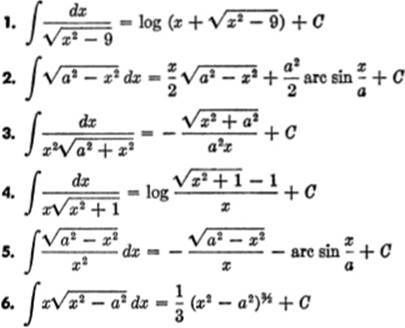The Calculus Primer (2011)

Part XIII. Special Methods of Integration

Chapter 49. INTEGRATION BY SUBSTITUTION; CHANGE OF VARIABLE

13—5. Algebraic Substitution. Frequently an expression to be integrated can be transformed, by the suitable substitution of a new variable, into one of the fundamental standard forms. Some of the simpler kinds of such substitutions will now be illustrated.

EXAMPLE 1. Find

Solution.

Let

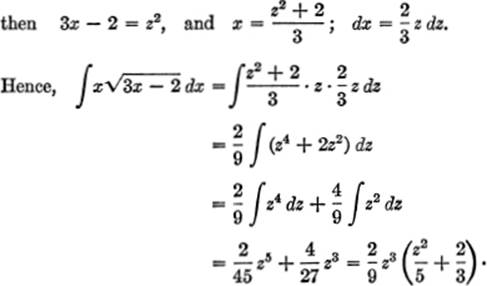
Substituting (3x − 2)^½ for z:

EXAMPLE 2. Find

Solution.

Let z = (3x + l)^⅓;

then dx = z² dz, and (3x + 1)^⅔ = z².

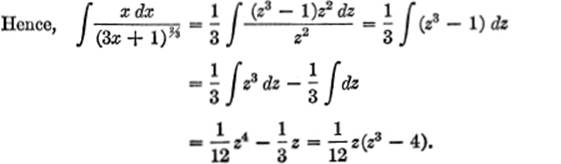
Substituting (3x + 1)^⅓ = z:

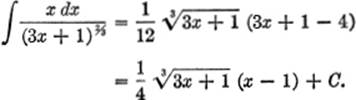
EXAMPLE 3. Find

Solution. Let x = z; then x = z⁶, dx = 6z⁵ dz, x^⅓ = z³, and x^⅓ = z².

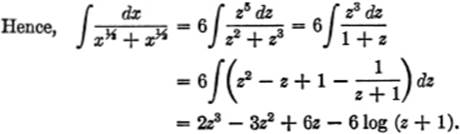
Substituting for z, z², and z³:

EXAMPLE 4. Find

Solution. Let z = ; then x = z² + 3, and dx = 2z dz.

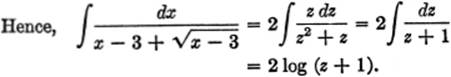
Substituting

EXERCISE 13—3

Find the following:

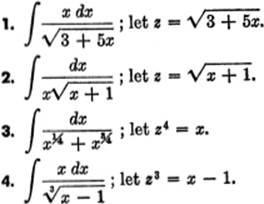
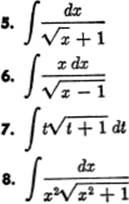
Verify the following:

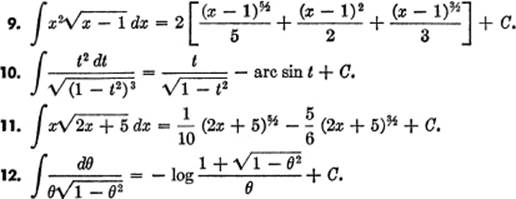
13—6. Trigonometric Substitutions. When the integrand contains expressions such as the integration may be performed by using the following trigonometric substitutions:

I.For we put v = a sin θ; the expression then becomes:

II.For we put v = a tan θ; the expression then becomes:

III.For we put v = a sec θ; the expression then becomes:

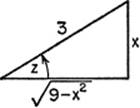
EXAMPLE 1. Find

Solution. Let a² = 9, a = 3; x = 3 sin z, dx = 3 cos z dz; Therefore,

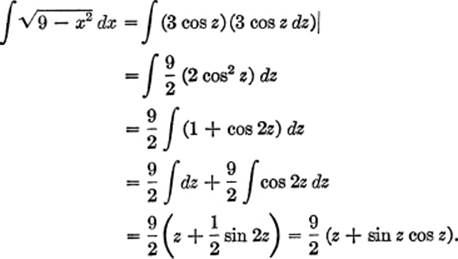
But, x = 3 sin z; from the triangle of reference we have z = arc sin , and cos hence

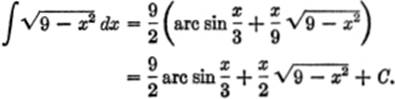
EXAMPLE 2. Find

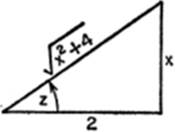
Solution. Let x = 2 tan z; dx = 2 sec² z dz;

= log (sec z + tan z).

Therefore, from the triangle of reference,

EXAMPLE 3. Find

Solution. Let x = a sec z; dx = a sec z tan z dz; = a tan z.

Therefore,

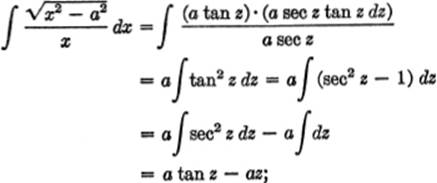
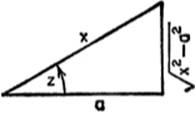
But sec z = ; hence, from the triangle:

EXERCISE 13—4

Verify the following: