The Calculus Primer (2011)
Part XIII. Special Methods of Integration
Chapter 50. TABLES OF INTEGRALS
13—7. Use of Integral Tables. The reader will find a list of integrals given on pages 371–378. Such a collection of formulas should not be regarded as a substitute for a good working knowledge of methods of integration. It is far more important for the reader to cultivate facility in recognizing forms, and to become proficient in transforming a given expression to a standard form, than it is to rely upon a table of integrals. No such table, however elaborate, is ever complete. The chief value of a table is that its use saves time.
When using a table of integrals, we note that it is arranged systematically, according to the form of the integrand. It must not be supposed that any given integrand will always be found in the table. If, upon searching the table until we find an integrand which is exactly of the form given, the integral can be written at once by substituting in the formula taken from the table. On the other hand, it may be necessary to transform a given integrand algebraically or trigonometrically in order that it will assume the exact form of some integrand given in the table before the formula in the table can be applied. The following examples will show how this is done.
EXAMPLE 1. Find ![]()
Solution. From the table, page 374, formula [39] gives
![]()
which is exactly in the form of the given integrand. Here, then, a = 5 and b = 3; hence
![]()
EXAMPLE 2. Find ![]()
Solution. From the table, page 373, formula [36] gives
![]()
where x has been replaced by v. The given integrand, however, must first be rewritten; let a = ![]() and v2 = 7x2, or v =
and v2 = 7x2, or v = ![]() x, and dv = d (
x, and dv = d (![]() x). Substituting in the formula, we obtain:
x). Substituting in the formula, we obtain:
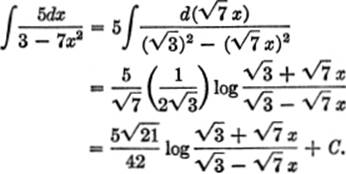
EXAMPLE 3. Find ![]()
Solution. Completing the square in the denominator:
![]()
Using formula [18], page 372, we have:
v = (3x − 2), a = ![]() , dv = 3dx.
, dv = 3dx.
Hence
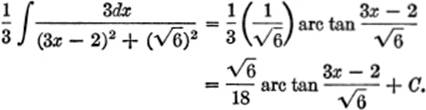
EXERCISE 13—5
Integrate the following, using the tables at the back of the book, pages 371–378; for practice, verify your result by differentiation:
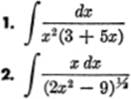
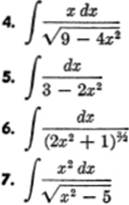
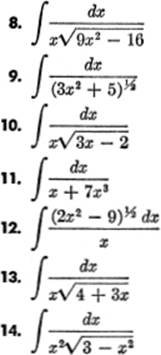
15. ![]() sin 6x cos 3x dx
sin 6x cos 3x dx