The Calculus Primer (2011)

Part XV. Integration as a Process of Summation

Chapter 58. LENGTH OF A CURVE

15—8. Differential Length of Arc. It will be recalled that in §14—6 we derived a formula for the differential length of arc, namely,

We shall now use the Fundamental Theorem to derive a formula for the length of an arc of a curve. By definition, the length of a portion of a curve means the limit of the sum of the chords as the number of points of division is increased indefinitely in such a manner that the length of each chord, at the same time, separately approaches zero as a limit.

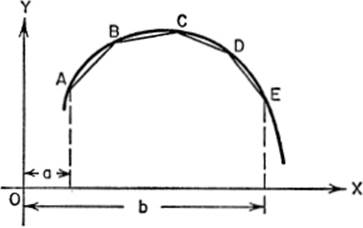
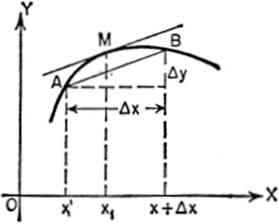
Consider the length of any one of these chords, say AB, where the coordinates of A are (x′,y′), and those of B are (x′ + Δx, y′ + Δy). It will be seen that

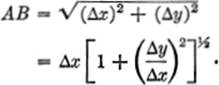
By the theorem of mean value:

where x₁ is the abscissa of point M on the curve at which the tangent is parallel to the chord.

Hence, AB = Δx[1 + f′(x₁)²]^½;

similarly,BC = Δx[1 + f′(x₂)²]^½,

CD = Δx[1 + f′(x₃)²]^½,etc.

Therefore, the length of the broken line AE is given by

Thus, by the Fundamental Theorem:

When using this formula, we must remember always to express in terms of x, as determined by the given equation.

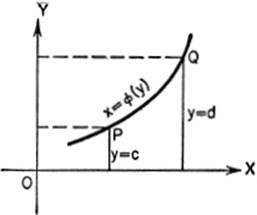
If y is used as the independent variable, the corresponding formula is:

If the equation of the curve is given in polar coordinates, the analogous formulas for the length of an arc are

When using formula [3], remember to express in terms of θ before integrating; when using [4], the quantity must be expressed in terms of ρ before integrating.

EXAMPLE 1. Find the length of the arc of the curve x² = 2py between the points where x = 0 and x = p.

Solution. x² = 2py; hence .

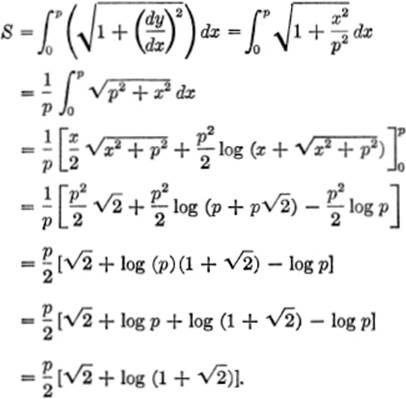
EXAMPLE 2. Find the length of the circle whose equation is x² + y² = r².

Solution. Consider the quarter-arc in the first quadrant.

From the equation, .

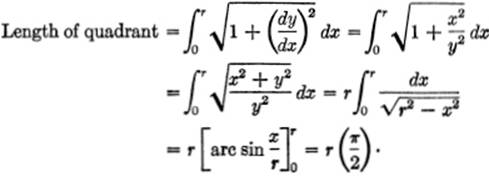
Therefore,

length of entire circle = 4 = 2πr.

EXERCISE 15—3

1. Find the length of the arc of y = x² from the origin to the point whose abscissa is 3.

2. Find the length of the arc on the logarithmic spiral ρ = e^θ from the point where θ = 0 to the point where θ = 1.

3. Find the length of the arc of y² = 4ax between the points whose abscissas are x = 0 and x = 2a.

4. Find the length of the arc of y = log cos x between the points whose abscissas are x = 0 and x = π/6.

5. Find the length of the circle whose equation is ρ = 2a cos θ.

6. Find the length of the circle whose equation is y² + (x − a)² = a². Compare your result with that for Problem 5; explain.

7. Find the length of the arc on the spiral of Archimedes, ρ = aθ, when the radius vector has made one revolution, i.e., from θ = 0 to θ = 2π.

8. Find the total length of the curve whose equation is ρ = a sec θ.

9. Find the length of the arc of e^v = 1 − x² between the points whose abscissas are x = 0 and x = .

10. Find the entire length of the curve ρ = a sin³ .