The Calculus Primer (2011)

Part XV. Integration as a Process of Summation

Chapter 59. SOLIDS OF REVOLUTION

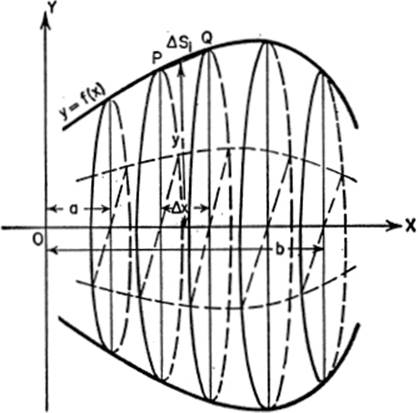
15—9. Volumes of Solids of Revolution. Consider the arc PQ of the curve y = f(x) from x = a to x = b (Fig. I). If we suppose the arc to be revolved about OX as an axis, the solid of revolution obtained (Fig. II) may be regarded as composed of a series of right circular cylinders, formed by the revolving rectangles. As Δx → 0, that is, as the number of rectangles, and therefore the number of cylinders, increases indefinitely, the sum of the volumes of the cylinders approximates more and more closely to the volume of the solid of revolution. The volume of any one of these cylinders, say the ith cylinder, is the area of its base, πy_i², multiplied by its altitude, Δx_i; in other words,

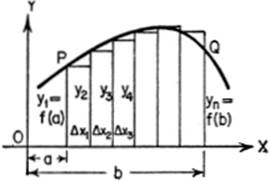
Figure I

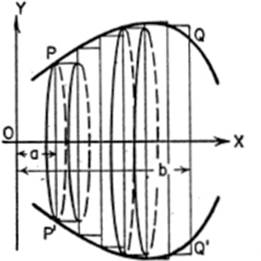
Figure II

Applying the Fundamental Theorem:

where V_x denotes the volume of the solid of revolution formed by rotating y = f(x) about the X-axis.

If the curve y = f(x) is rotated about the Y-axis, then

where the value of x in terms of y, as found from the given equation y = f(x), must be substituted before integrating, and where c and d are the limits of integration in terms of ordinates.

EXAMPLE 1. Find the volume of the sphere generated by revolving the circle x² + y² = r² about the X-axis.

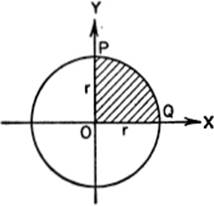
Solution. Consider the volume formed by revolving arc PQ about the X-axis, which is half the volume required. From equation [1]

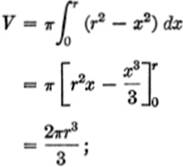
hence, volume of entire sphere =

EXAMPLE 2. Find the volume generated by the arc of the parabola x² = 4y between the points where y = 0 and y = a when revolved about the Y-axis.

Solution. Here we use formula [2]:

15—10. Area of a Surface of Revolution. If the arc of a curve y = f(x) between the abscissa x = a and x = b is revolved about the X-axis, the surface S so generated is given by the formula

The corresponding formula for the surface S_y obtained by revolving the arc from y = c to y = d about the Y-axis, is given by

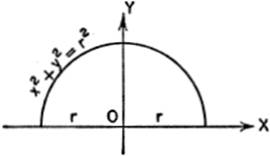
EXAMPLE 1. Find the surface of a sphere generated by revolving a semicircle of radius r about the X-axis, as shown.

Solution.

x² + y² = r²;

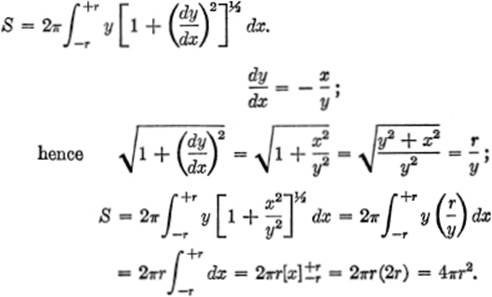
EXAMPLE 2. Find the area generated by the arc of the parabola y² = 2ax between the points where x = 0 and x = 2a when revolved about the X-axis.

Solution.

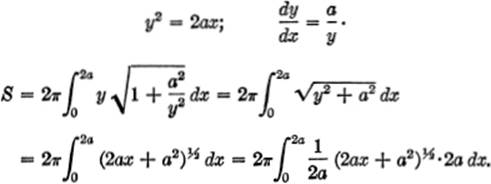
(Integrating by the substitution: u = 2ax + a², therefore du = 2a dx)

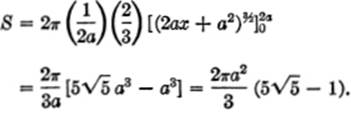
EXERCISE 15—4

1. Find the volume generated by revolving the ellipse b²x² + a²y² = a²b² about the X-axis.

2. Find the volume generated when the same ellipse (Problem 1) is revolved about the Y-axis. Prove that each result is correct by taking the special case where a = b.

3. Find the volume of the cone generated by revolving about the X-axis the segment of the line y = 3 − x cut off by the axes.

4. Find the volume of the solid generated by an arch of the sine curve, y = sin x, from x = 0 to x = π, when revolved about the X-axis.

5. Find the volume of the solid generated by revolving the arc of the parabola y² = 4px between the origin and the point for which x = 2p when revolved about the X-axis.

6. Find the volume of the doughnut-like ring, called the torus, generated by revolving the circle x² + (y − k)² = r² about the X-axis.

7. The line y = 2x is revolved about the X-axis. Find the area of the cone generated by the segment from x = 0 to x = 4.

8. A right circular cone has an altitude h = 8 and a base of radius r = 4. Find the lateral surface by-integration; check by elementary geometry.

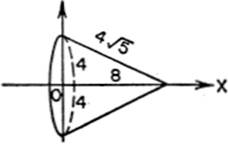
9. Find the total surface generated by revolving the parabola y² = 4x about the X-axis from the origin to the point where x = 8.

10. The arc of the parabola y² = 4px lying between the points where x = 0 and x = 2p is revolved about the X-axis; find the surface generated.

11. The segment of the line y = x + 2 from x = 0 to x = 3 is revolved about the X-axis. Find the lateral surface of the frustum of the cone generated, and check your result by elementary geometry.

12. Prove, by integration, that the lateral surface of a right circular cylinder of radius r and altitude h equals 2πrh.