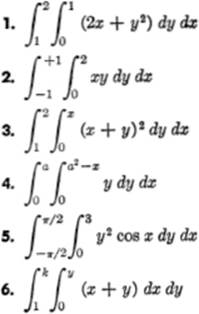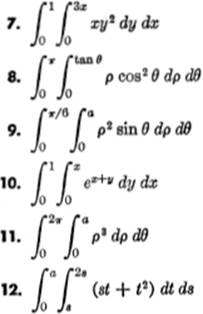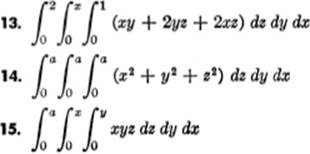The Calculus Primer (2011)

Part XVI. Successive and Partial Integration; Approximate Integration

Chapter 60. MULTIPLE INTEGRALS

16—1. Successive Integration. This is the inverse of the process of successive differentiation. Suppose it is given that

and we wish to find y. We may then write:

integrating:

Again:

integrating once more:

Finally:

and integrating,

The above analysis can also be written as follows:

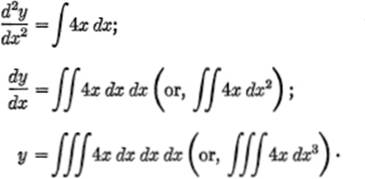
These last two are called a double integral and a triple integral, respectively. It will be seen that there is nothing new about successive integration, except that more than one constant of integration is involved. In general, a multipleintegral requires two or more successive integrations. The process is also known as repeated integration, or iterated integration.

EXAMPLE. Find y, if y = 3x² dx dx dx.

Solution.

y = 3x² dx dx dx

= (x³ + C₁) dx dx

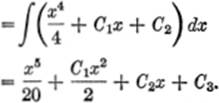
16—2. Multiple Integrals with Limits of Integration. If successive integrations are performed between limits, the constants of integration disappear.

EXAMPLE. Evaluate 3x dx dx dx.

Solution. Beginning by integrating the “inside” integral first:

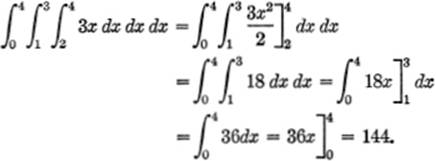
EXERCISE 16—1

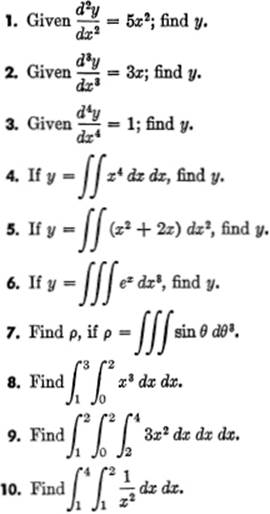
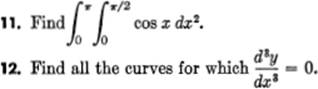
16—3. Successive Partial Integration. Just as we can find partial derivatives of a function of two or more variables, so we can also integrate the function f(x,y) in an analogous inverse process of partial differentiation. In the function f(x,y), where x and y are both independent variables, let us for a moment consider x as a constant, and let y vary; then f(x,y) becomes a function of y only. Now, under these conditions, suppose we integrate between the limits y = c and y = d; we then have:

Now the value of this integral will depend not only upon the value of y, but also upon the value of x; hence the entire expression in (1) may be regarded as a function of x. Under this condition, let us now integrate with respect to xbetween the limits x = a and x = b: the result becomes

which is generally written without the bracket as

The expression (3) is read: “the double integral of f(x,y) from y = c to y = d and from x = a to x = b.”

EXAMPLE 1. Find the value of the double integral

Solution. We perform the “y-integration” first, remembering to “hold” x constant:

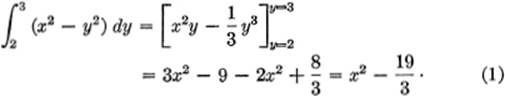
Now we perform the second integration, or the “x-integration,” upon the expression in (1), this time “holding” y constant, and integrating with respect to x:

The limits of integration need not necessarily all be constants; very often the limits of y in the first integration are themselves functions of the variable x, as shown in the next two examples.

EXAMPLE 2. Find the value of

Solution. Integrating first with respect to y, we get:

Now, integrating with respect to x:

EXAMPLE 3. Find

Solution.

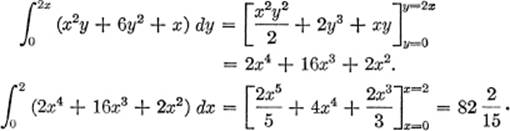
The same ideas may be extended to triple integrals.

EXAMPLE 4. Find the value of

Solution. Consider x and y both constant, and integrate with respect to the variable z:

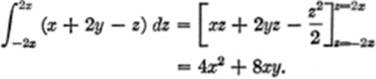
Then perform the y-integration, remembering that x is a constant:

Finally, perform the x-integration:

EXERCISE 16—2

Find the value of each of the following multiple integrals: