The Calculus Primer (2011)
Part XVI. Successive and Partial Integration; Approximate Integration
Chapter 61. AREAS AND VOLUMES
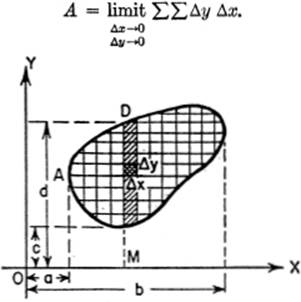
16—4. Plane Areas by Double Integration: Rectangular Coordinates. It can be shown that the area enclosed by a curve (or several curves) over a given region is given by the expression
This area can be calculated by evaluating the corresponding integral, or
Interpreting this double integral from the figure, we see that when we keep x(=OM) constant and integrate with respect to y, we are summing up all the elements in the shaded vertical strip, from y = c to y = d; then, by integrating the result of this summation with respect to x, we are finding the sum of all such vertical strips between the limits x = a and x = b, which clearly gives the total area desired. Of course, the order of integration could be reversed, in which case we should be summing up a series of horizontal strips, and the limits of both integrations would have to be changed accordingly.
In general, then, a plane area in rectangular coordinates may be found from the double integrals
where the limits of integration have been properly selected. Some areas can be found either by single integration, as we have already seen, or by double integration; in other cases, the use of double integration affords the only method of finding the area.
EXAMPLE. Find by double integration the area enclosed by the circle x2 + y2 = k2.
Solution. The area required is given by finding the area in the first quadrant by a double summation, and then multiplying by 4; hence
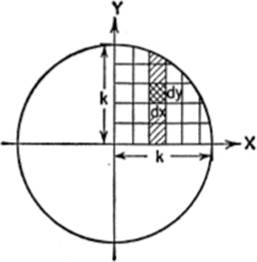
But, from the given equation, y = 
; hence
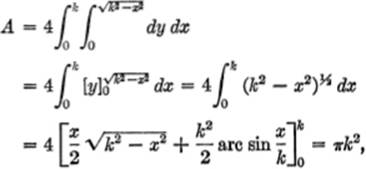
by formula [68], page 376.
16—5. Plane Areas by Double Integration: Polar Coordinates. For curves expressed in polar coordinates, the analogous formulas for finding the area by double integration are given without proof; their reasonableness may be seen intuitively from the diagram:
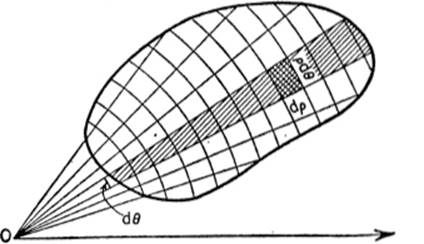
where the limits of integration are properly chosen. Similarly, the area between two curves ρ = f(θ) and ρ = ϕ(θ) is given by the formula
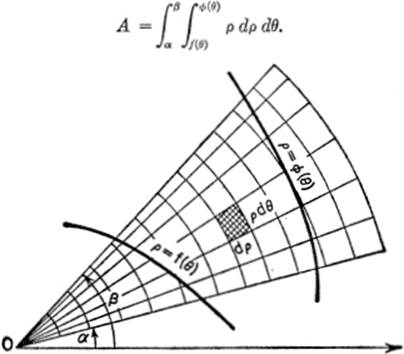
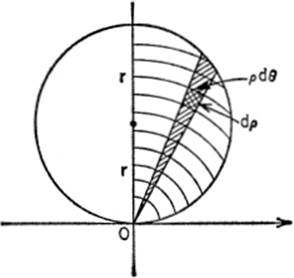
EXAMPLE. Find by double integration the area of the circle ρ = 2r sin θ.
Solution. The area of the semicircle from θ = 0 to θ = π/2 is given by
Integrating first with respect to ρ:
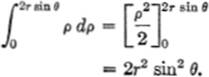
Hence:
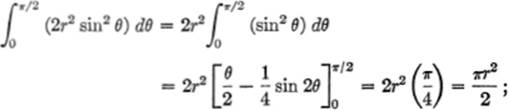
therefore the entire circle 
16—6. Area between Two Curves. The method of summation is conveniently employed for finding the area included between two plane curves.
EXAMPLE 1. Find the area included between the lines 2y = 3x, 3y = 2x, and x = 6.
Solution. The area in question is given by
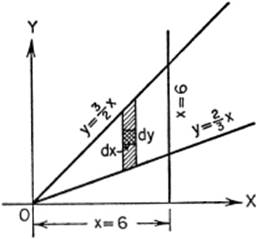
since, in summing up a vertical strip like the one shown, y ranges in value from 
to 
, and in summing up all such vertical strips, x ranges from x = 0 to x = 6.
Therefore:
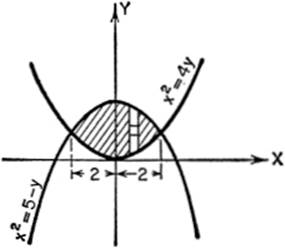
EXAMPLE 2. Find by double integration the area included between x2 = 4y and x2 = 5 − y.
Solution. The desired area is given by summing up vertical strips such as shown in the figure. To express the area of one such strip, we integrate between the limits given by the equations when solved for y, that is, y = 
and y = 5 − x2. To sum up all the vertical strips, we use the limits x = −2 to x = +2, the abscissas of the points of intersection of the curves.
Hence:
16—7. Volumes by Triple Integration. The ideas developed in the preceding sections can be extended to the problem of finding volumes by triple integration. The general formula for the volume of a solid is given by
where the limits of integration are found from the equations of the bounding surfaces. We shall illustrate by the following example.
EXAMPLE. Find the volume of the ellipsoid whose equation is
Solution. Consider, for purposes of summation, the portion of the solid lying in the first octant, which is one-eighth of the total volume. To sum up the differential rectangular parallelopipeds with their edges parallel to the respective axes, we take as the limits for z the values z = 0 and z = 
; for the limits of y, we take y = 0 for the lower limit, and 
for the upper limit; for the limits of x, we take x = 0 and x = a. The volume of the entire ellipsoid thus equals
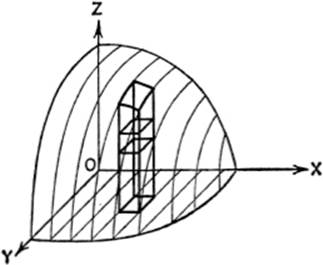
Now to integrate 
, we note that formula [68], page 376, can be applied, where the 
corresponds to the constant “a2” of formula [68], and the 
corresponds to the “x2” of formula [68]. Applying the formula, and substituting the limits, we obtain, finally, the volume V = 
πabc. The details are left as an exercise for the reader. It will be noted that in the special case where a = b = c = r, the ellipsoid becomes a sphere, and the volume becomes πr3.
EXERCISE 16—3
1. Find, by double integration, the area under the parabola x2 = 4y, from x = 0 to x = 4; verify your result by using single integration.
2. Find, by double integration, the area enclosed by the curve y2 = 4 + x and the line x = 4.
3. Find, by double integration, the area bounded by the curves y = sin x, y = cos x, and the Y-axis.
4. Find the area, by double integration, under the curve y = ex, between the lines x = 0 and x = 2.
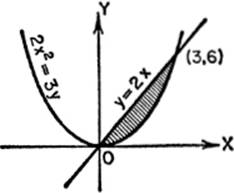
5. Find, by double integration, the area included by the parabola 2x2 = 3y and the line y = 2x.
6. Find, by double integration, the area between the curve 8y2 = x3 and the line x = y.
7. Find by double integration the area included between the parabolas y2 = 4 + x and y2 = 4 − 2x.
8. Find by double integration the area of the circle ρ = 10 cos θ.
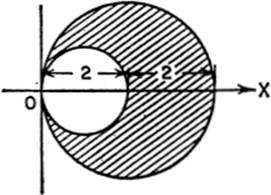
9. Find the area of the upper half of the cardioid
ρ = a(l − cos θ).
10. Find by double integration the area between the circles
ρ = 2 cos θ and ρ = 4 cos θ.
Hint: Here θ ranges from
−π/2 to π/2.