The Calculus Primer (2011)

Part II. The Derivative of a Function

Chapter 7. DIFFERENTIATION: FINDING THE DERIVATIVE

2—7. The Process of Differentiation. The operation of finding the derivative of a function is called differentiation. The derivative, as we have already seen, is written . This symbol is read: “the derivative of y with respect to x,” or, sometimes, the “x-derivative of y” It may be written in a variety of ways, but they all denote the same thing: thus

orf(x) = f′(x).

We shall now illustrate the operation of differentiation, and then formulate a General Rule of procedure.

EXAMPLE 1.Differentiate: y = 3x − 2.

Solution.

y = 3x − 2.(1)

Let x take on an increment Δx, and let the corresponding increment in y be Δy.

Theny + Δy = 3(x + Δx) − 2,

ory + Δy = 3x + 3Δx − 2.(2)

Subtract equation (1) from equation (2):

y + Δy = 3x + 3Δx − 2

y= 3x − 2

Δy = 3Δx(3)

Now divide equation (3) by Δx:

Finally, let Δx → 0:

= 3,

or = 3.

EXAMPLE 2.Differentiate: y = x² + 5.

Solution.

y = x² + 5.(1)

y + Δy = (x + Δx)² + 5,

ory + Δy = x² + 2x·Δx+ (Δx)² + 5.(2)

Subtracting (1) from (2):

y + Δy = x² + 2x·Δx + (Δx)² + 5

y= x²+ 5

Δy = 2x·Δx + (Δx)²(3)

Dividing (3) by Δx:

= 2x + Δx.

Let Δx → 0:

= 2x,

or = 2x.

EXAMPLE 3.Differentiate: y = x² + 3x + 8.

Solution.

y + Δy = (x + Δx)² + 3(x + Δx) + 8

y + Δy = x² + 2x·Δx + (Δx)² + 3x + 3Δx + 8

y= x²+ 3x+ 8

Δy = 2x·Δx + (Δx)² + 3Δx

Dividing through by Δx:

= 2x + Δx + 3.

Let Δx → 0:

= 2x + 3.

or = 2x + 3.

EXAMPLE 4.Differentiate: y = x³.

Solution.y + Δy = (x + Δx)³.

y + Δy = x³ + 3x²·Δx + 3x·(Δx)² + (Δx)³.

Subtracting:Δy = 3x²·Δx + 3x (Δx)² + (Δx)³.

Dividing: = 3x² + 3x(Δx) + (Δx)².

Passing to the limit:

= 3x²,

for, as Δx → 0, the terms 3x(Δx) and (Δx)² vanish.

EXAMPLE 5.Differentiate: y = .

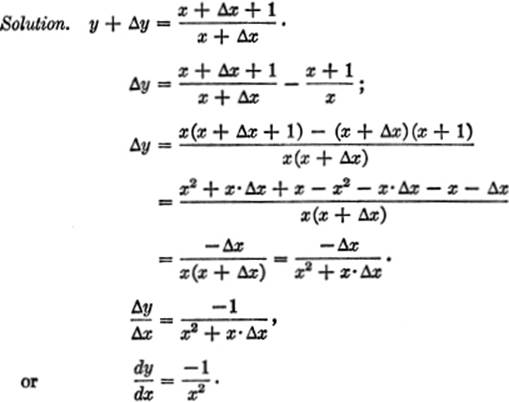
2—8. The General Rule for Differentiation. We may now formulate the “four-step” rule for differentiating a function, as follows:

Step 1. Substitute (x + Δx) for x in the given equation, thus giving y a new corresponding value, (y + Δy).

Step 2. Subtract the given equation from the equation obtained in Step 1, thus obtaining an expression for Δy.

Step 3. Divide the equation obtained in Step 2 by Δx, thus obtaining a value for .

Step 4. Find the limit of as Δx approaches zero as a limit. This limit is the required derivative.

EXERCISE 2—1

Differentiate each of the following functions by the General Rule:

1. y = 2x − 3

2. y = 4 − x²

3. y = 2x² + 3x

4. y = 10x²

5. y = x² − x + 6

6. y = 3x² − 2x + 1

7. y = 2x³ + 3

8. y = x³ − 2x

9. y = (x + 1)(x − 2)

10. y = (2x − l)(3x + 2)

11.y =

12.y =

13.y =

14.y =

15.y =

16.y =

2—9. Finding the Tangent to a Curve. In the light of the discussion in §2—6, we are now able to find the slope of the tangent to a given curve at a given point, or the slope of a curve at any desired point, provided, of course, that the equation of the curve is given.

EXAMPLE 1.Find the slope of the curve y = x² + 6 at the point where x = 5.

Solution.y = x² + 6.

By the General Rule,

= 2x + Δx,

and = 2x.

Hence, when x = 5, = 2(5) = 10. The slope of the tangent to y = x² + 6 at the point where x = 5 is 10, as is the slope of the curve at that point. The inclination of the tangent is ϕ = arc tan 10, or approximately 84°17′.

EXAMPLE 2.Find the slope of the curve y = 3x² − 4x + 8 at the point where x = 3.

Solution.By the General Rule,

= 6x − 4 + 3(Δx),

and = 6x − 4.

Hence, when x = 3, = 6(3) − 4 = 14, the required slope.

EXERCISE 2—2

By differentiating by the General Rule, find the slope of the tangent to each of the following curves at the point indicated:

1. y = x² − 5, where x = 6.

2. y = 4x² + 3, where x = 1.

3. y = x² − 3x + 6, where x = 4.

4. y = 3x² + 4x, where x = − 2.

5. y = (x + 3)², where x = 0.

6. y = x³ − x², where x = −3.

7. y = x³ + 8, where x = −2.

8. y = x⁴ − 1, where x = .