Easy Mathematics Step-by-Step (2012)
Chapter 9. Ratios and Proportions
In this chapter, you learn about ratios and proportions.
Ratio Concepts
A ratio is a comparison by division of two quantities having the same units. Suppose the lengths of the radii of two circles are in the ratio of 3 to 5. If the radius of the first circle is 3 in, then the radius of the second circle is 5 in. That is, the radius of the first circle is ![]() as long as the radius of the second circle. Ratios can be expressed in several different forms: 3 to 5, 3:5,
as long as the radius of the second circle. Ratios can be expressed in several different forms: 3 to 5, 3:5, ![]() ,
, ![]() , 0.6, or 60%. The context of the discussion at the time usually dictates the form preferred. A ratio is a pure number—it has no units. The units “cancel” out as in
, 0.6, or 60%. The context of the discussion at the time usually dictates the form preferred. A ratio is a pure number—it has no units. The units “cancel” out as in ![]() . Fractions, percents, and decimals are ratios. If the items compared have units that cannot be “canceled” such as
. Fractions, percents, and decimals are ratios. If the items compared have units that cannot be “canceled” such as ![]() , then the comparison is called a rate or a scale.
, then the comparison is called a rate or a scale.
Be careful when writing ratios. For instance, the comparison of 3 in to 5 ft is not a ratio because both are not expressed in the same units.
Proportion Concepts
The mathematical statement that two ratios (or rates or scales) are equal is a proportion. The statement ![]() is a proportion and is commonly read as “2 is to 3 as 4 is to 6.” This can also be written as
is a proportion and is commonly read as “2 is to 3 as 4 is to 6.” This can also be written as ![]() , although for computations the fractional form is necessary. The fundamental property of proportions is that
, although for computations the fractional form is necessary. The fundamental property of proportions is that ![]() if and only if
if and only if ![]() The products ad and bc are the cross products.
The products ad and bc are the cross products.
![]()
In a proportion, the cross products are equal to each other.
Proportions and proportional thinking pervade such diverse topics as medicine dosage, application of fertilizer to a lawn, and oil additives in gasoline for outboard motors. Consequently, you should master the basics presented here to prepare for any real-world applications you might encounter.
Solving Proportions
If the values of three of the four terms of a proportion are known, then the value of the fourth term can be determined by using the fundamental property of proportions.
Problem Set up a proportion and solve for the unknown term.
a. A number n compared to 45 is the same as 7 compared to 15. Find n.
b. 38 is to 640 as 152 is to the number n. Find n.
Solution
a. A number n compared to 45 is the same as 7 compared to 15. Find n.
![]() Step 1. Write a proportion.
Step 1. Write a proportion.
![]()
Step 2. Solve the proportion.
Find a cross product you can calculate.
![]()
Divide by the numerical term you didn’t use.
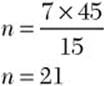
Step 3. Check.
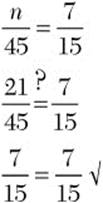
b. 38 is to 640 as 152 is to the number n. Find n.
![]() Step 1. Write a proportion.
Step 1. Write a proportion.
![]()
Step 2. Solve the proportion.
Find a cross product you can calculate.
![]()
Divide by the numerical term you didn’t use.
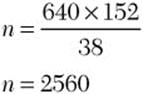
Step 3. Check.
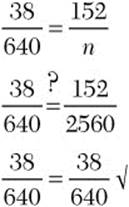
Note: The fraction on the left initially could have been reduced.
It often simplifies the arithmetic in a problem to reduce as much as possible initially.
Solving Application Problems Involving Proportions
When you have an application problem involving proportions, look for a sentence or phrase in the problem that provides the information you need for the left portion of the proportion, and then look for another sentence or phrase that gives you the information you need for the right portion of the proportion.
Problem On a map, the distance between two cities is 13.5 in. On the map scale 0.5 in represents 20 mi. How far is it, in miles, between the two cities?
Solution This problem is a proportion problem involving a map scale. Information for the left portion of the proportion is in the first sentence of the problem, and information for the right portion of the proportion is in the second sentence.
![]() Step 1. Use the first sentence to write the left portion of the proportion.
Step 1. Use the first sentence to write the left portion of the proportion.
Let d be the unknown distance. Then d corresponds to 13.5 in:
![]()
Step 2. Use the second sentence to write the right portion of the proportion.
![]()
Step 3. Write the proportion by setting the left portion equal to the right portion.
![]()
Notice that the units in the left portion match up with the units in the right portion.
Always check whether your units match up when you write a proportion. If you have miles in the numerator and inches in the denominator on the left, then you should have miles in the numerator and inches in the denominator on the right. If the units in the left and right portions don’t match up, then your proportion is incorrect.
Step 4. Solve the proportion.
Find a cross product you can calculate.
![]()
Divide by the numerical term you didn’t use.
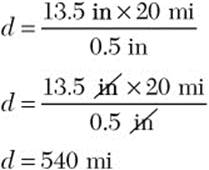
Notice that the units work out to be miles, which is what you should expect because d is a distance.
In application problems, always check whether the units work out to be appropriate units for the unknown quantity.
Step 5. Check.
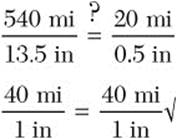
You should always mentally check whether the answer makes sense. For instance, if 0.5 in represents 20 mi, then 1 in represents 40 mi, so 10 in should be 400 mi. Thus, an answer of 540 mi for 13.5 in does make sense.
Problem If 25 ft of wire weighs 3 lb, what is the weight of 8 ft of this wire?
Solution This problem is a proportion problem involving lengths and weights. Information for the left portion of the proportion is in the first part of the problem question, and information for the right portion of the proportion is in the second part of the problem question.
![]() Step 1. Use the first part of the problem question to write the left portion of the proportion.
Step 1. Use the first part of the problem question to write the left portion of the proportion.
![]()
Step 2. Use the second part of the problem question to write the right portion of the proportion.
![]()
Step 3. Write the proportion by setting the left portion equal to the right portion.
![]()
Notice that the units in the left portion match up with the units in the right portion.
Step 4. Solve the proportion.
Find a cross product you can calculate.
(3 lb)(8 ft)
Divide by the numerical term you didn’t use.
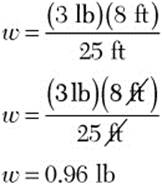
Notice that the units work out to be pounds, which is what you should expect because w is a weight.
Step 5. Check.
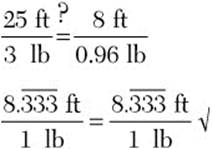
Problem The ratio of a propeller rate to that of the engine is 2:3. If the engine is turning at a rate of 4800 revolutions per minute (rpm), what is the propeller rate?
Solution This is a proportion problem involving two ratios. The first ratio is in the first sentence, and the second ratio is in the question. Let R be the unknown propeller rate and compare the ratios.
![]() Step 1. Write a proportion.
Step 1. Write a proportion.
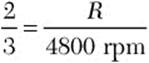
Step 2. Solve the proportion
Find a cross product you can calculate.
![]()
Divide by the numerical term you didn’t use.

Step 3. Check.
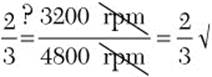
Using Proportions to Solve Percent Problems
Percent problems can be solved using a “percent proportion,” which has the following form:
![]()
where
n = the number in front of the % sign
part = the quantity that is near the word is (when the word is occurs in the problem)
whole = the quantity that immediately follows the word of
The relationship among the three elements n, part, and whole can be explained in a percent statement like this:
The part is n% of the whole.
The secret to solving percent problems is being able to identify the three elements correctly. Start with n and the whole because they are usually easier to find. The part will be the other amount in the problem. The value of two of the elements will be given in the problem, and you will be solving for the third element. After you identify the three elements, substitute the two you know into the percent proportion and solve for the one that you don’t know.
Problem Use a percent proportion to solve the given percent problem.
a. You inherited 15% of $9000. How much money did you inherit?
b. A student scored 60 out of 80 questions. What is the student’s percent grade?
c. A toy is on sale for $13. This sale price is 80% of the regular price of the toy. What is the regular price?
d. What is 30% of 140?
e. Twenty-five is 40% of what number?
f. Twenty-seven out of 40 is what percent?
Solution
a. You inherited 15% of $9000. How much money did you inherit?
![]() Step 1. Write the percent proportion.
Step 1. Write the percent proportion.
![]()
Step 2. Set up the percent proportion using $9000 as the whole and 15 as n. Let p be the part inherited.
![]()
Step 3. Solve the proportion.
![]()
Step 4. Check.
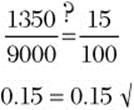
Step 5. Answer the question.
$1350 is the amount inherited.
b. A student scored 60 out of 80 questions. What is the student’s percent grade?
![]() Step 1. Write the percent proportion.
Step 1. Write the percent proportion.
![]()
Step 2. Set up the percent proportion using 80 as the whole and 60 as the part. Let n be the percent number.
![]()
Step 3. Solve the proportion.
![]()
Step 4. Check.
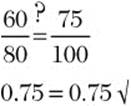
Step 5. Answer the question.
The percent score is 75%.
c. A toy is on sale for $13. This sale price is 80% of the regular price of the toy. What is the regular price?
![]() Step 1. Write the percent proportion.
Step 1. Write the percent proportion.
![]()
Step 2. Set up the percent proportion using the regular price as the whole and $13 as the part. Let w be the regular price.
![]()
Step 3. Solve the proportion.
![]()
Step 4. Check.
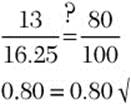
Step 5. Answer the question.
The regular price is $16.25.
d. What is 30% of 140?
![]() Step 1. Write the percent proportion.
Step 1. Write the percent proportion.
![]()
Step 2. Set up the percent proportion using 140 as the whole and ![]() as 30%. Let p be the part.
as 30%. Let p be the part.
![]()
Step 3. Solve the proportion.
![]()
Step 4. Check.
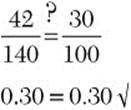
Step 5. Answer the question.
30% of 140 is 42.
e. Twenty-five is 40% of what number?
![]() Step 1. Write the percent proportion.
Step 1. Write the percent proportion.
![]()
Step 2. Set up the percent proportion using w as the whole, ![]() as 40%, and 25 as the part.
as 40%, and 25 as the part.
![]()
Step 3. Solve the proportion.
![]()
Step 4. Check.
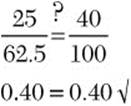
Step 5. Answer the question.
25 is 40% of 62.5.
f. Twenty-seven out of 40 is what percent?
![]() Step 1. Write the percent proportion.
Step 1. Write the percent proportion.
![]()
Step 2. Set up the percent proportion using 40 as the whole and 27 as the part. Let n be the percent number.
![]()
Step 3. Solve the proportion.
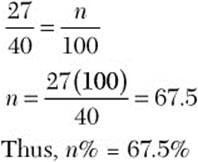
Step 4. Check.
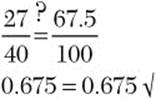
Step 5. Answer the question.
27 out of 40 is 67.5%.
 Exercise 9
Exercise 9
1. If 14 oz of salt is mixed with 5 oz of pepper, what is the ratio of salt to pepper?
2. Solve the proportion ![]() for n.
for n.
3. In a paint mixture that uses 2 parts of white paint to 5 parts of blue paint, how many quarts of white paint are needed to mix with 20 quarts of blue paint?
4. A stake 10 ft high casts a shadow 8 ft long at the same time that a tree casts a shadow 60 ft long. What is the height of the tree?
5. If 7 g of iron combines with 4 g of sulfur to form iron sulfide, how much sulfur will combine with 56 g of iron?
6. The tax on a property valued at $12,000 is $800. Assuming the tax rate is the same, what is the value of a property taxed at $1100?
7. Ninety-two is 80% of what number?
8. What is 35% of 80?
9. You buy a $5000 savings certificate that pays 4% simple annual interest. How much interest will you earn in 6 months?
10. Forty-five out of 120 is what percent?
11. If a jet plane can travel 4500 km in 5 hr, how many kilometers can it travel in 25 min?
12. A map has a scale of 1 in = 15 mi. How much distance is represented by 18 in?
13. What percent of 7580 is 454.8?
14. Calcium and chlorine combine in the weight ratio of 36:64. How much chlorine will combine with 5 g of calcium?