Easy Mathematics Step-by-Step (2012)
Chapter 10. Roots and Radicals
In this chapter, you learn about roots and radicals.
Square Roots
You square a number by multiplying the number by itself. For instance, the square of 4 is ![]() . Also, the square of –4 is
. Also, the square of –4 is ![]() . Thus, 16 is the result of squaring 4 or –4. The reverse of squaring is finding the square root. The two square roots of 16 are 4 and –4. Every positive number has two square roots that are equal in absolute value, but opposite in sign. The number 0 has only one square root, namely, 0.
. Thus, 16 is the result of squaring 4 or –4. The reverse of squaring is finding the square root. The two square roots of 16 are 4 and –4. Every positive number has two square roots that are equal in absolute value, but opposite in sign. The number 0 has only one square root, namely, 0.
The product of two negative numbers is positive.
When you are working with real numbers (which are the numbers you work with in this book), don’t try to find square roots of negative numbers because not one real number will multiply by itself to give a negative number.
Problem Find the two square roots of the given number.
a. 25
b. 100
c. ![]()
d. 0.49
Solution
![]()
![]() Step 1. Find a positive number whose square is 25.
Step 1. Find a positive number whose square is 25.
![]() , so 5 is the positive square root of 25.
, so 5 is the positive square root of 25.
Step 2. Find a negative number whose square is 25.
![]() , so –5 is the negative square root of 25.
, so –5 is the negative square root of 25.
Step 3. Write the two square roots of 25.
5 and –5 are the two square roots of 25.
b. 100
![]() Step 1. Find a positive number whose square is 100.
Step 1. Find a positive number whose square is 100.
![]() , so 10 is the positive square root of 100.
, so 10 is the positive square root of 100.
Step 2. Find a negative number whose square is 100.
![]() , so –10 is the negative square root of 100.
, so –10 is the negative square root of 100.
Step 3. Write the two square roots of 100.
10 and –10 are the two square roots of 100.
![]()
![]() Step 1. Find a positive number whose square is
Step 1. Find a positive number whose square is ![]() .
.
![]() , so
, so ![]() is the positive square root of
is the positive square root of ![]() .
.
Step 2. Find a negative number whose square is ![]() .
.
![]() , so,
, so, ![]() is the negative square root of
is the negative square root of ![]() .
.
Step 3. Write the two square roots of ![]() .
.
![]() and
and ![]() are the two square roots of
are the two square roots of ![]() .
.
d. 0.49
![]() Step 1. Find a positive number whose square is 0.49.
Step 1. Find a positive number whose square is 0.49.
(0.7)(0.7) = 0.49, so 0.7 is the positive square root of 0.49.
Step 2. Find a negative number whose square is 0.49.
(–0.7)(–0.7) = 0.49, so –0.7 is the negative square root of 0.49.
Step 3. Write the two square roots of 0.49.
0.7 and –0.7 are the two square roots of 0.49.
Principal Square Roots and Radicals
You use the symbolism ![]() , read as “the square root of 16,” to represent the positive square root of 16. Thus,
, read as “the square root of 16,” to represent the positive square root of 16. Thus, ![]() . This number is the principal square root of 16. Thus, the principal square root of 16 is 4. The symbol
. This number is the principal square root of 16. Thus, the principal square root of 16 is 4. The symbol ![]() is the square root symbol. Using this notation, you indicate the negative square root of 16 as
is the square root symbol. Using this notation, you indicate the negative square root of 16 as ![]() . Thus,
. Thus, ![]() . The expression
. The expression ![]() is a radical. The number under the
is a radical. The number under the ![]() symbol is the radicand.
symbol is the radicand.
![]() is the square root of a negative number. No real number multiplies by itself to give –16.
is the square root of a negative number. No real number multiplies by itself to give –16.
As discussed earlier, every positive number has a positive and a negative square root. The positive square root is the principal square root of the number. The principal square root of 0 is 0. The ![]() symbol always designates the principal square root. Thus,
symbol always designates the principal square root. Thus, ![]() , not –4 or
, not –4 or ![]()
The principal square root is always one number and that number is either positive or 0.
The ![]() symbol always gives one number as the answer and that number is either positive or 0.
symbol always gives one number as the answer and that number is either positive or 0.
Problem Find the indicated root.
![]()
![]()
![]()
![]()
![]()
![]()
Solution
![]()
![]() Step 1. The principal square root of 81 is the positive square root of 81, so find the positive number whose square is 81.
Step 1. The principal square root of 81 is the positive square root of 81, so find the positive number whose square is 81.
9 × 9 = 81, so 9 is the positive square root of 81.
Step 2. State the principal square root of 81.
![]()
![]() . The square root symbol always gives just one number as the answer and that number is either positive or 0! If you want
. The square root symbol always gives just one number as the answer and that number is either positive or 0! If you want ![]() , then do this:
, then do this: ![]()
![]()
![]() Step 1. The principal square root of 100 is the positive square root of 100, so find the positive number whose square is 100.
Step 1. The principal square root of 100 is the positive square root of 100, so find the positive number whose square is 100.
![]() , so 10 is the positive square root of 10.
, so 10 is the positive square root of 10.
Step 2. State the principal square root of 100.
![]() , so 10 is the positive square root of 10.
, so 10 is the positive square root of 10.
![]() . You do not divide by 2 to get a square root.
. You do not divide by 2 to get a square root.
![]()
![]() Step 1. The principal square root of
Step 1. The principal square root of ![]() is the positive square root of
is the positive square root of ![]() , so find the positive number whose square is
, so find the positive number whose square is ![]() .
.
![]() , so
, so ![]() is the positive square root of
is the positive square root of ![]() .
.
Step 2. State the principal square root of ![]() .
.
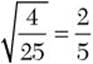
![]()
![]() Step 1. The principal square root of 0.25 is the positive square root of 0.25, so find the positive number whose square is 0.25.
Step 1. The principal square root of 0.25 is the positive square root of 0.25, so find the positive number whose square is 0.25.
0.5 × 0.5 = 0.25, so 0.5 is the positive square root of 0.25.
Step 2. State the principal square root of 0.25.
![]()
e. ![]()
![]() Step 1. State that the principal square root of 0 is 0.
Step 1. State that the principal square root of 0 is 0.
![]()
![]()
![]() Step 1. Add 9 and 16 because you want the principal square root of the quantity 9 Δ 16.
Step 1. Add 9 and 16 because you want the principal square root of the quantity 9 Δ 16.
![]()
Always treat the ![]() symbol as a grouping symbol.
symbol as a grouping symbol.
Step 2. The principal square root of 25 is the positive square root of 25, so find the positive number whose square is 25.
5 × 5 = 25, so 5 is the positive square root of 25.
Step 3. State the principal square root.
![]()
![]()
Perfect Squares
A number that is an exact square of another number is a perfect square. For instance, 4, 9, 16, and 25 are perfect squares. Here is a helpful list of principal square roots of some perfect squares.
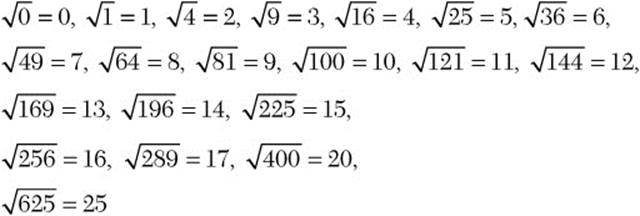
Working with square roots will be much easier for you if you memorize the list of square roots. Make flash cards to help you do this.
Also, fractions and decimals can be perfect squares. For instance, ![]() is a perfect square because
is a perfect square because ![]() equals
equals ![]() , and 0.36 is a perfect square because 0.36 equals (0.6)(0.6). If a number is not a perfect square, then you can indicate its square roots by using the square root symbol. For instance, the two square roots of 15 are
, and 0.36 is a perfect square because 0.36 equals (0.6)(0.6). If a number is not a perfect square, then you can indicate its square roots by using the square root symbol. For instance, the two square roots of 15 are ![]() and
and ![]()
Cube Roots
The product of a number used as a factor three times is the cube of that number. For instance, 64 is the cube of 4 because ![]() and, similarly, –64 is the cube of –4 because –4 · –4 · –4 = –64. The reverse of cubing is finding the cube root. Every number has one cube root, called its principal cube root. For example, because
and, similarly, –64 is the cube of –4 because –4 · –4 · –4 = –64. The reverse of cubing is finding the cube root. Every number has one cube root, called its principal cube root. For example, because ![]() , 4 is the principal cube root of 64. Likewise, because –4 · –4 · –4 = –64, –4 is the principal cube root of –64. As you can see, the principal cube root of a positive number is positive, and the principal cube root of a negative number is negative. You use the cube root symbol
, 4 is the principal cube root of 64. Likewise, because –4 · –4 · –4 = –64, –4 is the principal cube root of –64. As you can see, the principal cube root of a positive number is positive, and the principal cube root of a negative number is negative. You use the cube root symbol ![]() (read as “the cube root of”) to designate the principal cube root. The small number 3 in the symbol indicates that the cube root is desired. This number is the index of the radical. Thus,
(read as “the cube root of”) to designate the principal cube root. The small number 3 in the symbol indicates that the cube root is desired. This number is the index of the radical. Thus, ![]() and
and ![]() .
.
Notice that you can find cube roots of negative numbers; negative numbers have negative cube roots.
Here is a list of principal cube roots of some perfect cubes that are useful to know.
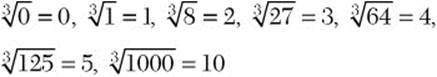
If no index is written on a radical as in ![]() , then the index is understood to be 2 and the radical indicates the principal square root.
, then the index is understood to be 2 and the radical indicates the principal square root.
You will find it worth your while to memorize the list of cube roots.
If a number is not a perfect cube, then you indicate its principal cube root by using the cube root symbol. For instance, the principal cube root of ![]() .
.
Problem Find the indicated root.
![]()
![]()
![]()
![]()
![]()
Solution
![]()
![]() Step 1. Find the positive number that you use as a factor three times to get 27.
Step 1. Find the positive number that you use as a factor three times to get 27.
![]()
Step 2. State the principal cube root of 27.
![]()
![]() You do not divide by 3 to get a cube root.
You do not divide by 3 to get a cube root.
![]()
![]() Step 1. Find the negative number that you use as a factor three times to get
Step 1. Find the negative number that you use as a factor three times to get
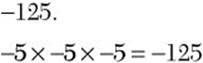
Step 2. State the principal cube root of –125.
![]()
![]()
![]() Step 1. Find the positive number that you use as a factor three times to get
Step 1. Find the positive number that you use as a factor three times to get
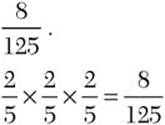
Step 2. State the principal cube root of ![]() .
.
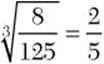
![]()
![]() Step 1. Find the positive number that you use as a factor three times to get 0.008.
Step 1. Find the positive number that you use as a factor three times to get 0.008.
(0.2)(0.2)(0.2) = 0.008
Step 2. State the principal cube root of 0.008.
![]()
![]()
![]() Step 1. Find the negative number that you use as a factor three times to get –1.
Step 1. Find the negative number that you use as a factor three times to get –1.
![]()
Step 2. State the principal cube root of –1.
![]()
 Exercise 10
Exercise 10
For 1–4, find the two square roots of the given number.
1. 144
![]()
3. 0.64
4. 400
For 5–10, find the indicated root, if possible.
![]()
![]()
![]()
![]()
![]()
![]()