Easy Mathematics Step-by-Step (2012)
Chapter 11. Algebraic Expressions
This chapter presents a discussion of algebraic expressions. It begins with the basic terminology that is critical to your understanding of the concept of an algebraic expression.
Algebraic Terminology
A variable holds a place open for a number (or numbers, in some cases) whose value may vary. You usually express a variable as an upper- or lowercase letter (e.g., x, y, z, A, B, or C); for simplicity, the letter is the “name” of the variable. In problem situations, you use variables to represent unknown quantities. Although a variable may represent any number, in many problems, the variables represent specific numbers, but the values are unknown.
You can think of variables as numbers in disguise. Not recognizing that variables represent numbers is a common mistake.
A constant is a quantity that has a fixed, definite value that does not change in a problem situation. For example, all the real numbers are constants, including numbers whose units are units of measure such as 5 feet, 60 degrees, 100 pounds, and so forth. Also, the two special irrational numbers π and e are constants.
Recall that the real numbers are the natural numbers, the whole numbers, the integers, all positive and negative fractions and decimals, and all irrational numbers.
Even though the number π is represented by a Greek letter, π is not a variable. The number π is an irrational constant whose approximate value to two decimal places is 3.14. Similarly, the number e is an irrational constant whose approximate value to two decimal places is 2.72.
Problem Name the variable(s) and constant(s) in the given expression.
![]() , where F is the number of degrees Fahrenheit
, where F is the number of degrees Fahrenheit
![]() , where d is the measure of the diameter of a circle
, where d is the measure of the diameter of a circle
Solution
![]() , where F is the number of degrees Fahrenheit
, where F is the number of degrees Fahrenheit
![]() Step 1. Recall that a letter names a variable whose value may vary.
Step 1. Recall that a letter names a variable whose value may vary.
Step 2. Name the variable(s).
The letter F stands for the number of degrees Fahrenheit and can be any number, and so it is a variable.
Step 3. Recall that a constant has a fixed, definite value.
Step 4. Name the constant(s).
The numbers ![]() and 32 have fixed, definite values that do not change, and so they are constants.
and 32 have fixed, definite values that do not change, and so they are constants.
![]() , where d is the measure of the diameter of a circle
, where d is the measure of the diameter of a circle
![]() Step 1. Recall that a letter names a variable whose value may vary.
Step 1. Recall that a letter names a variable whose value may vary.
Step 2. Name the variable(s).
The letter d stands for the measure of the diameter of a circle and can be any nonnegative number, and so it is a variable.
Step 3. Recall that a constant has a fixed, definite value.
Step 4. Name the constant(s).
The number π has a fixed, definite value that does not change, and so it is a constant.
If there is a number immediately next to a variable (normally, preceding it), that number is the numerical coefficient of the variable. If there is no number written immediately next to a variable, it is understood that the numerical coefficient is 1.
Problem State the numerical coefficient of the variable.
![]()
b. x
![]()
Solution
![]()
![]() Step 1. Identify the numerical coefficient by observing that the number –5 immediately precedes the variable x.
Step 1. Identify the numerical coefficient by observing that the number –5 immediately precedes the variable x.
–5 is the numerical coefficient of x.
b. x
![]() Step 1. Identify the numerical coefficient by observing that no number is written immediately next to the variable x, so the numerical coefficient is understood to be 1.
Step 1. Identify the numerical coefficient by observing that no number is written immediately next to the variable x, so the numerical coefficient is understood to be 1.
1 is the numerical coefficient of x.
The numerical coefficient of x is not 0. The numerical coefficient of x is understood to be 1.
![]()
![]() Step 1. Identify the numerical coefficient by observing that the number 20 immediately precedes the variable x.
Step 1. Identify the numerical coefficient by observing that the number 20 immediately precedes the variable x.
20 is the numerical coefficient of x.
Writing variables and coefficients or two or more variables (with or without constants) side by side with no multiplication symbol in between is a way to show multiplication. Thus, –5x means –5 times x, and 2xyz means 2 times x times y times z. Also, a number or variable written immediately next to a grouping symbol indicates multiplication. For instance, ![]() means 6 times the quantity
means 6 times the quantity ![]() ,
, ![]() means 7 times
means 7 times ![]() , and –1|–8| means –1 times |–8|.
, and –1|–8| means –1 times |–8|.
Evaluating Algebraic Expressions
An algebraic expression is a symbolic representation of a number. It can contain constants, variables, and computation symbols. Here are examples of algebraic expressions:
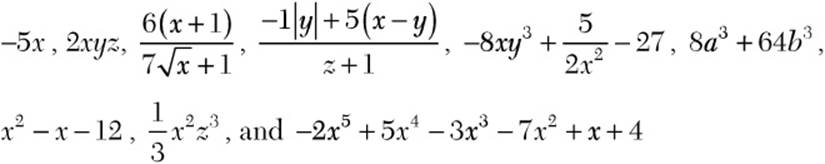
You don’t know what number an algebraic expression represents because algebraic expressions always contain variables. However, if you are given numerical values for the variables, you can evaluate the algebraic expression by substituting the given numerical value for each variable and then performing the indicated operations, being sure to follow the order of operations as you proceed. (See Chapter 4 for a discussion of order of operations.)
Problem Find the value of the algebraic expression when ![]() ,
, ![]() , and
, and ![]() .
.
a. –5x
![]()
![]()
![]()
![]()
Solution
![]()
![]() Step 1. Substitute 4 for x in the expression –5x.
Step 1. Substitute 4 for x in the expression –5x.
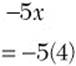
Step 2. Perform the indicated multiplication.
![]()
Step 3. State the main result.
![]()
![]()
![]() Step 1. Substitute 4 for x, –8 for y, and –5 for z in the expression 2xyz.
Step 1. Substitute 4 for x, –8 for y, and –5 for z in the expression 2xyz.
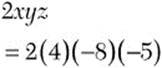
When you substitute negative values into an algebraic expression, enclose them in parentheses to avoid careless errors.
Step 2. Perform the indicated multiplication.
![]()
Step 3. State the main result.
![]()
![]()
![]() Step 1. Substitute 4 for x in the expression
Step 1. Substitute 4 for x in the expression 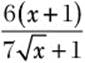 .
.
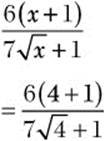
Step 2. Evaluate the resulting expression.
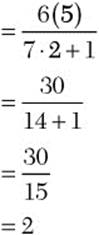
When you work with algebraic expressions, use a raised dot (·) or parentheses [()] instead of the times symbol (x) to show multiplication between numerical quantities.
Step 3. State the main result.
![]()
![]() . The square root applies only to the 4.
. The square root applies only to the 4.
![]()
![]() Step 1. Substitute 4 for x, –8 for y, and –5 for z in the expression
Step 1. Substitute 4 for x, –8 for y, and –5 for z in the expression
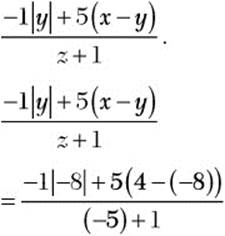
Step 2. Evaluate the resulting expression.
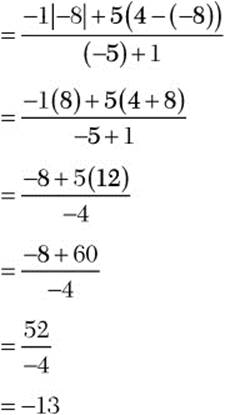
Step 3. State the main result.
![]()
![]()
![]() Step 1. Substitute 4 for x in the expression
Step 1. Substitute 4 for x in the expression ![]()
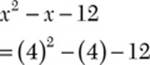
Step 2. Simplify the resulting expression.
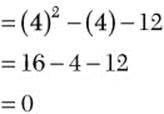
Step 3. State the main result.
![]()
Problem Evaluate ![]() when
when ![]() .
.
Solution
![]() Step 1. Substitute
Step 1. Substitute ![]() for x in the expression
for x in the expression ![]() .
.
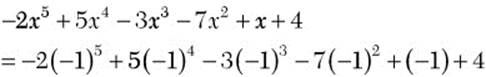
Step 2. Evaluate the resulting expression.
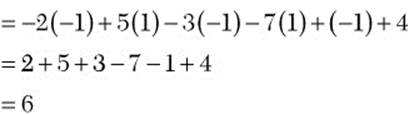
Watch your signs! It’s easy to make careless errors when you are evaluating negative numbers raised to powers.
Step 3. State the main result.
![]()
Dealing with Parentheses
Frequently, algebraic expressions are enclosed in parentheses. It is important that you deal with parentheses correctly.
![]()
If no symbol or if a + symbol immediately precedes parentheses that enclose an algebraic expression, remove the parentheses and rewrite the algebraic expression without changing any signs.
Problem Remove parentheses: ![]() .
.
Solution
![]() Step 1. Remove the parentheses without changing any signs.
Step 1. Remove the parentheses without changing any signs.
![]()
![]()
If a – symbol immediately precedes parentheses that enclose an algebraic expression, remove the parentheses and the – symbol and rewrite the algebraic expression but with all the signs changed.
Problem Remove parentheses: ![]() .
.
Solution
![]() Step 1. Remove the parentheses and the – symbol and rewrite the expression, but change all the signs.
Step 1. Remove the parentheses and the – symbol and rewrite the expression, but change all the signs.
![]()
![]() . Change all the signs, not just the first one. This mistake is very common.
. Change all the signs, not just the first one. This mistake is very common.
Problem Remove parentheses.
![]()
![]()
Solution
![]()
![]() Step 1. Remove the parentheses and rewrite the algebraic expression in parentheses without changing any signs.
Step 1. Remove the parentheses and rewrite the algebraic expression in parentheses without changing any signs.
![]()
![]()
![]() Step 1. Remove the parentheses and the – symbol and rewrite the expression in parentheses, but change all the signs.
Step 1. Remove the parentheses and the – symbol and rewrite the expression in parentheses, but change all the signs.
![]()
![]()
If a number immediately precedes (or immediately follows) parentheses that enclose an algebraic expression, apply the distributive property to remove the parentheses.
Recall that the distributive property is ![]() and
and ![]() .
.
Problem Remove parentheses.
![]()
![]()
![]()
Solution
![]()
![]() Step 1. Apply the distributive property.
Step 1. Apply the distributive property.
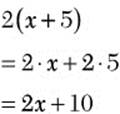
![]() . You must multiply the 5 by 2 as well.
. You must multiply the 5 by 2 as well.
![]()
![]() Step 1. Apply the distributive property.
Step 1. Apply the distributive property.
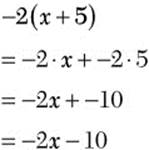
It’s always correct to change +– to simply –.
![]()
![]() Step 1. Apply the distributive property.
Step 1. Apply the distributive property.
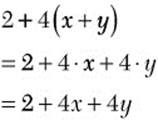
![]() because, in the order of operations, you multiply before you add.
because, in the order of operations, you multiply before you add. ![]() , but
, but ![]()
 Exercise 11
Exercise 11
1. Name the variable(s) and constant(s) in the expression 4s, where s is the measure of the side of a square.
For 2–4, state the numerical coefficient of the variable.
2. –12x
3. z
![]()
For 5–11, evaluate the algebraic expression when ![]() ,
, ![]() , and
, and ![]() .
.
![]()
![]()
![]()
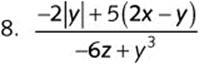
![]()
![]()
![]()
For 12–15, remove parentheses.
![]()
![]()
![]()
![]()