Easy Algebra Step-by-Step: Master High-Frequency Concepts and Skills for Algebra Proficiency—FAST! (2012)
Chapter 12. Factoring Polynomials
In this chapter, you learn about factoring polynomials.
Factoring and Its Objectives
Factoring is the process of undoing multiplication, so you need a strong understanding of multiplication of polynomials to be skillful in factoring them. You can expect that, from time to time throughout the chapter, you will be asked to recall your prior knowledge of multiplication of polynomials.
The reality that factoring polynomials requires agility in multiplying polynomials underscores the importance of mastering previous skills in mathematics before going on to new ones. Expecting to learn a new math topic that relies on previous skills that were not mastered is a self-defeating strategy that often leads to disappointing results. Some advice: Don’t make this mistake!
The objective in factoring is to take a complicated polynomial and express it as the product of simpler polynomial factors. You might ask, “Why would you want to do this?” One practical answer is that, generally, you have fewer restrictions on factors than you do on terms. Factors are joined by multiplication, but terms are joined by addition or subtraction. The following problem illustrates this point.
Problem Follow the indicated directions for the six true sentences given below. (For convenience, assume x and y are positive real numbers with x < y.)
1. ![]()
![]()
![]()
4. ![]()
5. ![]()
6. ![]()
a. From the statements of equality and inequality in sentences 1–6, list those involving terms.
b. From the statements of equality and inequality in sentences 1–6, list those involving factors and no terms.
Solution
a. From the statements of equality and inequality in sentences 1–6, list those involving terms.
![]() Step 1. Examine sentences 1–6 for equality or inequality statements involving terms and then list those involving terms.
Step 1. Examine sentences 1–6 for equality or inequality statements involving terms and then list those involving terms.
![]()
![]() (Note that the statements involving terms contain the ≠ symbol.)
(Note that the statements involving terms contain the ≠ symbol.)
b. From the statements of equality and inequality in sentences 1–6, list those involving factors and no terms.
![]() Step 1. Examine sentences 1–6 for equality or inequality statements involving terms and then list those not involving terms.
Step 1. Examine sentences 1–6 for equality or inequality statements involving terms and then list those not involving terms.
![]()
![]() (Note that the statements involving factors and no terms contain the = symbol.)
(Note that the statements involving factors and no terms contain the = symbol.)
Greatest Common Factor
The previous problem should motivate you to become proficient in factoring polynomials. The discussion begins with factoring out the greatest common monomial factor. The greatest common monomial factor is the product of the greatest common numerical factor and a second component made up of the common variable factors, each with the highest power common to each term. You can refer to the greatest common monomial factor as the greatest common factor (GCF).
Problem Find the GCF for the terms in the polynomial ![]()
Solution
![]() Step 1. Find the numerical factor of the GCF by finding the greatest common numerical factor of 12 and 8.
Step 1. Find the numerical factor of the GCF by finding the greatest common numerical factor of 12 and 8.
The factors of 12 are 1, 2, 3, 4, 6, and 12, and the factors of 8 are 1, 2, 4, and 8. The numerical factor of the GCF is 4.
Step 2. Identify the common variable factors, each with the highest power common to x8y3 and x6y7z2.
x and y are the common variable factors. The highest power of x that is common to each term is x6, and the highest power of y that is common to each term is y3. The common variable component of the GCF is x6y3.
Step 3. Write the GCF as the product of the results of steps 1 and 2.
The GCF for the terms in the polynomial ![]()
When factoring out the GCF, check your work by mentally multiplying the factors of your answers.
Problem Factor.
![]()
![]()
![]()
![]()
Solution
![]()
![]() Step 1. Determine the GCF for
Step 1. Determine the GCF for ![]() and
and ![]()
GCF = 4x6y3
Step 2. Rewrite each term of the polynomial as an equivalent product of 4x6y3 and a second factor.
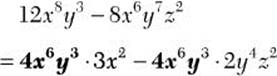
Step 3. Use the distributive property to factor 4x6y3 from the resulting expression.
![]()
![]() is not in factored form because it is not a product, but
is not in factored form because it is not a product, but ![]() is in factored form because it is the product of
is in factored form because it is the product of ![]() and
and ![]()
Step 3. Review the main steps.
![]()
![]()
![]() Step 1. Determine the GCF for 15x2 and 3x.
Step 1. Determine the GCF for 15x2 and 3x.
GCF = 3x
Step 2. Rewrite each term of the polynomial as an equivalent product of 3x and a second factor.
![]()
![]() ask yourself, “What times 3x equals 3x?” The answer is 1, not 0. Remember to mentally multiply the factors to check your work.
ask yourself, “What times 3x equals 3x?” The answer is 1, not 0. Remember to mentally multiply the factors to check your work.
Step 3. Use the distributive property to factor 3x from the resulting expression.
![]()
Step 4. Review the main steps.
![]()
![]()
![]() Step 1. Determine the GCF for x3y, xy, and y.
Step 1. Determine the GCF for x3y, xy, and y.
GCF = y
Step 2. Rewrite each term of the polynomial as an equivalent product of y and a second factor.
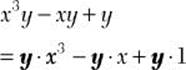
Step 3. Use the distributive property to factor y from the resulting expression.
![]()
Step 4. Review the main steps.
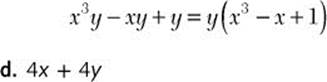
![]() Don’t forget the 1.
Don’t forget the 1.
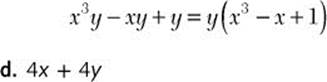
![]() Step 1. Use the distributive property to factor 4 from the polynomial.
Step 1. Use the distributive property to factor 4 from the polynomial.
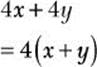
GCF with a Negative Coefficient
At times, you might need to factor out a GCF that has a negative coefficient. To avoid sign errors, mentally change subtraction to add the opposite.
Problem Factor using a negative coefficient for the GCF.
![]()
![]()
![]()
![]()
When factoring out a GCF that has a negative coefficient, always mentally multiply the factors and check the signs.
Solution
![]()
![]() Step 1. Determine the GCF with a negative coefficient for –5xy2 and 10xy.
Step 1. Determine the GCF with a negative coefficient for –5xy2 and 10xy.
GCF = –5xy
Step 2. Rewrite each term of the polynomial as an equivalent product of –5xy and a second factor.
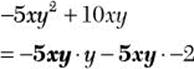
Step 3. Use the distributive property to factor –5xy from the resulting expression.
![]()
Step 4. Review the main steps.
![]()
![]() Check the signs!
Check the signs!
![]()
![]() Step 1. Determine the GCF with a negative coefficient for –5xy2 and 10xy.
Step 1. Determine the GCF with a negative coefficient for –5xy2 and 10xy.
GCF = –5xy
Step 2. Rewrite each term of the polynomial as an equivalent product of –5xy and a second factor.
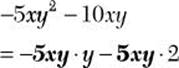
Step 3. Use the distributive property to factor –5xy from the resulting expression.
![]()
To avoid sign errors, it is often helpful to mentally change a minus symbol to “+ –.”
Step 4. Review the main steps.
![]()
![]()
![]() Step 1. Insert the understood coefficients of 1.
Step 1. Insert the understood coefficients of 1.
![]()
Step 2. Use the distributive property to factor –1 from the polynomial.
![]()
Step 3. Review the main steps.
![]()
![]()
![]() Step 1. Determine the GCF with a negative coefficient for –2x3, 4x, and –8.
Step 1. Determine the GCF with a negative coefficient for –2x3, 4x, and –8.
GCF = –2
Step 2. Rewrite each term of the polynomial as an equivalent product of –2 and a second factor.
–2x3 + 4x – 8
![]()
Step 3. Use the distributive property to factor –2 from the resulting expression.
![]()
Step 4. Review the main steps.
![]()
A Quantity as a Common Factor
You might have a common quantity as a factor in the GCF.
Problem Factor.
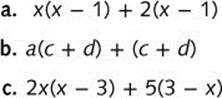
Solution
![]()
![]() Step 1. Determine the GCF for x(x – 1) and 2(x – 1).
Step 1. Determine the GCF for x(x – 1) and 2(x – 1).
GCF = (x – 1)
Step 2. Use the distributive property to factor (x – 1) from the expression.
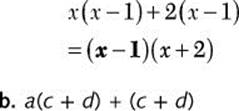
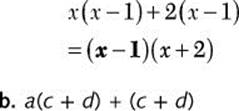
![]() Step 1. Determine the GCF for a(c + d) and (c + d).
Step 1. Determine the GCF for a(c + d) and (c + d).
GCF = (c + d)
Step 2. Use the distributive property to factor (c + d) from the expression.
a(c+d)+(c+d)
![]()
![]() Don’t leave off the 1. Think of (c + d) as 1(c + d).
Don’t leave off the 1. Think of (c + d) as 1(c + d).
![]()
![]() Step 1. Because
Step 1. Because ![]() , factor –1 from the second term.
, factor –1 from the second term.
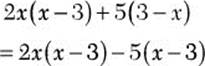
Step 2. Determine the GCF for 2x(x – 3) and 5(x – 3).
GCF = (x – 3)
Step 3. Use the distributive property to factor (x – 3) from the expression.
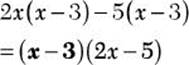
Factoring Four Terms
When you have four terms to factor, grouping the terms in pairs might yield a quantity as a common factor.
Problem Factor by grouping in pairs.
![]()
![]()
Solution
![]()
![]() Step 1. Group the terms in pairs that will yield a common factor.
Step 1. Group the terms in pairs that will yield a common factor.
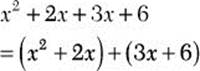
Step 2. Factor the common factor x out of the first term and the common factor 3 out of the second term.
![]()
![]() These quantities are terms, not factors.
These quantities are terms, not factors.
Step 3. Determine the GCF for x(x + 2) and 3(x + 2).
GCF = (x + 2)
Step 4. Use the distributive property to factor (x + 2) from the expression.
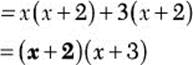
![]()
![]() Step 1. Rearrange the terms so that the first two terms have a common factor and the last two terms have a common factor, and then group the terms in pairs accordingly.
Step 1. Rearrange the terms so that the first two terms have a common factor and the last two terms have a common factor, and then group the terms in pairs accordingly.
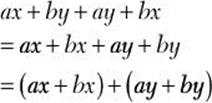
Step 2. Factor the common factor x out of the first term and the common factor y out of the second term.
![]()
Step 3. Determine the GCF for x(a + b) and y(a + b).
GCF = (a + b)
Step 4. Use the distributive property to factor (a + b) from the expression.
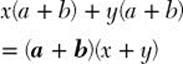
Factoring Quadratic Trinomials
When you have three terms to factor, you might have a quadratic trinomial of the form ![]() It turns out that not all quadratic trinomials are factorable using real number coefficients, but many will factor. Those that do will factor as the product of two binomials.
It turns out that not all quadratic trinomials are factorable using real number coefficients, but many will factor. Those that do will factor as the product of two binomials.
You should recall (from Chapter 9) that quadratic trinomials result when you multiply two binomials.
Two common methods for factoring ![]() are factoring by trial and error and factoring by grouping.
are factoring by trial and error and factoring by grouping.
Factoring by Trial and Error Using FOIL
When you factor by trial and error, it is very helpful to call to mind the FOIL method of multiplying two binomials. Here is an example.
(2x + 5)(3x + 4)
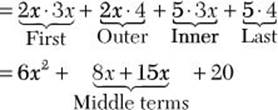
= ![]()
Your task when factoring 6x2 + 23x + 20 is to reverse the FOIL process to obtain ![]() in factored form. As you work through the problems, you will find it useful to know the following: If the first and last terms of a factorable quadratic trinomial are positive, the signs of the second terms in the two binomial factors of the trinomial have the same sign as the middle term of the trinomial.
in factored form. As you work through the problems, you will find it useful to know the following: If the first and last terms of a factorable quadratic trinomial are positive, the signs of the second terms in the two binomial factors of the trinomial have the same sign as the middle term of the trinomial.
Problem Factor by trial and error.
![]()
![]()
![]()
![]()
![]()
![]()
Solution
![]()
![]() Step 1. Because the expression has the form
Step 1. Because the expression has the form ![]() , look for two binomial factors.
, look for two binomial factors.
![]()
Step 2. x2 is the first term, so the first terms in the two binomial factors must be x.
![]()
Step 3. –14 is the last term, and it is positive, so the last terms in the two binomial factors have the same sign as 9, with a product of 14 and a sum of 9. Try 7 and 2 and check with FOIL.
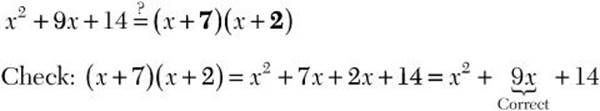
Step 4. Write the factored form.
![]()
![]()
![]() Step 1. Because the expression has the form
Step 1. Because the expression has the form ![]() look for two binomial factors.
look for two binomial factors.
![]()
Step 2. x2 is the first term, so the first terms in the two binomial factors must be x.
![]()
Step 3. 14 is the last term, and it is positive, so the last terms in the two binomial factors have the same sign as –9, with a product of 14 and a sum of –9. Try –7 and –2 and check with FOIL.
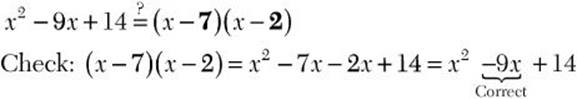
Step 4. Write the factored form.
![]()
![]()
![]() Step 1. Because the expression has the form
Step 1. Because the expression has the form ![]() look for two binomial factors.
look for two binomial factors.
![]()
Step 2. x2 is the first term, so the first terms in the two binomial factors must be x.
![]()
Step 3. –14 is the last term, and it is negative, so the last terms in the two binomial factors have opposite signs with a product of –14 and a sum of 5. Try combinations of factors of –14 and check with FOIL.
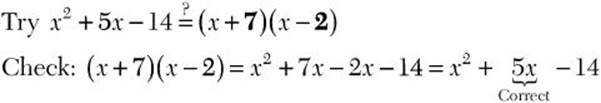
Step 4. Write the factored form.
![]()
![]()
![]() Step 1. Because the expression has the form
Step 1. Because the expression has the form ![]() look for two binomial factors.
look for two binomial factors.
![]()
Step 2. x2 is the first term, so the first terms in the two binomial factors must be x.
![]()
Step 3. –14 is the last term, and it is negative, so the last terms in the two binomial factors have opposite signs with a product of –14 and a sum of –5. Try combinations of factors of –14 and check with FOIL.
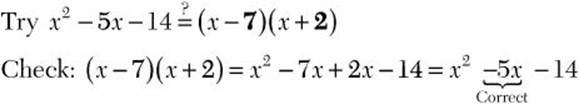
Step 4. Write the factored form.
![]()
![]()
![]() Step 1. Because the expression has the form
Step 1. Because the expression has the form ![]() look for two binomial factors.
look for two binomial factors.
![]()
Step 2. 3x2 is the first term, so the first terms in the two binomial factors must be 3x and x.
![]()
Step 3. –2 is the last term, and it is negative, so the last terms in the two binomial factors have opposite signs with a product of –2. Try combinations using the factors of –2 and check with FOIL until the middle term is correct.
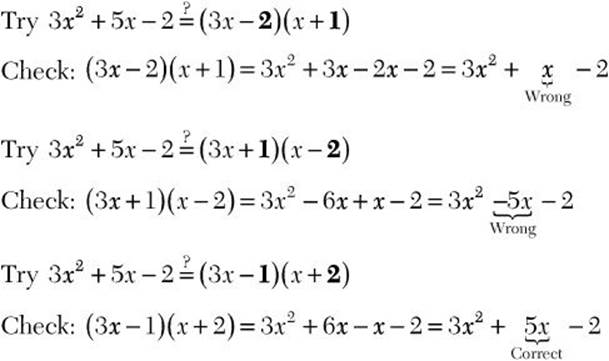
Step 4. Write the factored form.
![]()
![]()
![]() Step 1. Because the expression has the form
Step 1. Because the expression has the form ![]() look for two binomial factors.
look for two binomial factors.
![]()
Step 2. 4x2 is the first term, so the numerical coefficients of the first terms in the two binomial factors are factors of 4. The last term is –3, so the last terms of the two binomial factors have opposite signs with a product of –3. Try combinations of factors of 4 and –3 and check with FOIL until the middle term is correct.
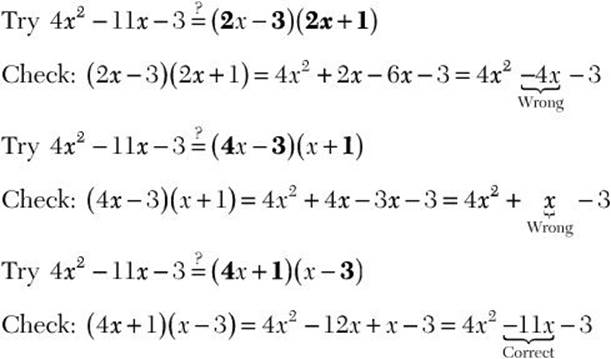
Step 3. Write the factored form.
![]()
As you can see, getting the middle term right is the key to a successful factorization of ![]() You can shorten your checking time by simply using FOIL to compare the sum of the inner and outer products to the middle term of the trinomial.
You can shorten your checking time by simply using FOIL to compare the sum of the inner and outer products to the middle term of the trinomial.
Factoring by Grouping
When you factor ![]() by grouping, you also guess and check, but in a different way than in the previous method.
by grouping, you also guess and check, but in a different way than in the previous method.
Problem Factor by grouping.
![]()
![]()
Solution
![]()
![]() Step 1. Identify the coefficients a, b, and c and then find two factors of ac whose sum is b.
Step 1. Identify the coefficients a, b, and c and then find two factors of ac whose sum is b.
When you’re identifying coefficients for ax2 + bx + c, keep a – symbol with the number that follows it.
![]()
Two factors of –12 that sum to –11 are –12 and 1.
Step 2. Rewrite ![]() replacing the middle term, –11x, with
replacing the middle term, –11x, with ![]()
![]()
Step 3. Group the terms in pairs that will yield a common factor.
![]()
Step 4. Factor the common factor 4x out of the first term and simplify the second term.
![]()
Step 5. Use the distributive property to factor (x – 3) from the expression.
![]()
Step 6. Write the factored form.
![]()
![]()
![]() Step 1. Identify the coefficients a, b, and c and then find two factors of ac whose sum is b.
Step 1. Identify the coefficients a, b, and c and then find two factors of ac whose sum is b.
a = 9, b = –12, and c = 4
ac = 9 · 4 = 36
Two factors of 36 that sum to –12 are –6 and –6.
Step 2. Rewrite ![]() replacing the middle term, –12x, with –6x – 6x.
replacing the middle term, –12x, with –6x – 6x.
![]()
Step 3. Group the terms in pairs that will yield a common factor.
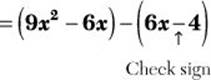
Step 4. Factor the common factor 3x out of the first term and the common factor 2 out of the second term.
![]()
Step 5. Use the distributive property to factor (3x – 2) from the expression.
![]()
Step 6. Write the factored form.
![]()
Perfect Trinomial Squares
The trinomial ![]() which equals
which equals ![]() is a perfect trinomial square. If you recognize that
is a perfect trinomial square. If you recognize that ![]() is a perfect trinomial square, then you can factor it rather quickly. A trinomial is a perfect square if a and c are both positive and
is a perfect trinomial square, then you can factor it rather quickly. A trinomial is a perfect square if a and c are both positive and ![]() . The following problem illustrates the procedure.
. The following problem illustrates the procedure.
Problem Factor.
![]()
![]()
Solution
![]()
![]() Step 1. Identify the coefficients a, b, and c and check whether
Step 1. Identify the coefficients a, b, and c and check whether ![]()
a= 4, b= –20, and c= 25
![]()
Thus, ![]() is a perfect trinomial square.
is a perfect trinomial square.
Step 2. Indicate that ![]() will factor as the square of a binomial.
will factor as the square of a binomial.
![]()
Step 3. Fill in the binomial. The first term is the square root of 4x2 and the last term is the square root of 25. The sign in the middle is the same as the sign of the middle term of the trinomial.
![]() is the factored form.
is the factored form.
![]()
![]() Step 1. Identify the coefficients a, b, and c and check whether
Step 1. Identify the coefficients a, b, and c and check whether ![]()
a= 1, b= 6, and c= 9
![]()
Thus, ![]() is a perfect trinomial square.
is a perfect trinomial square.
Step 2. Indicate that ![]() will factor as the square of a binomial.
will factor as the square of a binomial.
![]()
Step 3. Fill in the binomial. The first term is the square root of x2 and the last term is the square root of 9. The sign in the middle is the same as the sign of the middle term of the trinomial.
![]() is the factored form.
is the factored form.
Factoring Two Terms
When you have two terms to factor, consider these special binomial products from Chapter 9: the difference of two squares, the difference of two cubes, and the sum of two cubes.
The difference of two squares has the form x2 – y2 (quantity squared minus quantity squared). You factor the difference of two squares like this:
x2 + y2, the sum of two squares, is not factorable (over the real numbers).
![]()
The difference of two cubes has the form x3 – y3 (quantity cubed minus quantity cubed). You factor the difference of two cubes like this:
![]()
The sum of two cubes has the form x3 + y3 (quantity cubed plus quantity cubed). You factor the sum of two cubes like this:
![]()
Problem Factor.
![]()
![]()
![]()
![]()
![]()
Solution
![]()
![]() Step 1. Observe that the binomial has the form “quantity squared minus quantity squared,” so it is the difference of two squares. Indicate that
Step 1. Observe that the binomial has the form “quantity squared minus quantity squared,” so it is the difference of two squares. Indicate that ![]() factors as the product of two binomials, one with a plus sign between the terms and the other with a minus sign between the terms.
factors as the product of two binomials, one with a plus sign between the terms and the other with a minus sign between the terms.
![]()
Step 2. Fill in the terms of the binomials. The two first terms are the same, and they both equal ![]() . The two last terms are the same, and they both equal
. The two last terms are the same, and they both equal ![]()
![]()
![]()
![]() Step 1. Observe that the binomial has the form “quantity squared minus quantity squared,” so it is the difference of two squares. Indicate that x2 – 1 factors as the product of two binomials, one with a plus sign between the terms and the other with a minus sign between the terms.
Step 1. Observe that the binomial has the form “quantity squared minus quantity squared,” so it is the difference of two squares. Indicate that x2 – 1 factors as the product of two binomials, one with a plus sign between the terms and the other with a minus sign between the terms.
![]()
Step 2. Fill in the terms of the binomials. The two first terms are the same, and they both equal ![]() . The two last terms are the same, and they both equal
. The two last terms are the same, and they both equal ![]() .
.
![]() is the factored form.
is the factored form.
![]()
![]() Step 1. Observe that the binomial has the form “quantity squared plus quantity squared,” so it is the sum of two squares, and thus is not factorable over the real numbers.
Step 1. Observe that the binomial has the form “quantity squared plus quantity squared,” so it is the sum of two squares, and thus is not factorable over the real numbers.
![]()
![]()
![]() Step 1. Observe that the binomial has the form “quantity cubed minus quantity cubed,” so it is the difference of two cubes. Indicate that 8x3 – 27 factors as the product of a binomial and a trinomial. The binomial has a minus sign between the terms, and the trinomial has plus signs between the terms.
Step 1. Observe that the binomial has the form “quantity cubed minus quantity cubed,” so it is the difference of two cubes. Indicate that 8x3 – 27 factors as the product of a binomial and a trinomial. The binomial has a minus sign between the terms, and the trinomial has plus signs between the terms.
![]()
Step 2. Fill in the terms of the binomial. The first term is ![]() , and the second term is
, and the second term is ![]()
![]()
Step 3. Fill in the terms of the trinomial by using the terms of the binomial, 2x and 3, to obtain the terms. The first term is (2x)2 = 4x2, the second term is 2x · 3 = 6x, and the third term is 32 = 9.
![]() is the factored form.
is the factored form.
![]()
![]()
![]() Step 1. Observe that the binomial has the form “quantity cubed plus quantity cubed,” so it is the sum of two cubes. Indicate that
Step 1. Observe that the binomial has the form “quantity cubed plus quantity cubed,” so it is the sum of two cubes. Indicate that ![]() factors as the product of a binomial and a trinomial. The binomial has a plus sign between the terms, and the trinomial has one minus sign on the middle term.
factors as the product of a binomial and a trinomial. The binomial has a plus sign between the terms, and the trinomial has one minus sign on the middle term.
![]()
Step 2. Fill in the terms of the binomial. The first term is ![]() and the second term is
and the second term is ![]() .
.
![]()
Step 3. Fill in the terms of the trinomial by using the terms of the binomial, 4a and 5, to obtain the terms. The first term is (4a)2 = 16a2, the second term is 4a · 5 = 20a, and the third term is 52 = 25.
![]()
Guidelines for Factoring
Finally, here are some general guidelines for factoring of polynomials.
1. Count the number of terms.
2. If the expression has a GCF, factor out the GCF.
3. If there are two terms, check for a special binomial product.
4. If there are three terms, check for a quadratic trinomial.
5. If there are four terms, try grouping in pairs.
6. Check whether any previously obtained factor can be factored further.
Problem Factor completely.
![]()
![]()
Solution
![]()
![]() Step 1. Factor out the GCF, 25x2y2z.
Step 1. Factor out the GCF, 25x2y2z.
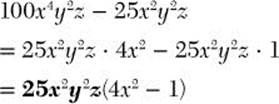
Step 2. Factor the difference of two squares, 4x2 – 1.
![]() is the completely factored form.
is the completely factored form.
![]()
Step 1. Factor out the GCF, (x + y).
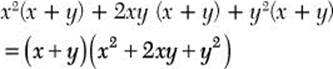
Step 2. Factor the perfect trinomial square, ![]() and simplify.
and simplify. ![]() is the completely factored form.
is the completely factored form.
![]() Exercise 12
Exercise 12
In 1–5, indicate whether the statement is true or false.
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
For 6–8, factor using a negative coefficient for the GCF.
![]()
![]()
![]()
For 9–24, factor completely.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()