Easy Algebra Step-by-Step: Master High-Frequency Concepts and Skills for Algebra Proficiency—FAST! (2012)
Chapter 5. Order of Operations
In this chapter, you apply your skills in computation to perform a series of indicated numerical operations. This chapter lays the foundation for numerical calculations by introducing you to the order of operations.
Grouping Symbols
Grouping symbols such as parentheses ( ), brackets [ ], and braces { } are used to keep things together that belong together.
Do keep in mind that parentheses are also used to indicate multiplication, as in (–5)(–8) or for clarity, as in –(–35).
Fraction bars, absolute value bars | |, and square root symbols 
are also grouping symbols. When you are performing computations, perform operations in grouping symbols first.
Grouping symbols say “Do me first!”
It is very important that you do so when you have addition or subtraction inside the grouping symbol.
Problem Simplify.
a. (1 + 1)4
b. 
c. 
d. |8 + –5|
e. 
Solution
a. (1 + 1)4
When you no longer need the grouping symbol, omit it.
Step 1. Parentheses are a grouping symbol, so do 1 + 1 first.
(1 + 1)4 = 24
Step 2. Evaluate 24.
= 16
b. 
(1 + 1)4 ≠ 14 + 14 · (1 + 1)4 = 16, but 14 + 14 = 1 + 1 = 2. Not performing the addition, 1 + 1, inside the parentheses first can lead to an incorrect result.
Step 1. The fraction bar is a grouping symbol, so do the addition, 4 + 10, over the fraction bar first.
Step 2. Simplify 
.
c. 
. Not performing the addition, 4 + 10, first can lead to an incorrect result.
Step 1. The fraction bar is a grouping symbol, so do the addition, –7 + 25, over the fraction bar and the subtraction, 3 – 5, under the fraction bar first.
Step 2. Compute 
.
= –9
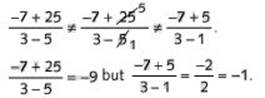
Not performing the addition, –7 + 25, and the subtraction, 3 – 5, first can lead to an incorrect result.
d. |8 + –15|
Step 1. Absolute value bars are a grouping symbol, so do 8 + –15 first.
|8 + –15| = |–7|
Step 2. Evaluate |–7|.
= 7
|8 + –15| ≠ |8| + |–15| · |8 + –15| = 7, but |8| + |–15| = 8+15 = 23. Not performing the addition, 8 + –15, first can lead to an incorrect result.
e. 
Step 1. The square root symbol is a grouping symbol, so do 36 + 64 first.
Step 2. Evaluate 
.
= 10
, 
. Not performing the addition, 36 + 64, first can lead to an incorrect result.
PEMDAS
You must follow the order of operations to simplify mathematical expressions. Use the mnemonic “Please Excuse My Dear Aunt Sally”—abbreviated as PE(MD)(AS) to help you remember the following order.
Order of Operations
1. Do computations inside Parentheses (or other grouping symbols).
2. Evaluate Exponential expressions (also, evaluate absolute value, square root, and other root expressions).
3. Perform Multiplication and Division, in the order in which these operations occur from left to right.
4. Perform Addition and Subtraction, in the order in which these operations occur from left to right.
In the order of operations, multiplication does not always have to be done before division, or addition before subtraction. You multiply and divide in the order they occur in the problem. Similarly, you add and subtract in the order they occur in the problem.
Problem Simplify.
a. 
b. 100 + 8 · 32 – 63 ÷ (2 + 5)
c. 
Solution
a. 
Step 1. Compute 1 + 1 inside the parentheses.
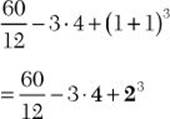
Step 2. Evaluate 23.
Step 3. Compute 
.
= 5 – 3 · 4 + 8
5 – 3 · 4 + 8 ≠ 2 · 12. Multiply before adding or subtractin—when no grouping symbols are present.
Step 4. Compute 3 · 4.
= 5 – 12 + 8
Step 5. Compute 5 – 12.
= –7 + 8
Step 6. Compute –7 + 8.
= 1
Step 7. Review the main steps.
b. 100 + 8 · 32 – 63 ÷ (2 + 5)
8 · 32 ≠ 242. 8 · 32 = 8 · 9 = 72, but 242 = 576. Do exponentiation before multiplication.
Step 1. Compute 2 + 5 inside the parentheses.
100 + 8 · 32 – 63 ÷ (2 + 5)
= 100 + 8 · 32 – 63 ÷ 7
100 + 8 · 9 ≠ 108 · 9. Do multiplication before addition (except when a grouping symbol indicates otherwise).
Step 2. Evaluate 32.
= 100 + 8 · 9 – 63 ÷ 7
Step 3. Compute 8 · 9.
= 100 + 72 – 63 ÷ 7
Step 4. Compute 63 ÷ 7.
= 100 + 72 – 9
72 – 63 ÷ 7 ≠ 9 ÷ 7. Do division before subtraction (except when a grouping symbol indicates otherwise).
Step 5. Compute 100 + 72.
= 172 – 9
Step 6. Compute 172 – 9.
= 163
Step 7. Review the main steps.
100 + 8 · 32 – 63 ÷ (2 + 5) = 100 + 8 · 32 – 63 ÷ 7 = 100 + 8 · 9 – 63 ÷ 7
= 100 + 72 – 9 = 163
c. 
Step 1. Compute quantities in grouping symbols.
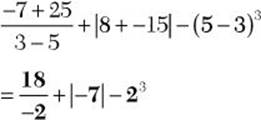
Step 2. Evaluate |–7| and 23.
Evaluate absolute value expressions before multiplication or division.
Step 3. Compute 
.
= –9 + 7 – 8
Step 4. Compute –9 + 7.
= –2 – 8
Step 5. Compute –2 – 8.
= –10
Step 6. Review the main steps.
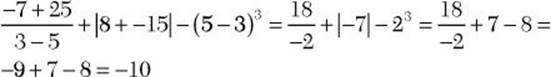
Exercise 5
Simplify.
1. (5 + 7)6 – 10
2. (–72)(6 – 8)
3. (2 – 3)(–20)
4. 
5. 
6. –22 · –3 – (15 – 4)2
7. 5(11 – 3 – 6 · 2)2
8. 
9. 
10. 
11. 
12. (12 – 5) – (5 – 12)
13. 
14. –8 + 2(–1)2 + 6
15. 