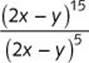Easy Algebra Step-by-Step: Master High-Frequency Concepts and Skills for Algebra Proficiency—FAST! (2012)
Chapter 7. Rules for Exponents
In Chapter 4, you learned about the various types of exponents that you might encounter in algebra. In this chapter, you learn about the rules for exponents—which you will find useful when you simplify algebraic expressions. The following rules hold for all real numbers x and y and all rational numbers m, n, and p, provided that all indicated powers are real and no denominator is 0.
Product Rule
![]() Product Rule for Exponential Expressions with the Same Base
Product Rule for Exponential Expressions with the Same Base
xm xn = xm+n
This rule tells you that when you multiply exponential expressions that have the same base, you add the exponents and keep the same base.
If the bases are not the same, don’t use the product rule for exponential expressions with the same base.
Problem Simplify.
a. x2 x3
b. x2 y5
c. x2 x7 y3 y5
Solution
a. x2 x3
![]() Step 1. Check for exponential expressions that have the same base.
Step 1. Check for exponential expressions that have the same base.
x2 x3
x2 and x3 have the same base, namely, x.
Step 2. Simplify x2 x3. Keep the base x and add the exponents 2 and 3.
x2 x3 = x2+3 = x5
x2x3 ≠ x2.3 = x6 When multiplying, add the exponents of the same base, don’t multiply them.
b. x2y5
![]() Step 1. Check for exponential expressions that have the same base.
Step 1. Check for exponential expressions that have the same base.
x2y5
x2 and y5 do not have the same base, so the product cannot be simplified.
x2y5 ≠ (xy)7. This is a common error that you should avoid.
c. x2x7y3y5
![]() Step 1. Check for exponential expressions that have the same base.
Step 1. Check for exponential expressions that have the same base.
x2x7y3y5
x2 and x7 have the same base, namely, x, and y3 and y5 have the same base, namely, y.
Step 2. Simplify x2x7 and y3y5 For each, keep the base and add the exponents.
x2x7y3y5 = x2+7y3+5 = x9y8
Quotient Rule
![]() Quotient Rule for Exponential Expressions with the Same Base
Quotient Rule for Exponential Expressions with the Same Base
![]()
This rule tells you that when you divide exponential expressions that have the same base, you subtract the denominator exponent from the numerator exponent and keep the same base.
If the bases are not the same, don’t use the quotient rule for exponential expressions with the same base.
Problem Simplify.
a. ![]()
b. ![]()
c. ![]()
d. ![]()
Solution
a. ![]()
![]() Step 1. Check for exponential expressions that have the same base.
Step 1. Check for exponential expressions that have the same base.
![]()
x5 and x3 have the same base, namely, x.
Step 2. Simplify ![]() . Keep the base x and subtract the exponents 5 and 3.
. Keep the base x and subtract the exponents 5 and 3.
![]()
![]() . When dividing, subtract the exponents of the same base, don’t divide them.
. When dividing, subtract the exponents of the same base, don’t divide them.
b. ![]()
![]() Step 1. Check for exponential expressions that have the same base.
Step 1. Check for exponential expressions that have the same base.
![]()
y5 and x2 do not have the same base, so the quotient cannot be simplified.
![]() . This is a common error that you should avoid.
. This is a common error that you should avoid.
C. ![]()
![]() Step 1. Check for exponential expressions that have the same base.
Step 1. Check for exponential expressions that have the same base.
![]()
x7 and x2 have the same base, namely, x, and y5 and y3 have the same base, namely, y.
Step 2. Simplify ![]() and
and ![]() For each, keep the base and subtract the exponents.
For each, keep the base and subtract the exponents.
![]()
d. ![]()
![]() Step 1. Check for exponential expressions that have the same base.
Step 1. Check for exponential expressions that have the same base.
![]()
x3 and x10 have the same base, namely, x.
Step 2. Simplify ![]() Keep the base x and subtract the exponents 3 and 10.
Keep the base x and subtract the exponents 3 and 10.
![]()
Step 3. Express x–7 as an equivalent exponential expression with a positive exponent.
![]()
When you simplify expressions, make sure your final answer does not contain negative exponents.
Rules for Powers
![]() Rule for a Power to a Power
Rule for a Power to a Power
(xm)p = xmp
This rule tells you that when you raise an exponential expression to a power, keep the base and multiply exponents.
Problem Simplify.
a. (x2)3
b. (y3)5
Solution
a. (x2)3
![]() Step 1. Keep the same base x and multiply the exponents 2 and 3.
Step 1. Keep the same base x and multiply the exponents 2 and 3.
(x2)3 = x2.3 = x6
(x2)3 ≠ x5. For a power to a power, multiply exponents, don’t add.
b. (y3)5
![]() Step 1. Keep the same base y and multiply the exponents 3 and 5.
Step 1. Keep the same base y and multiply the exponents 3 and 5.
(y3)5 = y3.5 = 1515
![]() Rule for the Power of a Product
Rule for the Power of a Product
(xy)p = ypyp
This rule tells you that a product raised to a power is the product of each factor raised to the power.
Confusing the rule (xy)p = xpyp with the rule xmxn = xm+n is a common error. Notice that the rule (xy)p = xpyp has the same exponent and different bases, while the rule xmxn = xm+n has the same base and different exponents.
Problem Simplify.
a. (xy)6
b. (4x)3
c. (x3y2z)4
Solution
a. (xy)6
![]() Step 1. Raise each factor to the power of 6.
Step 1. Raise each factor to the power of 6.
(xy)6 = x6x6
b. (4x)3
![]() Step 1. Raise each factor to the power of 3.
Step 1. Raise each factor to the power of 3.
(4x)3 = 43x3 = 64x3
c. (x3y2z4)
![]() Step 1. Raise each factor to the power of 4.
Step 1. Raise each factor to the power of 4.
(x3y2z4 = (x)3)4(y)2)4(z)4 = x12y8z4
![]() Rule for the Power of a Quotient
Rule for the Power of a Quotient
![]()
This rule tells you that a quotient raised to a power is the quotient of each factor raised to the power.
Problem Simplify.
a. ![]()
b. 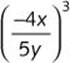
Solution
a. ![]()
![]() Step 1. Raise each factor to the power of 4.
Step 1. Raise each factor to the power of 4.
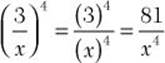
b. ![]()
![]() Step 1. Raise each factor to the power of 3.
Step 1. Raise each factor to the power of 3.
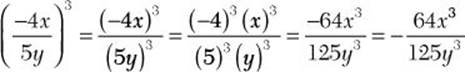
Rules for Exponents Summary
You must be very careful when simplifying using rules for exponents. For your convenience, here is a summary of the rules.
![]() Rules for Exponents
Rules for Exponents
1. Product Rule for Exponential Expressions with the Same Base
xmxn = xm+n
2. Quotient Rule for Exponential Expressions with the Same Base
![]()
3. Rule for a Power to a Power
(xm)p = xmp
4. Rule for the Power of a Product
(xy)p = xpyp
5. Rule for the Power of a Quotient
![]()
Notice there is no rule for the power of a sum [e.g., (x + y)2] or for the power of a difference [e.g., (x – y)2]. Therefore, an algebraic sum or difference raised to a power cannot be simplified using only rules for exponents.
Problem Simplify using only rules for exponents.
a. (xy)2
b. (x + y)2
c. (x – y)2
d. (x + y)2(x + y)3
e. 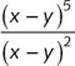
Solution
a. (xy)2
![]() Step 1. This is a power of a product, so square each factor.
Step 1. This is a power of a product, so square each factor.
xy2 = x2y2
b. (x + y)2
![]() Step 1. This is a power of a sum. It cannot be simplified using only rules for exponents.
Step 1. This is a power of a sum. It cannot be simplified using only rules for exponents.
(x + y)2 is the answer.
(x + y)2 ≠x2+y2!(x + y)2 = (x + y)(x + y) = x2 + 2xy + y2 (which you will learn in Chapter 9). This is the most common error that beginning algebra students make.
c. (x – y)2
(x – y)2 ≠ x2-y2!
![]() Step 1. This is a power of a difference. It cannot be simplified using only rules for exponents.
Step 1. This is a power of a difference. It cannot be simplified using only rules for exponents.
(x – y)2 is the answer.
d. (x + y)2(x + y)3
![]() Step 1. This is a product of expressions with the same base, namely, (x + y). Keep the base and add the exponents.
Step 1. This is a product of expressions with the same base, namely, (x + y). Keep the base and add the exponents.
(x + y)2(x + y)3 = (x + y)2+3 = (x + y)5
When a quantity enclosed in a grouping symbol acts as a base, you can use the rules for exponents to simplify as long as you continue to treat the quantity as a base.
Step 2. (x + y)5 is a power of a sum. It cannot be simplified using only rules for exponents.
(x + y)5 is the answer.
e. 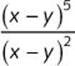
![]() Step 1. This is a quotient of expressions with the same base, namely, (x – y). Keep the base and subtract the exponents.
Step 1. This is a quotient of expressions with the same base, namely, (x – y). Keep the base and subtract the exponents.
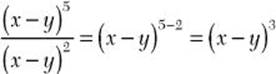
Step 2. (x – y)3 is a power of a difference. It cannot be simplified using only rules for exponents.
(x – y)3 is the answer.
![]() Exercise 7
Exercise 7
Simplify using only rules for exponents.
1. x4x9
2. x3x4y6y5
3. ![]()
4. ![]()
5. ![]()
6. (x2)5
7. (xy)5
8. (– 5x)5
9. (2x5yz3)4
10. ![]()
11. ![]()
12. (2x + 1)2
13. (3x – 5)3
14. (x + 3)(x + 3)2
15.