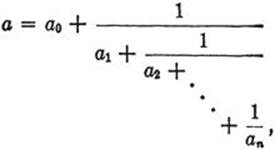What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

§4. THE EUCLIDEAN ALGORITHM

1. General Theory

The reader is familiar with the ordinary process of long division of one integer a by another integer b and knows that the process can be carried out until the remainder is smaller than the divisor. Thus if a = 648 and b= 7 we have a quotient q = 92 and a remainder r = 4.

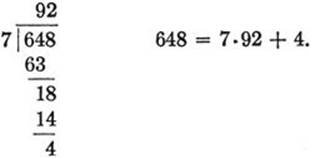
We may state this as a general theorem: If a is any integer and b is any integer greater than 0, then we can always find an integer q such that

where r is an integer satisfying the inequality 0 ≤ r < b.

To prove this statement without making use of the process of long division we need only observe that any integer a is either itself a multiple of b,

a = bq,

or lies between two successive multiples of b,

bq < a < b(q + 1) = bq + b.

In the first case the equation (1) holds with r = 0. In the second case we have, from the first of the inequalities above,

a – bq = r > 0,

while from the second inequality we have

a – bq = r < b,

so that 0 < r < b as required by (1).

From this simple fact we shall deduce a variety of important consequences. The first of these is a method for finding the greatest common divisor of two integers.

Let a and b be any two integers, not both equal to 0, and consider the set of all positive integers which divide both a and b. This set is certainly finite, since if a, for example, is ≠ 0, then no integer greater in magnitude than a can be a divisor of a, to say nothing of b. Hence there can be but a finite number of common divisors of a and b, and of these let d be the greatest. The integer d is called the greatest common divisor of a and b, and written d = (a, b). Thus for a = 8 and b = 12 we find by direct trial that (8, 12) = 4, while for a = 5 and b = 9 we find that (5, 9) = 1. When aand b are large, say a = 1804 and b = 328, the attempt to find (a. b) bv trial and error would be quite wearisome.

A short and certain method is provided by the Euclidean algorithm. (An algorithm is a systematic method for computation.) It is based on the fact that from any relation of the form

it follows that

For any number u which divides both a and b,

a = su, b = tu,

also divides r, since r = a – bq = su – qtu= (s – qt)u; and conversely, every number υ which divides b and r,

b – s′v, r = t′v,

also divides a, since a = bq + r = s′vq + t′v = (s′q + t′)v. Hence every common divisor of a and b is at the same time a common divisor of b and r, and conversely. Since, therefore, the set of all common divisors of a and b is identical with the set of all common divisors of b and r, the greatestcommon divisor of a and b must be equal to the greatest common divisor of b and r, which establishes (3). The usefulness of this relation will be seen immediately.

Let us return to the question of finding the greatest common divisor of 1804 and 328. By ordinary long division

we find that

1804 = 5·328 + 164.

Hence from (3) we conclude that

(1804, 328) = (328, 164).

Observe that the problem of finding (1804, 328) has been replaced by a problem involving smaller numbers. We may continue the process. Since

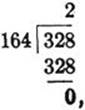
we have 328 = 2·164 + 0, so that (328, 164) = (164, 0) = 164. Hence (1804, 328) = (328, 164) = (164, 0) = 164, which is the desired result.

This process for finding the greatest common divisor of two numbers is given in a geometric form in Euclid’s Elements. For arbitrary integers a and b, not both 0, it may be described arithmetically in the following terms.

We may suppose that b ≠ 0, since (a, 0) = a. Then by successive division we can write

so long as the remainders r₁, r₂, r₃, · · · are not 0. From an inspection of the inequalities at the right, we see that the successive remainders form a steadily decreasing sequence of positive numbers:

Hence after at most b steps (often many fewer, since the difference between two successive r’s is usually greater than 1) the remainder 0 must appear:

r_n–2 = r_n – 1q_n + r_n

r_n–1 = r_nq_n+1 + 0.

When this occurs we know that

(a, b) = r_n;

in other words, (a, b) is the last positive remainder in the sequence (5). This follows from successive application of the equality (3) to the equations (4), since from successive lines of (4) we have

(a, b) = (b, r₁), (b, r₁) = (r₁, r₂), (r₁, r₂) = (r₂, r₃),

(r₂, r₃) = (r₃, r₄),..., (r_n–1, r_n) = (r_n, 0) = r_n.

Exercise: Carry out the Euclidean algorithm for finding the greatest common divisor of (a) 187, 77. (b) 105, 385. (c) 245, 193.

An extremely important property of (a, b) can be derived from equations (4). If d= (a, b), then positive or negative integers k and 1 can be found such that

To show this, let us consider the sequence (5) of successive remainders. From the first equation in (4)

r₁ = a – q₁b,

so that r₁ can be written in the form k₁a + l₁b (in this case k₁ = 1, l₁ = – q₁). From the next equation,

Clearly this process can be repeated through the successive remainders r₃, r₄, ··· until we arrive at a representation

r_n = ka + lb,

as was to be proved.

As an example, consider the Euclidean algorithm for finding (61, 24); the greatest common divisor is 1 and the desired representation for 1 can be computed from the equations

61 = 2·24 + 13, 24 = 1·13 + 11, 13 = 1·11 + 2, 11 = 5·2 + 1, 2 = 2·1 + 0.

We have from the first of these equations

13 = 61 – 2·24,

from the second,

11 = 24 – 13 = 24 – (61 – 2·24) = –61 + 3·24,

from the third,

2 = 13 – 11 = (61 – 2·24) – (–61 + 3·24) = 2·61 – 5·24,

and from the fourth,

1 = 11 – 5·2 = (–61 + 3·24) – 5(2·61 – 5·24) = –11·61 + 28·24.

2. Application to the Fundamental Theorem of Arithmetic

The fact that d = (a, b) can always be written in the form d = ka + lb may be used to give a proof of the fundamental theorem of arithmetic that is independent of the proof given on page 23. First we shall prove, as a lemma, the corollary of page 24, and then from this lemma we shall deduce the fundamental theorem, thus reversing the previous order of proof.

Lemma: If a prime p divides a product ab, then p must divide a or b.

If a prime p does not divide the integer a, then (a, p) = 1, since the only divisors of p are p and 1. Hence we can find integers k and l such that

1 = ka + lp.

Multiplying both sides of this equation by b we obtain

b = kab + lpb.

Now if p divides ab we can write

ab = pr,

so that

b = kpr + lpb = p(kr + lb).

from which it is evident that p divides b. Thus we have shown that if p divides ab but does not divide a then it must divide b, so that in any event p must divide a or b if it divides ab.

The extension to products of more than two integers is immediate. For example, if p divides abc, then by twice applying the lemma we can show that p must divide at least one of the integers a, b, and c. For if p divides neither a, b, nor c, then it cannot divide ab and hence cannot divide(ab)c = abc.

Exercise: The extension of this argument to products of any number n of integers requires the explicit or implicit use of the principle of mathematical induction. Supply the details of this argument.

From this result the fundamental theorem of arithmetic follows at once. Let us suppose given any two decompositions of a positive integer N into-primes:

N = p₁p₂ · · · p_r = q₁q₂ · · · q₈.

Since p₁ divides the left side of this equation, it must also divide the right, and hence, by the previous exercise, must divide one of the factors qk. But q_k is a prime, therefore p₁ must be equal to this q_h. After these equal factors have been cancelled from the equation, it follows that p₂ must divide one of the remaining factors q_t, and hence must be equal to it. Striking out p₂ and q_t, we proceed similarly with p₃, ···, p_r. At the end of this process all the p’s will be cancelled, leaving only 1 on the left side. No q can remain on the right side, since all the q’s are larger than one. Hence the p’s and q’s will be paired off into equal couples, which proves that, except perhaps for the order of the factors, the two decompositions were identical.

3. Euler’s φ Function. Fermat’s Theorem Again

Two integers a and b are said to be relatively prime if their greatest common divisor is 1:

(a, b) = 1.

For example, 24 and 35 are relatively prime, while 12 and 18 are not. If a and b are relatively prime, then for suitably chosen positive or negative integers k and 1 we can write

ka + lb = 1.

This follows from the property of (a, b) stated on page 45.

Exercise: Prove the theorem: If an integer r divides a product ab and is relatively prime to a, then r must divide b. (Hint: if r is relatively prime to a then we can find integers k and l such that

kr + la = 1.

Multiply both sides of this equation by b) This theorem includes the lemma of page 46 as a special case, since a prime p is relatively prime to an integer a if and only if p does not divide a.

For any positive integer n, let φ(n) denote the number of integers from 1 to n which are relatively prime to n. This function φ(n), first introduced by Euler, is a “number-theoretical function” of great importance. The values of φ(n) for the first few values of n are easily computed:

We observe that φ(p) = p – 1 if p is a prime; for a prime p has no divisors other than itself and 1, and hence it is relatively prime to all of the integers 1, 2, 3, · · ·, p – 1. If n is composite, with prime decomposition

where the p’s represent distinct primes, each raised to a certain power, then

For example, since 12 = 2²·3,

as it should be. The proof is quite elementary, but will be omitted here.

* Exercise: Using Euler’s φ function, generalize Fermat’s theorem of page 37. The general theorem states: If n is any integer, and a is relatively prime to n, then

a^φ(n) = 1 (mod n).

4. Continued Fractions. Diophantine Equations

The Euclidean algorithm for finding the greatest common divisor of two integers leads immediately to an important method for representing the quotient of two integers as a composite fraction.

Applied to the numbers 840 and 611, for example, the Euclidean algorithm yields the series of equations,

840 = 1·611 + 229, 611 = 2·229 + 153,

229 = 1·153 + 76, 153 = 2·76 + 1,

which show, incidentally, that (840, 611) = 1. From these equations we may derive the following expressions:

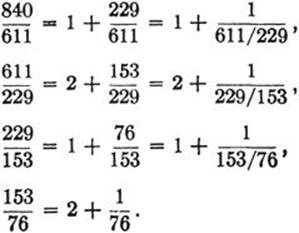
On combining these equations we obtain the development of the rational number in the form

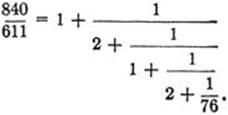
An expression of the form

where the a’s are positive integers, is called a continued fraction. The Euclidean algorithm gives us a method for expressing any rational number in this form.

Exercise: Find the continued fraction developments of

* Continued fractions are of great importance in the branch of higher arithmetic known as Diophantine analysis. A Diophantine equation is an algebraic equation in one or more unknowns with integer coefficients, for which integer solutions are sought. Such an equation may have no solutions, a finite number, or an infinite number of solutions. The simplest case is the linear Diophantine equation in two unknowns,

where a, b, and c are given integers, and integer solutions x, y are desired. The complete solution of an equation of this form may be found by the Euclidean algorithm.

To begin with, let us find d = (a, b) by the Euclidean algorithm; then for proper choice of the integers k and l,

Hence the equation (8) has the particular solution x = k, y = l for the case c = d. More generally, if c is any multiple of d:

c = d·q,

then from (9) we obtain

a(kq) + b(lq) = dq = c,

so that (8) has the particular solution x = x* = kq, y = y* = lq. Conversely, if (8) has any solution x, y for a given c, then c must be a multiple of d = (a, b); for d divides both a and b, and hence must divide c. We have therefore proved that the equation (8) has a solution if and only if c is a multiple of (a, b).

To determine the other solutions of (8) we observe that if x = x′, y = y′ is any solution other than the one, x = x*, y = y*, found above by the Euclidean algorithm, then x = x′ – x*, y = y′ – y* is a solution of the “homogeneous” equation

For if

ax′ + by′ = c and ax* + by* = c,

then on subtracting the second equation from the first we find that

a(x′ – x*) + b(y′ – y*) = 0.

Now the most general solution of the equation (10) is x = rb/(a, b), y = –ra/(a, b), where r is any integer. (We leave the proof as an exercise. Hint: Divide by (a, b) and use the Exercise on page 48.) It follows immediately that

x = x* + rb/(a, b), y = y* – ra/(a, b).

To summarize: The linear Diophantine equation ax + by = c, where a, b, and c are integers, has a solution in integers if and only if c is a multiple of (a, b). In the latter case, a particular solution x = x*, y = y* may be found by the Euclidean algorithm, and the most general solution is of the form

x = x* + rb/(a, b), y = y* – ra/(a, b),

where r is any integer.

Examples: The equation 3x + 6y = 22 has no integral solution, since (3, 6) = 3, which does not divide 22.

The equation 7x + 11y = 13 has the particular solution x = –39, y = 26, found as follows:

11 = 1.7 + 4, 7 = 1.4 + 3, 4 = 1.3 + 1, (7, 11) = 1.

1 = 4 – 3 = 4 – (7 – 4) = 2.4 – 7 = 2(11 – 7) – 7 = 2.11 – 3.7.

Hence

7.(–3) + 11(2) = 1,

7.(–39) + 11(26) = 13.

The other solutions are given by

x = –39 + 11r, y = 26 – 7r,

where r is any integer.

Exercise: Solve the Diophantine equations (a) 3x – 4y = 29. (b) 11x + 12y = 58. (c) 153x – 34y = 51.