High School Geometry Unlocked (2016)

GOALS

By the end of this chapter, you will be able to:

•Solve for area, circumference, radius, and diameter of a circle

•Find the incenter and circumcenter of a polygon

•Find the area or radius of a circle inscribed in a polygon, and vice versa

•Know the five types of regular polyhedra

•Understand cross-sections of prisms, spheres, cylinders, pyramids, and cones

•Know how to find volume and surface area of prisms, spheres, cylinders, pyramids, and cones

Lesson 5.1. From 2D to 3D

CIRCLES

In this lesson, we’ll review important facts and formulas regarding circles. A circle is defined as the set of points located at a fixed distance from a given central point.

A point is “on” a circle if it is on the edge of the circle, not inside or outside of it. A circle has an infinite number of points.

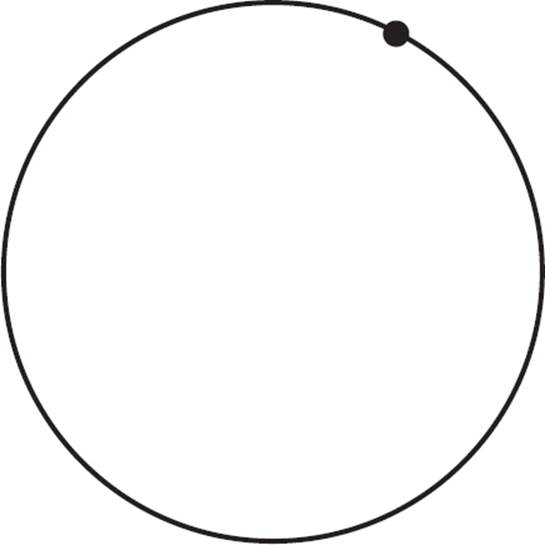
The radius is the distance from the center to the edge of the circle. The term radius can also refer to a line segment that is drawn as such.

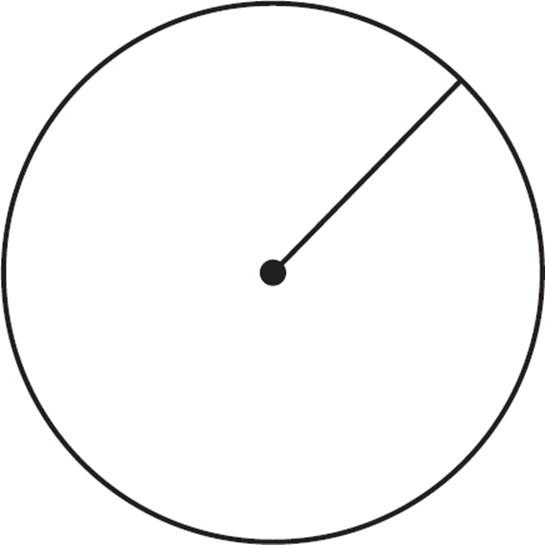
The diameter of a circle is the distance from edge to edge and through the circle’s center. The term diameter can also refer to a line segment that is drawn as such. The diameter is twice as long as the radius.

The circumference of a circle is the distance around the circle’s edge. A circle’s circumference is analogous to the perimeter of a polygon. The following formula gives the circumference of a circle:

Circumference of a Circle

Where r is the radius, and d is the diameter of a circle:

C = 2πr or C = πd

The value of π (a mathematical constant also known as pi) is actually defined by this relationship—the ratio of a circle’s circumference to its diameter.

The area of a circle is given by the following formula:

The value of π is
approximately equal
to 3.14. It’s an
irrational number,
which means that
it continues forever
without repeating.

Area of a Circle

Where r is the radius of a circle:

A = πr²

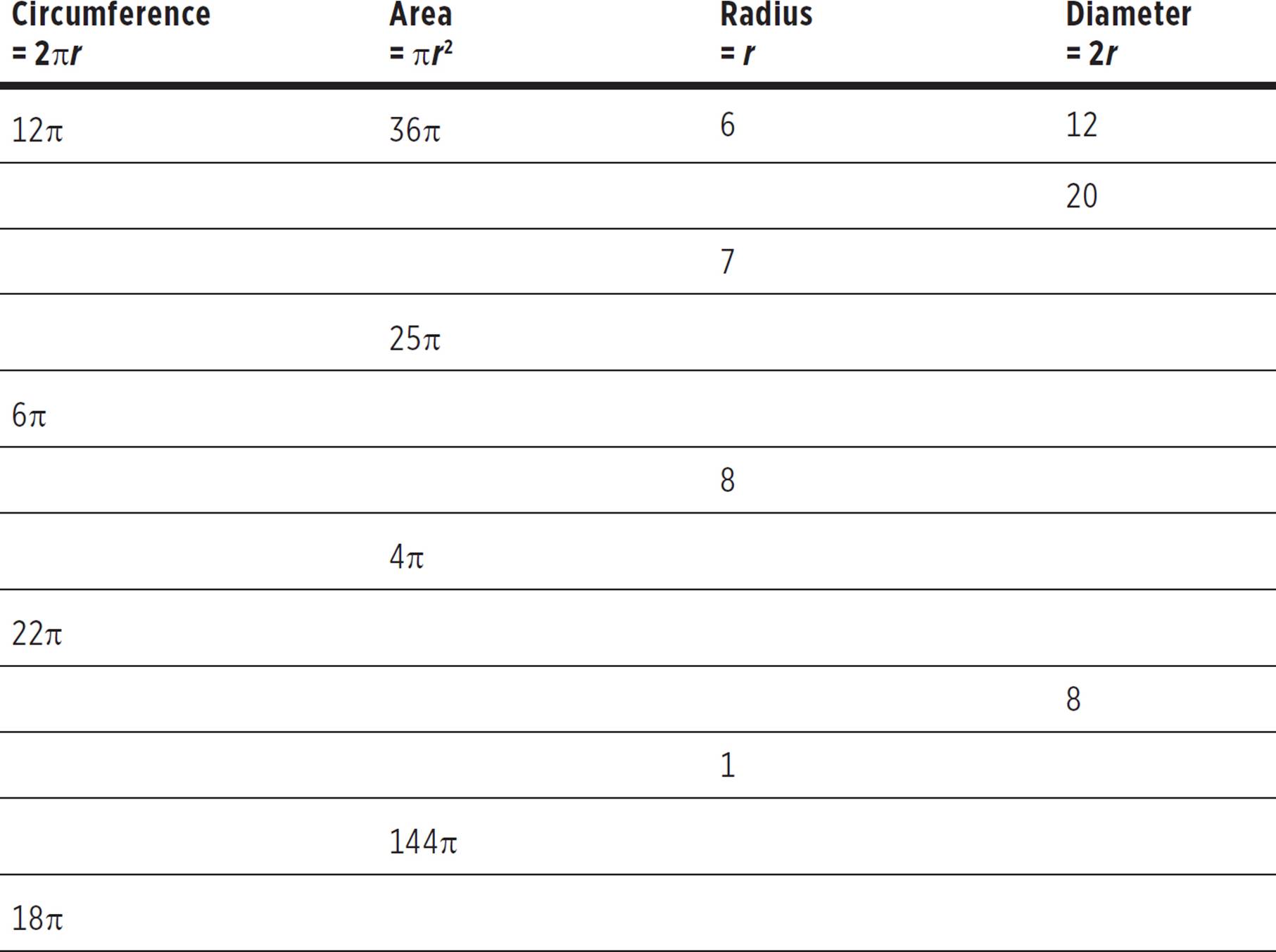
CARD

CARD is a mnemonic to remind you that all four of these elements of a circle—Circumference, Area, Radius, and Diameter—are related to one another. If you have just one of these values, you can easily solve for the other three.

Usually, it makes the most sense to solve for radius first; then plug radius into another formula to evaluate. The table below shows how to use the conventional equations to solve for radius.

CARD Exercise

Try completing the table on the following page. For example, if area is given in a row, try solving for radius first; then solve for circumference and diameter. The first row has been completed. Answers are at the end of the chapter.

Here is how you may see circles on the ACT.

The circumference of a circle is 50 inches. How many inches long is its radius?

F.

G.

H.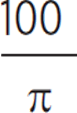

J.50π

K.100π

INCIRCLE AND CIRCUMCIRCLE

Incircle

The incircle of a polygon is a circle that is drawn inside the polygon and is tangent to every side. Another term for incircle is inscribed circle. The center of an incircle is called the incenter.

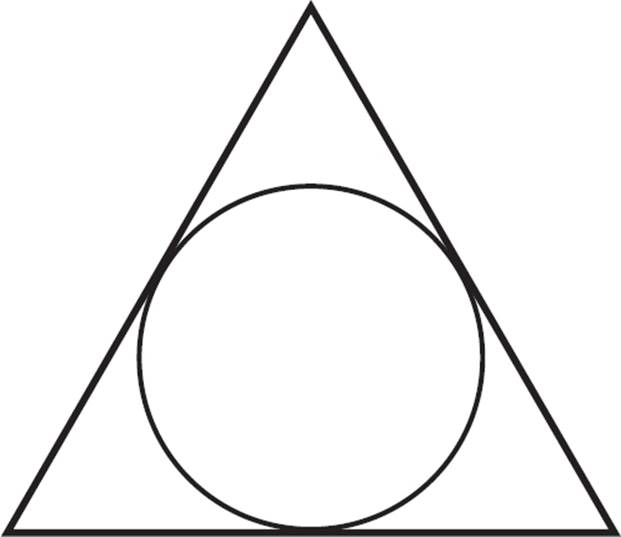
All triangles have incircles, as do all regular polygons. Irregular polygons with more than three sides will not necessarily have have an incircle that touches every side.

Some sources use a looser definition of “incircle,” which can apply to all irregular polygons: “An incircle is the largest circle that can be drawn completely inside a given polygon.”

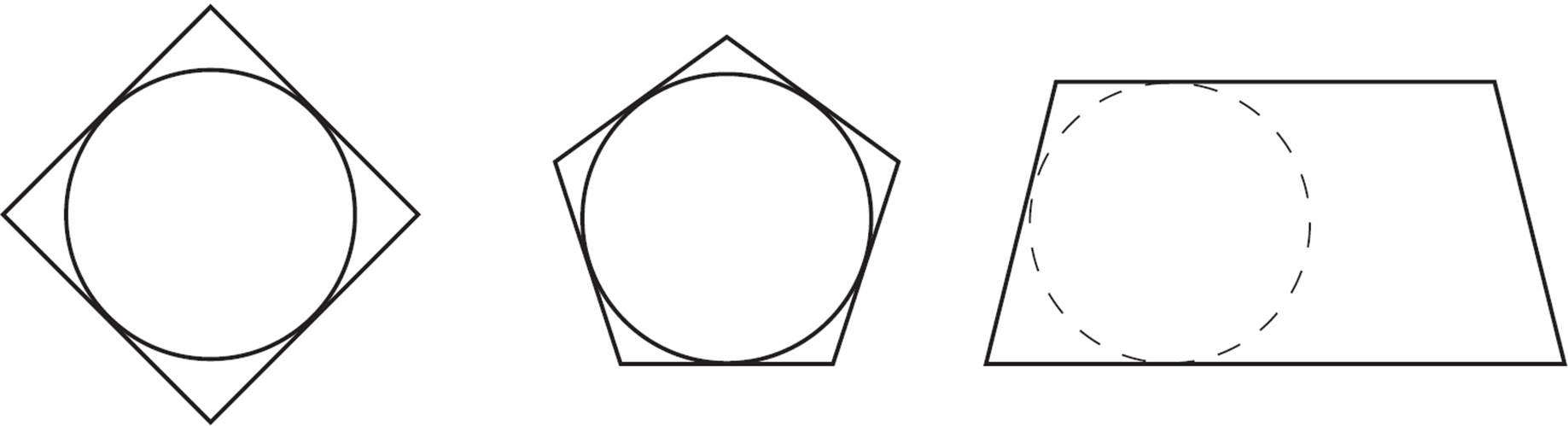
Some of these polygons have an incircle, while others do not.

The radius of the incircle is known as the apothem or inradius. An apothem segment connects the incenter to a given side of the polygon, and is also perpendicular to that side. If a polygon has an incircle, then each side of the polygon has one apothem.

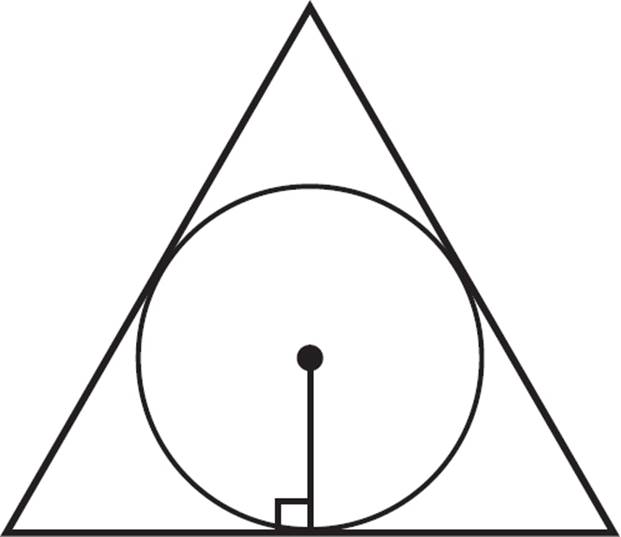
Circumcircle

The circumcircle of a polygon is a circle that is drawn outside the polygon and touches every vertex. Another term for circumcircle is circumscribed circle. The center of a circumcircle is called the circumcenter.

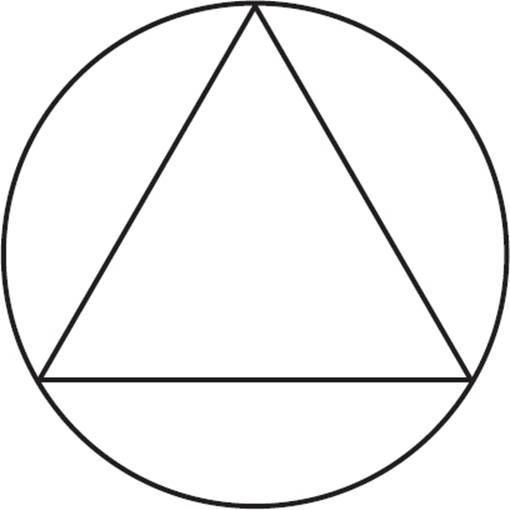
All triangles have circumcircles, as do all regular polygons. Irregular polygons with more than three sides will not necessarily have a circumcircle that touches every side.

The formula for the circumference of a circle is C = 2πr. So, 50 = 2πr and, therefore, r = 25/π. Choice (G) is the result of forgetting to divide by the 2 in the formula. Choice (H) could result by mistakenly multiplying 50 by 2 rather than dividing when using the formula. Choices (J) and (K) incorrectly solve for the radius. The correct answer is (F).

Some sources use a looser definition of “circumcircle,” which can apply to all irregular polygons: “A circumcircle is the smallest circle that can be drawn completely outside a given polygon.”

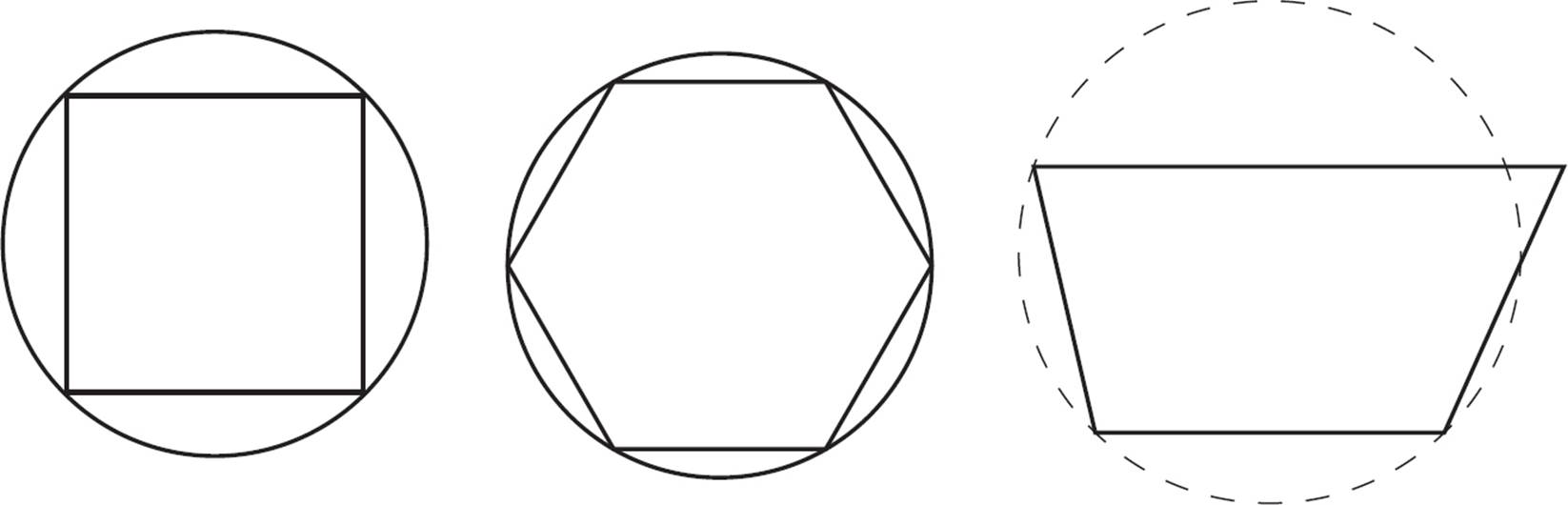
Some of these polygons have a circumcircle, while others do not.

The radius of the circumcircle is known as the circumradius or just radius. A circumradius segment connects the circumcenter to a given vertex of the polygon. If a polygon has a circumcircle, then each vertex of the polygon has a circumradius.

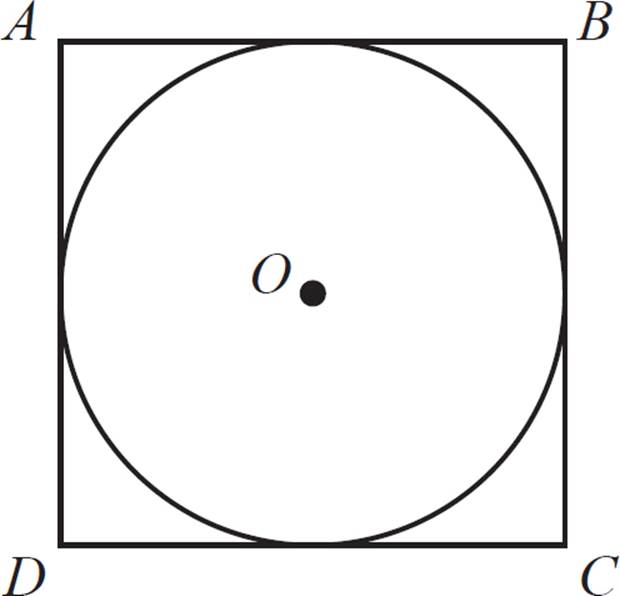
Which of the following statements is true? (Check all that apply.)

□ The circle is inscribed in the square.

□ The square is inscribed in the circle.

□ The circle is circumscribed around the square.

□ The square is circumscribed around the circle.

To answer this question, make the assumption that the circle is tangent to each side of the square. Incidentally, if that weren’t true, then none of the above statements would be correct.

For this figure, the first and fourth statements are correct. The circle is inscribed in the square, and the square is circumscribed around the circle. Both statements mean the same thing.

WORKING WITH INSCRIBED FIGURES

Some geometry exercises will have you find the area (or other values) of inscribed or circumscribed figures. In general, when solving these problems, you should focus on places that the two figures intersect. In this lesson, we’ll focus on a few examples of circles that are inscribed or circumscribed with polygons.

Circles and Squares

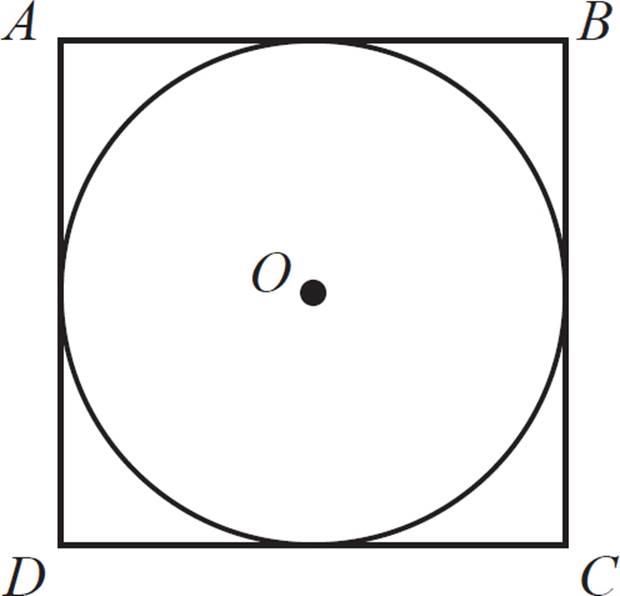
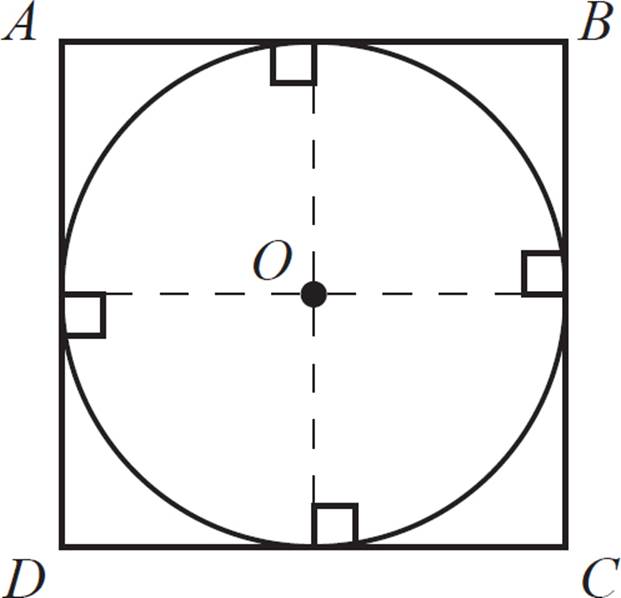
In the figure above, the circle with center O has a radius of 5 and is inscribed in square ABCD. Find the area of square ABCD.

Supplies

Access your student
tools to download
larger, printable
versions of the images
in this section.

First, draw the circle’s radii at the points of intersection (the midpoints of the square’s sides). By the definition of an inscribed circle, you know that the sides of the square are tangent to the circle, and each tangent line is perpendicular to the radius drawn at the point of tangency.

It’s important to
draw the radii at the
points where the two
figures intersect. If you
draw radii anywhere
else, it won’t tell you
much, because you’d
have to figure out
how to account for
the gap between the
circle and square.

Since ABCD is defined as a square, it’s easy to see that the opposite midpoints of the square (also the tangent points for the circle) form diameters of the circle. That means that the diameter of the circle is congruent to the side of the square. (Recall that the radius of the circle was given as 5.)

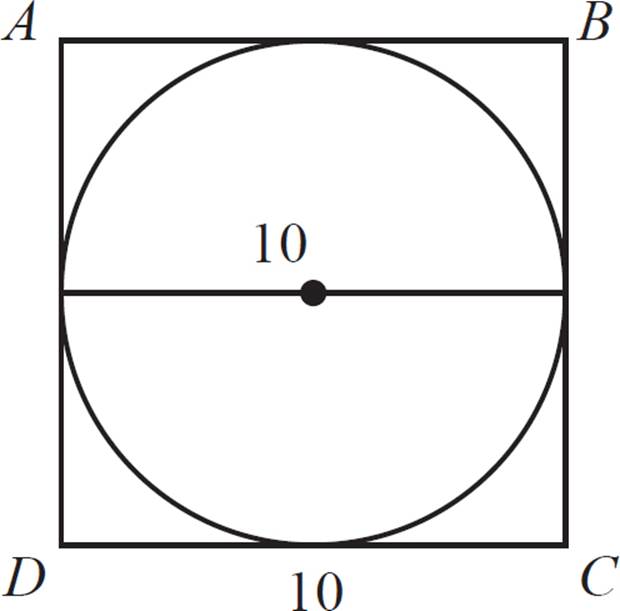
Therefore, the length of the side of the square is known. The area of a square is side × side, or side². For the area of this square, just multiply 10 × 10 = 100.

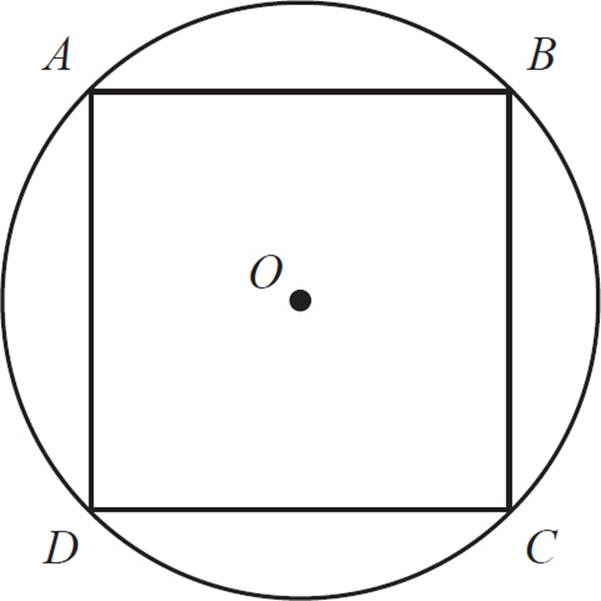
In the figure above, square ABCD has an area of 64 and is inscribed in the circle with center O. Find the area of circle O.

First, draw the circle’s radii at the points of intersection (the square’s vertices). This is a little different from the previous example, since the diameter of the circle is congruent to the square’s diagonals, not its sides. You’ll just have to do a couple more steps to solve for the length of the diagonal.

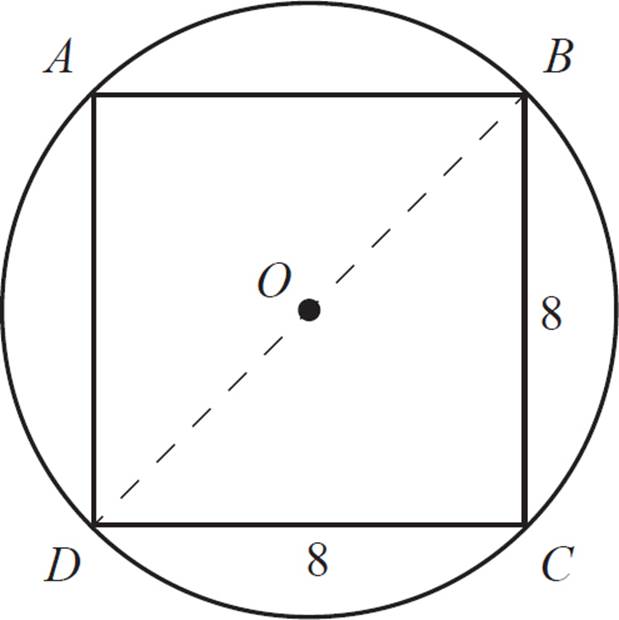
The square has a given area of 64. To solve for the side of the square, just calculate = 8. Then, use the Pythagorean theorem to solve for the diagonal:

a² + b² = c²

8² + 8² = c²

64 + 64 = c²

128 = c²

= c

× = c

8 = c

You may also recall the ratio for the sides of a 45°−45°−90° triangle. (This is also the triangle formed from the diagonal of a square).

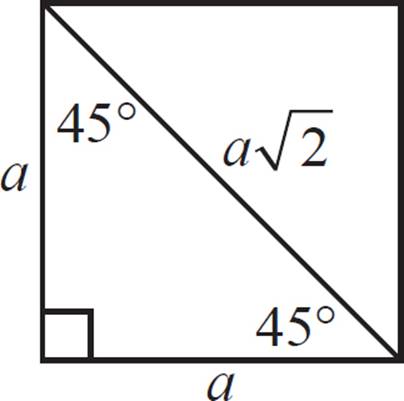
Therefore, the diagonal of this square is 8, which is also congruent to the diameter of the circle. The radius of the circle would be equal to half of that, which is 4. Now that you have the radius, you can solve for the area of the circle:

A = π r²

A = π (4)²

A = π × 4² × ()²

A = π × 16 × ()²

A = π × 16 × 2

A = 32π

Circles and Equilateral Triangles

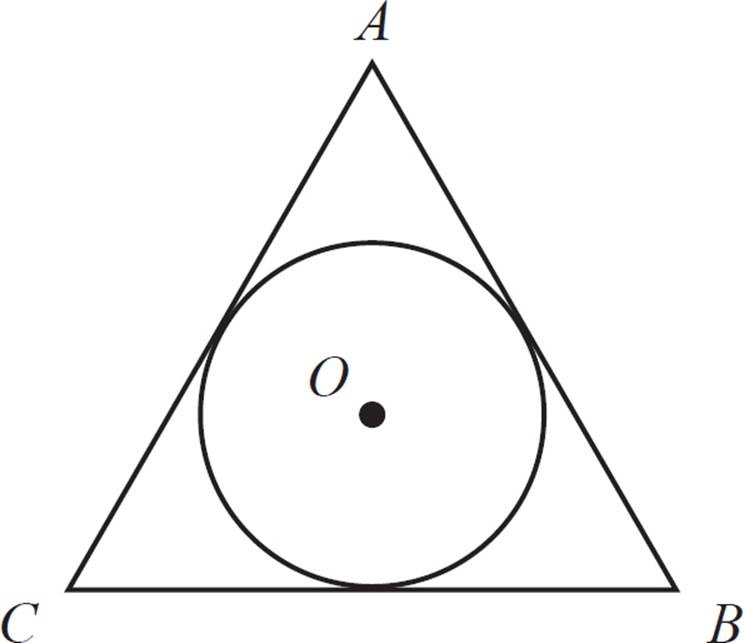
In the figure above, circle O has a radius of 2 and is inscribed in the equilateral triangle ABC. Find the area of triangle ABC.

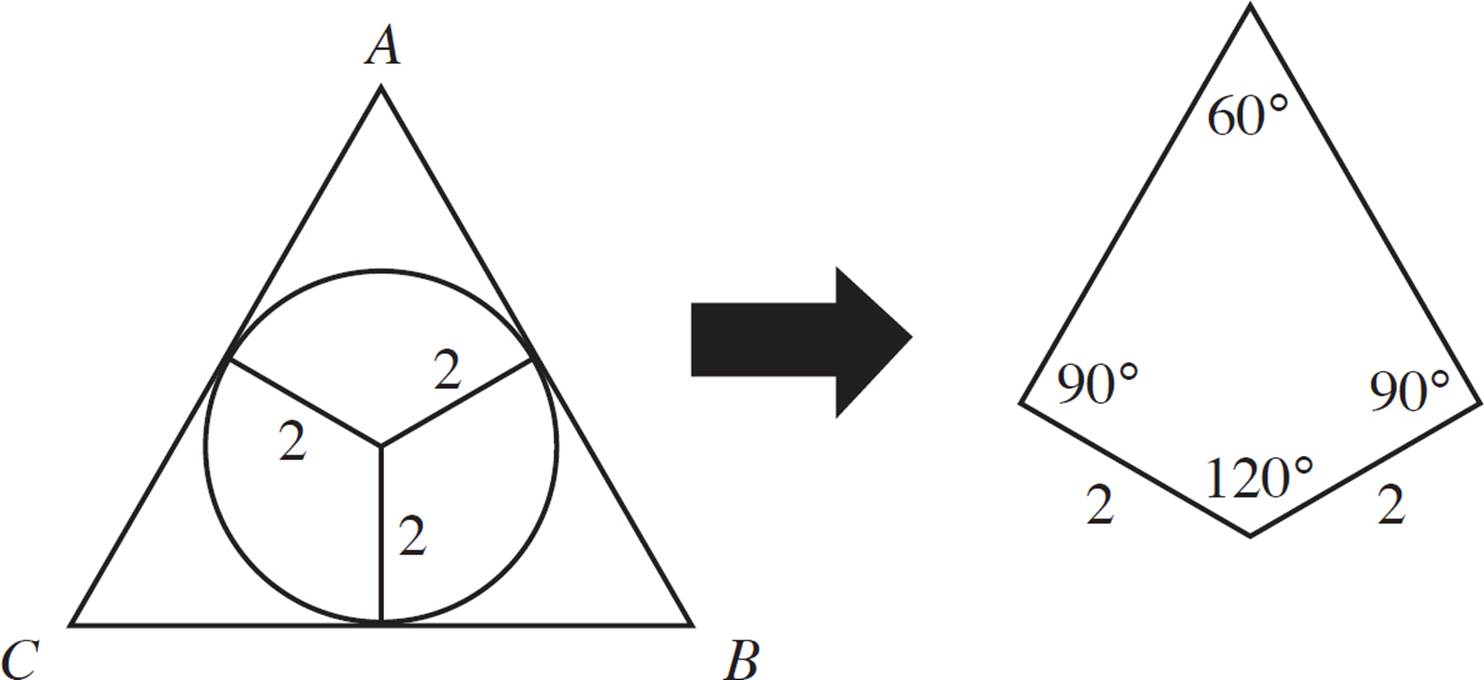
First, draw the circle’s radii at the points of intersection (the midpoints of the triangle’s sides). This forms three congruent quadrilaterals, with the angles 60°, 90°, 90°, and 120°. How do we know that? The 60° comes from the vertex angle of the triangle. Since the triangle is equilateral, we know that the vertex angles are each equal to 60°. The 90° angles are the ones formed at the tangent points. From the definition of tangent points, we know that the radii intersect at 90°. Finally, the 120° angle is what’s left when you subtract 360° − (60° + 90° + 90°).

Here is how you may see inscribed figures on the ACT.

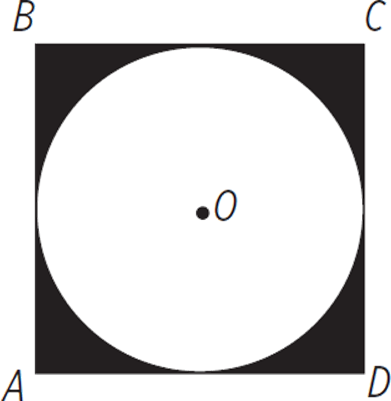
In the figure below, the circle with center O is inscribed inside square ABCD as shown. If a side of the square measures 8 units, what is the area of the shaded region?

F.8 − 16π

G.8π

H.16π

J.64 − 16π

K.64π

Recall that the
sum of angles in a
quadrilateral is 360°.

Next, if we divide these quadrilaterals in half, we get a special right triangle: the 30°−60°−90°. Recall that the ratio for the sides of such a triangle is x : x : 2x. We can use this to solve for the lengths of the sides of the small right triangle, which will give us information about triangle ABC.

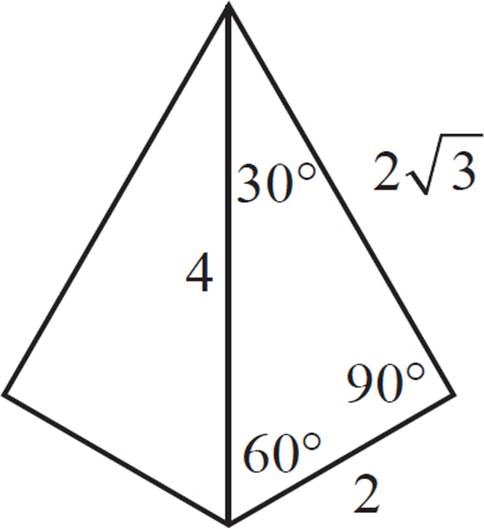
Perhaps the simplest way to find the area of triangle ABC is to find the area of this small right triangle, and multiply that by 6, since there are 6 such triangles that make up ABC. Find the area of the small right triangle.

A = bh

A = × 2 × 2

A = 1 × 2

A = 2

Now, multiply that by 6 to find the area of ABC: 6 × 2 = 12.

The area of triangle ABC is 12.

Note that we can also find the lengths of the sides, as well as the height, of triangle ABC.

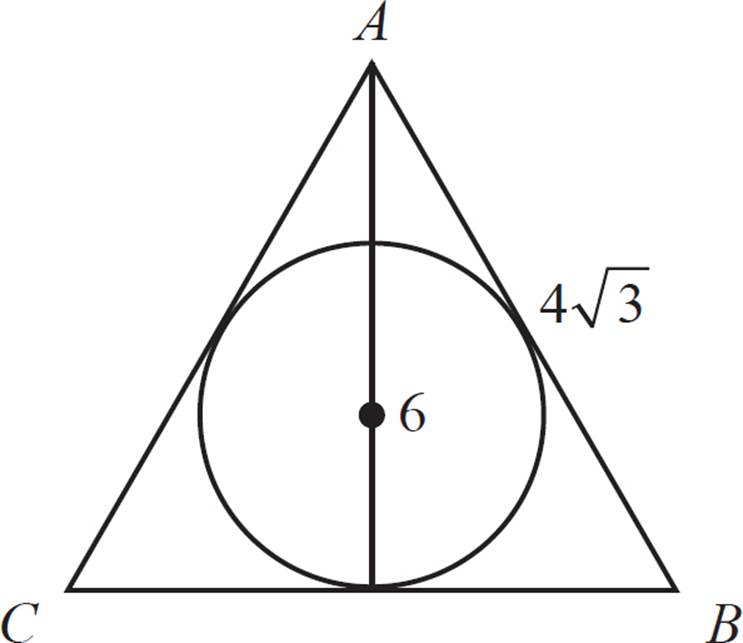
The length of each side is 4.

Using these lengths to calculate the area of ABC, we get the same value of 12.

A = bh

A = × 6 × 4

A = 3 × 4

A = 12

The area of triangle ABC is 12.

Mark the side of the square “8,” and write down the formulas for the area of a circle and square: πr² and s².

Is there a formula for the shape made by the shaded region? Nope. We just need the basic formulas for the basic shapes. 8² = 64, so we at least know the shaded region is less than 64, the area of the square. But what’s the link between the square and the circle? The side of the square equals the diameter. So if the diameter is 8, then the radius must be 4. Use that in the area formula: 4²π = 16π. Subtract the area of the circle from the area of the square, and we get (J), the correct answer.

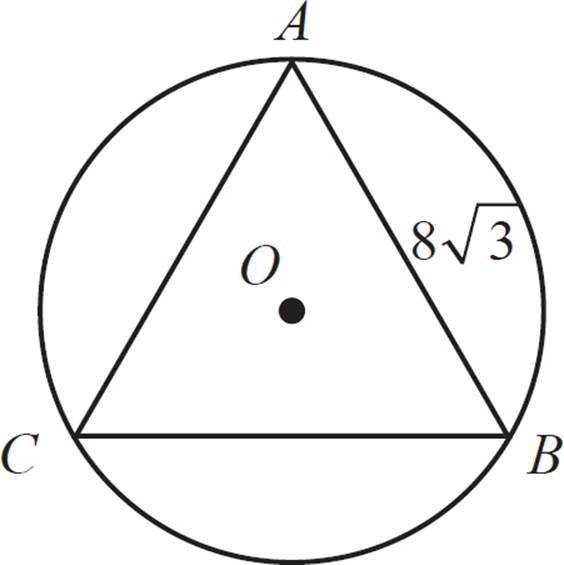
In the figure above, triangle ABC is equilateral with a side length of 8, and it is inscribed in the circle with center O. Find the area of circle O.

First, draw the circle’s radii at the points of intersection (the triangle’s vertices). This forms three congruent triangles, with the angles 30°, 30°, and 120°. How do we know that? One way to think of it is that a circle has 360°, which we’ve divided into three equal parts at the center. We know that they are equal parts, because it is an equilateral triangle that is inscribed in the circle. Therefore, each of the three angles formed at the center of the circle is equal to 120° (= 360°/3).

We also know that each of these triangles is isosceles, since two of the sides are congruent to the radius of the circle. Therefore, the two smaller angles must be congruent. We can solve for this angle measure using an equation:

180° − 120° = 2x

60° = 2x

30° = x

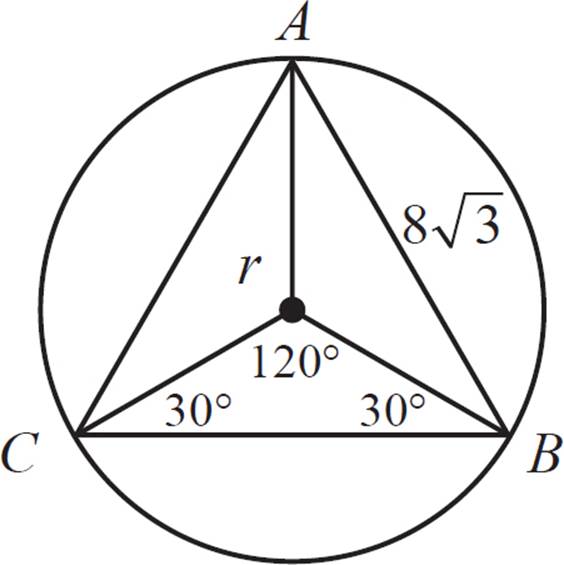
Next, if we divide these triangles in half, we get a special right triangle: the 30°−60°−90°. Recall that the ratio for the sides of such a triangle is x : x : 2x. We can use this to solve for the lengths of the sides of the small right triangle, which will give us information about circle O.

If the side length of triangle ABC is 8, then half of that is 4. For the small triangle, this is the length of the side opposite 60°.

From there, we can derive that the shortest side of the small triangle is 4, and the longest side is 8.

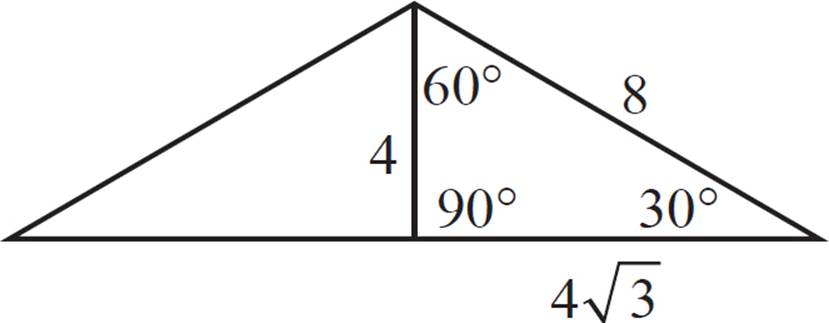
The long side of the small right triangle is congruent to the circle’s radius. Therefore, the radius of circle O is 8. Calculate the area of the circle:

A = π r²

A = π × 8²

A = π × 64

A = 64π

The area of circle O is 64π.

Note that we can also find the height, as well as the area, of triangle ABC.

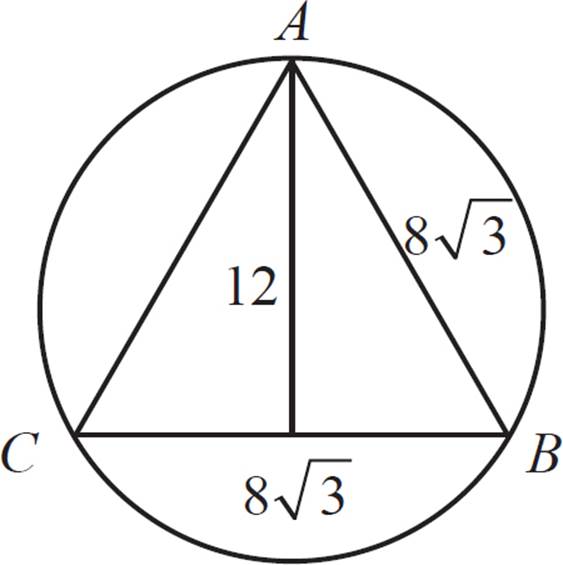
The height is 12. The area of ABC is ( × 12 × 8), or (6 × 8).