High School Geometry Unlocked (2016)

Lesson 5.3. Volume and Surface Area

Volume is the amount of 3-dimensional space that is occupied by a solid. You’ve probably noticed that beverages and other fluids are sold in containers marked for volume—quarts, gallons, and so on. You can also measure volume in “cubic” units, such as the cubic inch (a cube that is 1 inch on every side). In this chapter, you’ll learn volume formulas for some of the most common types of 3-dimensional solids. You can use these formulas on more complex figures too, by breaking up a shape into smaller, more recognizable pieces.

Surface area is the amount of 2-dimensional area that is taken up by the surface of a figure. For example, the surface area of a cube is the sum of the areas of each of its six faces. In this chapter, you’ll learn surface area formulas for some of the most common types of 3-dimensional solids. To calculate surface area on more complex figures, just remember that you need to calculate the area of every face on the figure.

PRISMS AND CYLINDERS

You can think of a prism as a two-dimensional shape that is stacked on top of itself to have a non-zero height. For example, a single sheet of sticky note paper can be thought of as a two-dimensional rectangle, but a whole pad of sticky notes would be a prism.

Volume

Some types of prisms have volume formulas that are fairly easy to remember. But whenever you don’t know a formula for a certain prism, here is a general rule that works for every one: To calculate the volume for a prism, first find the area of the base (one of the two congruent faces on opposite sides of the figure); then multiply by the height.

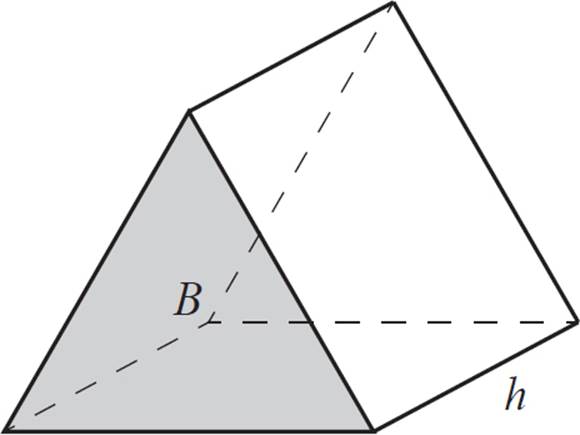
Volume of a Prism

The volume of any prism is equal to the area of the base, multiplied by the height of the prism.

Volume = B × h

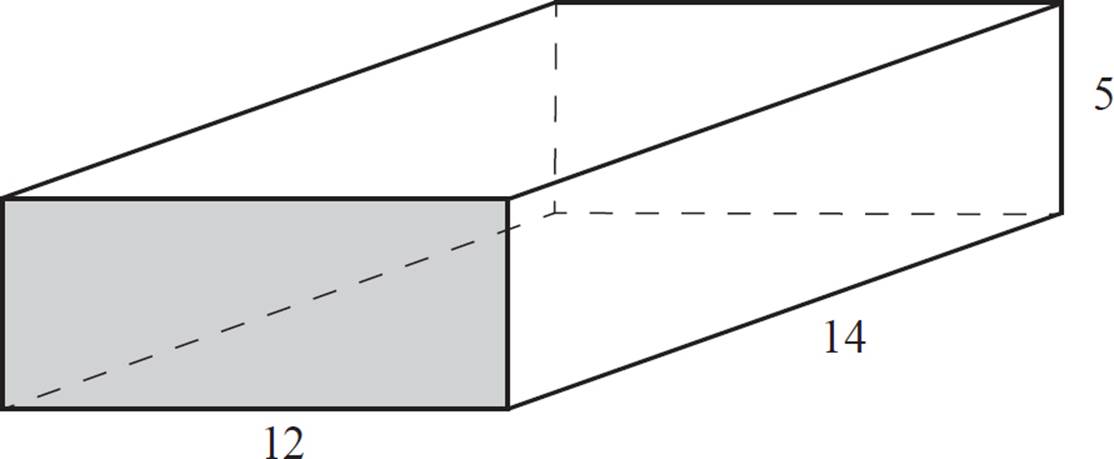
Find the volume of the rectangular prism shown above.

In the formula V = Bh,
we use the capital
letter for “B” to
remind you that you’re
finding the area of
the base, not just the
length or the width.

To calculate the volume of the prism, you’ll first need to calculate the area of the base. Note that in a rectangular prism, you can actually consider any of the faces as the “base,” since each pair of faces is parallel and congruent to each other.

Therefore, just pick any of the six faces and call it the base. For this example, we’ll use the front face. This is a rectangle with width 5 and length 12. Calculate the area:

A = 5 × 12

A = 60

Then, multiply that area by the height of the prism.

V = 60 × 14

V = 840

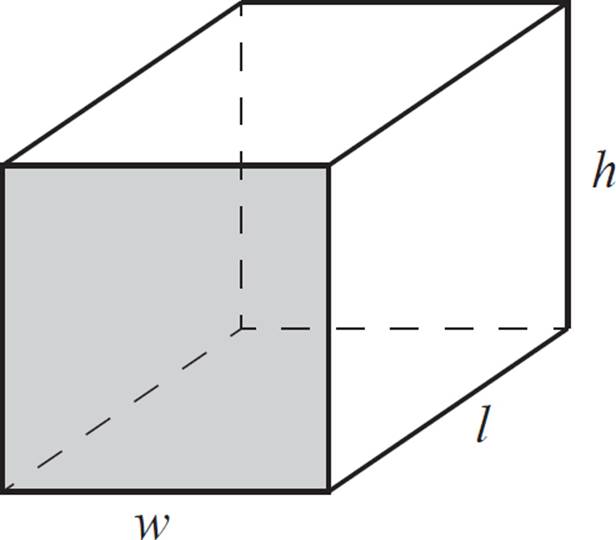
To calculate the volume of a rectangular prism, you can use this straightforward formula:

Volume of a Rectangular Prism

Where l is the length, w is the width, and h is the height of the prism:

Volume = l × w × h

Here is how you may see volume of a prism on the SAT.

If a rectangular swimming pool has a volume of 16,500 cubic feet, a uniform depth of 10 feet, and a length of 75 feet, what is the width of the pool, in feet?

A.22

B.26

C.32

D.110

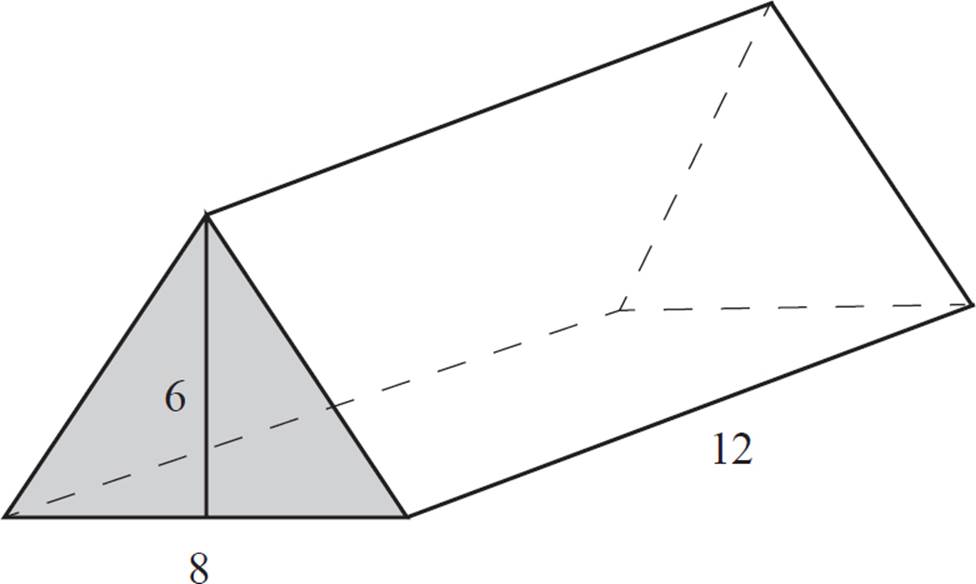
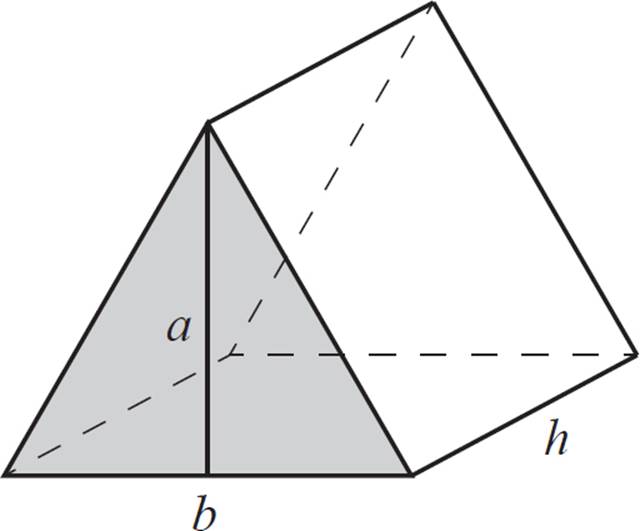
Find the volume of the triangular prism shown above.

To calculate the volume of the prism, you’ll first need to calculate the area of the triangular base. Note that the triangles are considered the “bases” of this prism because they are congruent and parallel to each other. The other, rectangular faces are not parallel to each other, so they are not the bases.

The area of a triangle is given as A = bh, and you know both the base and height of this triangle. Plug in the values and solve for A.

A = × 8 × 6

A = × 48

A = 24

Finally, multiply that area by the height of the prism.

V = 24 × 12

V = 288

From our calculations above, we can derive the following formula:

Volume of a Triangular Prism

Where b is the length of the triangular base, a is the altitude of the triangular base, and h is the height of the prism:

Volume = × a × b × h

For this question, you need to know that volume equals length × width × height. You know that the volume is 16,500, the depth (or height) is 10, and the length is 75. Just put those numbers into the formula: 16,500 = 75 × w × 10. Use your calculator to solve for w, which equals 22: The correct answer is (A).

Volume of a Cylinder

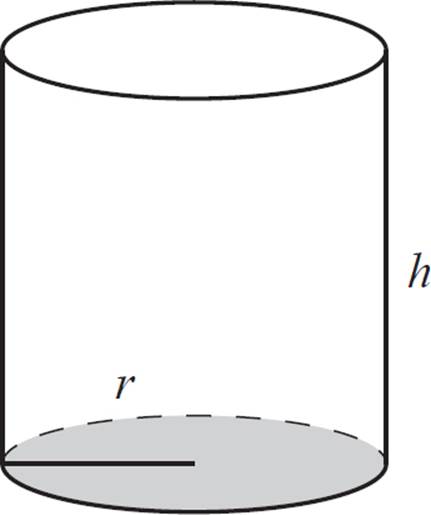
Find the volume of the cylinder shown above.

To calculate the volume of the cylinder, use the same basic idea as with a prism: Calculate the area of the base; then multiply by the height. First, calculate the area of the circular base.

The area of a circle is given as A = πr², and you know the radius for this circle.

A = πr²

A = π × 5²

A = 25π

Finally, multiply that area by the height of the cylinder.

V = 25π × 20

V = 500π

From our calculations above, we can derive the following formula:

Volume of a Cylinder

Where r is the radius of the circular base, and h is the height of the cylinder:

Volume = πr² × h

Here is how you may see volume of a cylinder tested on the SAT.

A cylindrical water tank has a diameter of 20 meters and a height of 20 meters. If the tank currently holds 1600 cubic meters of water, what is the approximate depth of the water in the tank?

A.5 m

B.10 m

C.15 m

D.20 m

Surface Area

As with volume, some types of prisms have formulas for surface area that are fairly straightforward. But whenever you don’t know a formula for a certain prism, the general rule is to add up the areas of every face.

Surface Area of a Prism

The surface area (SA) of any prism is the sum of the areas of all of its faces.

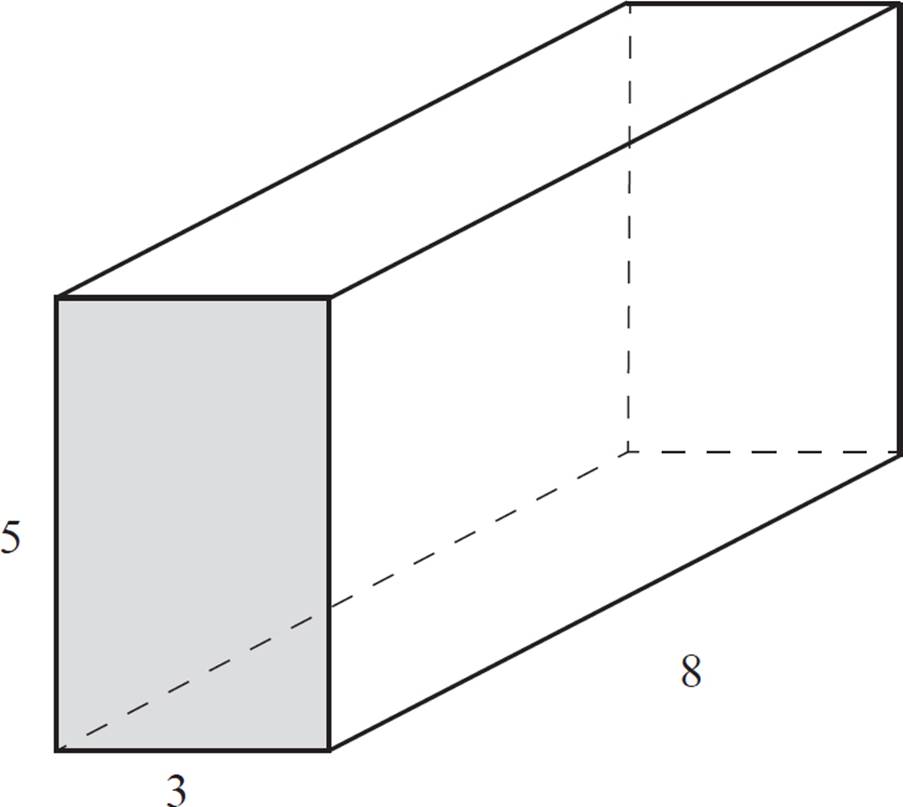
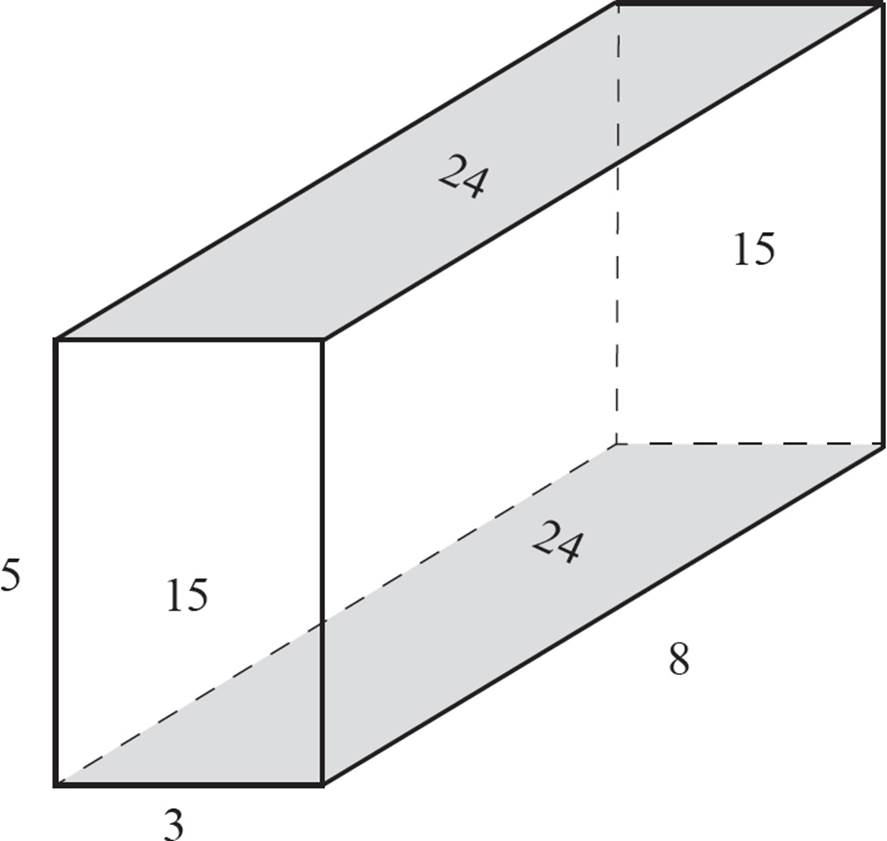
Find the surface area of the rectangular prism shown above.

To calculate the surface area of the prism, calculate the areas of its faces. Note that in a rectangular prism, each pair of opposite faces is congruent, so you’ll only need to calculate the areas of three faces (or less, in some cases). The same would be true for an oblique rectangular prism.

Start with any face, and calculate the area. For this example, we’ll start with the front face:

A = 3 × 5

A = 15

Therefore, the area of the front face is 15, so you also know that the area of the back face is 15, since opposite faces are congruent.

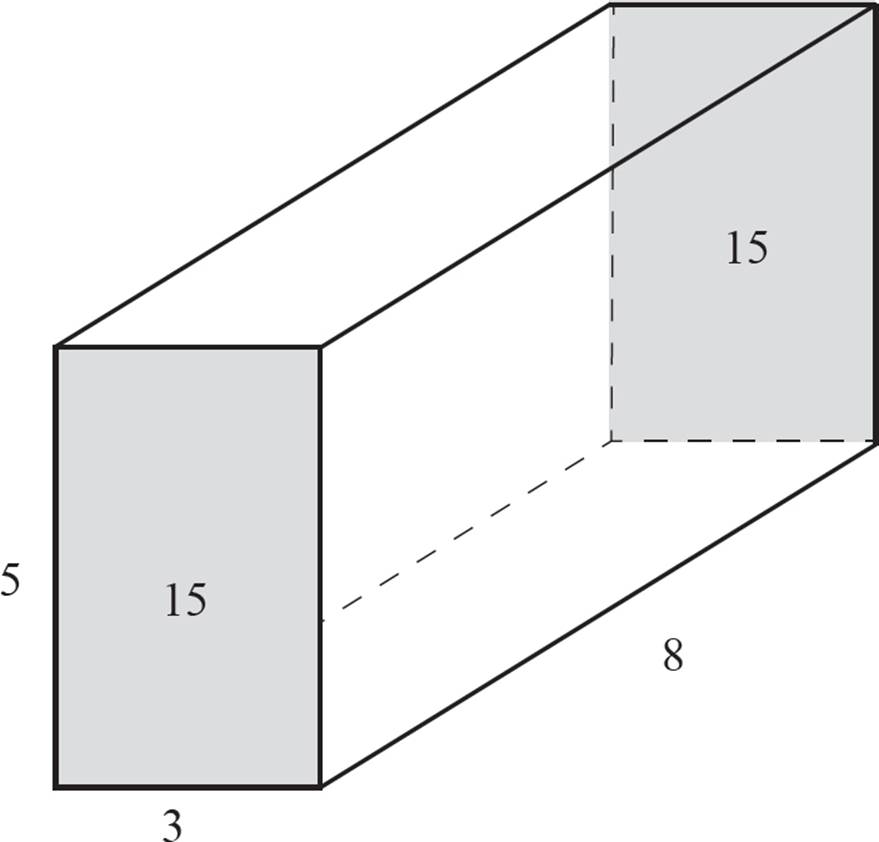
Find the area of a different face. We’ll go with the one that’s on the bottom:

A = 3 × 8

A = 24

Therefore, the bottom and top faces each have an area of 24.

The height of the water tank doesn’t matter in this problem. Use the formula for volume of a cylinder (V = πr² × h) and plug in the information you have. It should look like this: 1600 = (π)(10²)h. When you solve for h, you get a number very close to 5. Since the question asks for the approximate depth of the water, (A) is the best answer.

The last pair of faces to calculate is the two side faces. Calculate the area of one of these sides:

A = 5 × 8

A = 40

Therefore, the left and right faces each have an area of 40.

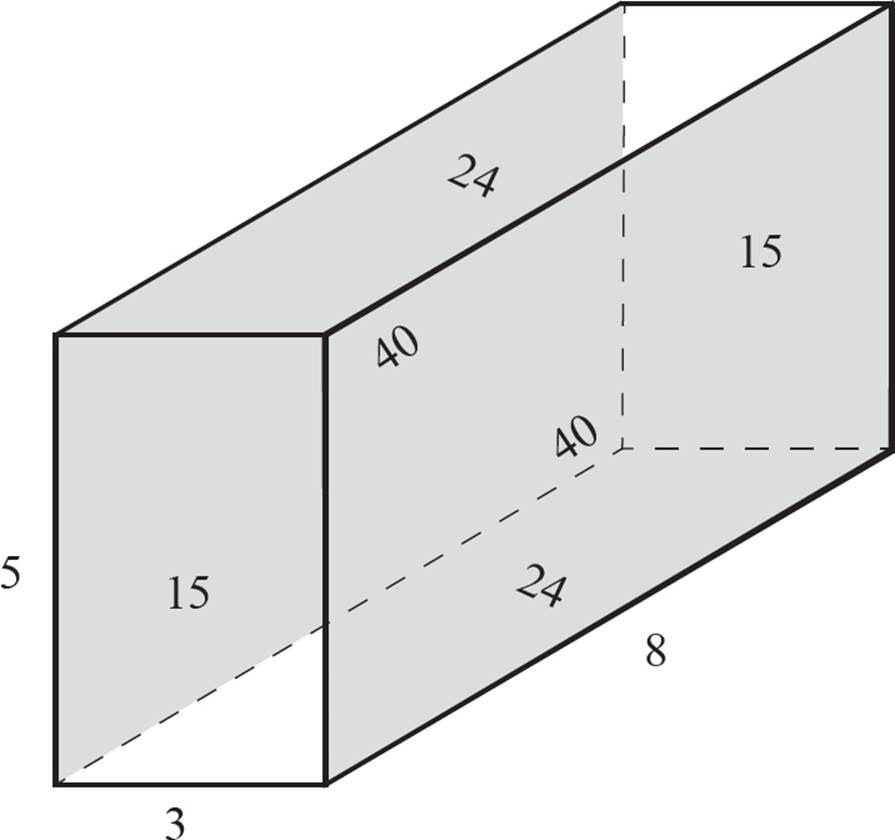
Finally, add all of these numbers together, making sure to include all six faces:

SA = 15 + 15 + 24 + 24 + 40 + 40

You can simplify first, if you like:

SA = 2 × 15 + 2 × 24 + 2 × 40

SA = 2 (15 + 24 + 40)

SA = 2 × (79)

SA = 158

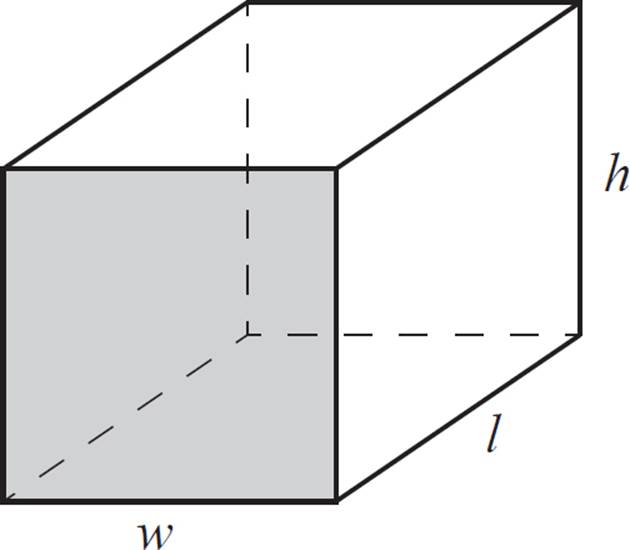
Surface Area of a Rectangular Prism

Where l is the length, w is the width, and h is the height of the prism:

Surface Area = 2(lw + lh + wh)

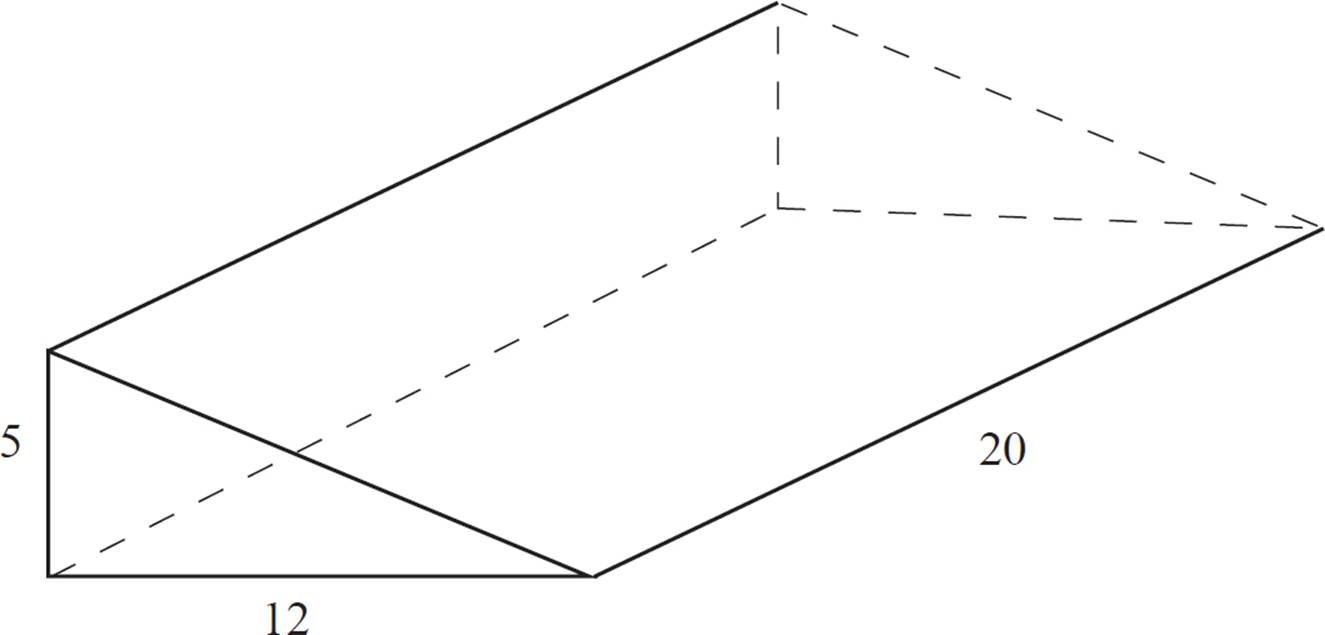
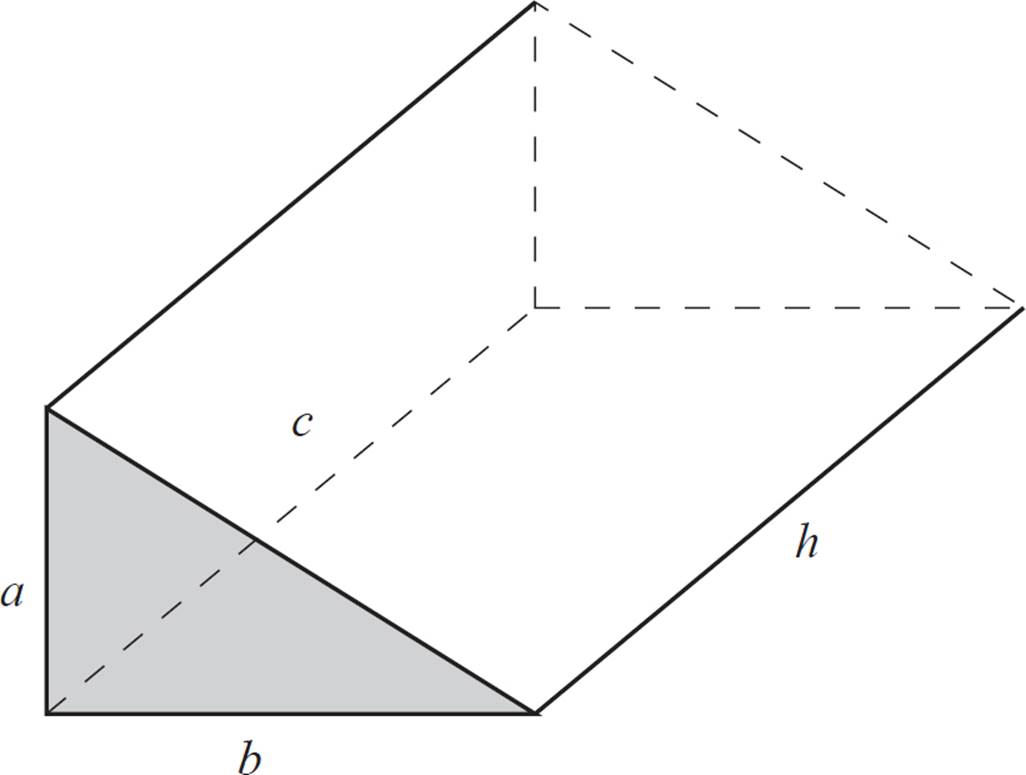
Find the surface area of the triangular prism shown above.

To calculate the surface area of the prism, we’ll need to calculate the areas of its faces. Note that in a triangular prism, the pair of triangular bases is congruent, but the three rectangular faces may not be congruent.

The area of a triangle is given as A = bh, but there are two of these triangles, so just simplify the pair to bh. Plug in the values and solve for area:

Therefore, the two triangular bases together have an area of 60.

Next, find the area of each rectangular face. Looking at the side face, the length and width are 5 and 20. Calculate the area:

A = 5 × 20

A = 100

The bottom face has length and width of 12 and 20. Calculate the area:

A = 12 × 20

A = 240

The slanted face has a length of 20, but the width (the slant of the triangle) is not labeled. You’ll have to calculate it, using the Pythagorean theorem.

a² + b² = c²

5² + 12² = c²

25 + 144 = c²

25 + 144 = c²

169 = c²

  = c

13 = c

Therefore, the width of the slanted side is 13. Calculate the area of the slanted triangular face:

A = 13 × 20

A = 260

Finally, add the areas of all the faces together:

SA = 60 + 100 + 240 + 260

SA = 660

Surface Area of a Prism with a Right Triangle Base

Where a and b are the legs of the triangle, c is the hypotenuse of the triangle, and h is the height of the prism:

Surface Area = ab + ah + bh + ch

Prism Exercise

Can you come up with a similar formula for a prism whose base is a non-right triangle? Assume that the sides and altitude of the triangle are given, as well as the height of the prism.

Answers are at the end of the chapter.

Surface Area of a Cylinder

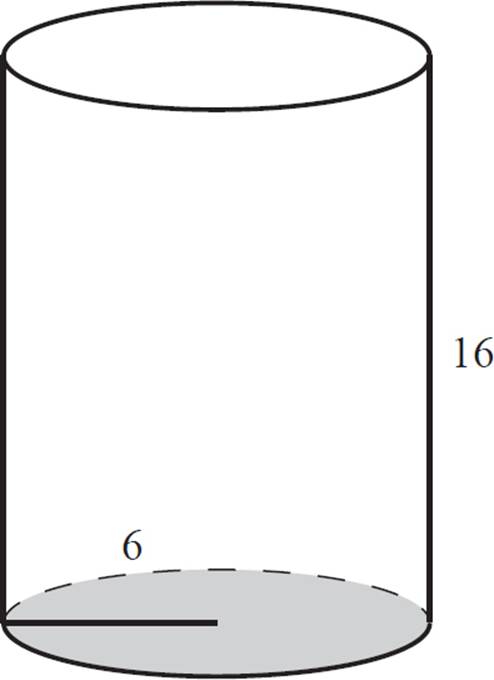
Find the surface area of the cylinder shown above.

To calculate the surface area of the cylinder, calculate the areas of its faces. But these faces are round! Here’s how to do it.

Start with the circular bases, and calculate the area. Go ahead and multiply πr² × 2, since there are two congruent circular faces.

Therefore, the area of the two circular bases together is 72π.

Now, calculate the area of the curved face. The height is given as 16, but what about the length? Imagine having a cardboard tube that you slice open. If you flatten out the tube, the length of the previously curved edge is equal to the circumference of the circle.

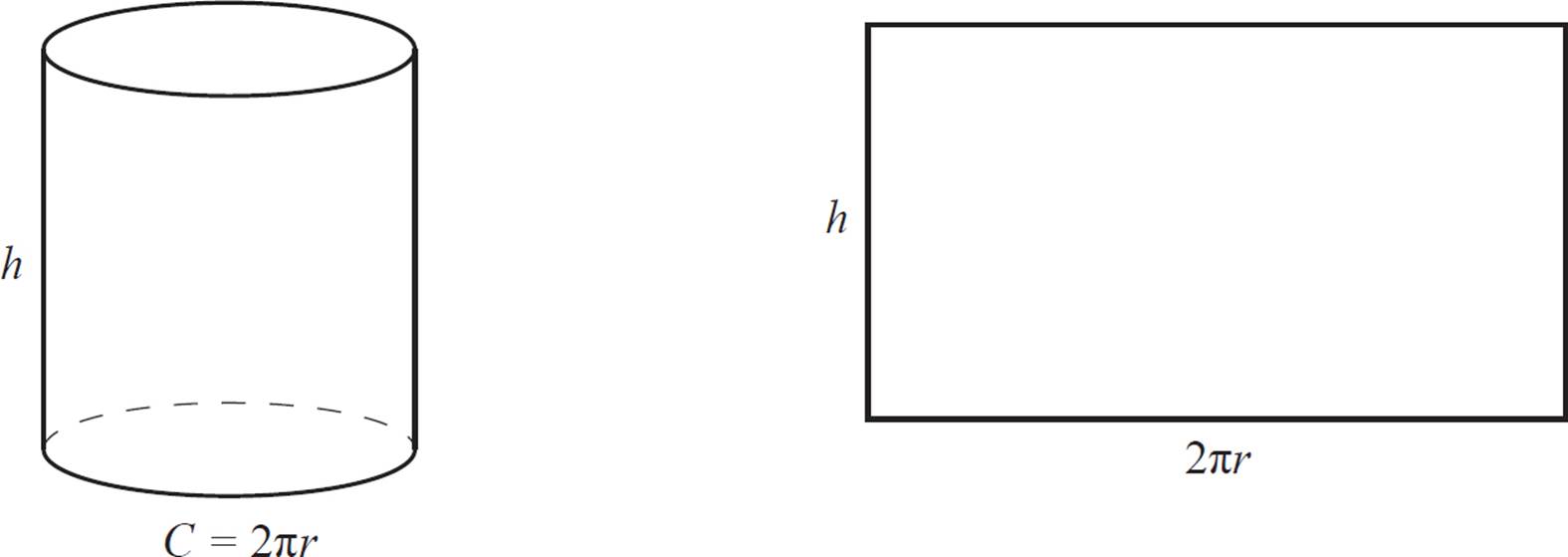
The circumference of a circle is given as 2πr. Calculate the circumference of our circle:

C = 2πr

C = 2π × 6

C = 12π

To calculate the area of the curved “face,” multiply the circumference by the height of the cylinder.

A = 12π × 16

A = 192π

Finally, add the areas together:

SA = 192π + 72π

SA = 264π

From our calculations above, we can derive the following formula:

Surface Area of a Cylinder

Where r is the radius and h is the height of the cylinder:

Surface Area = 2π (r² + rh)

PYRAMIDS AND CONES

Volume

Once you are comfortable with finding the volume of a prism, finding the volume of a pyramid is very simple: Calculate the volume as though the figure is a prism; then divide by 3.

Volume of a Pyramid

The volume of any pyramid is the area of the base, multiplied by the height of the pyramid.

Volume = × B × h

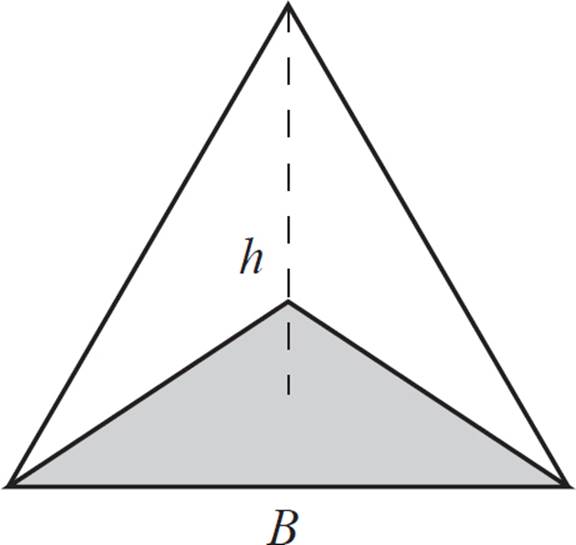
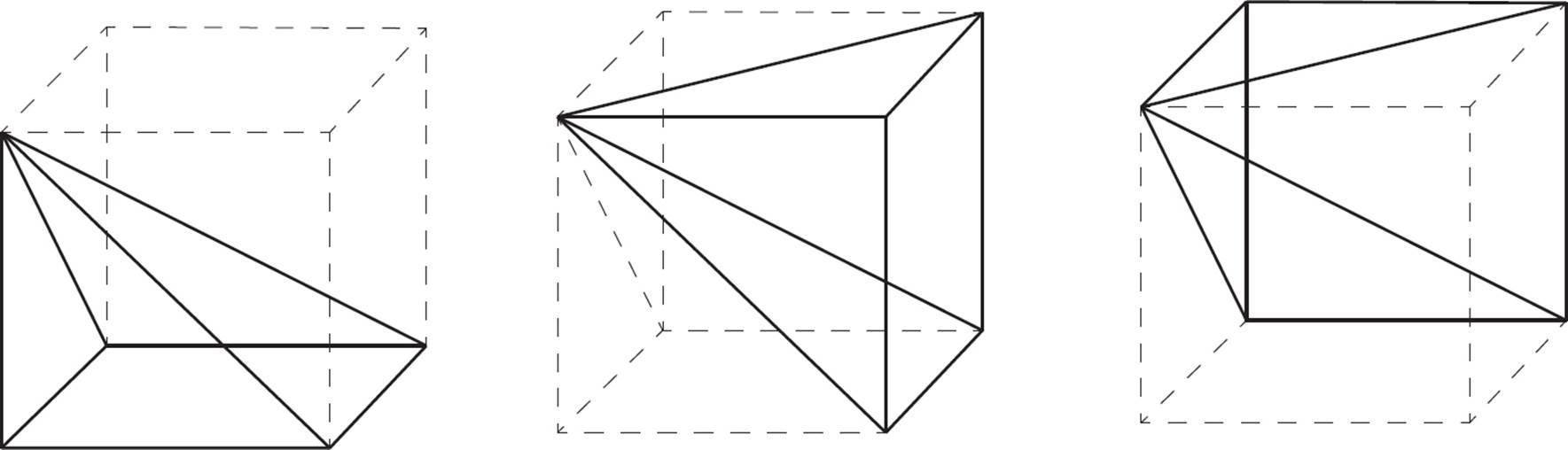
We can illustrate this relationship by combining three congruent pyramids to form a cube.

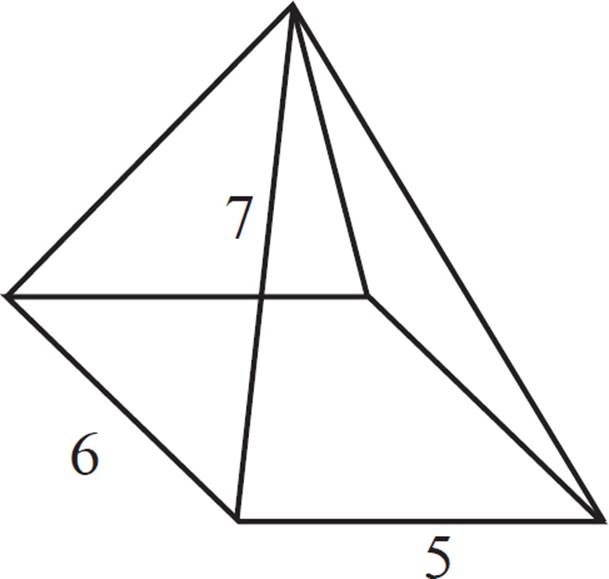
Find the volume of the rectangular pyramid shown above.

To calculate the volume of the pyramid, begin the same way you would if the figure were a prism—first, calculate the area of the base. Note that in a rectangular pyramid, the base is the rectangle, and all other faces are triangles. Calculate the area of the rectangular base:

A = 5 × 6

A = 30

Then, multiply that area by the height of the pyramid:

30 × 7 = 210

Then, divide by 3:

V =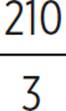

V = 70

To calculate the volume of a rectangular pyramid, you can use this formula:

Volume of a Rectangular Pyramid

Where l is the length, w is the width, and h is the height of the pyramid:

Volume = × l × w × h

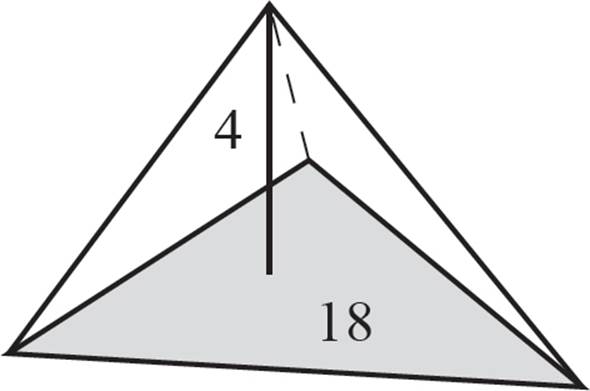
Find the volume of the triangular pyramid shown above.

In this example, the area of the base is already given, which simplifies things. In some other exercises, you would just need to calculate the area of the base first. Note that in a triangular pyramid, any of the faces can be considered the “base.” However, it’s important to remember that the height is perpendicular to the base, so make sure to calculate the height appropriately.

The area of the base is given:

A = 18

Multiply that area by the height of the pyramid:

18 × 4 = 72

Then, divide by 3:

V =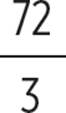

V = 24

Volume of a Cone

The process for calculating the volume of a cone is similar to that for a pyramid: Calculate the volume as though the figure is a cylinder; then divide by 3.

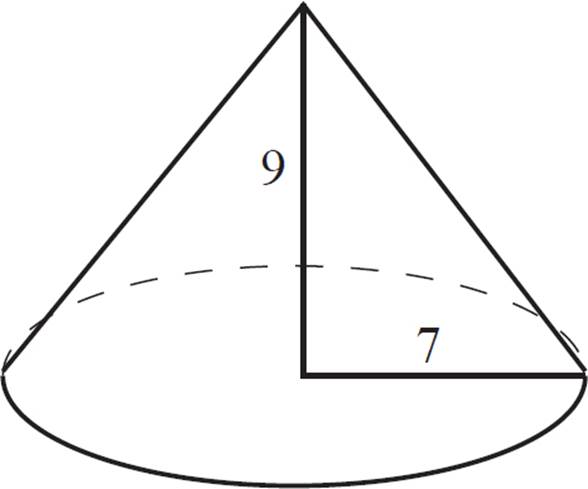
Find the volume of the cylinder shown above.

To calculate the volume of the cone, use the same basic idea as with a prism: Calculate the area of the base, multiply that area by the height, and then divide by 3. First, calculate the area of the circular base:

A = πr²

A = π × 7²

A = 49π

Multiply that area by the height of the cone:

= 49 × π × 9

= 441π

Finally, multiply by :

V = 441 × π ×

V = 147π

From our calculations above, we can derive the following formula:

Volume of a Cone

Where r is the radius of the circular base, and h is the height of the cone:

Volume = × πr² × h

Surface Area

To calculate the surface area of a pyramid, the most straightforward thing to do is to calculate the area of every face.

Surface Area of a Pyramid

The surface area of any pyramid is the sum of the areas of all of its faces.

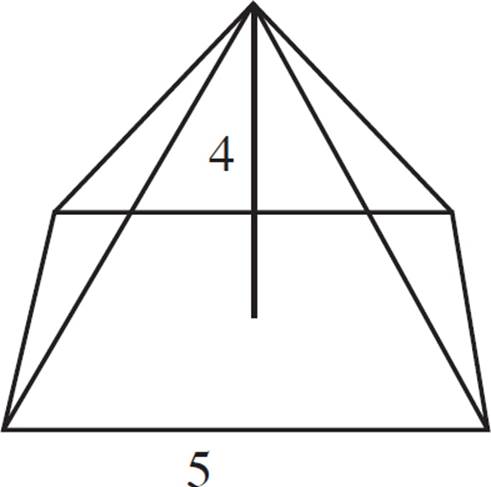
Find the surface area of the square, right pyramid shown above.

To calculate the surface area of the pyramid, calculate the areas of its faces. Start by calculating the area of the base:

A = 5 × 5

A = 25

Therefore, the area of the bottom face is 25.

Note that in a right regular pyramid, all of the triangular faces are congruent. Therefore, we just need to calculate one of them.

A = × 5 × 4

A = 10

Therefore, the triangular faces each have an area of 10.

Finally, add the areas of all the faces together:

SA = 25 + 10 + 10 + 10 + 10

SA = 65

Here is how you may see volume of a cone on the ACT.

The volume of a right circular cone with the bottom removed to create a flat base can be calculated from the following equation: V = πh(R² + r² + Rr) where h represents the height of the shape and R and r represent its radii as shown in the figure below:

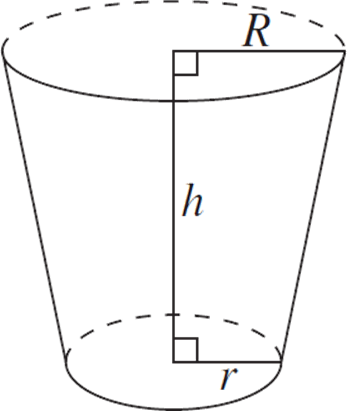
This formula can be used to determine the capacity of a large coffee mug. Approximately how many cubic inches of liquid can the cup shown below hold if it is filled to the brim and its handle holds no liquid?

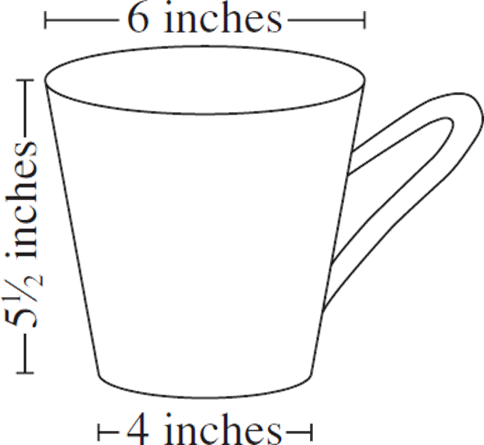
A.19

B.50

C.105

D.109

E.438

Surface Area of a Cone

Surface Area of a Cone

Where r is the radius and s is the slant height of the cone:

SA = πr² + πrs

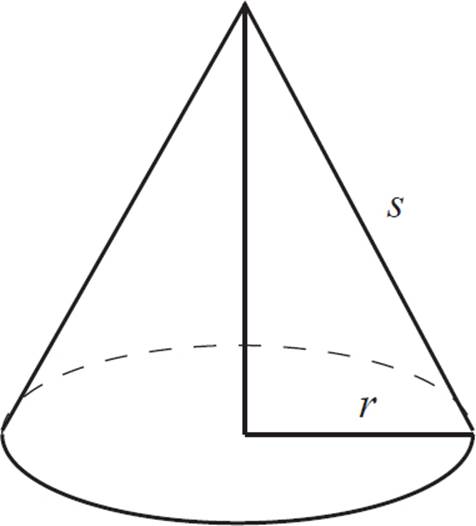
The formula for surface area of a cone is derived from the relationship between two circles. If you cut a cone open and flatten it out, you would have a portion of a circle:

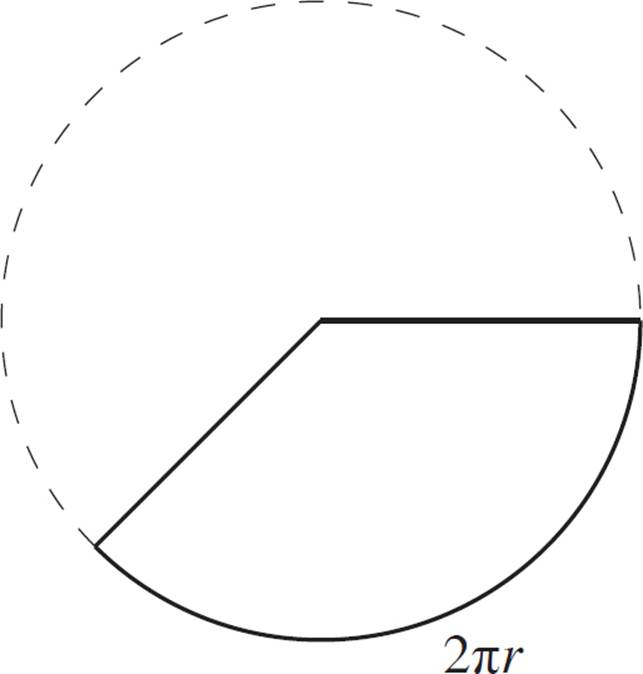
If we know the radius and arc length of a portion of a circle, then we can calculate the area of the “sector” of the circle. You will learn more about arcs and sectors in Chapter 7.

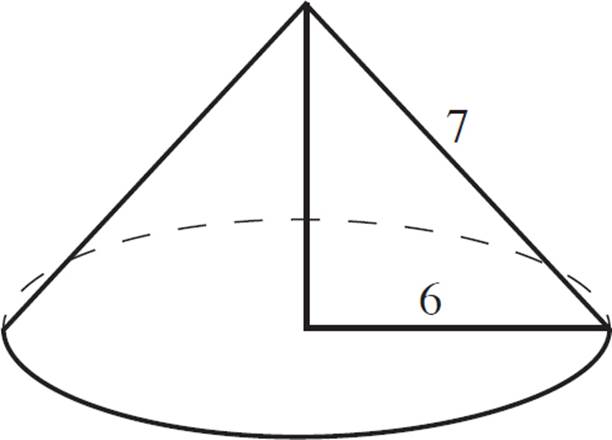
Find the surface area of the cone shown above.

Use the formula for the surface area of a cone:

SA = πr² + πrs

SA = π × 6² + π × 6 × 7

SA = π × 36 + π × 42

SA = π × (36 + 42)

SA = π × 78

The second figure shows that the small and large diameters of the coffee cup are 4 and 6, respectively, so the radii are 2 and 3. Plugging the numbers into the equation given, V = π5.5(3² + 2² + 3 · 2) = π5.5(19) ≈ 109. Choice (A) is the portion of the equation inside the parentheses, and (C) neglects to multiply by π. Choice (B) uses a height of instead of 5, or 5.5. Choice (E) plugs the diameters into the equation instead of the radii. The correct answer is (D).

POLYHEDRA

Since polyhedra can be all different shapes and sizes, there is no simple formula to apply to every one. Volume for a polyhedron is usually calculated by breaking up the figure into pyramids, and calculating the volume of each pyramid.

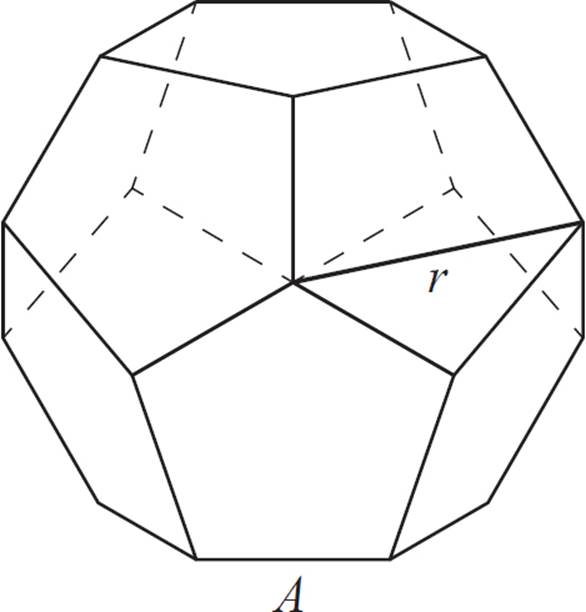
The figure above is a regular dodecahedron, with radius r and each face having area A. Find the volume area of the dodecahedron shown above.

Since regular polyhedra rarely have nice round numbers for both the side lengths and radius, this example is provided using variables. Here’s how to work it.

First, consider each face as having a pyramid apex at the center of the figure. Such a pyramid would look like this:

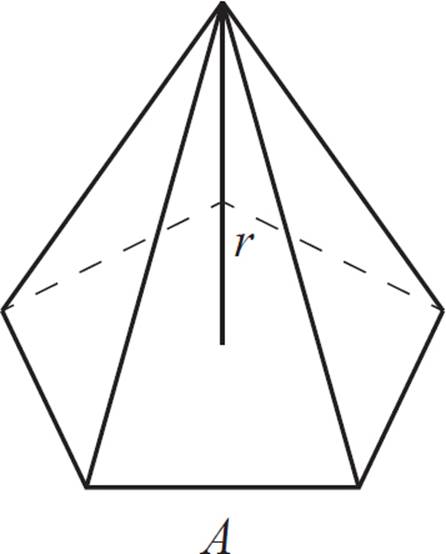
To calculate the volume of this pyramid, we would use the formula V = Bh. Substitute the variables from the figure to calculate the volume of each pyramid:

V = Ar

Since this is a regular polyhedron, you know that each face would form such a pyramid that is congruent to the one above. Therefore, the volume of this dodecahedron is

V = Ar × 12

V = 4 Ar

SPHERES

Volume of a Sphere

Where r is the radius:

V = πr³

Find the volume of a sphere with radius 6.

Use the formula for the volume of a sphere:

V = πr³

V = π × 6³

V = π × 216

V = 288π

Surface Area of a Sphere

Where r is the radius:

A = 4πr²

The Greek philosopher
Archimedes discovered
this formula over two
thousand years ago,
when he theorized
that the surface
area of a sphere is
equal to that of its
inscribed cylinder.

Find the surface area of a sphere with radius 8.

Use the formula for the surface area of a sphere:

A = 4πr²

A = 4 × π × 64

A = 256π

To see how spheres
are tested on the
SAT, access your
Student Tools online.

ANSWERS TO CHAPTER 5 EXERCISES

CARD Exercise

Prism Exercise

Where a is the altitude of the triangle, b is the base of the triangle, c and d are the other two sides of the triangle, and h is the height of the prism:

SA = ab + bh + ch + dh

DRILL

CHAPTER 5 PRACTICE QUESTIONS

Directions: Complete the following problems as specified by each question. For extra practice after answering each question, try using an alternative method to solve the problem or check your work.

Click here to download a PDF of Chapter 5 Practice Questions.

1. A square is inscribed in a circle with an area of 64π. What is the area of the square?

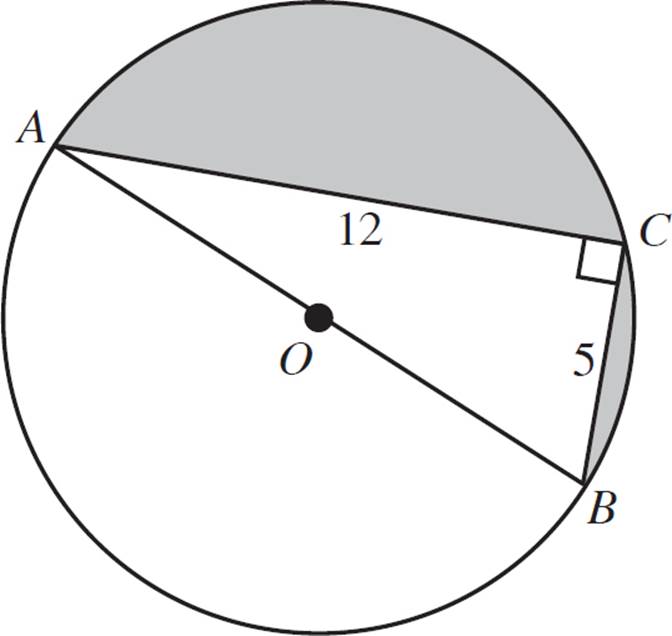
2. In the figure below, triangle ABC is inscribed in the circle with center O. What is the area of the shaded region?

3. What is the radius of a cylinder with a volume of 108π and a height of 3?

4. What is the surface area of the cylinder described in question 3?

5. A pyramid has a volume of 40 cubic units and a base area of 20. What is the pyramid’s height?

6. A hexagonal prism is composed of six identical equilateral triangular prisms. If the base of each triangular prism has an area of 12 cm² and the height of the hexagonal prism is 20 cm, what is the volume of the hexagonal prism?

7. Marcus wants to make himself an ice cream cone. He plans to pack the ice cream into the cone, filling it completely, and then add a scoop on top. If the cone has radius of 2 inches and a height of 6 inches and his ice cream scoop can make a spherical scoop with a radius of 3 inches, how many cubic inches of ice cream total does Marcus need?

8. Maria has constructed a square pyramid for a school project. She plans to cover the sides and base of the pyramid with contact paper. If the pyramid has a side length of 8 inches on the base and a slant height of 10 inches, how many square inches of contact paper will Maria need?

SOLUTIONS TO CHAPTER 5 PRACTICE QUESTIONS

1. 128

First draw the figure:

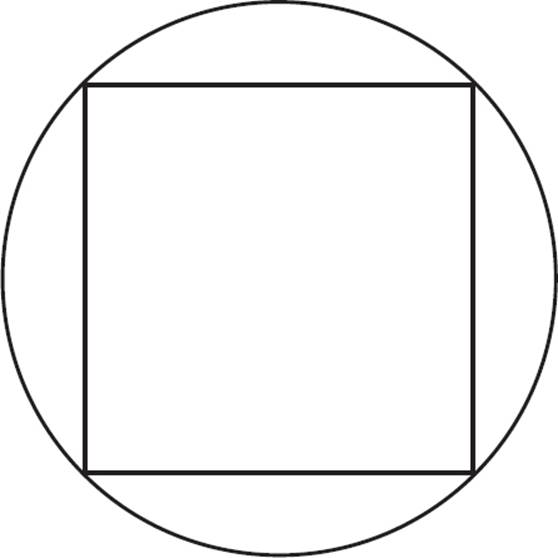
Knowing the area of the circle makes it possible to find the radius. Use the formula A = πr² and fill in 64π = πr². The π cancels out so r² = 64 and r = 8. No radius of the circle is entirely relevant to the square, but the diameter is. Draw a diameter that is a diagonal of the square.

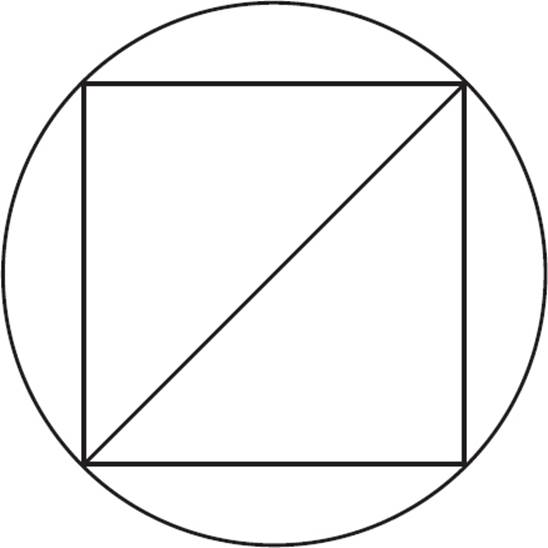
That diameter has a length of 16 since the radius is 8. That is also a diagonal of a square. Since a square has equal sides, we can use the Pythagorean theorem: x² + x² = 16². Now 2x² = 256, x² = 128, so x = , or 8. That is the side of the square. The question asks for the area of the square, which is × = 128. It is also possible to solve using the 45-45-90 triangle instead of the Pythagorean theorem.

2. 21.125π − 30 or about 36.366.

First, identify the shaded region. It is half of the circle minus the triangle. So we will need to find the area of the circle, divide that by 2, and then subtract the area of the triangle. Start by finding the area of the circle, for which the radius or diameter is needed. The diameter is the third side of the triangle. Use the Pythagorean theorem to find that the third side is 13 (or remember 5:12:13). That is the diameter, so the radius is half of 13, which is 6.5. Plug that into the area formula A = πr² to get A = 42.25π. That is the whole circle, so half of the circle has an area of 21.125π. Now find the area of the triangle. The base is 5 and the height is 12, so the formula is A = 1/2(5)(12) = 30. Thus, the area of the shaded region is 21.125π − 30.

One other strategy is to make a second right triangle to form one rectangle with length 12 and width 5. Find the area of the circle, subtract the area of the rectangle, and then divide by 2.

3. 6

Use the volume formula V = B × h. The base is a circle, so its formula is πr². Thus, the full volume formula for a cylinder is V = πr²h. In this case, it is 108π = πr²3. Cancel out the π: 108 = 3r². Divide by 3: 36 = r². Square root both sides to get r = 6.

4. 108π

The cylinder has a radius of 6 and height of 3. First, the surface area includes the top and bottom faces which are circles. Use the formula A = πr² to determine that each of the circles has an area of 36π for a total of 72π. The other part of the surface area is a rectangle with a length that is the circumference of the base and a height that is the height of the cylinder. Using the formula C = 2πr, the base has a circumference of 12π. Thus, the area of the rectangle is A = l × w = 12π × 3 = 36π. The total surface area is 72π + 36π = 108π. You can also use the formula Surface Area = 2π(r² + rh).

5. 6

Use the volume formula for a pyramid, which is V = 1/3 × B × h. Substitute the information provided: 40 = 1/3 × 20 × h. Then simplify: 40 = 20/3h. Multiply both sides by 3 to get 120 = 20h. Finally, divide by 20 to get h = 6.

6. 1440 cm³

Find the volume of each triangular prism using the formula V = B × h. The area of the base is 12 and the height is 20, so the formula is V = 12(20) = 240. That is for each triangular prism, so multiply by 6 to find that the total volume is 1440 cm³.

7. 44π

Since the question asks about cubic inches, it’s a volume problem. First, find the volume of the cone using the formula V = 1/3πr²h. The radius is 2 and the height is 6, so that is V = 1/3π(2²)(6) = 1/3π(4)(6) = 1/3π(24) = 8π. Now find the volume of the sphere using the formula V = 4/3πr³. The radius is 3, so the formula is V = 4/3π(3³) = 4/3π(27) = 36π. The total volume is 8π + 36π = 44π cubic inches.

8. 224

Since the question involves square inches and “covering” something, it is a surface area problem. Find the surface area of the pyramid. Start with the base, which is a square, so its formula is A = s². The side is 8, so the area of the base is 64. A square pyramid also has four equal triangular faces. Use the formula A = 1/2bh. The base is 8 and the height is 10, so the formula is A = 1/2(8)(10) = 40. That is just for one triangular face, so multiply by 4 to find the total area for the triangular faces: 160. Now add the 64 square inches from the bottom to get a total of 224 square inches.

REFLECT

Congratulations on completing Chapter 5!

Here’s what we just covered.

Rate your confidence in your ability to:

•Solve for area, circumference, radius, and diameter of a circle

•Find the incenter and circumcenter of a polygon

•Find the area or radius of a circle inscribed in a polygon, and vice versa

•Know the five types of regular polyhedra

•Understand cross-sections of prisms, spheres, cylinders, pyramids, and cones

•Know how to find volume and surface area of prisms, spheres, cylinders, pyramids, and cones

If you rated any of these topics lower than you’d like, consider reviewing the corresponding lesson before moving on, especially if you found yourself unable to correctly answer one of the related end-of-chapter questions.

Access your online student tools for a handy, printable list of Key Points for this chapter. These can be helpful for retaining what you’ve learned as you continue to explore these topics.