High School Geometry Unlocked (2016)

Lesson 6.2. Distance and Midpoint

In this lesson, we’ll review how to calculate the distance and midpoint from two points in the coordinate plane. You’ll also learn how to divide a line to a certain ratio, such as 1:3.

DISTANCE

The distance between two coordinates is the measure of the length between them. In the coordinate plane, you’ll determine distance by using calculations, rather than a measuring tool such as a ruler.

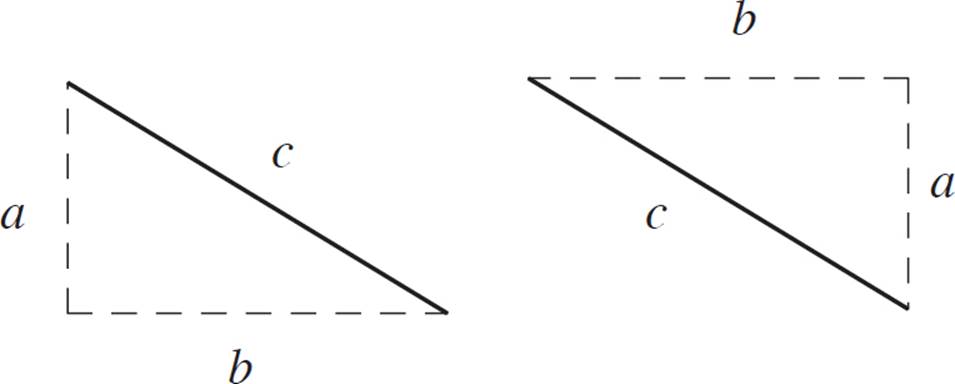
One straightforward way to calculate distance is to use the Pythagorean theorem. In other words, you can construct a right triangle in which the two points form the hypotenuse. Then, use the Pythagorean theorem to find the length of the hypotenuse.

There are two ways that you can draw such a right triangle from two points—think of it like two halves of a rectangle. It does not matter which way you draw the triangle, because both are rotations of each other and are therefore congruent. The hypotenuse will be the same either way.

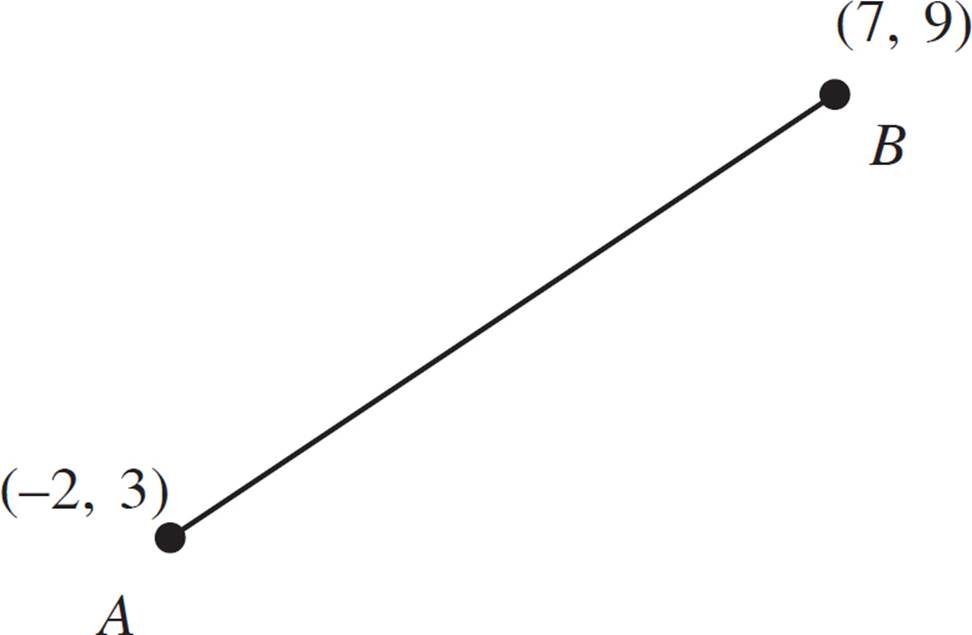
Find the length of AB.

First, make a right triangle from the figure. Extend a horizontal line from one of the two points, and a vertical line from the other, to where they intersect.

In order to solve this problem, first put line n into slope-intercept form by adding 8x to both sides and then dividing both sides by 4. This will result in y = 2x + 6. You now know that the slope of line n is 2 and the y-intercept is 6. Since you also know they-intercept of line m as it is given in point (0, 8), you know these are not the same lines. Eliminate (D).

To determine whether or not (C) will be the answer, find the slope of line m by using the slope formula:

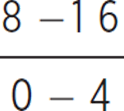slope = 2

Since both lines m and n have a slope of positive 2, they are parallel and will never intersect. Thus, (C) is correct.

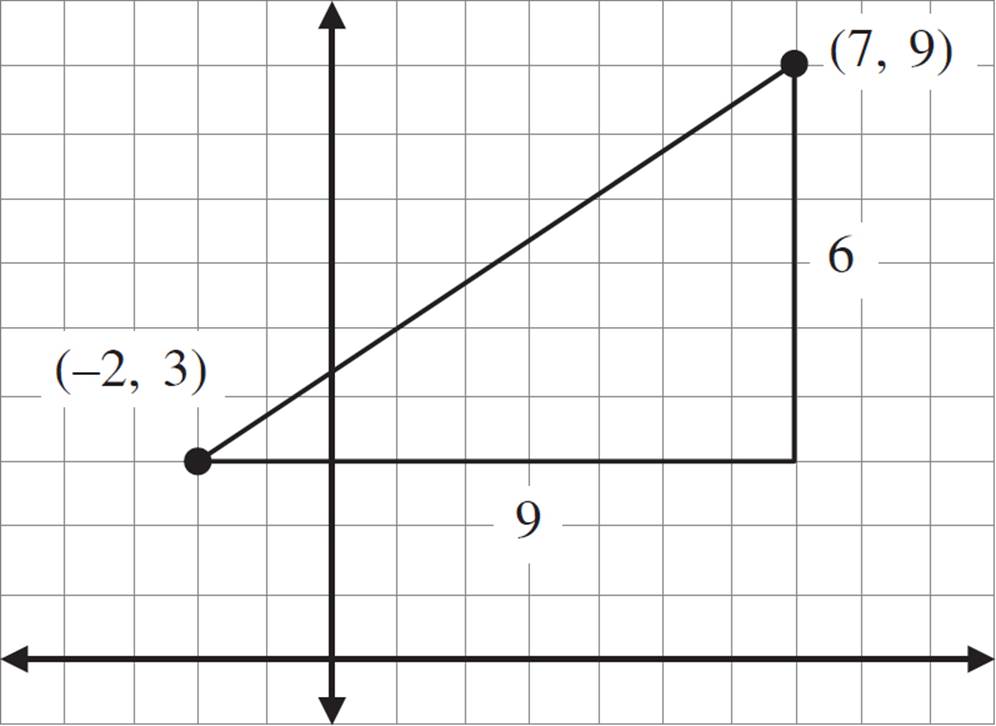
You can measure the legs of this triangle by counting, or by subtracting the x and y coordinates, respectively. The legs of this triangle are 6 and 9, as shown in the figure above.

Then, use the Pythagorean theorem to solve for the hypotenuse:

a² + b² = c²

6² + 9² = c²

36 + 81 = c²

 117 = c²

= c

The length of AB is , or ≈ 10.82.

Distance Formula

For the distance
formula, you do not
have to worry about
the order of (x₁ − x₂)
versus (x₂ − x₁)—since
you end up squaring
these values, the result
will always be positive.

The distance formula is derived from the Pythagorean theorem.

First, if we take the square root of both sides of the equation, we “solve” for c:

a² + b² = c²

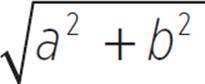= c

We can also substitute for a and b using the coordinates of the two points:

a = x₁ − x₂

b = y₁ − y₂

Substitute those values for a and b, respectively:

c =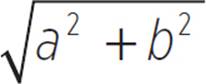

c =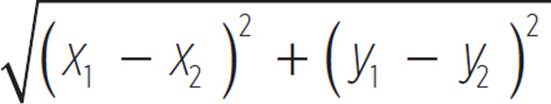

That’s the distance formula—or, you could call it “Pythagorean Theorem in the Coordinate Plane.”

Distance Formula

To find the distance d between two points (x₁, y₁) and (x₂, y₂):

d =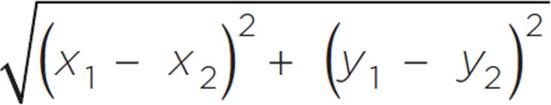

Here is how you may see coordinate distance on the ACT.

What is the perimeter of quadrilateral STUR if it has vertices with (x, y) coordinates S (0, 0), T (2, −4), U (6, −6), R (4, −2) ?

F. 2

G. 2 + 2

H. 8

J. 80

K. 400

Try plugging the points from the previous example, (2, 3) and (7, 9), into the distance formula:

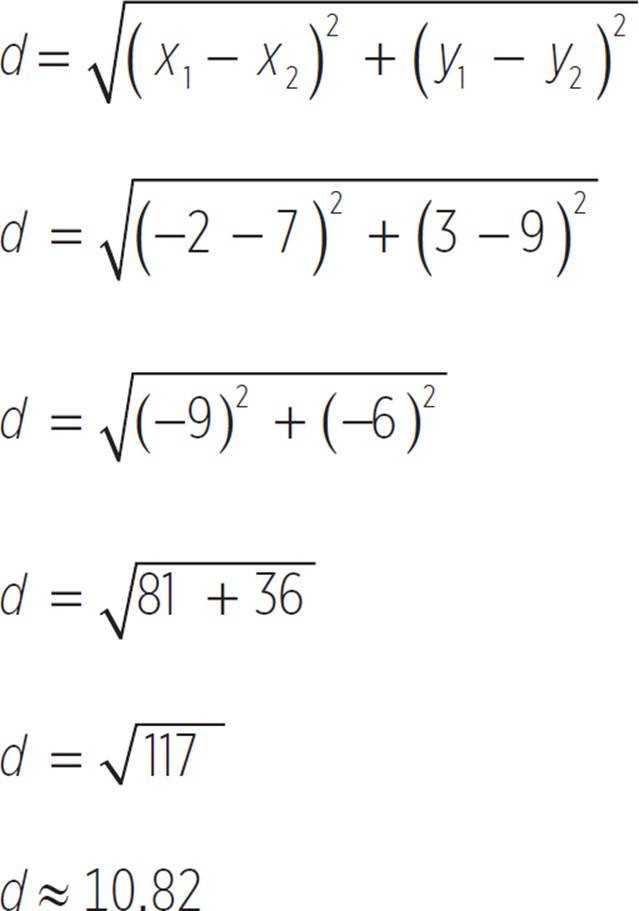
This is the same result that we got when we used the Pythagorean theorem.

Memorizing the distance formula may help make your calculations easier, but either method is valid.

MIDPOINT

The midpoint of two coordinates is the point that lies exactly halfway between them.

Consider what you do when you need to find the “midpoint” of two numbers—you just take the average of the two numbers. For example, we know that 6 is exactly halfway between 2 and 10, because 6 is the average of 2 and 10: 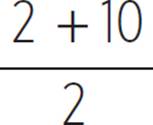= 6.

To find the midpoint between two coordinates, you’re essentially doing the same thing—finding the average of the numbers. The difference is that there are two pairs of numbers instead of one. More specifically, you’re finding the average of the x-coordinates and then the average of the y-coordinates.

Another way to think about midpoint is “the point that is halfway between the two x-values, and halfway between the two y-values.”

Find the midpoint of AB.

To calculate the midpoint between these coordinates, find the average of the x-values; then find the average of the y-values.

The average of the x-coordinates is 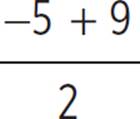, which equals 2. This is the x-coordinate of the midpoint.

The average of the y-coordinates is 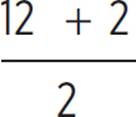, which equals 7. This is the y-coordinate of the midpoint.

Therefore, the midpoint is (2, 7).

Start by plotting out the figure to determine the distance between each point. You can find the distance between each point by using the distance formula: d 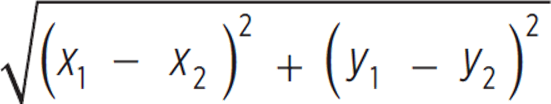. From point S to point R, for example, find d 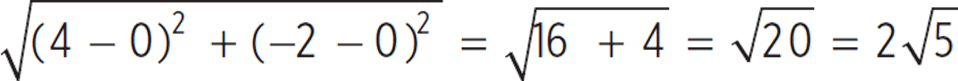. As you compare the other sides, you’ll notice that they all equal 2, so the perimeter will be 4 × 2 = 8. The correct answer is (H).

Midpoint Formula

The Midpoint Formula is derived from taking the average of the x- and y-coordinates, respectively.

Midpoint Formula

To find the midpoint m between two points (x₁, y₁) and (x₂, y₂):

midpoint =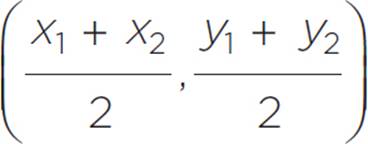

DIVIDING A SEGMENT TO A CERTAIN RATIO

Sometimes, instead of finding the midpoint, you’ll need to divide a line segment to a different ratio, such as 1:3 or 2:5. For these exercises, we can perform the same procedure as with a dilation.

If you need to
review dilations, see
Chapter 3 of this book.

Here is how you may see midpoint on the ACT.

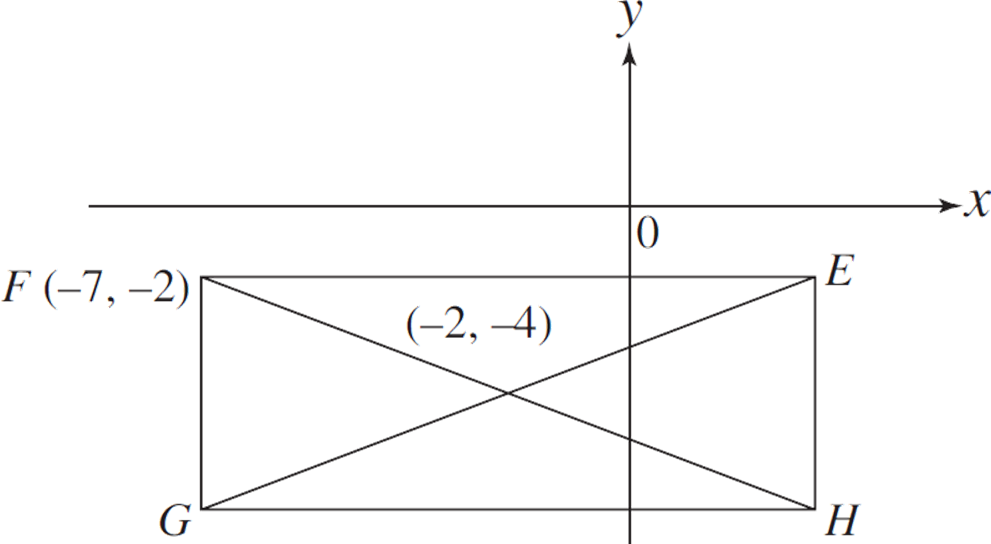
As shown below, the diagonals of rectangle EFGH intersect at the point (−2, −4) in the standard (x, y) coordinate plane. Point F is at (−7, −2). Which of the following are the coordinates of H ?

F.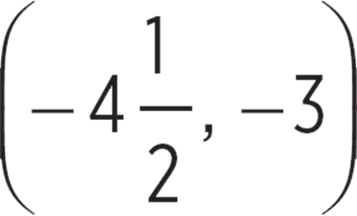

G. (−7, −6)

H. (3, −2)

J. (3, −6)

K. (−5, 3)

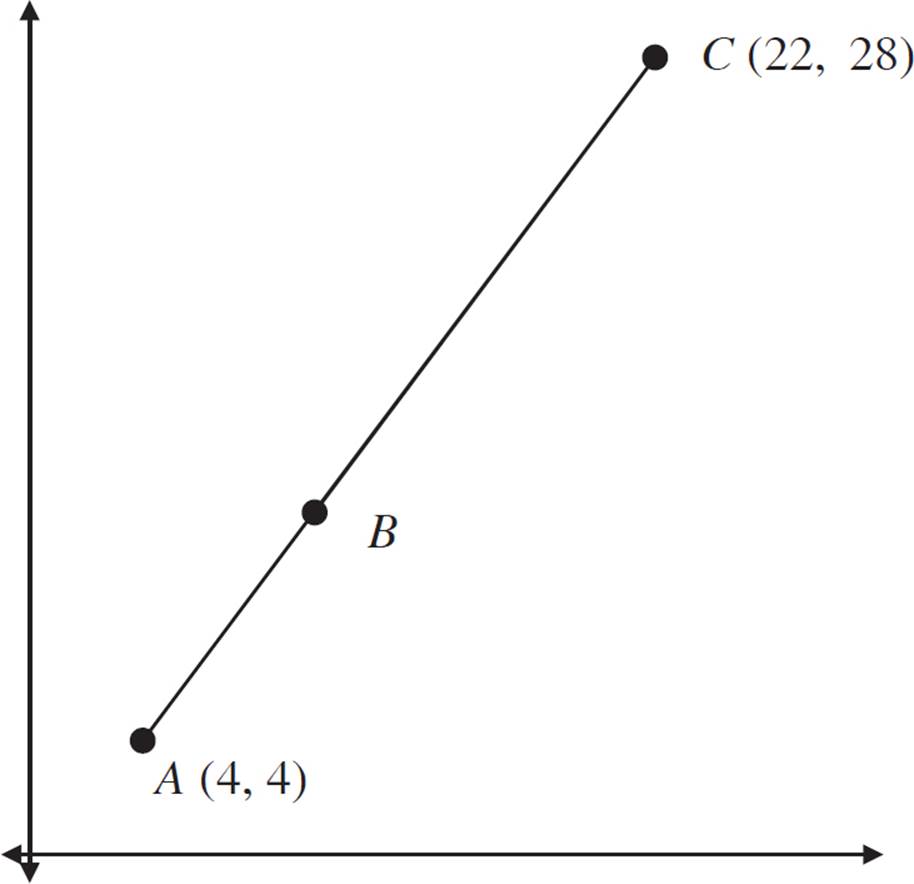
In the figure above, the ratio of AB to BC is 1:2. Find the coordinate for point B.

This example uses a ratio. Recall that ratios are a part-to-part relationship, while fractions are part-to-whole. A ratio of 1:2 is equivalent to a fraction of . Another way to think about this ratio is with an algebraic expression for each length:

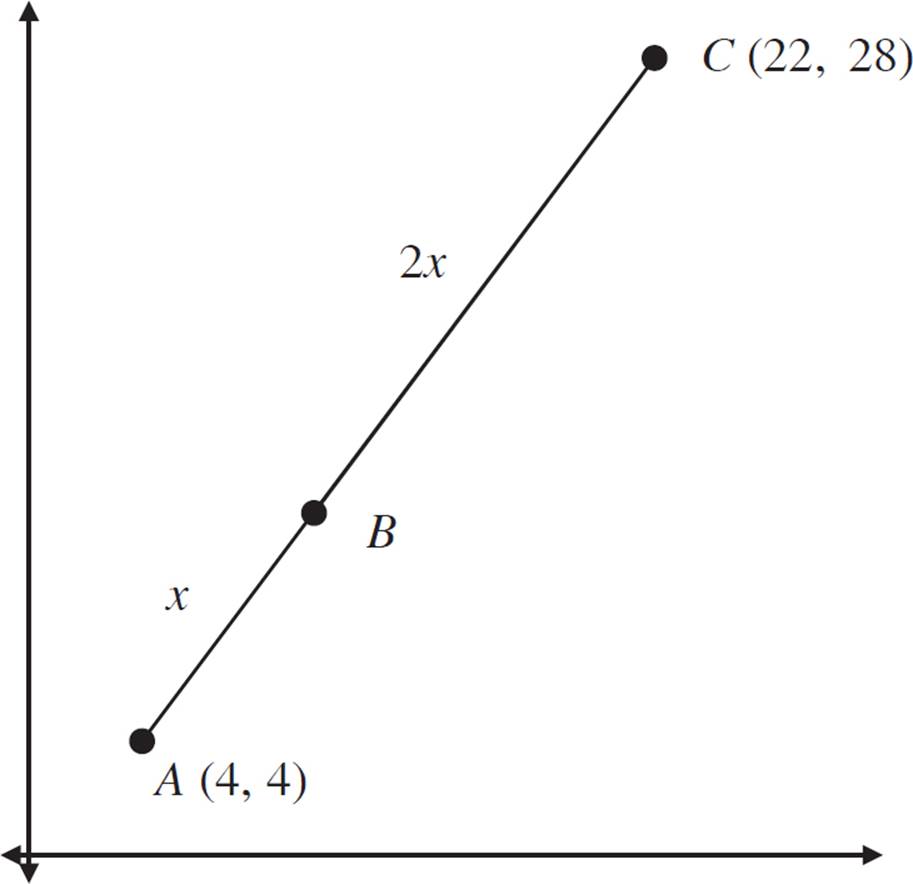
If AB has a length of x, then BC has a length of 2x. The total length of AC would be x + 2x, or 3x. That means that x is of the total length 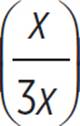, while 2x is of the total length .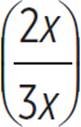

Treat this exactly like a dilation, with point A as the center of dilation, and the scale factor as .

Recall the formula for a dilation:

Dilation of a Coordinate

Where (x₁, y₁) is the center of dilation, and s is the scale factor, the dilated version of coordinate (x₂, y₂) is:

(x₁ + s(x₂ − x₁), y₁ + s(y₂ − y₁))

To perform the dilation of point C, plug in (4, 4) as (x₁, y₁) and plug in (22, 28) as (x₂, y₂). The scale factor is .

(x₁ + s(x₂ − x₁), y₁ + s(y₂ − y₁))

(4 + (22 − 4), 4 + (28 − 4)

(4 + (18), 4 + (24)

(4 + 6, 4 + 8)

(10, 12)

Point B is at (10, 12).

The point of intersection represents the midpoint between points F (−7, −2) and H (unknown). Note that the given midpoint is (−2, −4). You can use the midpoint formula, 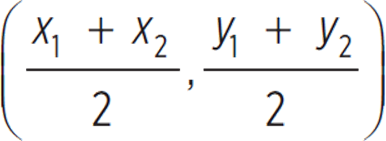to determine the coordinates of point H. Solving for the x-coordinate gives 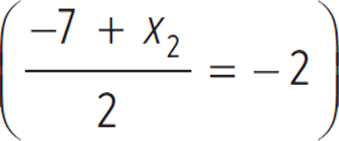. The x-coordinate of point H equals 3, eliminating (F), (G), and (K). Solving for the y-coordinate gives 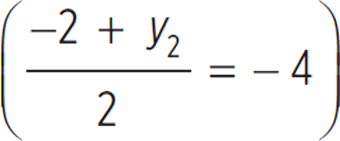. The y-coordinate of point H equals −6, eliminating (H). The correct answer is (J).

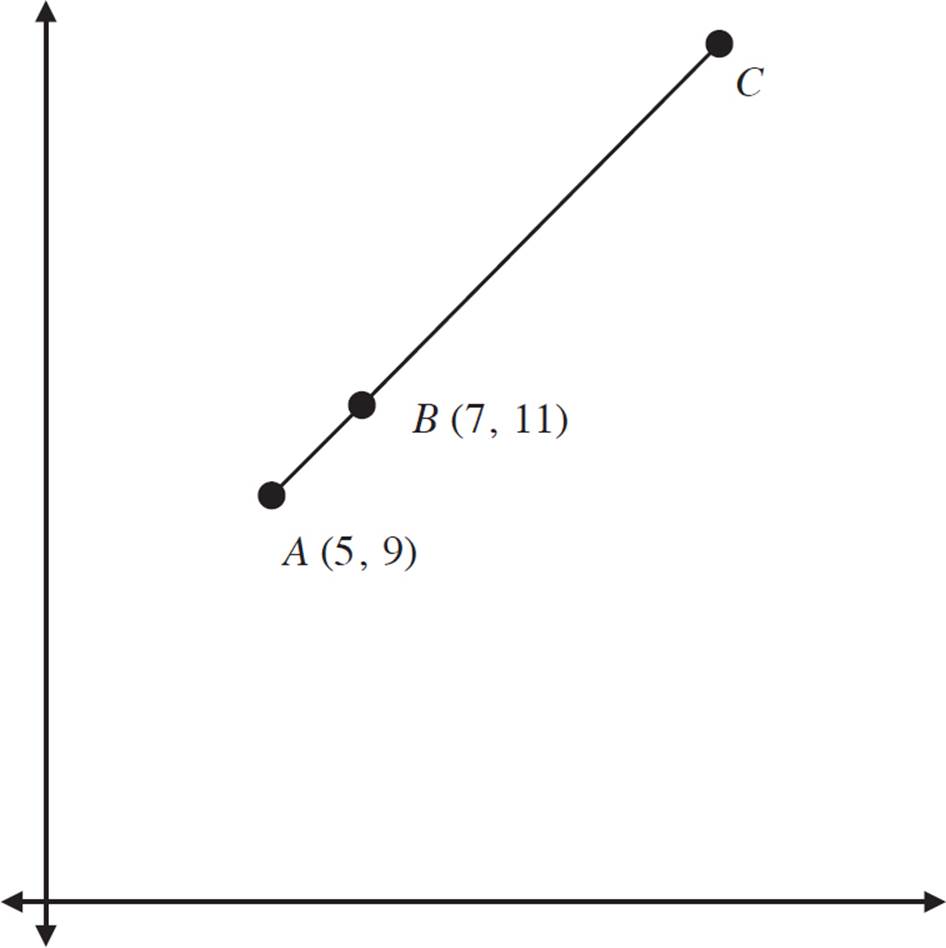
In the figure above, the ratio of AB to BC is 1:4. Find the coordinate for point C.

This example uses a ratio. To set this up as a dilation, first convert the ratio to a fraction. Add the two parts to get the denominator: 1 + 4 = 5 parts. A ratio of 1:4 is equivalent to a fraction of . In this case, it means that AC is 5 times longer than AB. Therefore, the scale factor is 5.

Treat this exactly like a dilation, with point A as the center of dilation, and the scale factor as 5.

To perform the dilation of point B, plug in (5, 9) as (x₁, y₁) and plug in (7, 11) as (x₂, y₂). The scale factor is 5.

(x₁ + s(x₂ − x₁), y₁ + s(y₂ − y₁))

(5 + 5 (7 − 5), 9 + 5 (11 − 9))

(5 + 5 (2), 9 + 5 (2))

(5 + 10, 9 + 10)

(15, 19)

Point C is at (15, 19).

Some ratio questions
refer to “internal” or
“external” division.
Internal division
means that the new
point will be between
the original two
points. (Example 9
does this). External
division means that
the new point will
form a longer version
of the original line
segment. (Example
10 does this).