High School Geometry Unlocked (2016)
Chapter 7. Circles
Lesson 7.3. Slices of Pi
In this lesson, you will learn how to calculate an arc/sector based on information about a circle, and vice versa. You will also learn how to use radians, which are units of angle measure.
Normally, the easiest way to think about these problems is in terms of basic fractions—that is, part/whole relationships. Imagine that you have a pizza with 8 congruent slices. If you eat 1 of the slices, then you know that you ate ![]() of the total pizza.
of the total pizza.
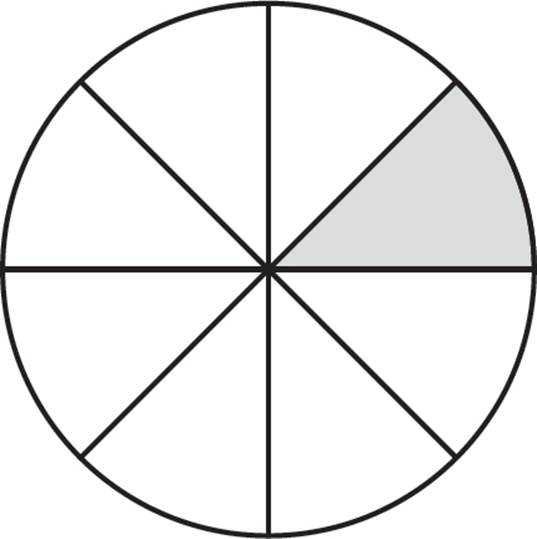
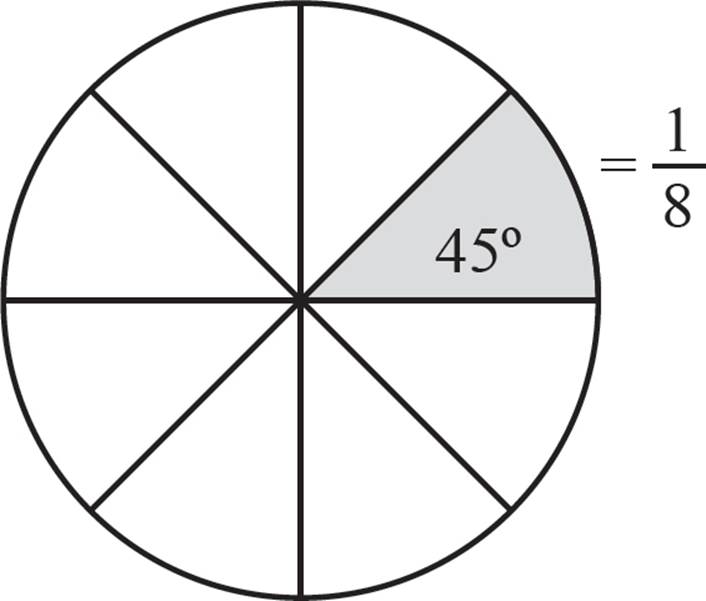
Now, if you wanted to know the degree measure of the missing pieces of pizza, that is also fairly straightforward. Since we know that the total degree measure of a circle is always 360°, we can use a proportion to find the angle of the sector. This is a part/whole relationship—the measure of the arc, compared with the measure of the full circle.
|
|
|
|
1 × 360° = 8 × x |
Cross-multiply. |
|
360° = 8 × x |
|
|
|
Divide both sides of the equation by 8. |
|
45° = x |
Therefore, the total degree measure of the missing pieces is 45°.
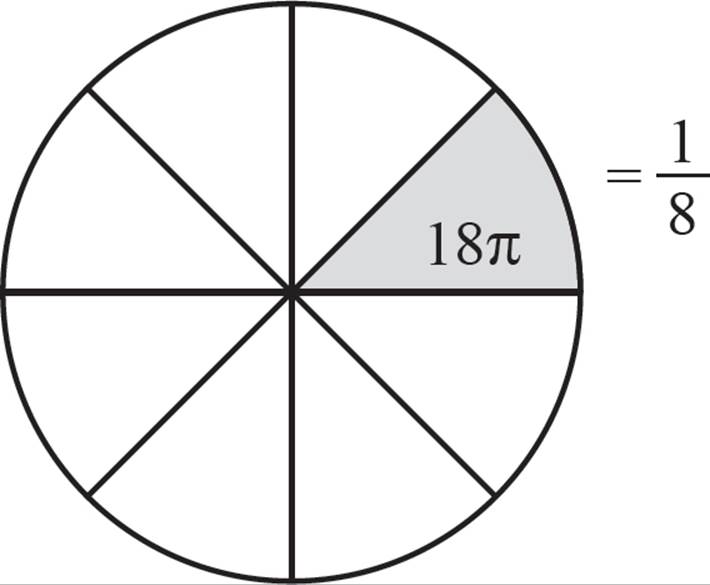
What if you wanted to know the total area of the 1 slice you ate? To do that, you would use another part/whole relationship—the area of the slice, compared with the total area of the pizza. So, you would need some information about the size of the pizza. Let’s say that you’re told that the radius of the circle is 12 inches. That would be enough to tell you the area of the full pizza:
r = 12
A = πr2
= π(12)2
= 144π
Therefore, the area of the pizza is 144π square inches. Now, we can use a proportion to find the area of the sector.
|
|
|
|
1 × 144π = 8 × x |
Cross-multiply. |
|
144π = 8 × x |
|
|
|
Divide both sides of the equation by 8. |
|
18π = x |
Simplify. |
Therefore, the total area of the missing pieces is 18π square inches.
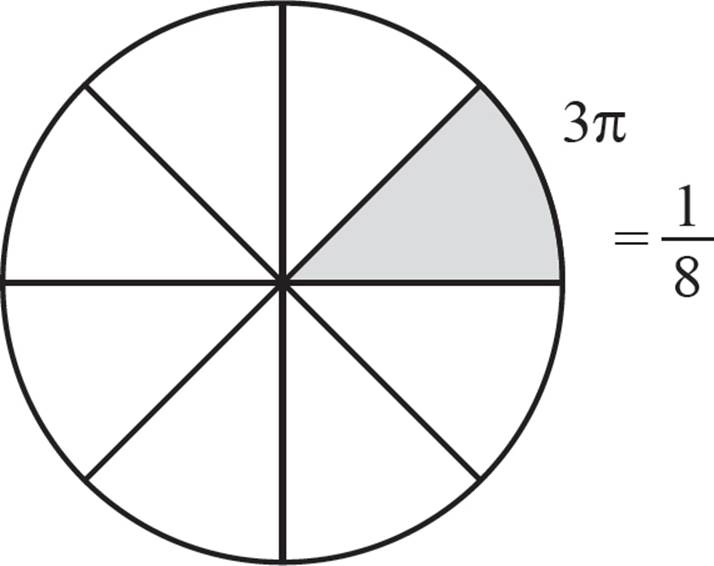
Let’s calculate the length of the arc (because obviously, the crust is the best part). To do that, we’ll use another part/whole relationship—the length of the arc from the slices, compared with the total circumference of the pizza. We were told that the radius of the circle is 12 inches. With that, we can calculate the circumference of the pizza:
|
r = 12 |
|
|
C = 2πr |
|
|
= 2π(12) |
|
|
= 24π |
Simplify. |
Therefore, the circumference of the pizza is 24π inches. Now, we can use a proportion to find the length of the arc.
|
|
|
|
1 × 24π = 8 × x |
Cross-multiply. |
|
24π = 8 × x |
|
|
|
Divide both sides of the equation by 8. |
|
3π = x |
Simplify. |
Therefore, the length of the arc for the missing pieces is 3π inches.
To solve a problem with arc or sectors, remember that all of the following are proportional:
Parts of a Circle
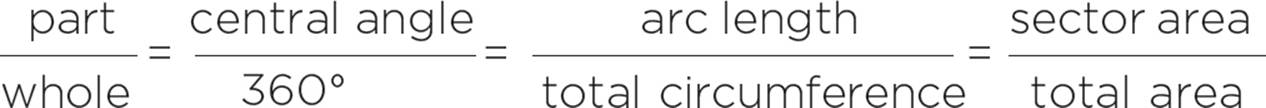
You can solve for all of these parts if you have only two: something that tells you the size of the full circle, and something that tells you the size of the wedge.

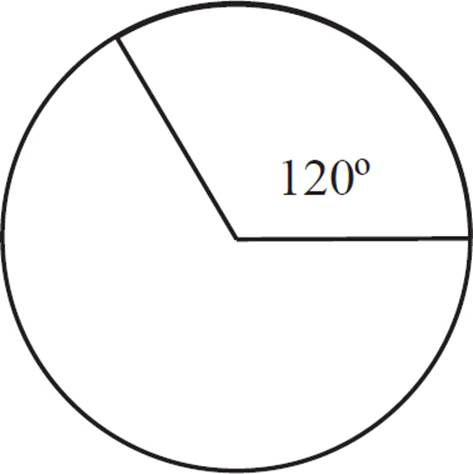
In the figure above, the circle has a radius of 9. What is the area of the sector with a central angle of 120°?
With the radius given, you can solve for the area of the circle:
A = πr2
= π(9)2
= 81π
You also know the angle measure of the sector, so to set up a proportion:
|
|
|
|
|
Simplify. |
|
1 × 81π = 3 × x |
Cross-multiply. |
|
81π = 3 × x |
|
|
|
Divide both sides of the equation by 3. |
|
27π = x |
Simplify. |
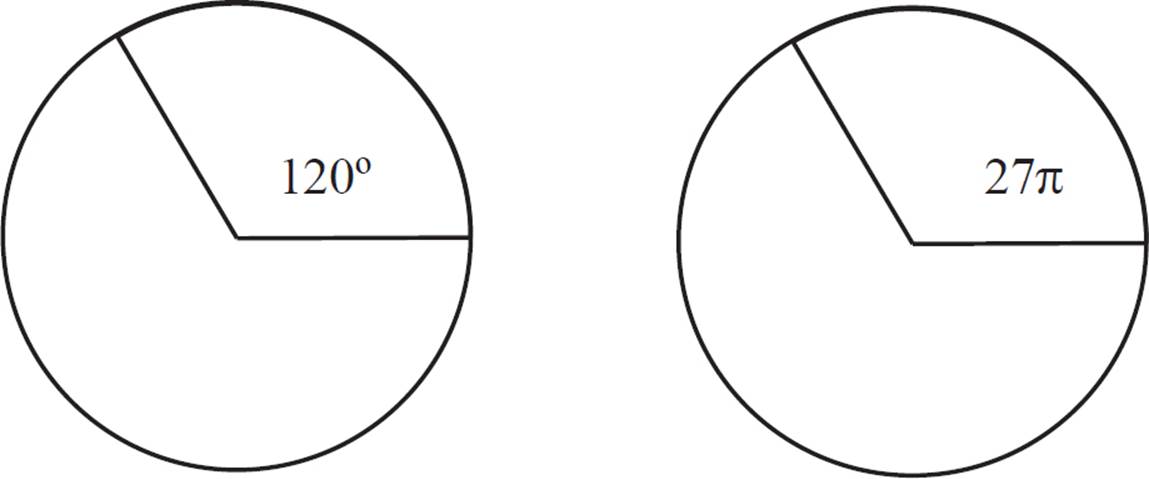
The area of the sector is 27π.


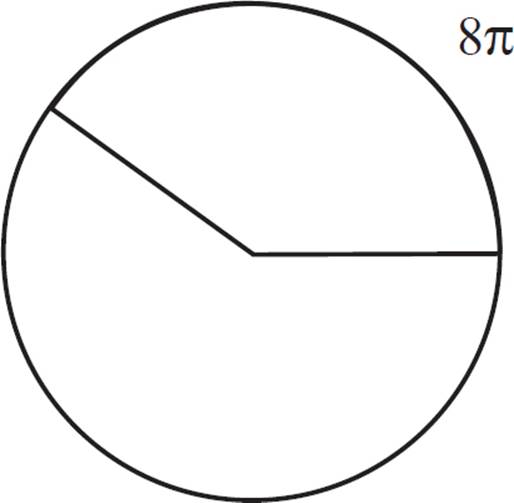
In the figure above, the circle has an area of 100π. What is the central angle of the arc with a length of 8π?
In this example, we’ll need to make a proportion that uses the fraction of arc length/circumference. But we weren’t given circumference, we were given area. No problem—we can use the area to solve for the radius, and then solve for the circumference.
|
A = πr2 |
|
|
100π = πr2 |
|
|
100 = r2 |
Divide both sides of the equation by π. |
|
10 = r |
Take the square root of both sides of the equation. |
With the radius known, we can solve for the circumference:
|
C = 2πr |
|
|
C = 2π(10) |
|
|
C = 20π |
Simplify. |
Now, set up a proportion to solve for the central angle of the arc. On one side of the equation, use the given arc length with circumference.

Remember CARD
from Chapter 5;
you can solve for
circumference, area,
radius, and diameter
if you have just one
of those pieces of
information given.
|
|
|
|
|
Simplify. |
|
|
Simplify. |
|
2 × 360° = 5 × x |
Cross-multiply. |
|
720° = 5 × x |
|
|
|
Divide both sides of the equation by 5. |
|
144° = x |
Therefore, the degree measure of the arc is 144°.
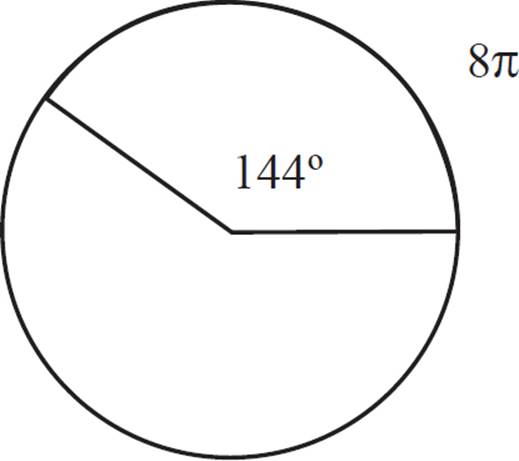


Here is how you may see arcs on the SAT.
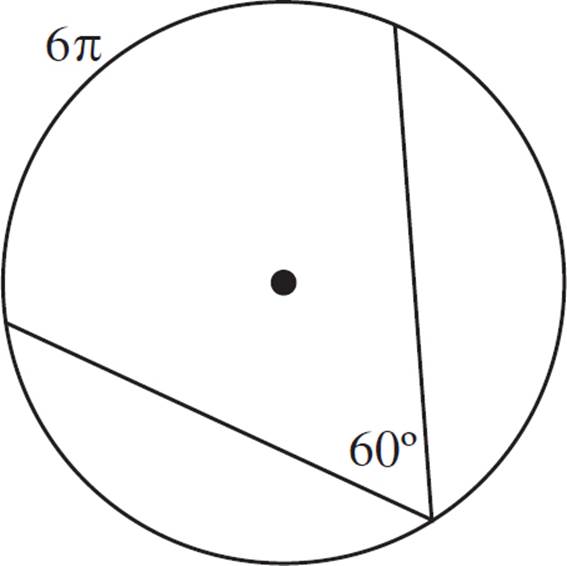
Points A and B lie on circle O as shown below. ∠BOA is 45°. If the area of circle O is 64π, what is the length of minor arc AB?
A. 2π
B. 4π
C. 8π
D.16π
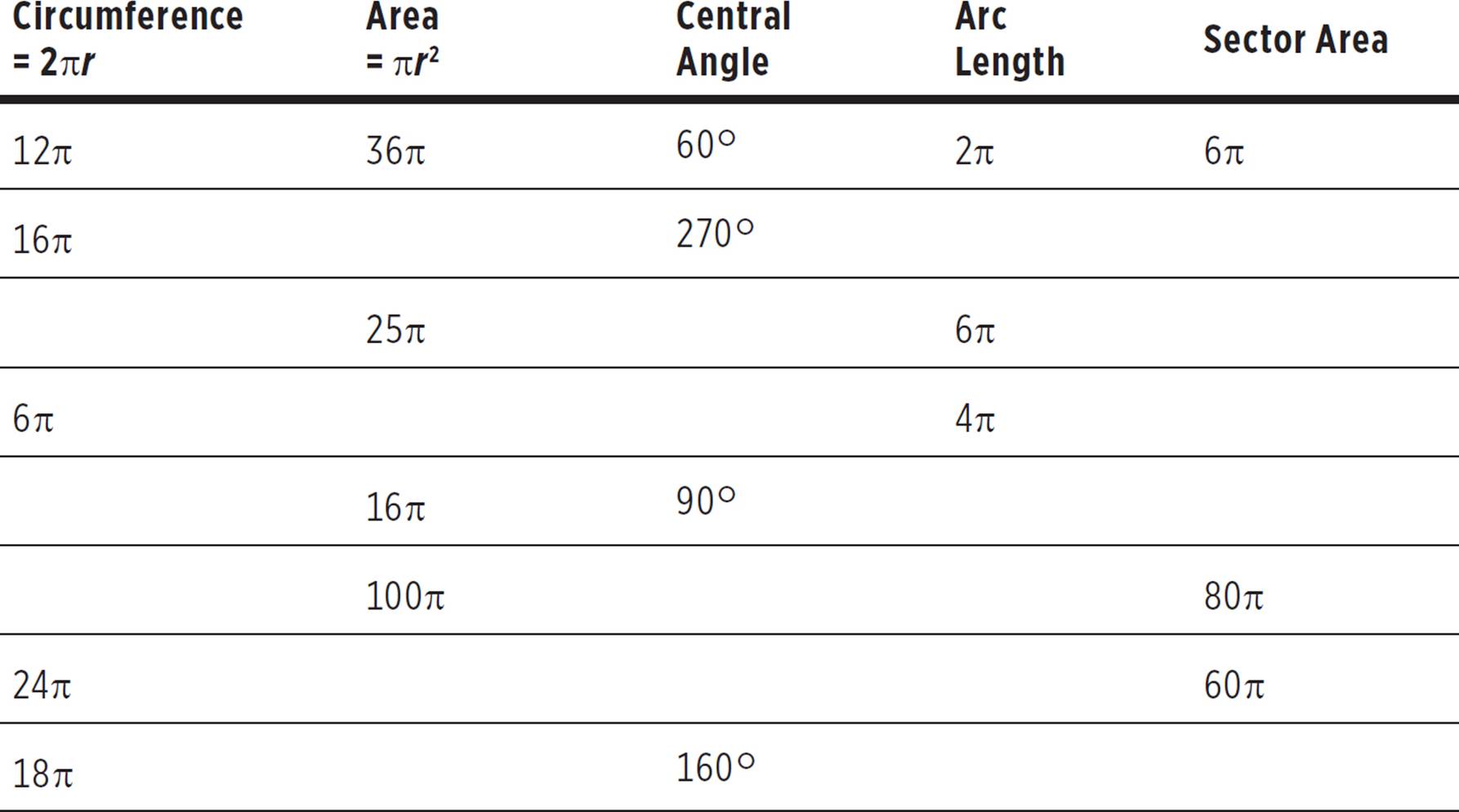
Pi Practice
Try completing the table below. Each row gives two pieces of information—something about the whole circle, and something about the arc or sector. For example, if area and central angle are given in a row, try solving for sector area first, then circumference and arc length. The first row has been completed.
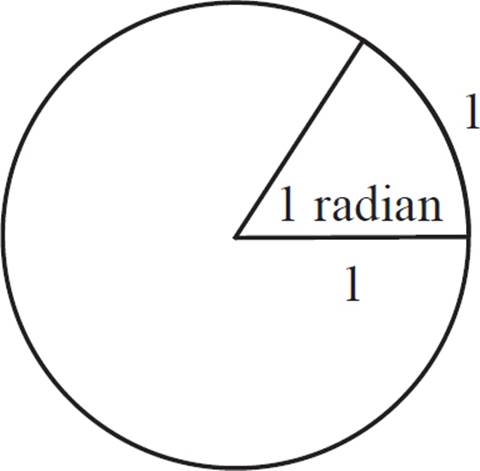
RADIANS
The radian is a unit of angle measure. One radian represents an angle in which the arc length is exactly equal to the radius of a circle. It is usually described in terms of a circle with a radius of 1. In a circle with a radius of 1, one radian corresponds to an arc with a length of 1.
Mathematicians like to
use radians, because
it is a unit based on a
“real” relationship in a
circle—the relationship
between the arc and
the radius. Degrees, by
contrast, are actually
arbitrary units. The
reason we use 360°
is because 360 has a
lot of factors, which
makes division easy.
A circle has precisely 2π (≈ 6.283) radians, a measure equal to 360°. Angles measured in radians are best expressed as fractions of 2π. For example, a half circle has an angle measure of π radians (= ![]() of 2π), and a quarter circle has an angle measure of
of 2π), and a quarter circle has an angle measure of ![]() radians (=
radians (= ![]() of 2π).
of 2π).
If you see an angle
measure expressed
in terms of π, you
can be sure that
you’re dealing with
radians. Sometimes,
the abbreviation
“r” is used, but it
is not necessary.

You know the area is 64π, so you can solve for the radius, which is 8. That makes the circumference 16π. Since ∠BOA is 45°, which is ![]() of the 360° of a circle, the length of arc AB will be
of the 360° of a circle, the length of arc AB will be ![]() of the circumference.
of the circumference. ![]() of 16π is 2π. The correct answer is (A).
of 16π is 2π. The correct answer is (A).
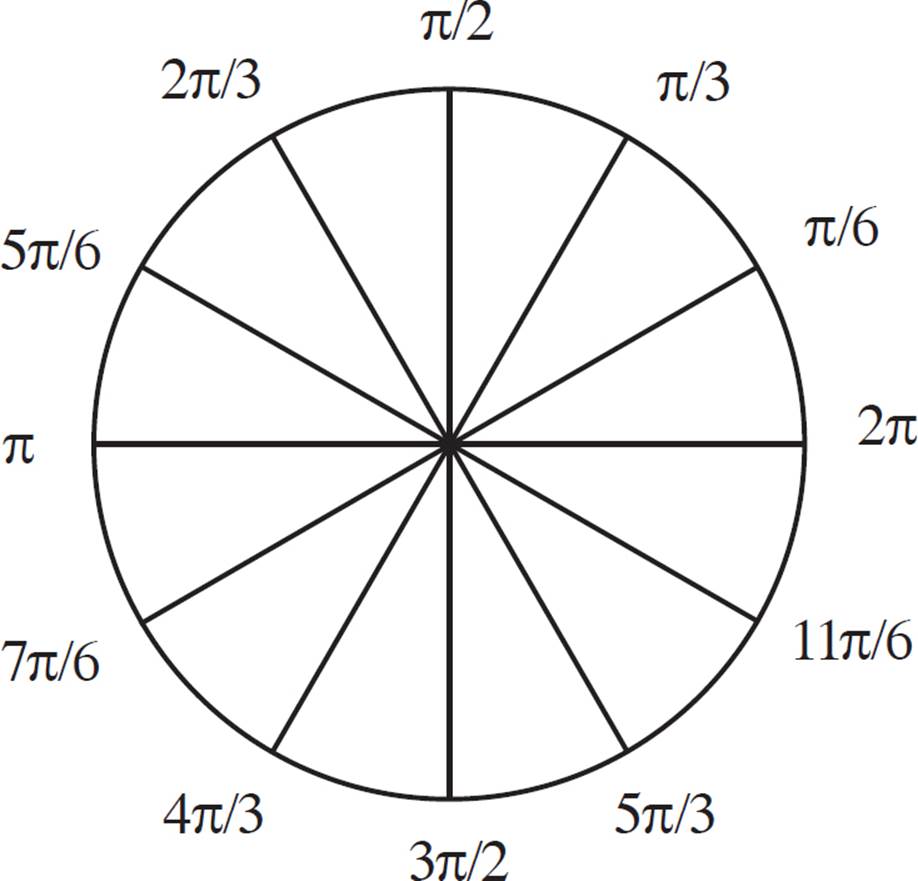
If the figure is confusing, it may help you to write down the unreduced form of each fraction, as a multiple of ![]() . For example,
. For example, ![]() is equal to
is equal to 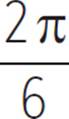 , and so on. You’ll see that the values are sequential;
, and so on. You’ll see that the values are sequential; ![]() ,
, 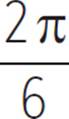 ,
,  , etc.
, etc.
To convert radians to degrees, or vice versa, use the following proportion:
Converting Radians and Degrees
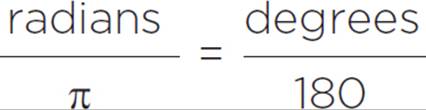

What is the equivalent of 216 degrees, as expressed in radians?
To convert degrees to radians, use the proportion above.
|
|
|
|
|
Simplify. |
|
|
Multiply both sides of the equation by π. |
The angle measure equivalent to 216 degrees is ![]() radians.
radians.


Here is how you may see radians on the ACT.
Which of the following degree measures is equivalent to 2.25π radians?
A.101.25
B.202.5
C.405
D.810
E.1,620
Radians Practice
Try the following conversions. Answers are at the end of this chapter.

ARCS AND SECTORS USING RADIANS
To solve a problem with arc or sector and radians, use the following proportions:
Parts of a Circle
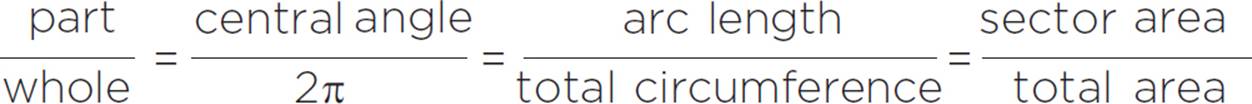

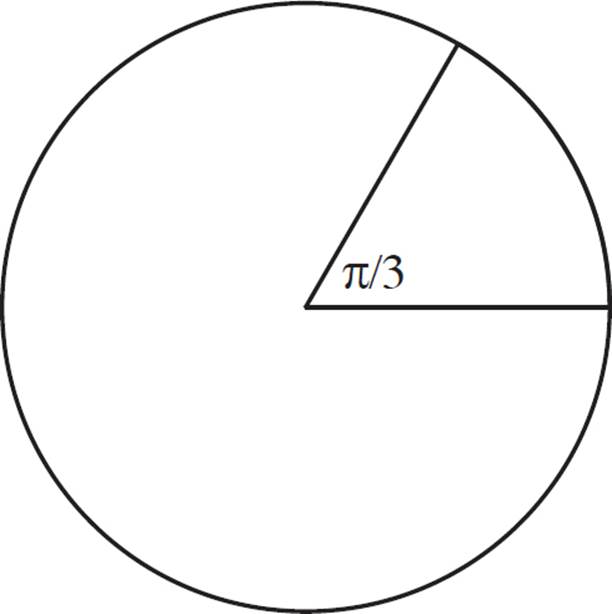
In the figure above, the circle has a circumference of 36π. What is the length of the arc with a central angle of ![]() ?
?
With the circumference and angle measure given, you can set up a proportion:
|
|
||
|
|
Simplify. |
|
|
|
Simplify. |
|
|
1 × 36π = 6 × x |
Cross-multiply. |
|
|
36π = 6 × x |
Don’t be afraid to
begin with nested
fractions in your
proportion. You can
simplify in the next
step. It’s better to get
everything down in the
format you know, first.

To change 2.25π radians into degrees, multiply by 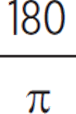 to get 405°. Choices (A) and (B) are fractions of 405. Choices (C) and (E) are multiples. The correct answer is (C).
to get 405°. Choices (A) and (B) are fractions of 405. Choices (C) and (E) are multiples. The correct answer is (C).
|
|
Divide both sides of the equation by 6. |
|
6π = x |
Simplify. |
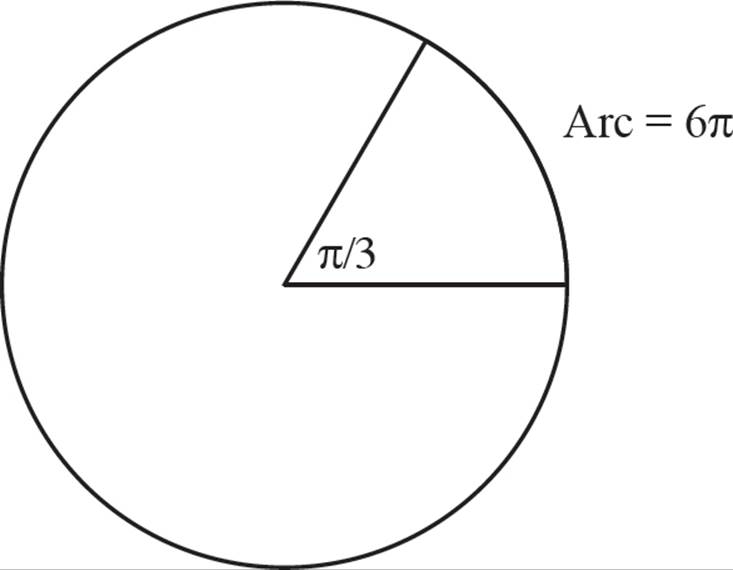
The length of the arc is 6π.


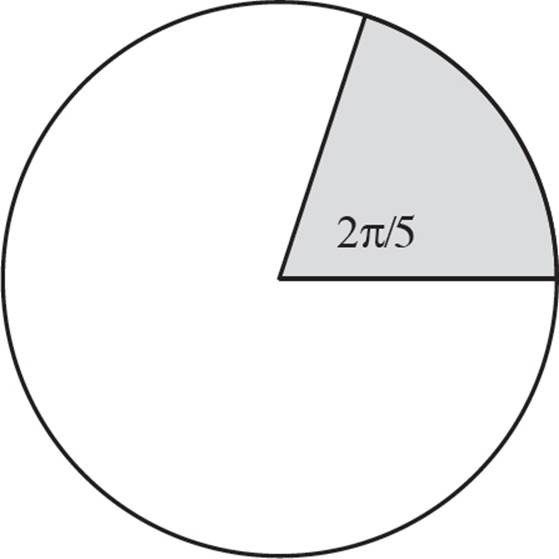
In the figure above, the circle has a radius of 5. What is the area of the sector with a central angle of ![]() ?
?
With the radius given, you can solve for the area of the circle:
A = πr2
= π(5)2
= 25π
You also know the angle measure of the sector, so set up a proportion:
|
|
|
|
|
Simplify. |
|
|
Simplify. |
|
1 × 25π = 5 × x |
Cross-multiply. |
|
25π = 5 × x |
|
|
|
Divide both sides of the equation by 5. |
|
5π = x |
Simplify. |
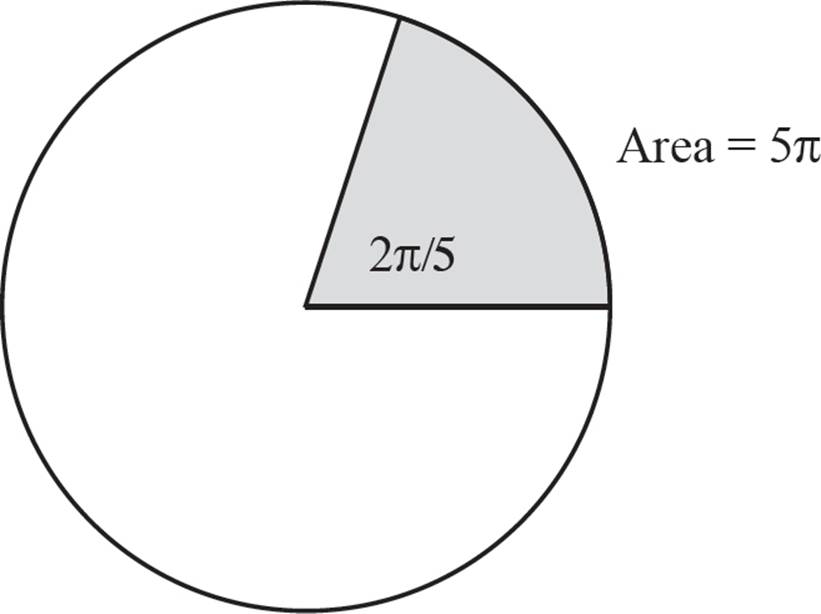
The area of the sector is 5π.

ANSWERS TO CHAPTER 7 EXERCISES
Pi Practice
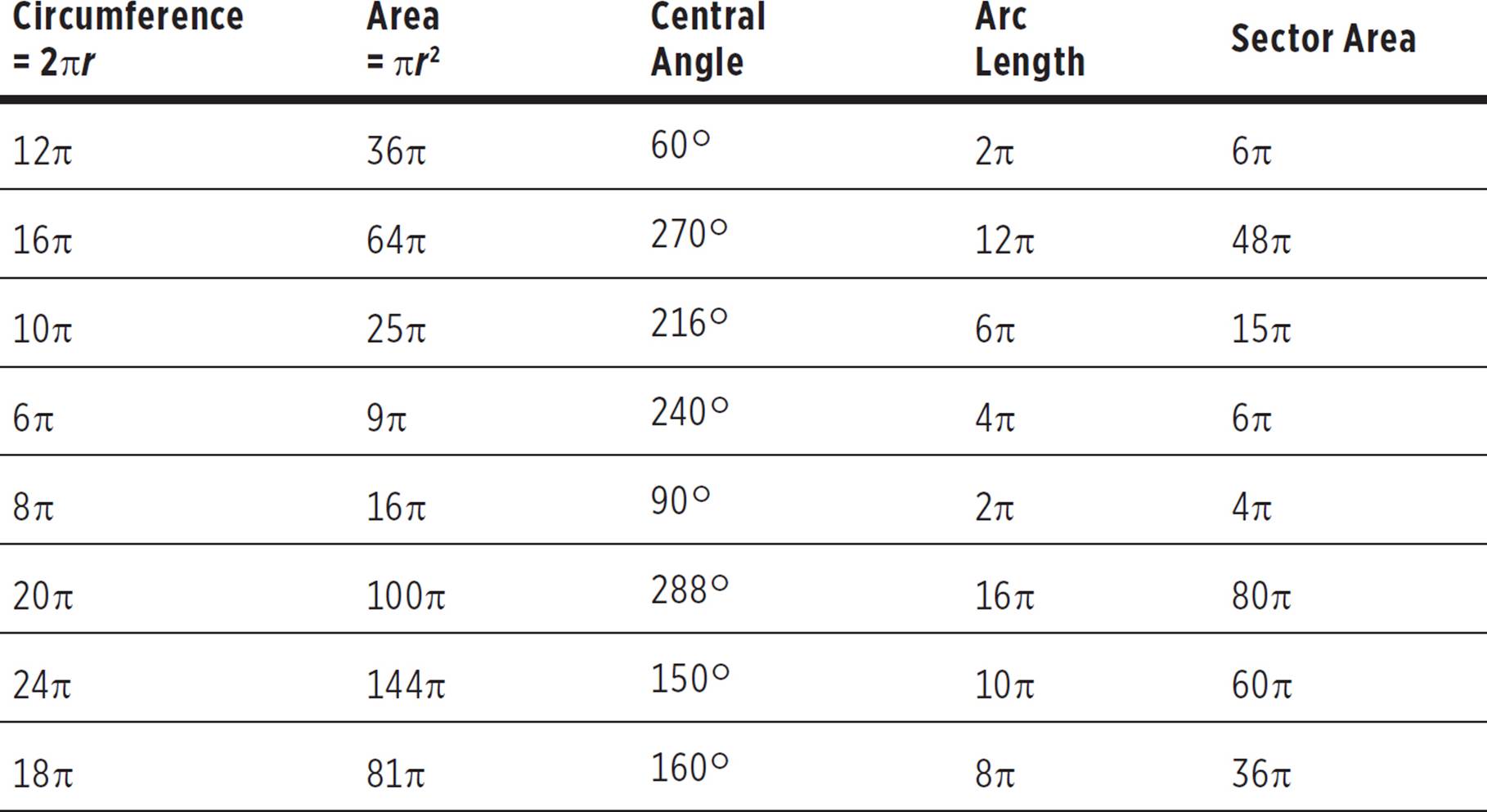
Radians Practice
DRILL
CHAPTER 7 PRACTICE QUESTIONS
Directions: Complete the following problems as specified by each question. For extra practice after answering each question, try using an alternative method to solve the problem or check your work.
Click here to download a PDF of Chapter 7 Practice Questions.
1.An angle measures 4 radians. What is the measure of the angle in degrees?
2.If the area of a circle is 9, what is the circumference?
3.In the figure below, what is the area of the circle?
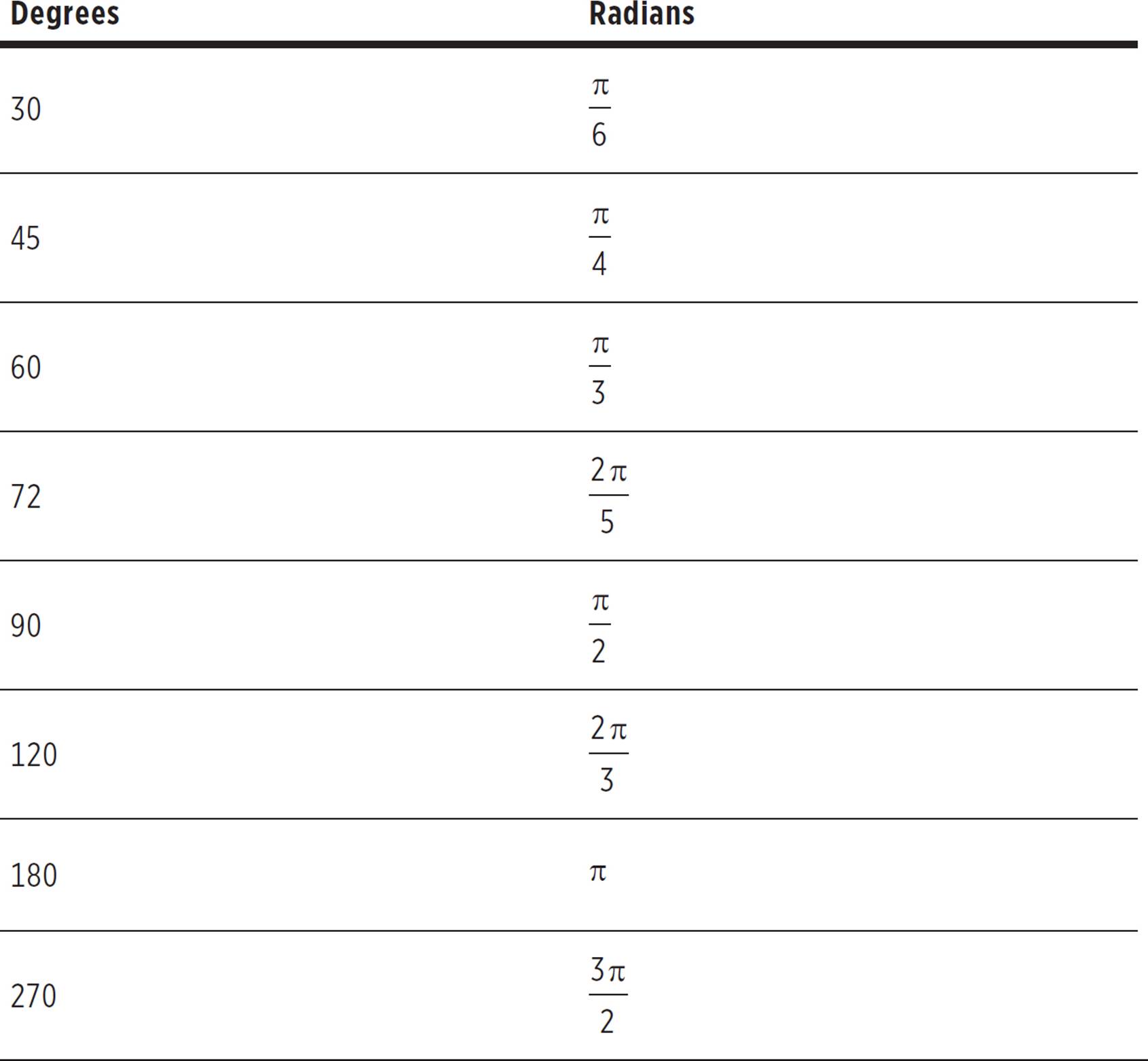
4.The circumference of the circle below is 12π and the center is O. If the area of the sector formed by AO, BO, and minor arc AB is 4π, what is the measure of ∠AOB in radians?
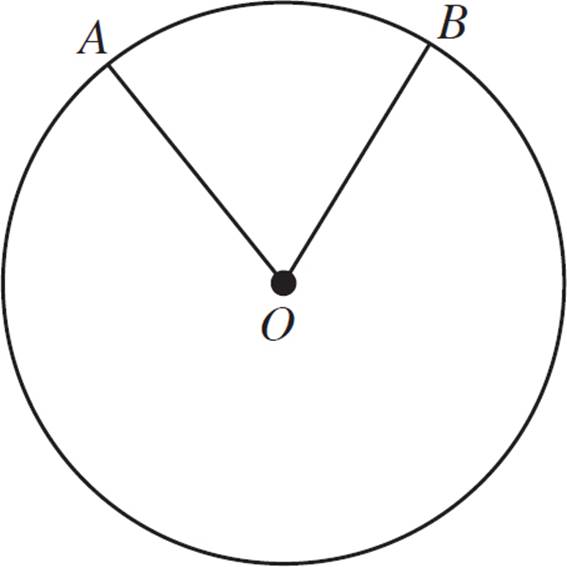
5.In the figure below, if the radius of the circle with center O is 4, what is the area of triangle PQR?
6.If the area of the annulus between two concentric circles is 64π and the ratio between the radii of the two circles is 5:3, what is the area of the larger circle?
7.In the figure below, both circles have center O and ∠AOC is ![]() radians. If two circles have circumferences 16π and 8π, respectively, what is the area of the shaded region?
radians. If two circles have circumferences 16π and 8π, respectively, what is the area of the shaded region?
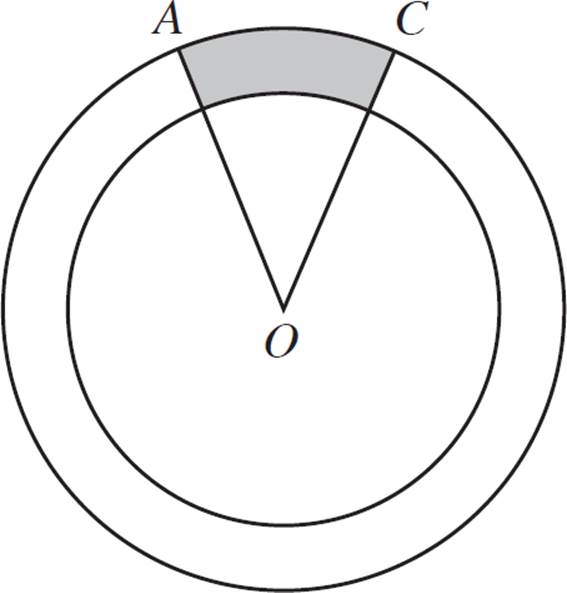
8.In the figure below, if the radius of the circle with center O is 1, what is the area of quadrilateral ABCO?
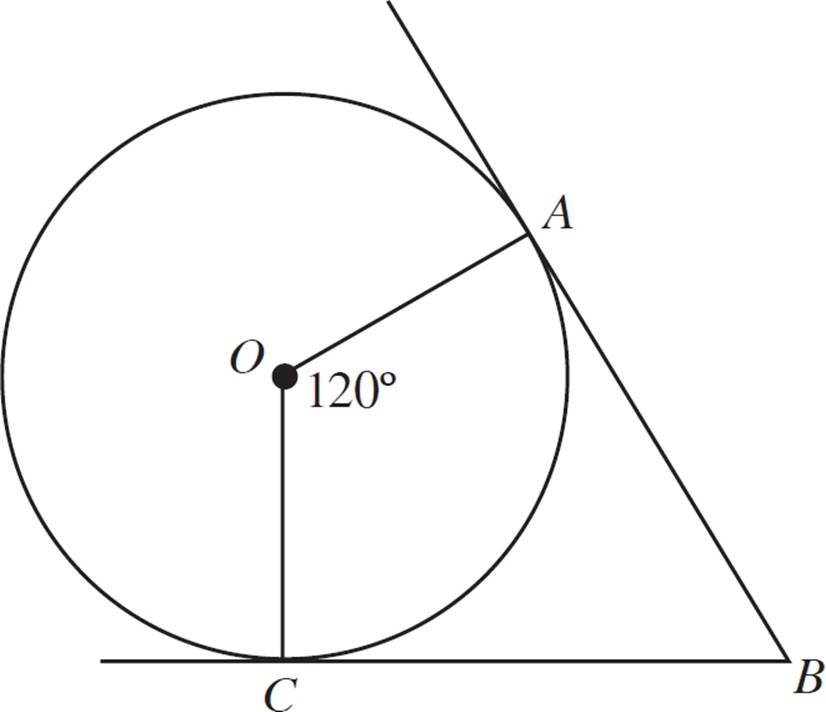
SOLUTIONS TO CHAPTER 7 PRACTICE QUESTIONS
1.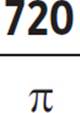
To convert the angle from radians to degrees, use the proportion 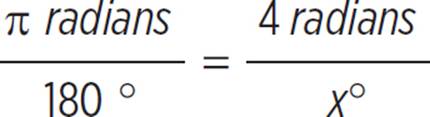 . Cross-multiply to get 720 = πx. Divide both sides by π to get
. Cross-multiply to get 720 = πx. Divide both sides by π to get 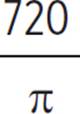 .
.
2.6![]()
The formula for area of a circle is A = πr2. Plug in the area of the circle to get 9 = πr2. Divide both sides by π to get ![]() = r2. Take the square root of both sides to get r =
= r2. Take the square root of both sides to get r = 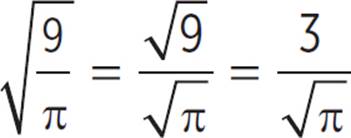 . Plug this into the circumference formula to get C = 2πr = 2π
. Plug this into the circumference formula to get C = 2πr = 2π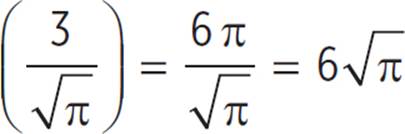 . Reminder: If you have an irrational number in the denominator, you should multiply the fraction by a value of 1 (in this case, multiply
. Reminder: If you have an irrational number in the denominator, you should multiply the fraction by a value of 1 (in this case, multiply 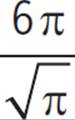 by
by 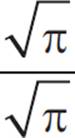 .) This is known as “rationalizing” the denominator.
.) This is known as “rationalizing” the denominator.
3.81π
The question asks for the area of the circle, which is determined by the formula A = πr2. The figure provides an inscribed angle and the length of the intercepted arc. Anytime an arc is mentioned in a geometry question, write the arc formula: 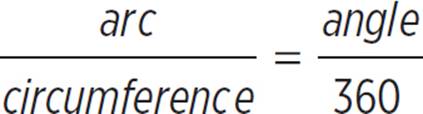 . The measure of the inscribed angle is half the measure of the central angle, so the central angle is 120°. Plug this angle and the arc length into the formula to get
. The measure of the inscribed angle is half the measure of the central angle, so the central angle is 120°. Plug this angle and the arc length into the formula to get 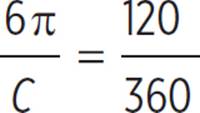 . Reduce the fraction on the right side to get
. Reduce the fraction on the right side to get 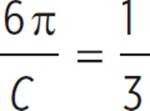 . Cross-multiply to get C = 18π. SinceC = 2πr, 18π = 2πr. Divide both sides by 2π to get r = 9. Plug this into the area formula to get A = πr2 = π(9)2 = 81π.
. Cross-multiply to get C = 18π. SinceC = 2πr, 18π = 2πr. Divide both sides by 2π to get r = 9. Plug this into the area formula to get A = πr2 = π(9)2 = 81π.
4.![]()
The question mentions sector area, so set up a proportion: (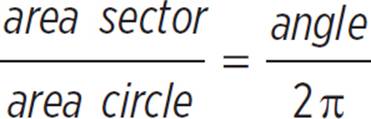 ). Note that we’re using radians here instead of degrees. The area of the sector is 4π. The question asks for the angle, so find the area. The question says that the circumference is 12π. The formula for circumference is C = 2πr, so 12π = 2πr. Divide both sides by 2π to get r = 6. Plug this into the area formula, A = πr2 to get A = π(6)2 = 36π. Plug this into the sector formula to get
). Note that we’re using radians here instead of degrees. The area of the sector is 4π. The question asks for the angle, so find the area. The question says that the circumference is 12π. The formula for circumference is C = 2πr, so 12π = 2πr. Divide both sides by 2π to get r = 6. Plug this into the area formula, A = πr2 to get A = π(6)2 = 36π. Plug this into the sector formula to get 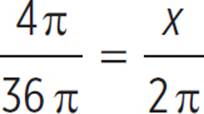 . Reduce the left side of the equation to get
. Reduce the left side of the equation to get 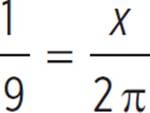 . Cross-multiply to get 9x = 2π. Divide both sides by 9 to get x =
. Cross-multiply to get 9x = 2π. Divide both sides by 9 to get x = ![]() .
.
5.8![]() − 8
− 8
Since the radius is 4, mark off any radius as having a length of 4: OP = OQ = OR = 4. Notice that triangle OPS is a right triangle with a 45° angle. Since there are 180° in a triangle, m∠POS must be 180° − 90° − 45° = 45°, making triangle OPS a 45-45-90 right triangle. The sides of a 45-45-90 right triangle are in a ratio of 1:1:![]() . The side opposite the right angle,
. The side opposite the right angle, ![]() , has a length of 4. To get the length of the other two sides, set up the proportion
, has a length of 4. To get the length of the other two sides, set up the proportion 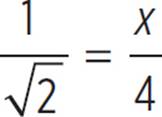 . Cross-multiply to get x
. Cross-multiply to get x ![]() = 4. Divide both sides by
= 4. Divide both sides by ![]() to get x =
to get x =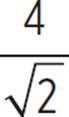 . Rationalize the denominator by multiplying by
. Rationalize the denominator by multiplying by 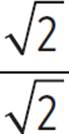 to get x =
to get x = 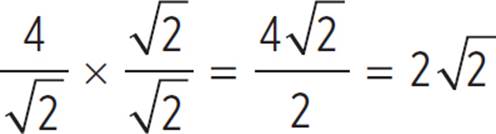 . Therefore, PS = OS = 2
. Therefore, PS = OS = 2![]() . Since
. Since ![]() is a radius that is perpendicular to chord
is a radius that is perpendicular to chord ![]() ,
, ![]() bisects
bisects ![]() , so PS = SR = 2
, so PS = SR = 2![]() . Chord
. Chord ![]() is the base of triangle PQR. The height is
is the base of triangle PQR. The height is ![]() . To get QS, subtract OS from OQ to get QS = 4 − 2
. To get QS, subtract OS from OQ to get QS = 4 − 2![]() . Plug these into the area formula to get A =
. Plug these into the area formula to get A = ![]() bh =
bh = ![]() (4
(4![]() )(4 − 2
)(4 − 2![]() ) = (2
) = (2![]() )(4 − 2
)(4 − 2![]() ) = 8
) = 8![]() − (2
− (2![]() )2 = 8
)2 = 8![]() − 8.
− 8.
6.100π
The radii of the two circles have a radius of 5:3, so let their values equal 5x and 3x, respectively. The area of the annulus is the difference between the areas of the two circles. Since the radius of the larger circle is 5x, the area is A = πr2 = π(5x)2 = 25πx2. Since the radius of the smaller circle is 3x, the area is A = πr2 = π(3x)2 = 9πx2. The area of the annulus is the difference between these two, which is 25πx2 − 9πx2 = 16πx2. The question says that this is 64π, so 64π = 16πx2. Divide both sides by 16π to get 4 = x2. Take the square root of both sides to get x = 2. The question asks for the area of the larger circle. Since x = 2, the radius is 5x = 5(2) = 10. The area is A = πr2 = π(10)2 = 100π. Alternatively, plug x = 2 into the previous derived expression for the area of the larger circle, 25πx2, to get 25π(2)2 = 25π(4) = 100π.
7.6π
The shaded region is the difference between the two sectors. Determine the area of each sector and find the difference. Start with the larger circle, which has a circumference of 16π. Sector area directly relates to circle area rather than circumference, so use the circumference to get the area. The circumference formula is C = 2πr, so 16π = 2πr. Divide both sides by 2π to get r = 8. Plug this into the area formula to get A = πr2 = π(8)2 = 64π. Plug this into the radians version of the sector formula, 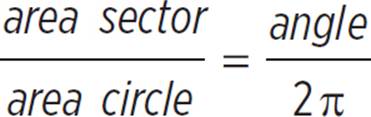 , to get
, to get 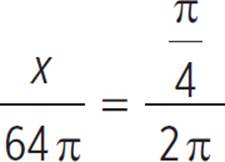 . Cross-multiply to get 16π2 = 2πx. Divide both sides by 2π to get x = 8π. Follow a similar method to get the area of the smaller arc. Since the circumference is 8π, 8π = 2πr, and r = 4. Therefore, A = πr2 = π(4)2 = 16π. Plug this into the sector formula to get
. Cross-multiply to get 16π2 = 2πx. Divide both sides by 2π to get x = 8π. Follow a similar method to get the area of the smaller arc. Since the circumference is 8π, 8π = 2πr, and r = 4. Therefore, A = πr2 = π(4)2 = 16π. Plug this into the sector formula to get 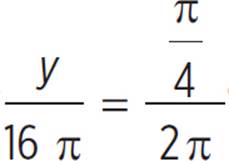 . Cross-multiply to get 4π2 = 2πy. Divide both sides by 2π to get y = 2π. Subtract the two sectors to get 8π − 2π = 6π.
. Cross-multiply to get 4π2 = 2πy. Divide both sides by 2π to get y = 2π. Subtract the two sectors to get 8π − 2π = 6π.
8. ![]()
There’s no formula for the area of a quadrilateral that isn’t a parallelogram or a trapezoid, so break this into figures that have a formula: in this case, two triangles. Since CB and AB are tangent to the circle, they form right angles with the radius. Since right angles tend to make geometry easier, don’t break up the right angles. Instead, draw the segment OB to form the two triangles. Since segments AB and CB are tangent to the circle, we know that segment OB bisects ∠ABC, so m∠BOC = m∠AOB = 60°. Look at one triangle at a time. Start with triangle BOC. Since ∠OCB is a right angle and m∠BOC = 60°, m∠OBC = 30°, making the triangle a 30-60-90. The sides in a 30-60-90 triangle are in a ratio of 1:![]() :2. Since radius OC is opposite the 30° and has a length of 1 (given), side BC, which is opposite the 60° angle, has a length of
:2. Since radius OC is opposite the 30° and has a length of 1 (given), side BC, which is opposite the 60° angle, has a length of ![]() , and OB, which is opposite the 90° angle, has a length of 2. Use CB as the base and OC as the height, and plug these values into the area formula to get A =
, and OB, which is opposite the 90° angle, has a length of 2. Use CB as the base and OC as the height, and plug these values into the area formula to get A = ![]() bh =
bh = ![]() (
(![]() )(1) =
)(1) = 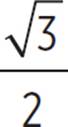 . Now look at triangle AOB. Follow a similar line of reasoning to determine that this is also a 30-60-90 triangle with sides 1,
. Now look at triangle AOB. Follow a similar line of reasoning to determine that this is also a 30-60-90 triangle with sides 1, ![]() , and 2. (Alternatively, prove that the triangles are congruent using AAS or ASA.) Since the triangles are congruent, double the area of the first triangle to get the total area:
, and 2. (Alternatively, prove that the triangles are congruent using AAS or ASA.) Since the triangles are congruent, double the area of the first triangle to get the total area: 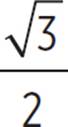 × 2 =
× 2 = ![]() .
.
REFLECT
Congratulations on completing Chapter 7!
Here’s what we just covered.
Rate your confidence in your ability to:
•Understand tangent lines, secant lines, and chords, and the relationships among these and other parts of a circle
![]()
•Calculate the length of an arc, or the area of a sector of a circle
![]()
•Solve problems using the ratios of arc length : circumference, sector area : total area, and central angle : total angle
![]()
•Understand the relationships between inscribed and central angles
![]()
•Solve problems with concentric circles
![]()
•Understand radians, and convert between radians and degrees
![]()
If you rated any of these topics lower than you’d like, consider reviewing the corresponding lesson before moving on, especially if you found yourself unable to correctly answer one of the related end-of-chapter questions.

Access your online student tools for a handy, printable list of Key Points for this chapter. These can be helpful for retaining what you’ve learned as you continue to explore these topics.
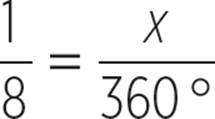
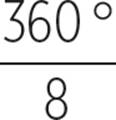 = x
= x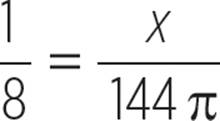
 = x
= x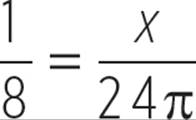
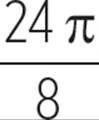 = x
= x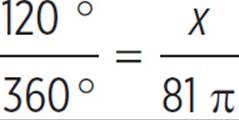
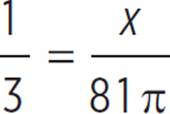
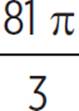 = x
= x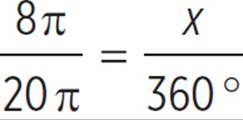
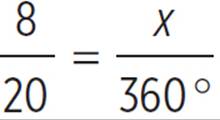
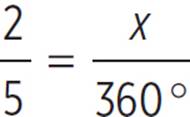
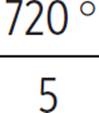 = x
= x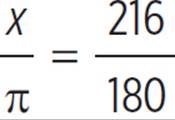
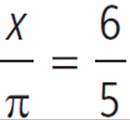
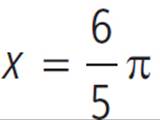
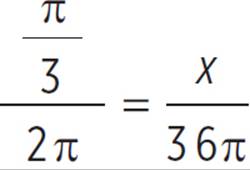
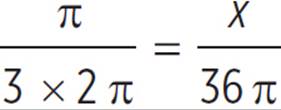
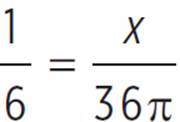
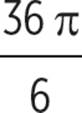 = x
= x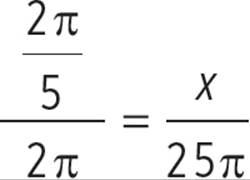
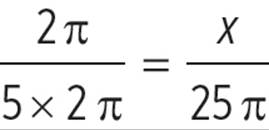
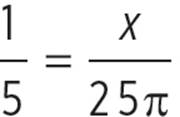
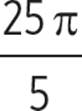 = x
= x