High School Geometry Unlocked (2016)

Lesson 1.4. Rotation

In everyday language, “rotation” means turning or spinning around, such as with a wheel. In geometry, rotation means turning a figure around a fixed point. That point is called the center of rotation.

You may need to draw a rotation of a figure, identify the angle of rotation, or write an algebraic expression for a rotation.

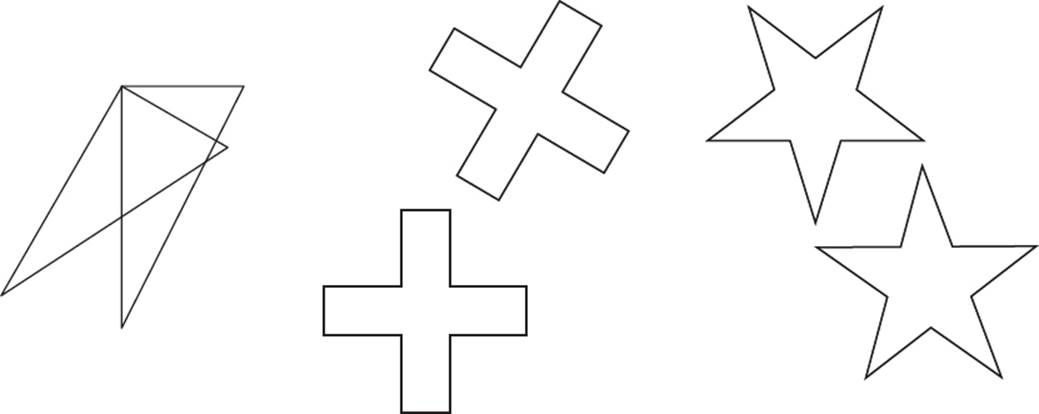
Examples of Rotations

You can imagine a rotation as a pair of hands on a clock. The center of the clock, where both hands are attached, is like the center of rotation. The numbers that the hands point to are analogous to the image and pre-image points of a figure.

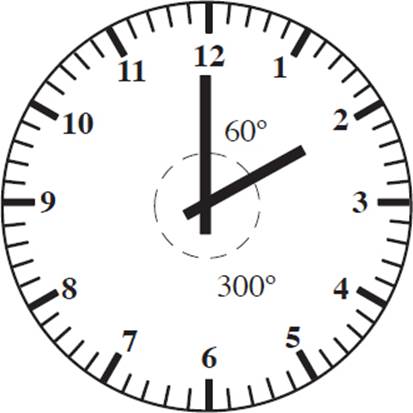
The figure above illustrates that there is a 60° angle between the 12 and 2. In fact, you can measure the angle from two different directions: clockwise or counterclockwise. (In the example above, the angle measured counterclockwise would be 60°, and the same angle measured clockwise would be −300°.) Both measurements are valid; however, it’s important to remember the difference in signs.

Rotations are positive when measured in the counterclockwise direction.

Rotations are negative when measured in the clockwise direction.

When you’re given a corresponding image and pre-image point, you can measure the angle of rotation by drawing the angle between them. More specifically, draw a line segment from the image point to the center of rotation, then another segment from the pre-image point to the center of rotation. The two line segments form an angle, which you can then measure with a protractor.

“Clockwise” is the
direction of the hands
of a clock (i.e. as the
hands move from 1
to 2 to 3, and so on).
“Counterclockwise” is
the opposite direction.

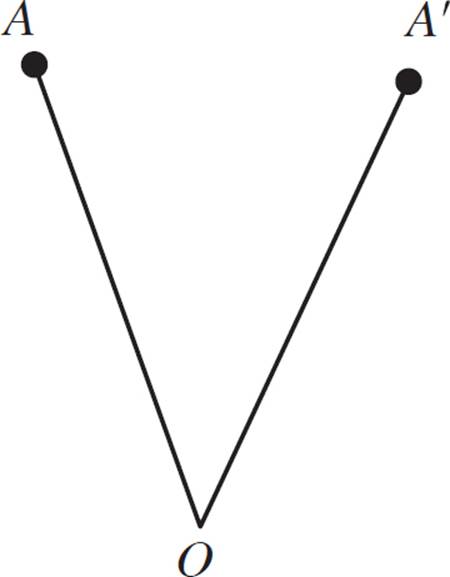
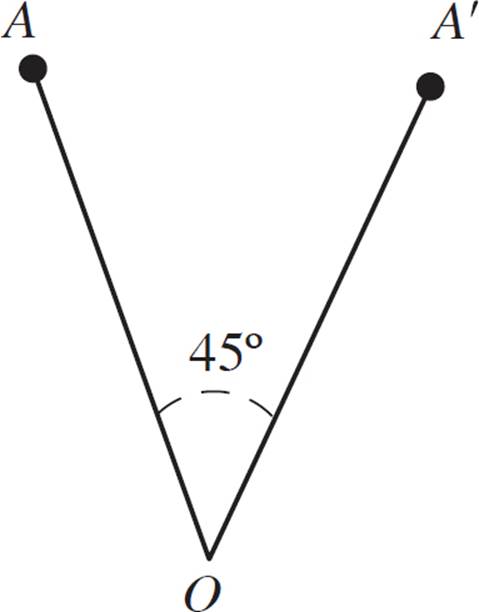
In the figure above, point A′ is the image of A, and point O is the center of rotation. Identify the angle of rotation for point A about point O.

Here, you’re asked to identify the angle of rotation. First, draw a line from point O through point A, and another line from point O through point A′. Use a protractor to measure the angle between these two segments.

Supplies

Remember, you can
download larger
versions of the images
in the Example
problems from your
student tools online.

Your measurement should be very close to 45°. (See the illustration below).

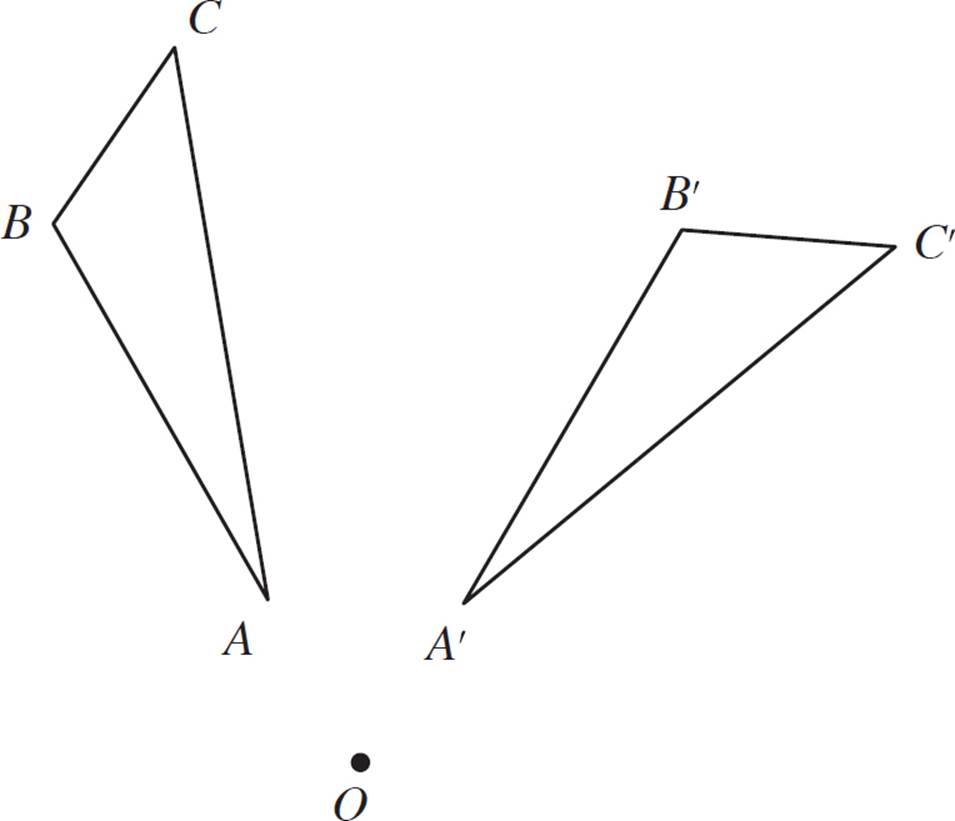
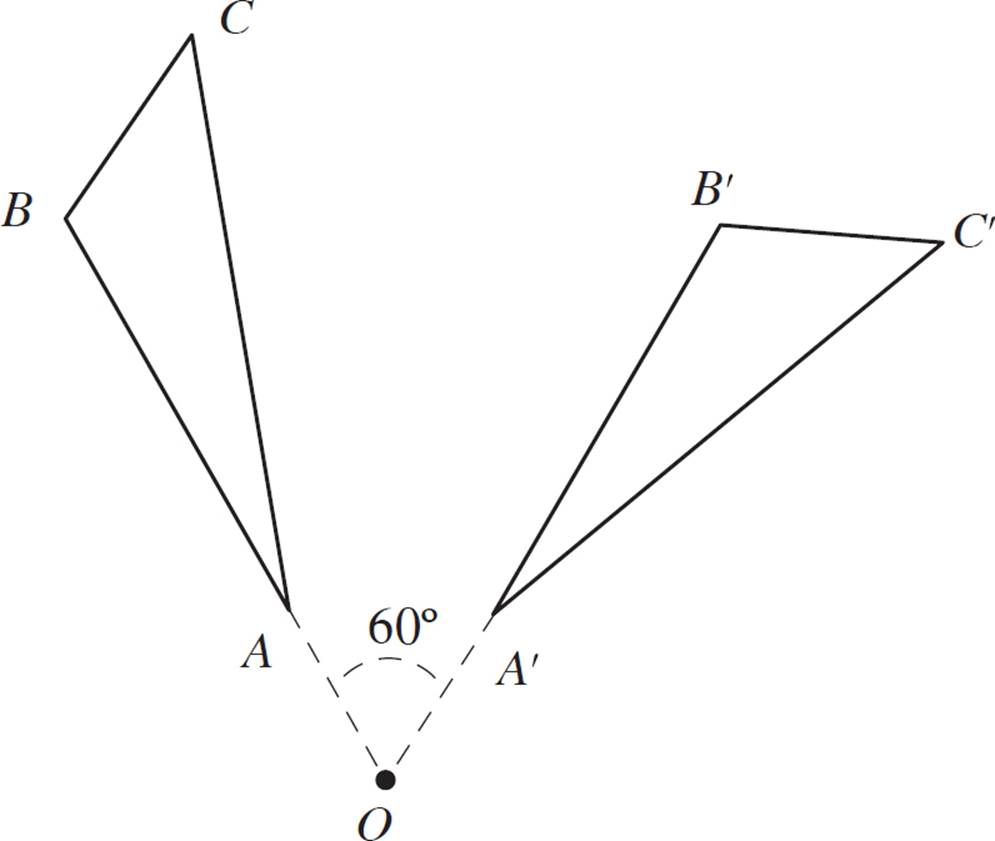
In the figure above, triangle A′B′C′ is the image of triangle ABC, and point O is the center of rotation. Identify the angle of rotation for triangle ABC about point O.

In this example, you’re asked to identify the angle of rotation for a triangle. You can do this the same way that you dealt with the single point in Example 11, and in fact, you have to use only one point from the triangle, along with its corresponding image point.

First, choose a point to work with. How about A? Draw a line segment from point O through point A. Then, draw another line segment from point O through point A′. Use a protractor to measure the angle between the two segments.

Your measurement should be very close to 60°. (See the illustration below).

Here is how you may see triangle rotation on the ACT.

Isosceles triangle DEF is shown in the standard (x, y) coordinate plane below. The coordinates for two of its vertices are D (0, 0) and E (c, d).

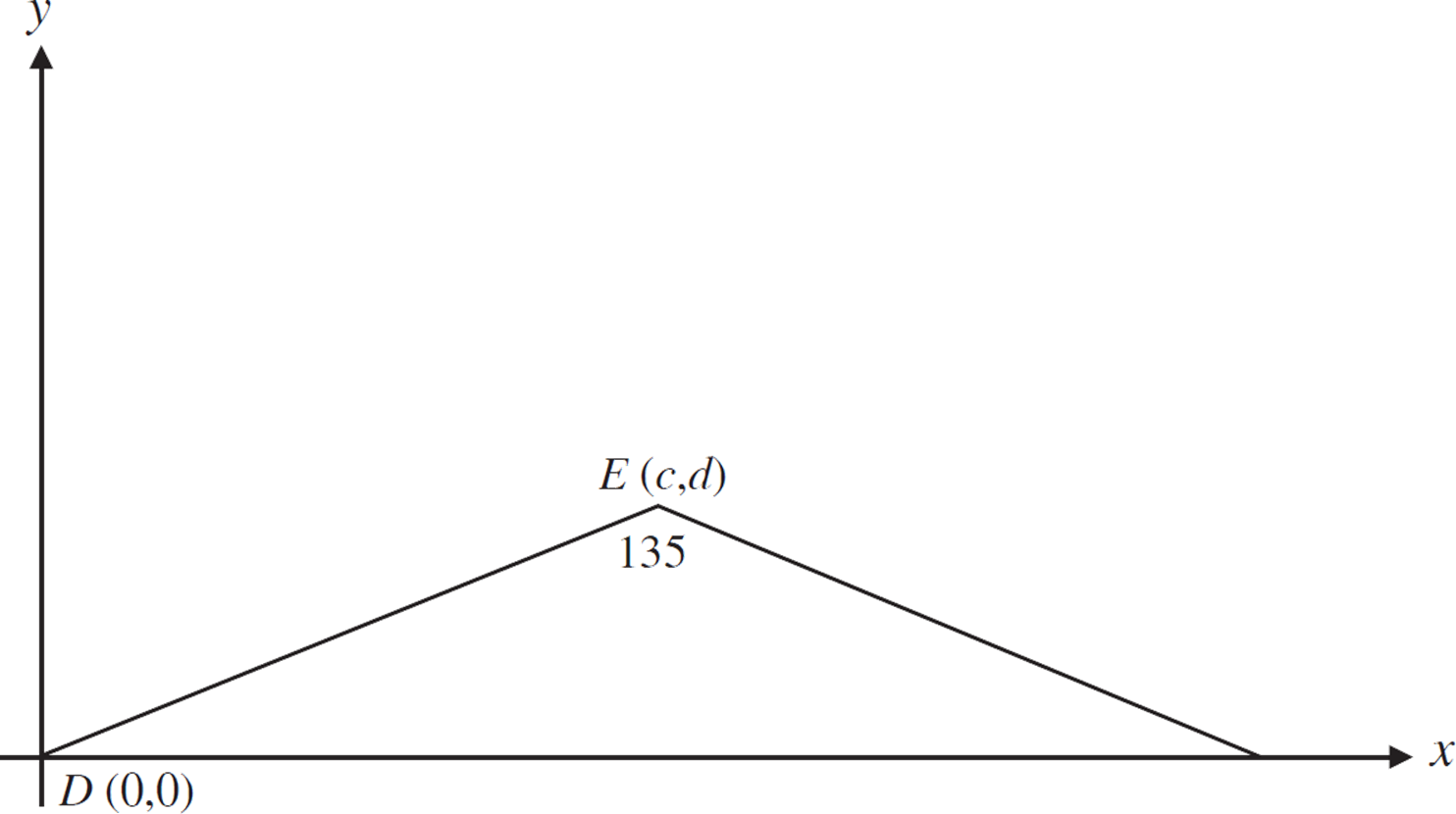
Isosceles triangle DEF is rotated clockwise by 180° about the origin. At what ordered pair is the image of E located?

A.(−c, d)

B.(c, −d)

C.(−d, −c)

D.(−c, −d)

E.(d, c)

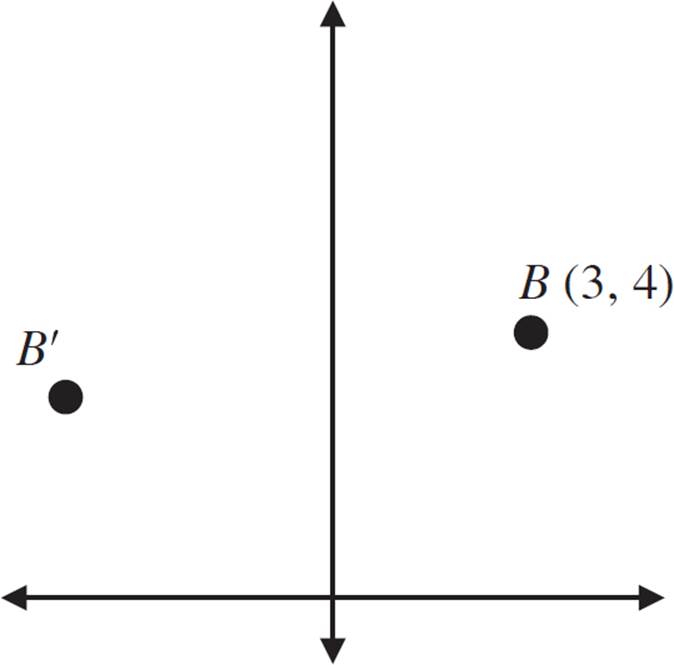
In the figure above, point B has been rotated 90° about the origin, resulting in point B′. What are the coordinates of point B′?

When dealing with rotations of 90°, one way to approach it is by using rectangles. If you draw a rectangle connecting point B to the y-axis and the x-axis, as shown below, you can draw the image rectangle by turning it over on its side. The horizontal length of the pre-image becomes the vertical length of the image, and vice versa. In other words, the pre-image rectangle has a horizontal length of 3 units and a vertical length of 4 units; therefore, the image rectangle has a horizontal length of 4 units and a vertical length of 3 units.

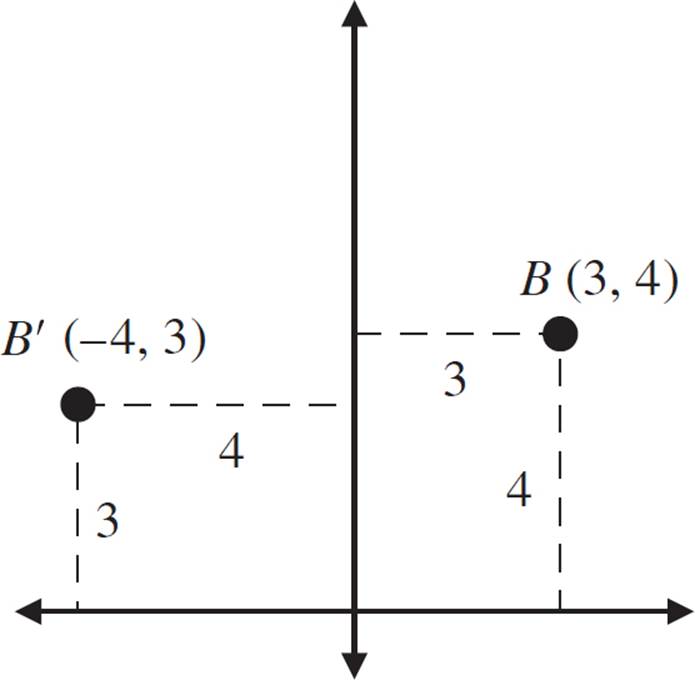
When rotating figures, remember that if you change to a different quadrant in the coordinate plane, you’re going to change the sign of one or both coordinates. Check where you are on the axes. In this case, the x-coordinate is negative.

Notice how this rotation affected the coordinates: The pre-image coordinate is (3, 4) and the image coordinate is (−4, 3). We’ll go over the algebraic rule for this in just a bit.

First, let’s see one more example using the rectangle approach.

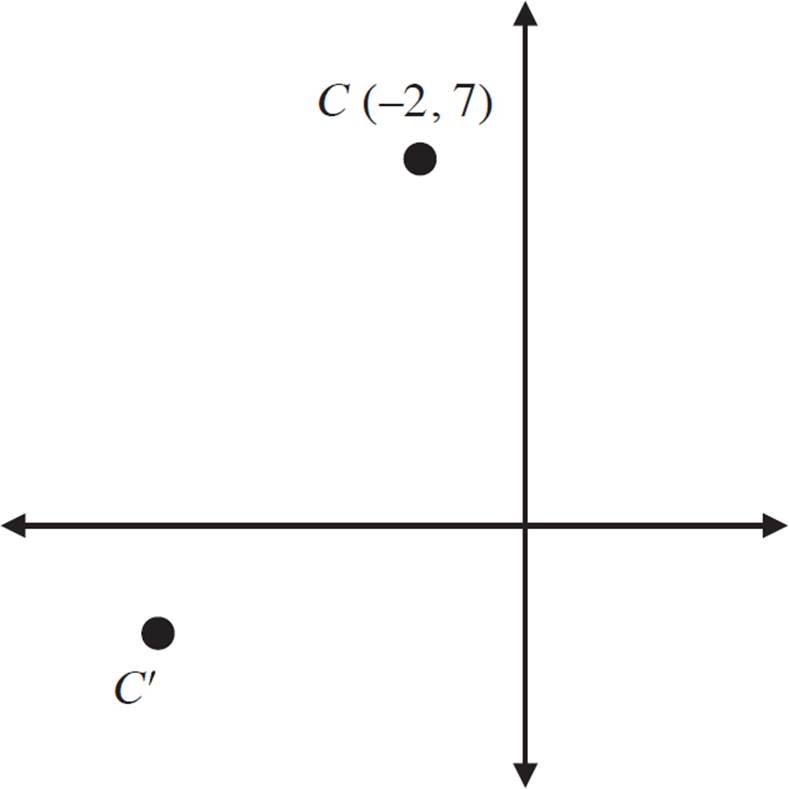
In the figure above, point C has been rotated 90° about the origin, resulting in point C′. What are the coordinates of point C′?

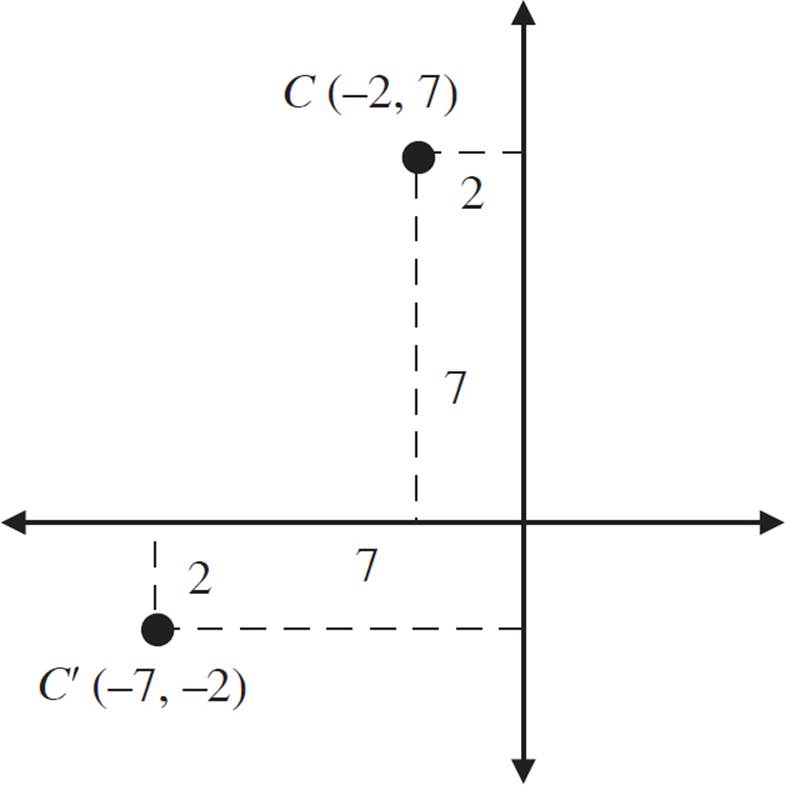
In this example, point C has a negative coordinate, but you can approach it the same way as in the previous example. Draw a rectangle connecting point C to the y-axis and x-axis. This rectangle has a horizontal length of 2 and a vertical length of 7. Turn the rectangle on its side (remember to go counterclockwise); it will have a horizontal length of 7 and a vertical length of 2. In this quadrant, both the x-coordinate and the y-coordinate are negative. The coordinate of C′ is (−7, −2).

When the triangle is rotated 180°, point E will lie in quadrant III. In quadrant III, both coordinates will be negative, which means (A), (B), and (E) can be eliminated. Point E will be the same distance from the origin on both the x- and y-axes, but in the opposite direction, so both coordinates should be the opposite of the original values, or (−c, −d), as in (D).

You can use the same approach for rotations of 180°, 270°, or 360°, since these angles are multiples of 90°. 180° is two turns of 90°:

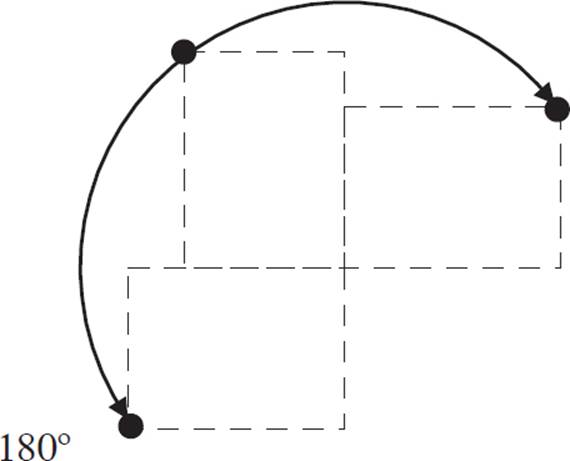
270° is three turns of 90°:

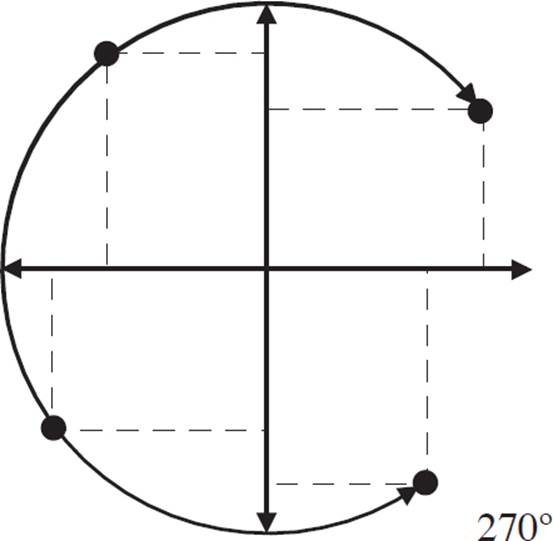
360° is four turns of 90°:

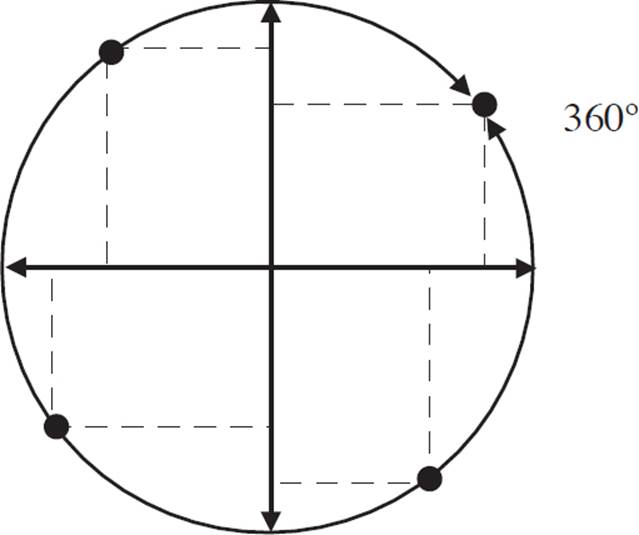
For rotations of 90° and multiples of 90°, use the following rules (note that these rules work only when the center of rotation is the origin):

Rotation Rules for Points

If the center of rotation is the origin (0, 0), then:

R_90° (x, y) = (−y, x)

R_180° (x, y) = (−x, −y)

R_270° (x, y) = (y, −x)

R_360° (x, y) = (x, y)