High School Geometry Unlocked (2016)

Lesson 1.5. Symmetry

A figure has symmetry if, after certain transformations, the image is identical to the pre-image, and in the same position. There are different kinds of symmetry, including reflectional symmetry and rotational symmetry. Some figures have no symmetry, some have exactly one kind of symmetry, while others may have multiple kinds of symmetry.

REFLECTIONAL SYMMETRY

A figure has reflectional symmetry when one half of the image is the mirror image of the other half. In other words, the reflected image just overlaps itself. This is also known as line symmetry or mirror symmetry. When people talk about “symmetry” in everyday language, they’re most likely referring to reflectional symmetry.

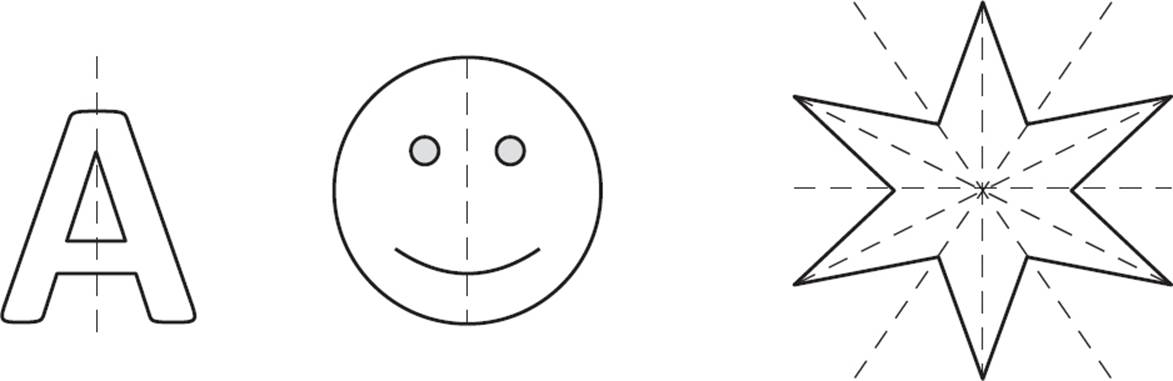
Examples of Figures with Reflectional Symmetry

A line of symmetry is the line of reflection that results in symmetry.

Think of a line of symmetry as a fold line in a piece of paper. If you can fold a shape and have two identical halves that line up with each other, the shape has line symmetry. A figure can have no lines of symmetry, one line of symmetry, or multiple lines of symmetry.

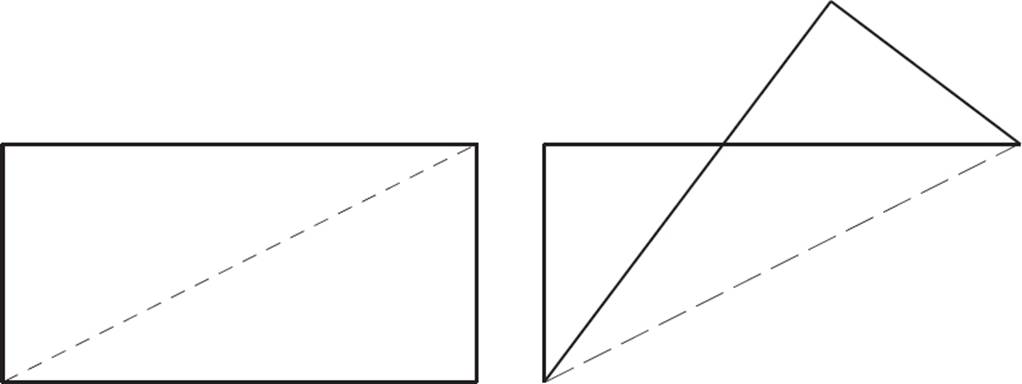
A rectangle has two lines of symmetry. If you fold it in half vertically or horizontally, you produce two identical halves that line up with each other.

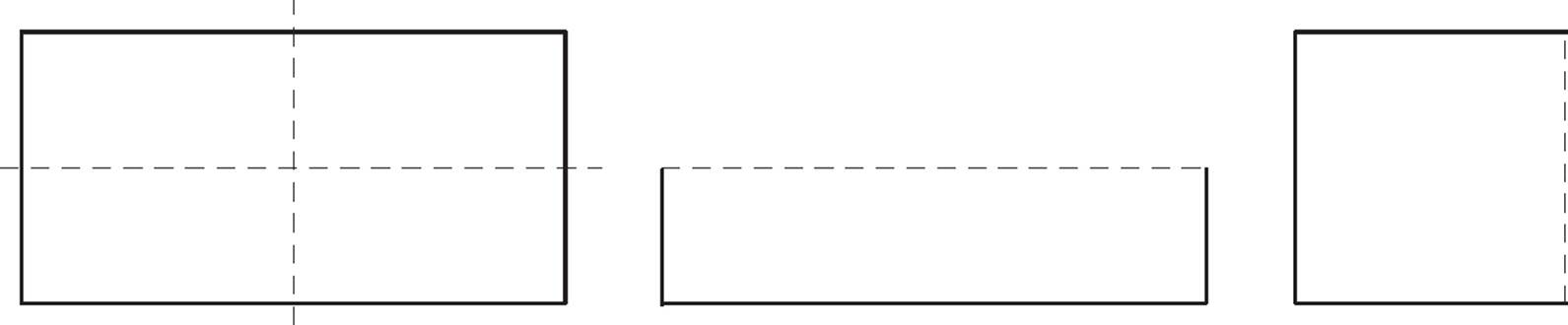
However, if you fold the rectangle in half diagonally, the two halves do not match up, even though they are congruent. This is NOT a line of symmetry.

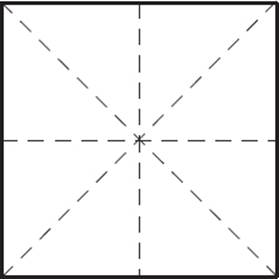
A square has 4 lines of symmetry.

Here is how you may see symmetry on the ACT.

Which of the following geometric figures has at least 1 rotational symmetry and at least 1 reflectional symmetry?

(Note: The angle of rotation for the rotational symmetry must be less than 360°.)

A.

B.

C.

D.

E.

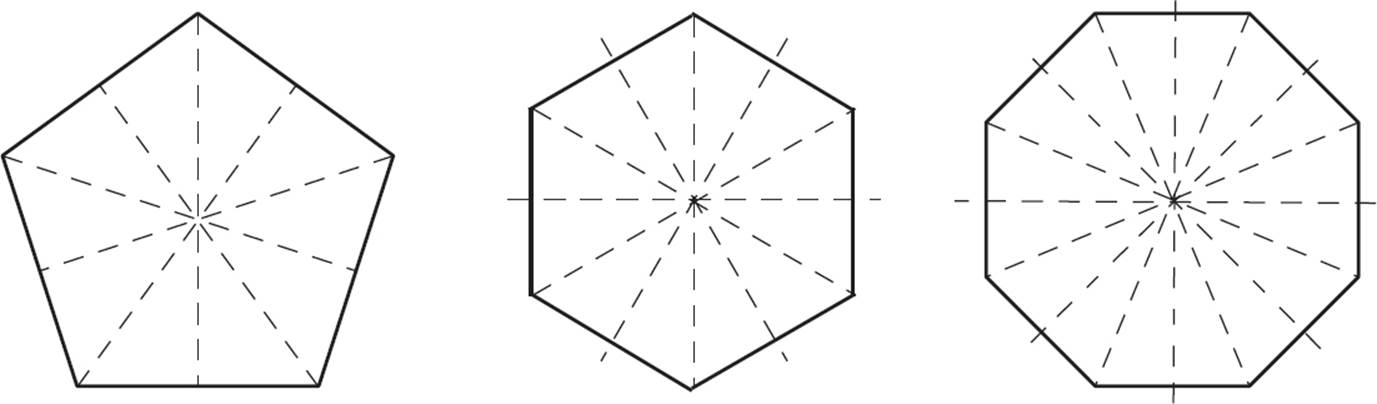
Additionally, any regular polygon has the same number of symmetry lines as it does sides. A regular pentagon has 5 lines of symmetry, a regular hexagon has 6 lines of symmetry, and so on.

To see how parabola
symmetry is tested on
the SAT, access your
Student Tools online.

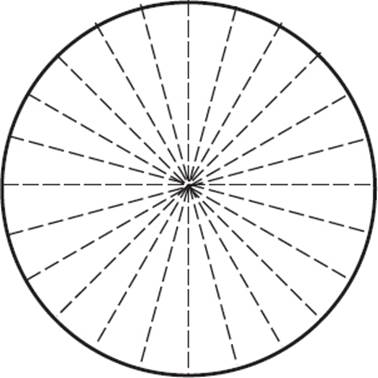
A circle has infinite lines of symmetry!

ROTATIONAL SYMMETRY

A figure has rotational symmetry if a rotation (other than 0° or 360°) produces the same image overlapping itself.

Examples of Figures with Rotational Symmetry

The order of rotational symmetry for a figure is the number of rotations for which the figure has symmetry.

For example, if a figure has order 2 rotational symmetry, then it looks the same at 180° and 360° rotations.

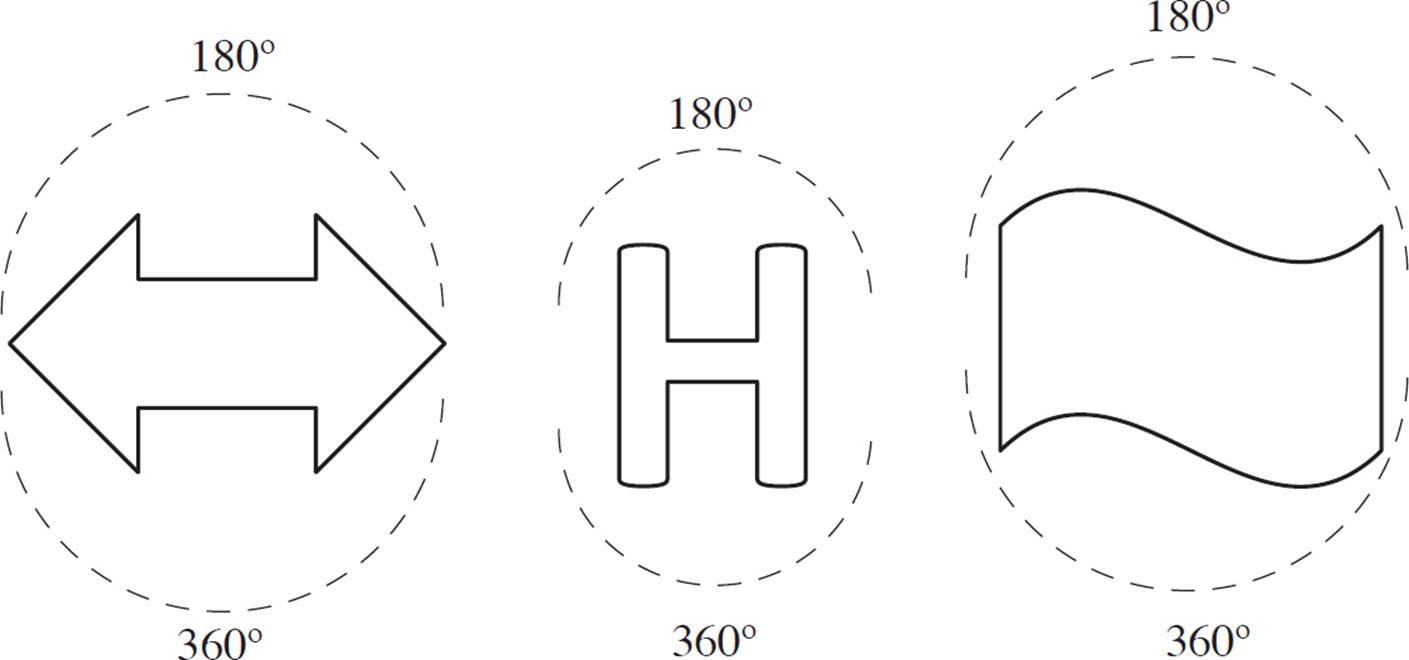
Examples of Figures with Order 2 Rotational Symmetry

There’s really no such thing as “order 1” symmetry—that would just mean that something looks the same when you turn it completely around, and that’s true for every figure.

If a figure has order 3 rotational symmetry, then it looks the same at 120°, 240°, and 360°.

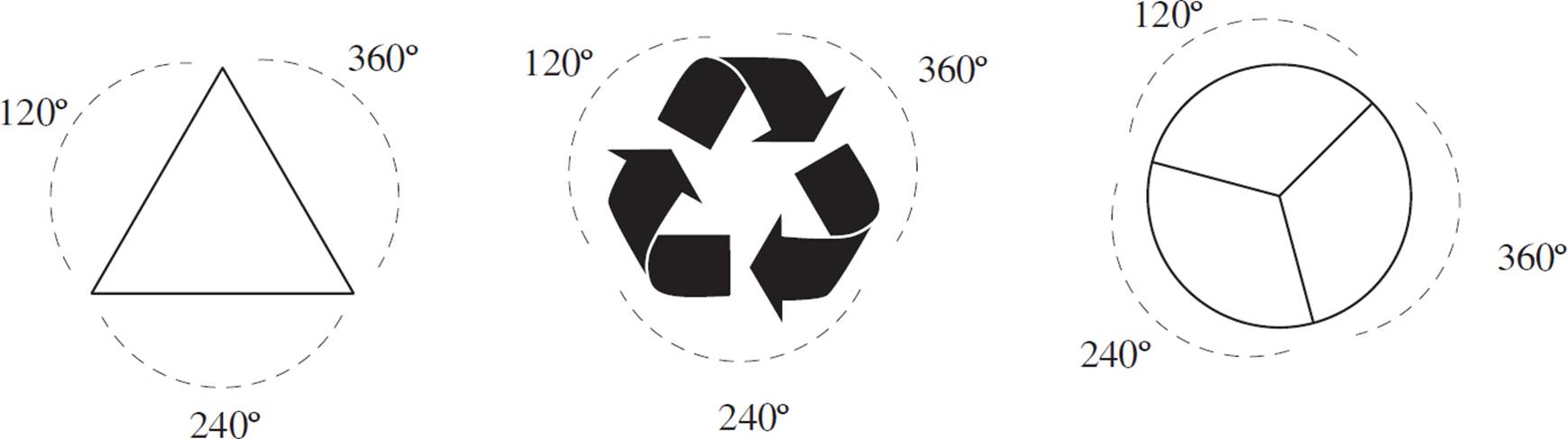
Examples of Figures with Order 3 Rotational Symmetry

A geometric figure has rotational symmetry if it looks the same after a certain amount of rotation. A geometric figure has reflectional symmetry when one half is the reflection of the other half. Choice (C) is the only figure that has rotational and reflectional symmetry.

And so on. The order of symmetry always divides the full rotation evenly.

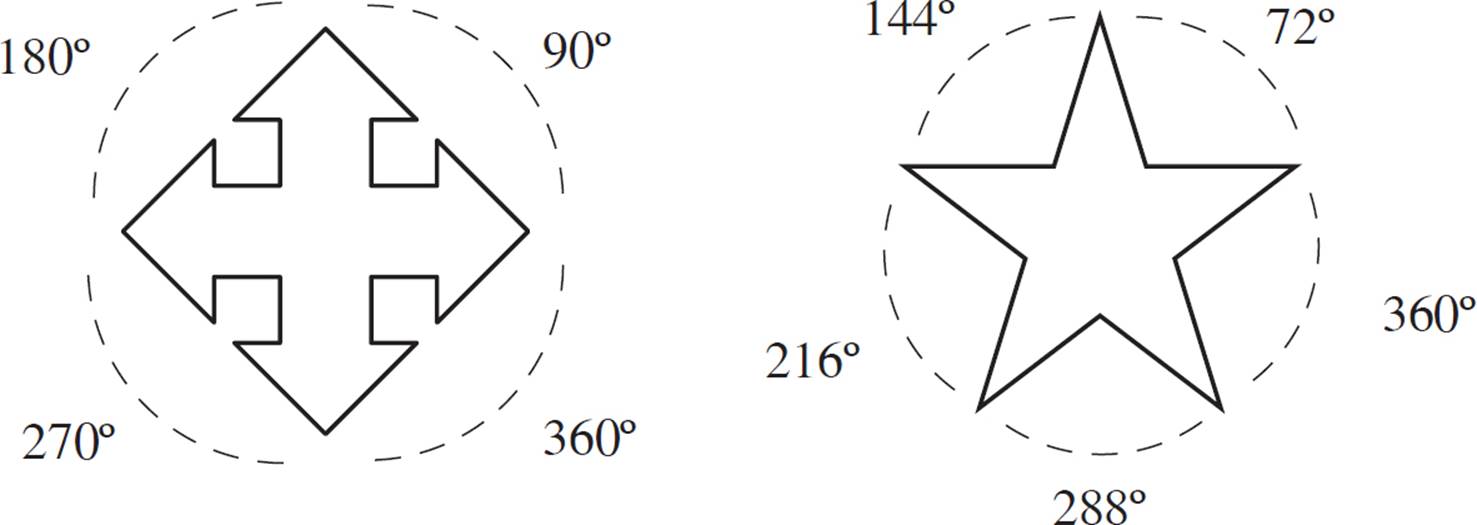
Any regular polygon has the same order of symmetry as the number of its sides. For example, a regular pentagon has order 5 symmetry, a regular hexagon has order 6 symmetry, and so on.

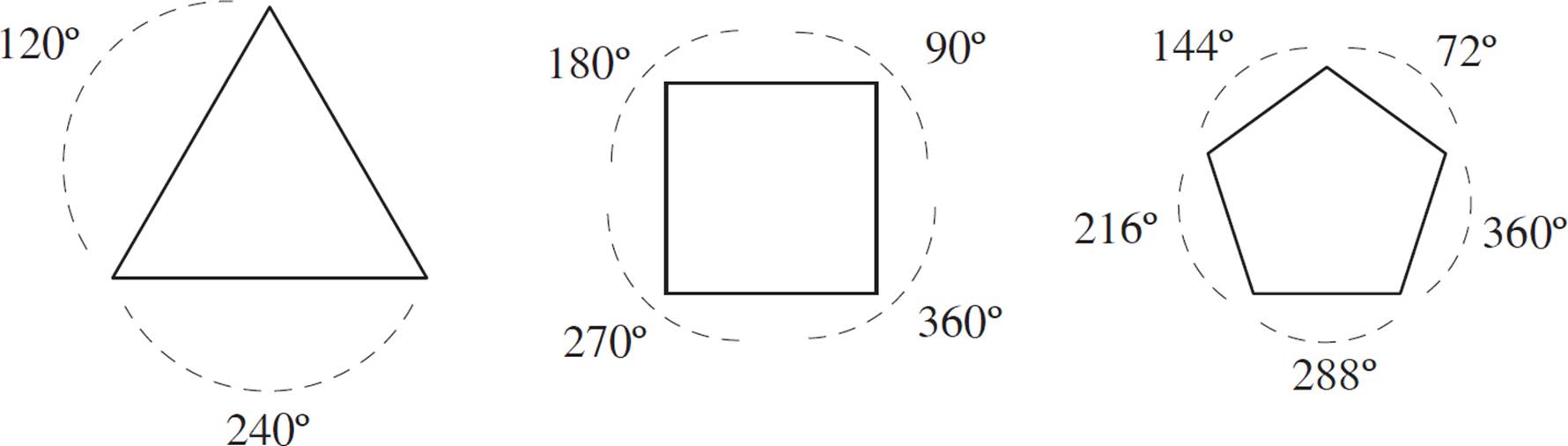
A circle has infinite rotational symmetry!

DRILL

CHAPTER 1 PRACTICE QUESTIONS

Directions: Complete the following problems as specified by each question. For extra practice after answering each question, try using an alternative method to solve the problem or check your work. Larger, printable versions of images are available in your online student tools.

Click here to download a PDF of Chapter 1 Practice Questions.

1.ABCD is a quadrilateral with coordinates A (−5, 2), B (6, 1), C (1, −5), and D (−2, −3). Find the vertices of A′B′C′D′ under the translation (x + 3, y − 6).

2.Given D (1, 3), E (4, 7), D′ (4, −2), and E′ (7, 2), determine whether DE and D′E′ are parallel.

3.For each of the coordinates given below, find the new ordered pair by:

1. Reflecting along the x-axis

2. Reflecting along the y-axis

3. Reflecting along the line y = x

a.(5, 5)

b.(2, −7)

c.(−3, 0)

d.(−4, −2)

4.For each of the following questions, check all that apply.

a.Which of the following types of transformations result in congruent figures?

□Moving a figure (up, down, left, right, or diagonally)

□Flipping a figure across a line

□Rotating a figure about a point

□Changing the size of a figure

b.Which of the following types of transformations are called rigid motions?

□Moving a figure (up, down, left, right, or diagonally)

□Flipping a figure across a line

□Rotating a figure about a point

□Changing the size of a figure

5.The figure below is the graph of f(x) = .

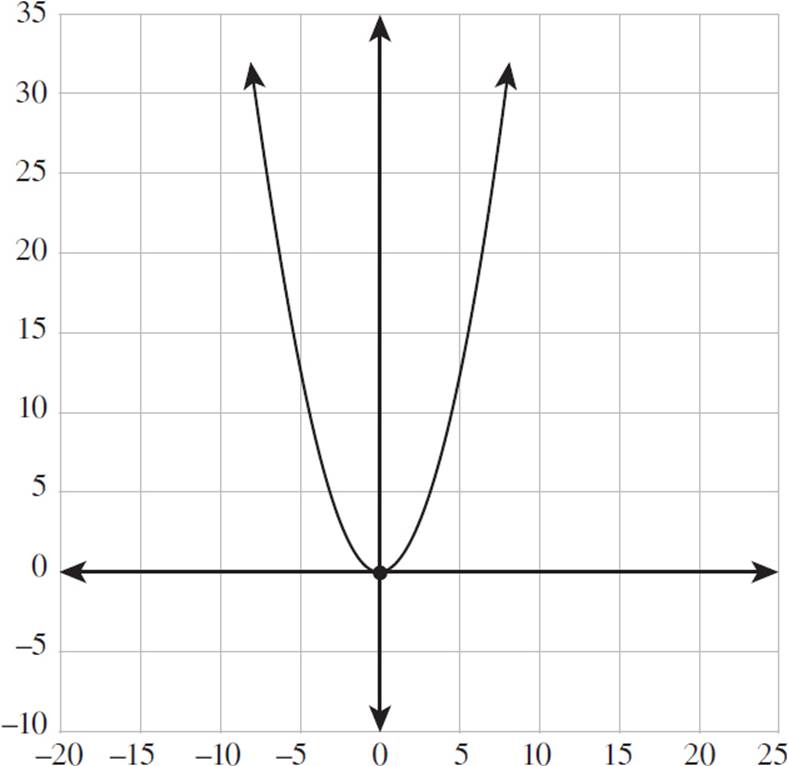
Sketch the graph of f(x) − 5.

6.

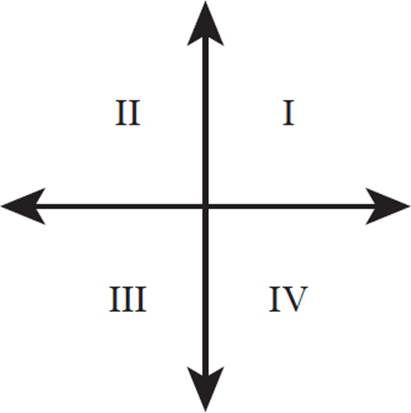
For each of the following, determine which quadrant (I, II, III, or IV) the resulting figure will be in after applying the given reflection:

a.A circle centered at (−4, 3) with a radius of 1 reflected across the line x = 0

b.A quadrilateral with vertices (−3, −2), (−3, −5), (−7, −5), and (−3, −5) reflected across the line y = x

c.A triangle with vertices located in quadrant IV reflected across the line y = 1

d.A square with vertices (1, 1), (1, 5), (5, 1), and (5, 5) reflected across the line y = x

7.Which letters of the alphabet (as written in the style below) have a rotational symmetry of 180°?

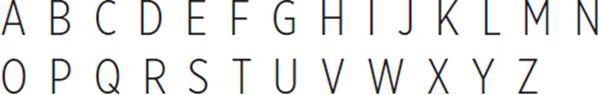
8.The graph below shows a quadrilateral with vertices (5, −5), (10, 10), (15, 10), and (15, 5).

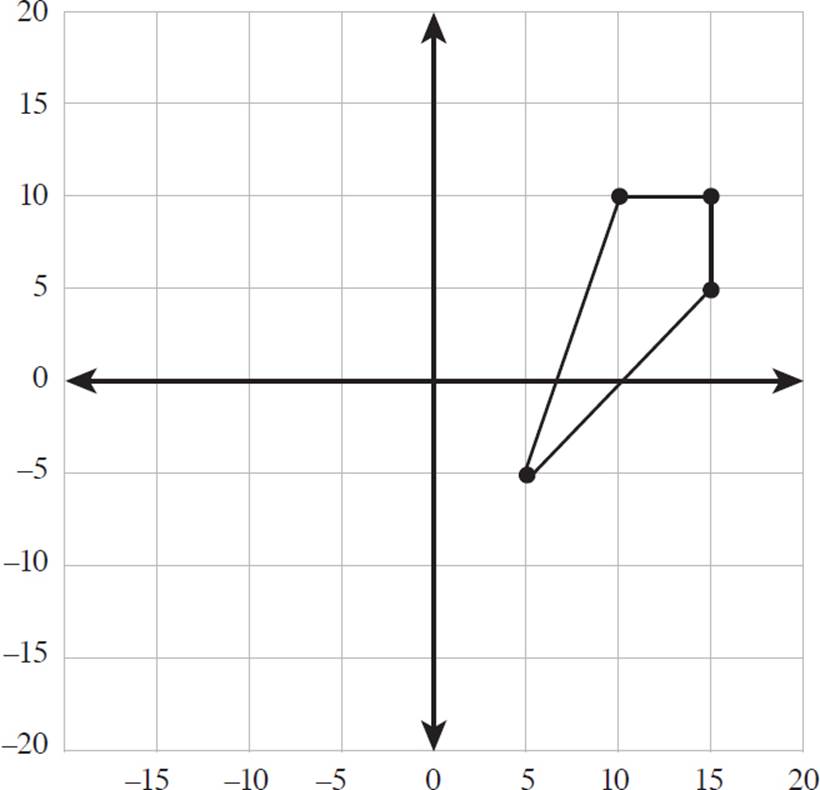
Sketch the rotation of the quadrilateral 270° about the origin.

9.Two dancers are performing a routine, during which they will always maintain precisely 3 feet of space between them. The stage is 30 ft by 20 ft, and the starting position for Dancer A is 10 ft right and 5 ft up, with respect to the bottom left corner (as shown in the figure).

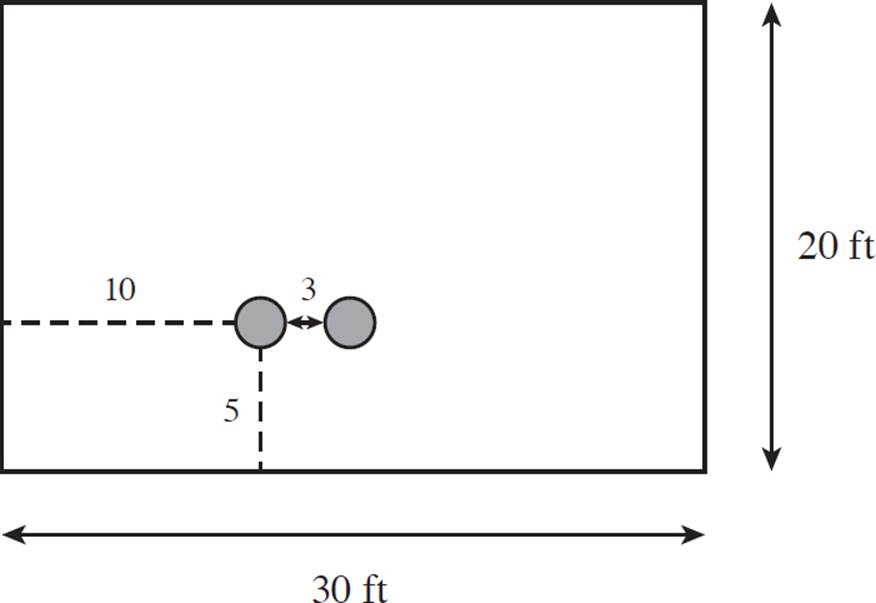
If the final position of the dancers is represented by a 90° rotation about Dancer A, and a translation of (10, 5) (horizontal and vertical, respectively), what is the final position of the dancers? Sketch your response in the figure (draw the approximate location, and label distances).

Note: All units are in feet.

10. In the figure below, a person has taken a photo of herself while facing a mirror. The image begins to circulate on the Internet, with people debating whether the subject of the photo is holding the phone in her left or right hand.

Who is correct here? Is the subject holding her phone in her left or right hand?

SOLUTIONS TO CHAPTER 1 PRACTICE QUESTIONS

1.The coordinates are A′(−2, −4), B′ (9, −5), C′ (4, −11), and D′ (1, −9).

For each coordinate, find A′ by adding 3 to each x-coordinate and subtracting 6 from each y coordinate

2.The segments are parallel.

One way to determine whether the segments are parallel is to check the translations of the given coordinates for consistency. That is, see if both pairs of coordinates are translated the same way. Another option, if you know how the slopes of parallel lines are related, is to compare the slopes of the two segments. (You’ll learn more about this in Chapter 6). Here’s how to compare the translations of the two coordinates:

D (1, 3) and D′ (4, −2): 4 − 1 is a shift of 3 units to the right and −2 − 3 is a shift of −5 units (pay attention to the negative!). This means a shift of 5 units down.

E (4, 7) and E′ (7, 2): 7 − 4 is a shift of 3 units to the right and 2 − 7 is a shift of −5 units (pay attention to the negative!). This means a shift of 5 units down.

Since D′E′ is created by applying the same shift to each endpoint of DE, the two lines are parallel to each other.

3.Recall the following rules:

1. To reflect a coordinate across the x-axis, change the sign of the y-coordinate.

This is what you should do for step 1 for each coordinate.

2. To reflect a coordinate across the y-axis, change the sign of the x-coordinate.

This is what you should do for step 2 for each coordinate.

3. To reflect a coordinate across the line y = x, switch the x- and y-coordinates.

This is what you should do for step 3 for each coordinate.

a.Given (5, 5)

1. (5, −5)

2. (−5, 5)

3. (5, 5)

Change the sign of the y-coordinate.

Change the sign of the x-coordinate.

Switch the x- and y-coordinates. Since the coordinate already lies on the line y = x, the reflected coordinate is the same.

b.Given (2, −7)

1. (2, 7)

2. (−2, −7)

3. (−7, 2)

Change the sign of the y-coordinate.

Change the sign of the x-coordinate.

Switch the x and y coordinates.

c.Given (−3, 0)

1. (−3, 0)

2. (3, 0)

3. (0, −3)

Change the sign of the y-coordinate. Since the coordinate is on the x-axis, the reflected coordinate is the same.

Change the sign of the x-coordinate.

Switch the x- and y-coordinates.

d.Given (−4, −2)

1. (−4, 2)

2. (4, −2)

3. (−2, −4)

Change the sign of the y-coordinate.

Change the sign of the x-coordinate.

Switch the x- and y-coordinates.

4.The answers to both (a) and (b) are the same:

✓ Moving a figure (up, down, left, right, or diagonally)

✓ Flipping a figure across a line

✓ Rotating a figure about a point

If you move, flip, or rotate a figure, the original and resulting figures are congruent. These types of transformations (also known respectively as translations, reflections, and rotations) are called rigid motions.

Congruent figures have the same shape and size. If you change the size of a figure, the original and resulting figures will not be congruent.

5.

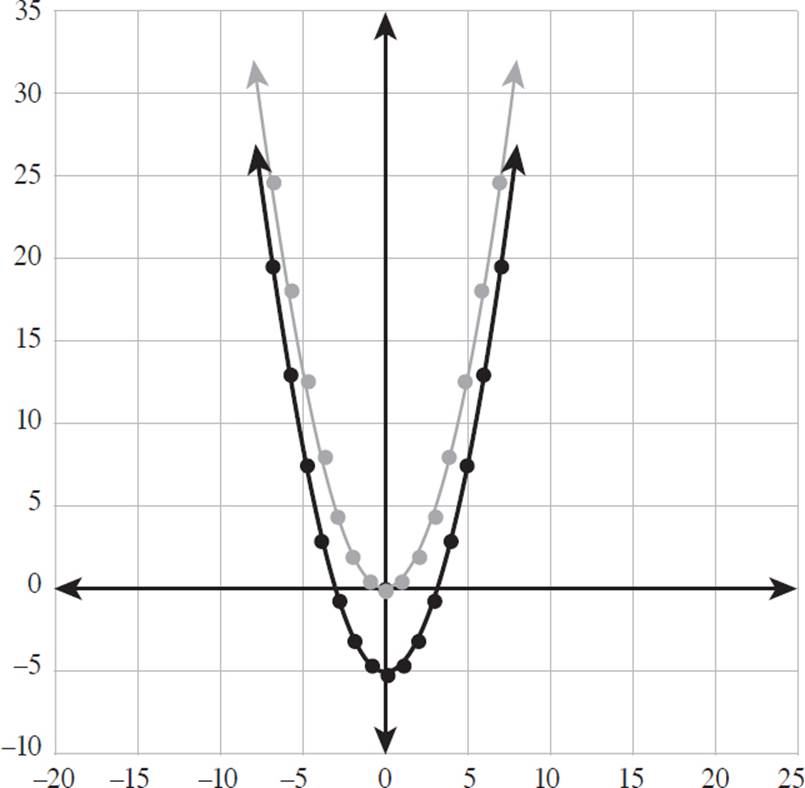
To graph f(x) − 5, shift the graph 5 units down. You do not have to plot an exhaustive number of points—just a few to allow you to complete your curve. The vertex (bottom) is a good place to start. It may help to place dots on the points you’re trying to move. Choose a point, and then place another dot 5 units directly below it. You may have to eyeball it. In our graph, 5 units is the height of one box.

Note: In this figure, the dots represent the points where x = 1, x = 2, and so on. This is just for reference; you did not need to figure all that out!

6. a.The center of the circle is located at (−4, 3) and since the radius is 1, the circle is originally located entirely in quadrant II. Reflecting the circle across the line x = 0 (the y-axis) flips the new circle into quadrant I.

b.The quadrilateral with the given points is a rectangle located in quadrant III. Reflecting the rectangle across the line y = x requires interchanging the x- and y-coordinates of the original pairs to obtain the new coordinates of (−2, −3), (−5, −3), (−5, −7), and (−5, −3). All four of these new coordinates still remain in quadrant III.

c.Though there are no given vertices for the triangle, it is stated that the triangle is located in quadrant IV. Reflecting the triangle across the line y = 1 (a horizontal line parallel to the x-axis passing through (0, 1)) moves the triangle into quadrant I.

d.The square with the given vertices is located in quadrant I. The line y = x is one of the lines of symmetry contained in the square, so the rotation produces the exact same square in the exact same location. To confirm, interchange the x- and y-coordinates given to arrive at the new coordinates of (1, 1), (5, 1), (1, 5), and (5, 5). All four of these new coordinates still remain in quadrant I.

7.H, I, N, O, S, X, and Z.

A rotational symmetry of 180° means that the figure (or letter, in this case) can be rotated upside down and still be the same as the original. The only letters that have this property are H, I, N, O, S, X, and Z.

8.

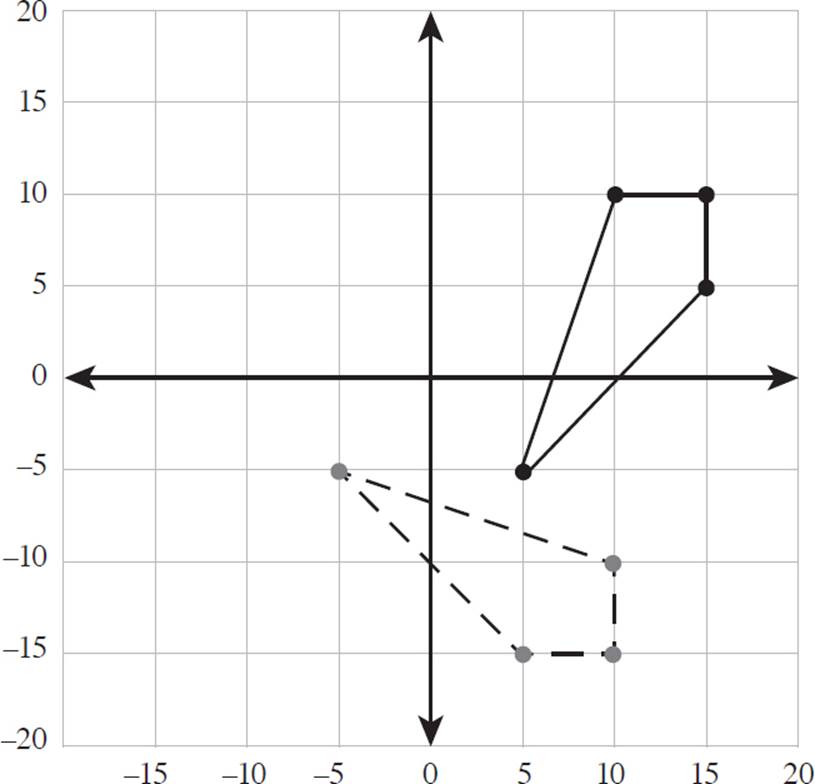
To rotate this figure, perform the rotation on one coordinate at a time. You can use the rectangle method described in the lesson, or the rotation rule R_270° (x, y) = (y, −x).

9.

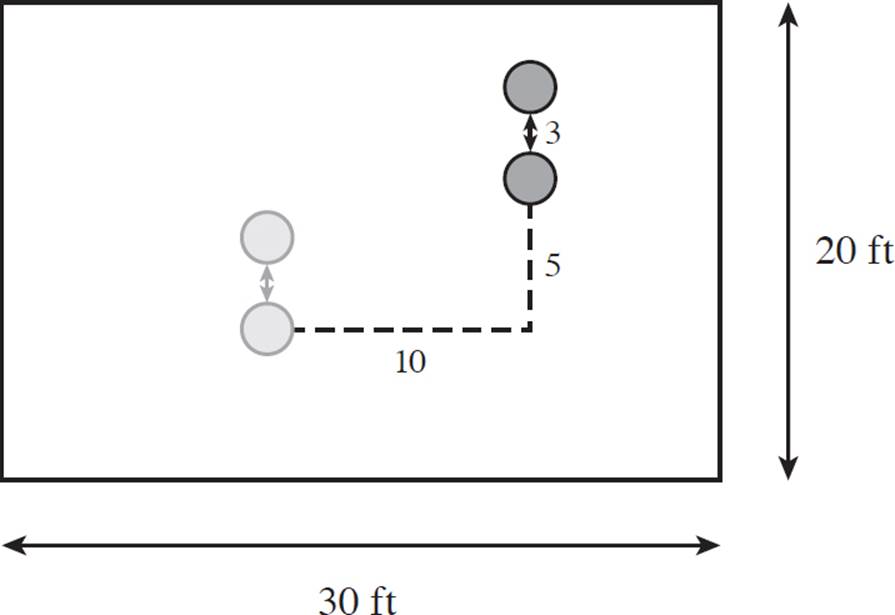
A 90° rotation would result in Dancer B being above Dancer A. The light grey circles in the figure represent the rotation from their original position. Then, the dancers will move 10 feet right and 5 feet up (note the direction for positive number translations).

You don’t have to measure this with a ruler…just sketch the location as close as you can get it, and label the distances represented by the translation.

Note: It’s also fine if you labeled the distances from a corner of the stage. For example, from the bottom left corner, Dancer A is 20 units right and 10 units up. Don’t worry about the size of the circles—consider their location to be measured from their centers.

10. Alex is correct (right hand).

When you stand in front of a mirror, your image is reflected, with the mirror itself acting as the line of reflection. If you hold up your right hand, the reflected image of the right hand will be directly in front of your “real” right hand.

Some people get confused when they’re imagining a person—not a reflection—standing in front of them. If you’re facing another person, this is represented by a rotation, not a reflection. Your right hand is on their left, and vice versa. But a mirror is not another person!

REFLECT

Congratulations on completing Chapter 1!

Here’s what we just covered.

Rate your confidence in your ability to:

•Perform translations, reflections, and rotations of figures

•Describe translations, reflections, and rotations of figures

•Write algebraic expressions for translations, reflections, and rotations of figures

•Perform and describe translations and reflections of functions

•Identify congruent and similar figures

•Classify figures as having reflectional symmetry and/or rotational symmetry

If you rated any of these topics lower than you’d like, consider reviewing the corresponding lesson before moving on, especially if you found yourself unable to correctly answer one of the related end-of-chapter questions.

Access your online student tools for a handy, printable list of Key Points for this chapter. These can be helpful for retaining what you’ve learned as you continue to explore these topics.