Math Workout for the GMAT

Part III Content and Strategy Review

Chapter 4 Assorted Topics 1

RATIOS

A ratio shows the relationship between two or more numbers, but it doesn’t tell you the actual values of those numbers. Suppose you have a recipe for margaritas that calls for 1 ounce of tequila and 1 ounce of triple sec for every 2 ounces of lime juice. You would say that the ratio of tequila to triple sec to lime juice is 1 : 1 : 2. But the recipe alone doesn’t tell you how much tequila you need for a particular batch of margaritas. For that, you also need to know an actual number, such as the total volume of the batch of margaritas.

The ratio box is an excellent tool to help you solve ratio problems. Make a grid with a row for each item in the ratio plus a row for the total. Use three columns: ratio value, multiplier, and actual value. The result will look like this.

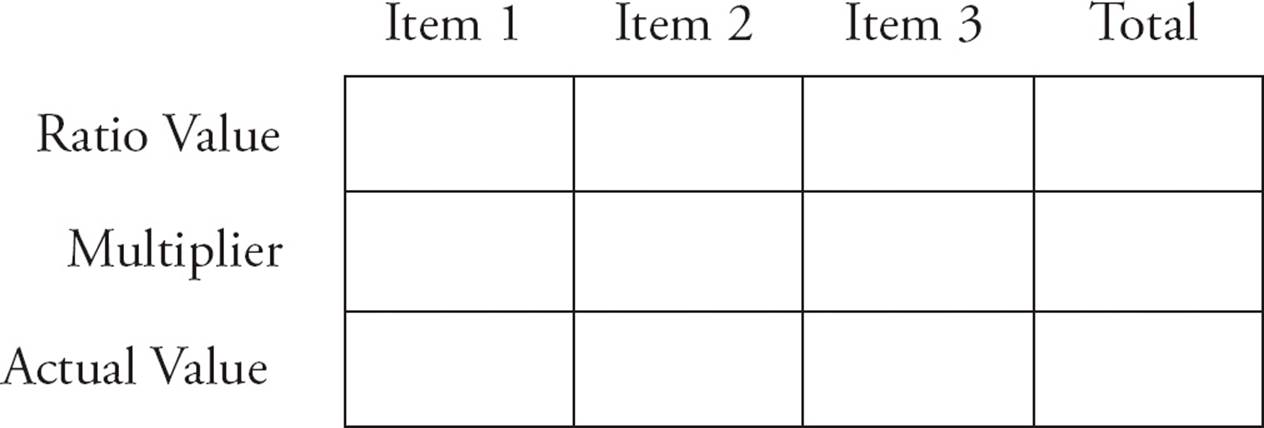
To use the ratio box, fill in all of the numbers from the problem. Then, find the multiplier by comparing the ratio value to the actual value for one item. This multiplier will be the same for all of the items. Just multiply the ratio value by the multiplier to find all of the other actual values. Look at this example.

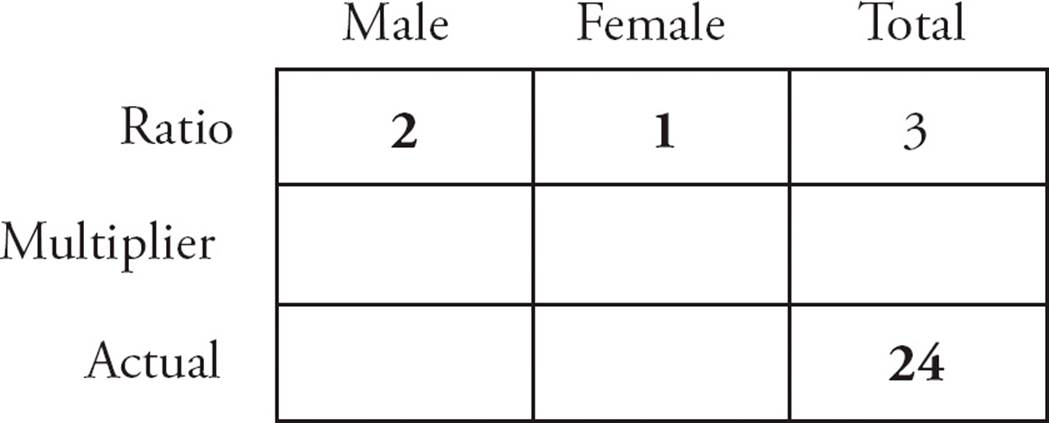
1.The Kosmic Kickers is a coed soccer team with 24 players on its roster. If the ratio of male players to female players is 2 to 1, how many female players are on the Kosmic Kickers’ roster?

First, draw a ratio box and fill in all the numbers from the problem. The ratio value for male players is 2. The ratio value for female players is 1. So the ratio total is 2 + 1 = 3. The roster contains 24 players, so that number goes in the box for actual total.

Here’s what you’ve got so far.

The next step is to find the multiplier. The ratio total is 3 and the actual total is 24. So the multiplier must be 8. Write 8 in the multiplier box. If you’re ever unsure of the multiplier, divide the total actual value by the total ratio value. The result is the multiplier.

To find the other actual values, multiply each ratio value by the multiplier, 8. Here’s what the completed box will look like:

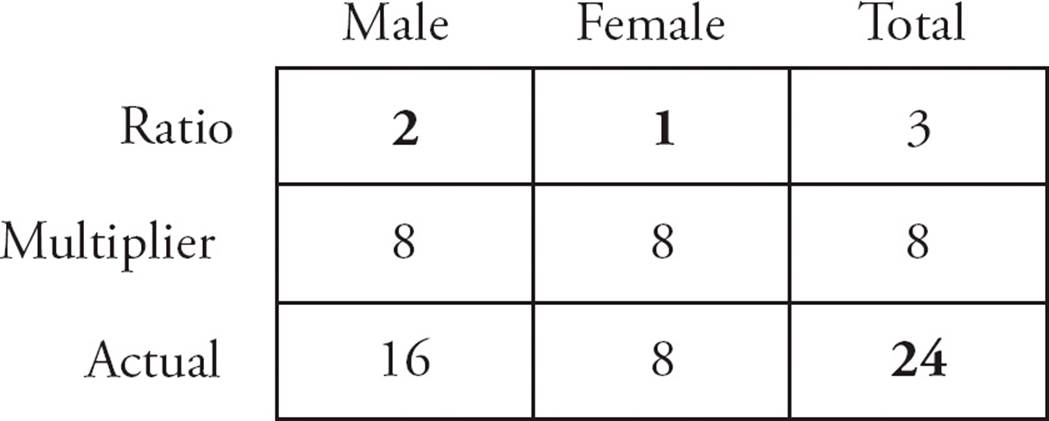
So the actual number of male players is 2 × 8 = 16 and the actual number of female players is 1 × 8 = 8. The correct answer is (C).

DRILL 1

Answers can be found on this page.

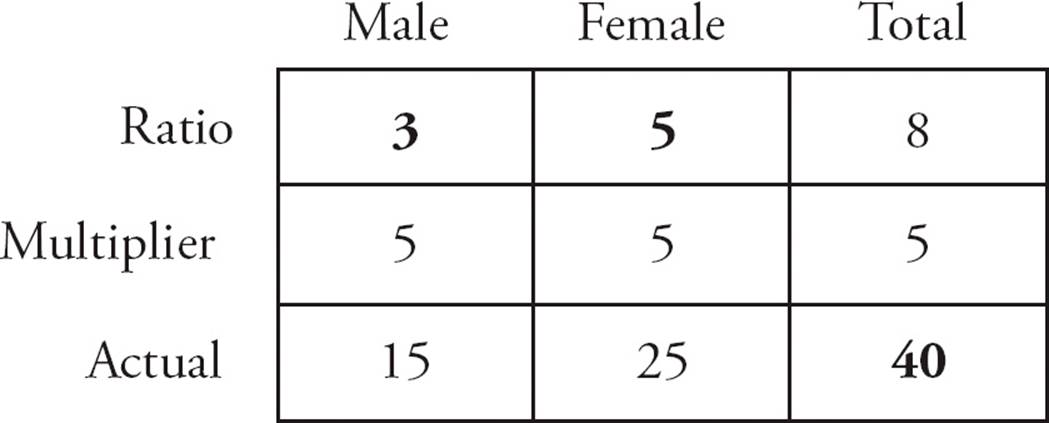
1.If the ratio of male students to female students in a philosophy class is 3 : 5, and there is a total of 40 students in the class, how many female students are in the class?

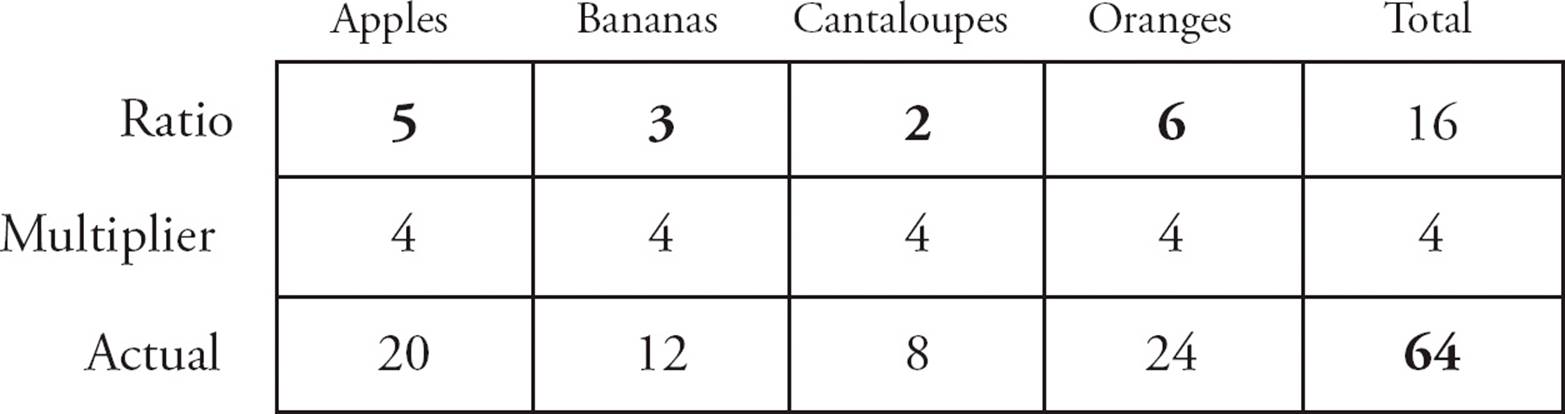
2.The ratio of apples, bananas, cantaloupes, and oranges at a fruit stand is 5 : 3 : 2 : 6, respectively. The total number of these fruits is 64. If 4 cantaloupes are added to the fruit stand, what is the new ratio of bananas to cantaloupes?

3.Fred has a jarful of nickels, dimes, and quarters, in the ratio of 2 : 5 : 10, respectively. If the total value of these coins is $15.50, how many dimes are in Fred’s jar?

PROPORTIONS

Proportions are very similar to ratios because they also show relationships between pairs of numbers. In fact, they’re pretty much the same as ratios; they’re just shown in a different way.

The way to solve a proportion question is to write two equal fractions, or ratios. Put the units in the same place in both fractions. For example, a question might ask, “If Carol can glaze 10 ceramic pots in 2 hours, how many pots can she glaze in 3 hours?” Set up the equal fractions as shown below.

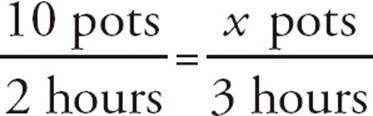
Notice that the number of pots is in the numerator of each fraction and the number of hours is in the denominator of each fraction. It’s important to set up your fractions in the same way. It doesn’t really matter which one (pots or hours) is in the numerator as long as it’s the same in both fractions. Because you don’t know the number of pots for the second fraction, use the variable x.

The next step is to cross-multiply the fractions. Multiply the denominator on the left by the numerator on the right and put the result on one side of the equals sign. Multiply the denominator on the right by the numerator on the left and put that on the other side of the equals sign. You end up with 10 × 3 = 2x. Solving the equation, you get x = 15, so Carol can glaze 15 pots in 3 hours.

DRILL 2

Answers can be found on this page.

1.Chris plays solitaire at the constant rate of 3 hands in 20 minutes. How many hands of solitaire can Chris play in 2 hours?

2.A bottle-capping machine caps 12 bottles per minute. How many minutes does the machine take to cap 30 bottles?

AVERAGES

An average tells you something about a group of people or things. The term arithmetic mean is also used to refer to averages. There are three numbers involved in any average question: the number of things in the group, the total amount, and the average amount. Given any two of these numbers, you can always find the third. The relationship of these three numbers is shown in the following formula:

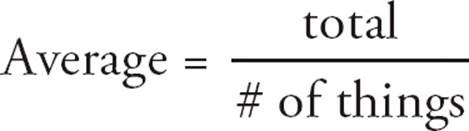
With this many vague numbers flying around, things get confusing. A tool called the average circle will help you keep everything organized, and as soon as you try a couple of problems, you’ll see that finding averages is pretty simple. Look at the diagram below. This gives you a place to put the three numbers for an average. Draw a separate circle for each average in the problem.

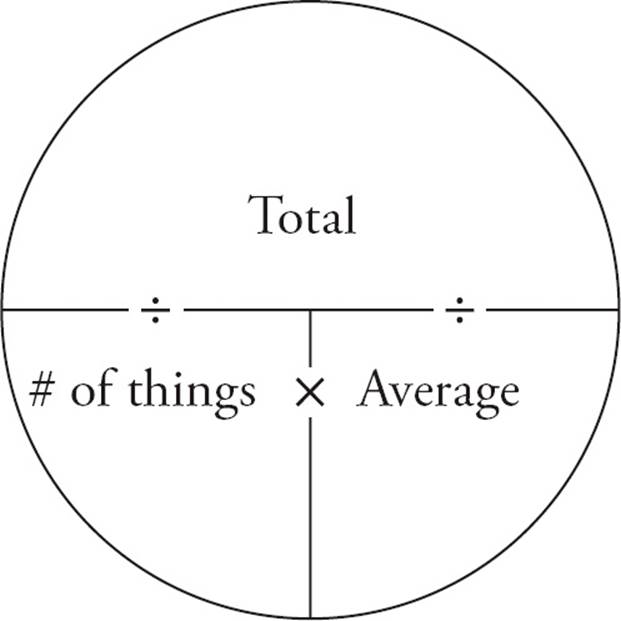
Fill in the two numbers the problem gives you and use that information to calculate the missing number. Notice that the line between the total and the other two numbers acts as the division line in a fraction. The total amount divided by the number of things gives you the average. The total amount divided by the average gives you the number of things. If you have the two bottom numbers, the number of things and the average, just multiply them to get the total amount. Try this problem.

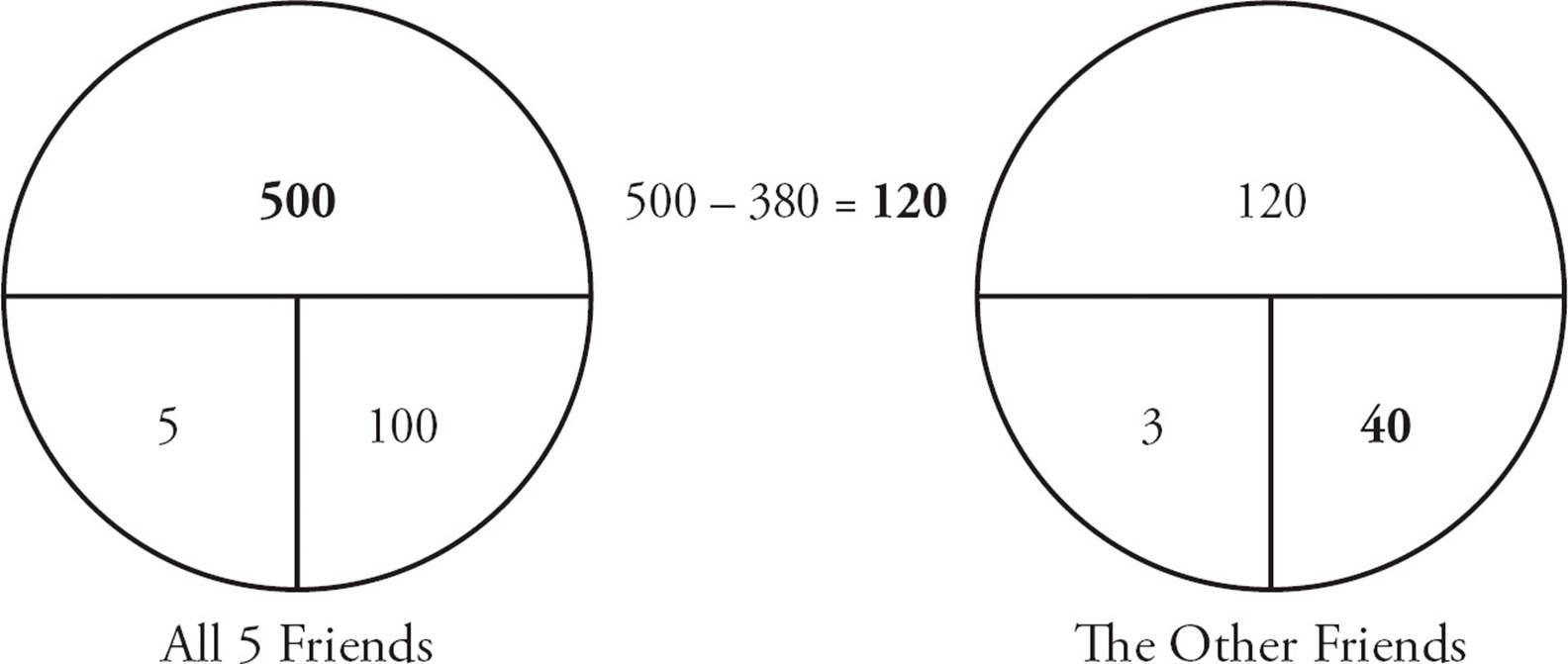
1.Five friends play blackjack in Las Vegas and lose an average of $100 each. If the losses of two of the friends total $380, what is the average loss of the other friends?

Draw two circles, one for the average of all five friends and one for the average of the other friends. In the first circle, fill in 5 for the number of things and $100 for the average. From this you can calculate the total loss, which is 5 × $100 = $500. For the second circle, fill in 5 − 2 = 3 for the number of things. The question asks for the average, so you first need to find the total loss of the other friends. You know the total lost by all five friends was $500 and that the two friends lost a total of $380, so the total loss of the other three friends must be $500 – $380 = $120. Fill that in for the total in the second circle. Now you can calculate the average loss of the three friends, which is 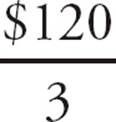= $40. The answer is (A).

Some questions require you to combine numbers from several circles. It’s okay to add and subtract the numbers of things and the total amounts, but never, ever, combine the averages directly. Averages must either be taken from the questions or calculated from the other two numbers in the circle. You can see this trap in the next example.

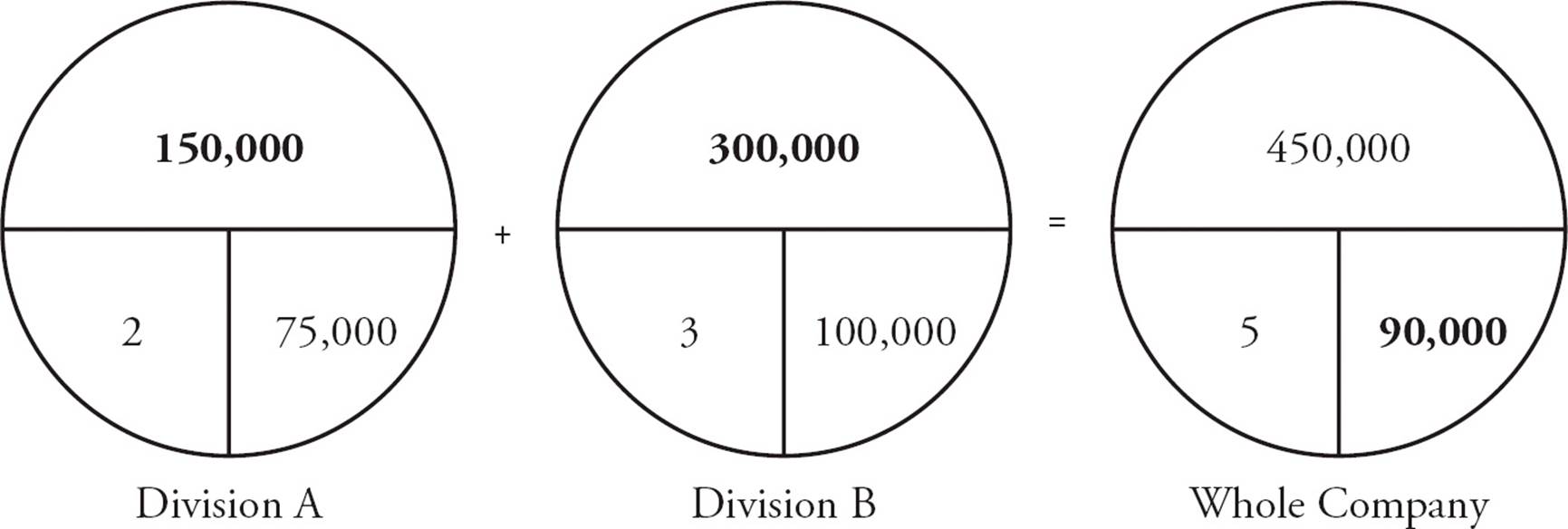
2.A company composed of two divisions is reviewing managerial salaries. The two managers in Division A of the company earn an average annual salary of $75,000. The three managers in Division B of the company earn an average annual salary of $100,000. What is the average salary of all the managers in the company’s two divisions?

Under no circumstances should you average the averages. That answer, $87,500, is there, but it’s a trap in this question. To correctly solve the problem, set up three circles: Division A, Division B, and the whole company. In Division A, the number of things is 2, the average is $75,000, and the total is 2 × $75,000 = $150,000. In Division B, the number of things is 3, the average is $100,000, and the total is 3 × $100,000 = $300,000. In the whole company, the number of things is 2 + 3 = 5, the total is $150,000 + $300,000 = $450,000. So the average is 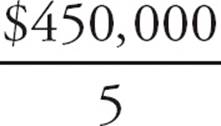=$90,000. The correct answer is (D).

DRILL 3

Answers can be found on this page.

1.The average (arithmetic mean) of four numbers is 5.5. When an additional number is included, the average of all five numbers is 6. What is the additional number?

2.A set of 10 numbers has an average (arithmetic mean) of 12. When a subset of numbers, which has an average of 15, is removed from the original set, the sum of the remaining numbers is 60. How many numbers remain from the original set?

GROUPS

Some GMAT problems deal with classifying a group of people or things into sub-groups. Many of these problems break the people into two classes, with some people in both classes and some people in neither class. Although these problems look complex, you can easily solve them by applying the following group formula:

Total = Class 1 + Class 2 – Both + Neither

Simply plug in the numbers the problem gives you and solve for the missing value. It’s possible that the problem will stipulate that everyone belongs to one class or the other. In that case, just plug in 0 for the Neither category. If the problem states that no one belongs to both classes, just use 0 for the Both value.

Here’s an example.

1.A company served bagels and coffee at a breakfast meeting. Of the 120 employees at the meeting, 50 ate bagels and 95 drank coffee. If 35 employees had both bagels and coffee, how many employees at the meeting had neither coffee nor bagels?

Plug the numbers into the formula and you get 120 = 50 + 95 − 35 + Neither. When you solve the equation, you get Neither = 10. The answer is (A). See, it’s much easier than it seemed at first.

Sometimes group problems get tough and the formula doesn’t help. These questions still feature two categories, but they will talk about the number of people that are and are not in each group. To solve these tough problems, you’ll need to set up a grid such as the one below.

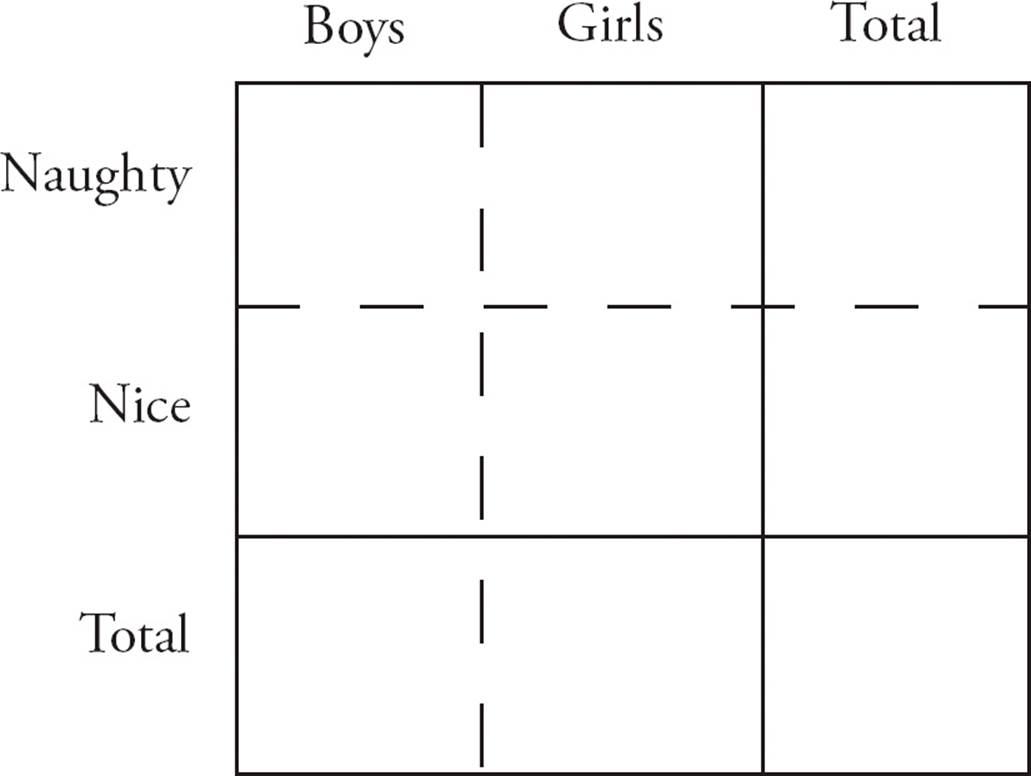
Each box in the grid shows the number of objects that match the labels above and to the left of the box. For example, the upper left box shows the number of naughty boys and the lower left box shows the total number of boys (naughty and nice). The middle box contains the number of nice girls. (Aha! So that’s how Santa keeps track of them all.)

In each row, add the two leftmost boxes to get the total for the rightmost box. In each column, add the two upper boxes to get the total for the bottom box. Given any two of the three numbers in a row or column, you can determine the third number through addition or subtraction. Look at this next example.

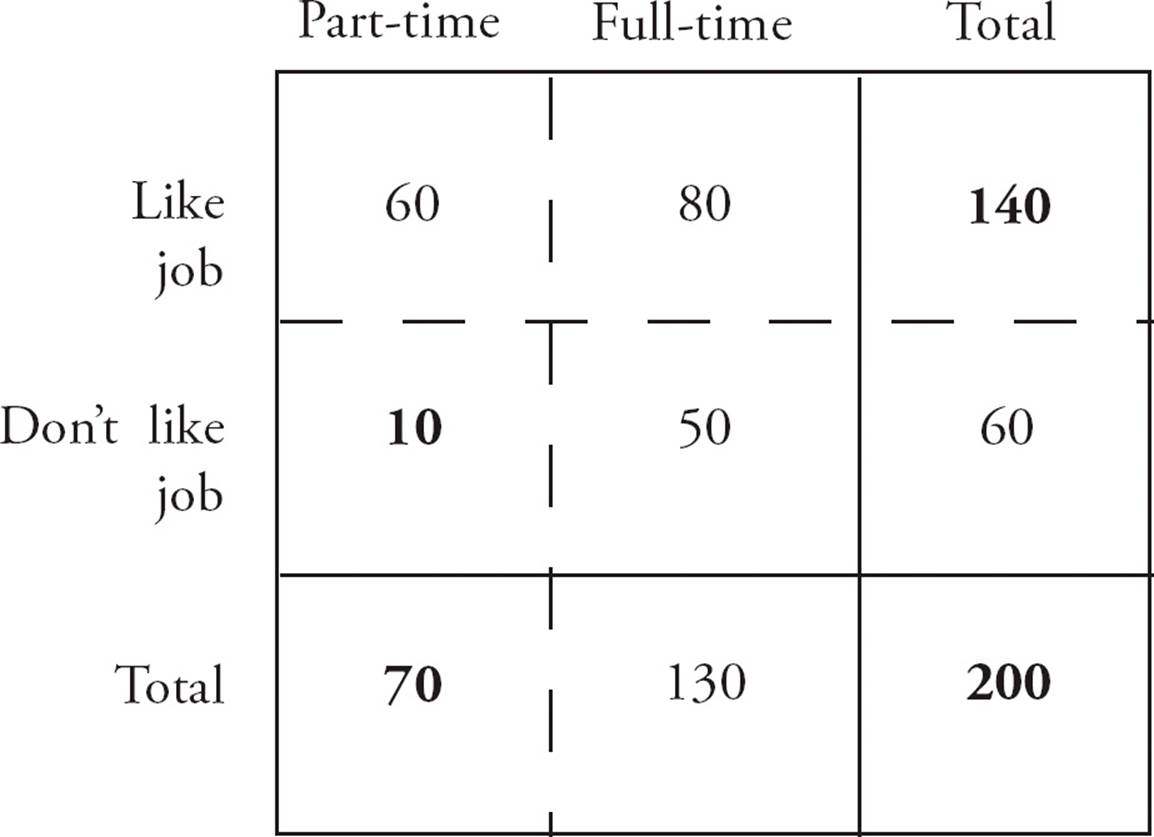
2.Of the 200 employees at Company A, 70 work part-time and the rest work full-time. If 140 of the employees like their jobs and 10 of the part-time employees don’t like their jobs, how many full-time employees like their jobs?

Set up the grid as shown below. Plug in the numbers provided in the question. These are shown in bold type in the diagram. Now you can figure out the other numbers. There are 70 part-time employees out of 200 total, so there must be 130 full-time employees. Since 10 of the 70 part-time employees don’t like their jobs, the other 60 must like their jobs. If 140 of the 200 employees like their jobs, the other 60 don’t like their jobs. Of the 140 employees who like their jobs, 60 are part-time, so the other 80 must be full-time. Of the 130 full-time employees, 80 like their jobs, so the other 50 don’t like their jobs. Every time you have two of the three numbers in a row or column, you can find the third number. The number of full-time employees who like their jobs is 80, so (C) is the correct answer.

DRILL 4

Answers can be found on this page.

1.The 2,000 students at College Q get one week for spring break. Each student takes the opportunity to travel to the beach, the mountains, or both. If 1,500 students take a trip to the beach and 700 take a trip to the mountains, how many students go to both the beach and the mountains?

2.The 25 players on the Little Sluggers baseball team are supposed to take their caps and gloves to each game. At the first game of the season, 22 players took their caps and 18 took their gloves. If 6 players took their caps but not their gloves, how many players took neither cap nor glove to the first game?

INTEREST

One of the few business-related topics that the GMAT tests is interest rates. To calculate the interest earned in a year, multiply the initial amount of money (also called the principal) by the percentage interest rate. For example, if $500 is deposited for one year in a savings account that earns 4% interest, then the account will earn $500 × 4% = $20 in interest for that year. So the total amount in the savings account after one year is $500 + $20 = $520. This type of interest calculation is sometimes called simple interest.

When the GMAT does test you on interest, the problem usually involves compound interest. Either the money will earn interest for a period longer than a year, or the interest will compound more frequently than once per year. For example, suppose that $500 is deposited for ten years in a savings account earning 4% interest. In the first year, the account earns $20 in interest, so during the second year, the account earns interest on $520, not $500. In the third year, the principal is even greater. Thus, the account earns interest on the interest. While this is great for your IRA account, it can make GMAT questions a little tougher.

Fortunately, you can usually avoid calculating the precise amount of compound interest. Instead, use Ballparking to find the answer. Start by finding the simple interest, which is, well, pretty simple. Then find an answer that’s a little bit bigger. Look at the next example.

1.Allan deposits $1,000 into a bank account that pays 3% interest annually. If he makes no other deposits or withdrawals, approximately how much money is in the account after four years?

Start by calculating the simple interest. The interest for one year is $1,000 × 3% = $30. For four years, that’s $120 in simple interest, which makes the total amount in the account $1,000 + $120 = $1,120. Look for the answer that’s a little bit bigger. The answer has to be (D).

Every once in a while, you may need to know the formula for compound interest. You probably won’t need to make the calculation, but you may need to set up the equation. The formula is

Total amount = principal × (1 + r)^t,

in which r is the interest rate (expressed as a decimal) for the compounding period and t is the number of compounding periods. You’ll need the formula for this next example.

2.Amy deposits $100 into an account that pays 8% interest, compounded semiannually. She makes no other deposits or withdrawals. Which of the following expresses the amount of money the account will contain in 2 years?

You use 0.04 for r because the account earns 4% over six months; the 8% rate is for a full year. You use 4 for t because two years contains four six-month periods. So the correct answer is (B). Notice that you’re not going to complete the calculation. You’d need a calculator for that and it’s not necessary; just setting up the equation is enough.

DRILL 5

Answers can be found on this page.

1.Mark deposits $1,000 into a bank account that pays annual interest of 7%. If he makes no other deposits or withdrawals, approximately how much interest has the account earned after four years?

2.Gilbert deposits $200 into a bank account that earns interest at the rate of 8%. He makes no further transactions other than a $100 withdrawal after 3 years. Approximately how much money is in Gilbert’s account after he makes the withdrawal?

Comprehensive Assorted Topics 1 Drill

Answers can be found on this page.

Remember!

For Data Sufficiency problems in this book, we do not supply the answer choices. The five possible answer choices are the same every time.

1.Three hungry children, Sharon, Carol, and Elinor, agree to divide a batch of cookies in the ratio 3 : 5 : 7, respectively. If Sharon’s share was 15 cookies, how many cookies were in that batch?

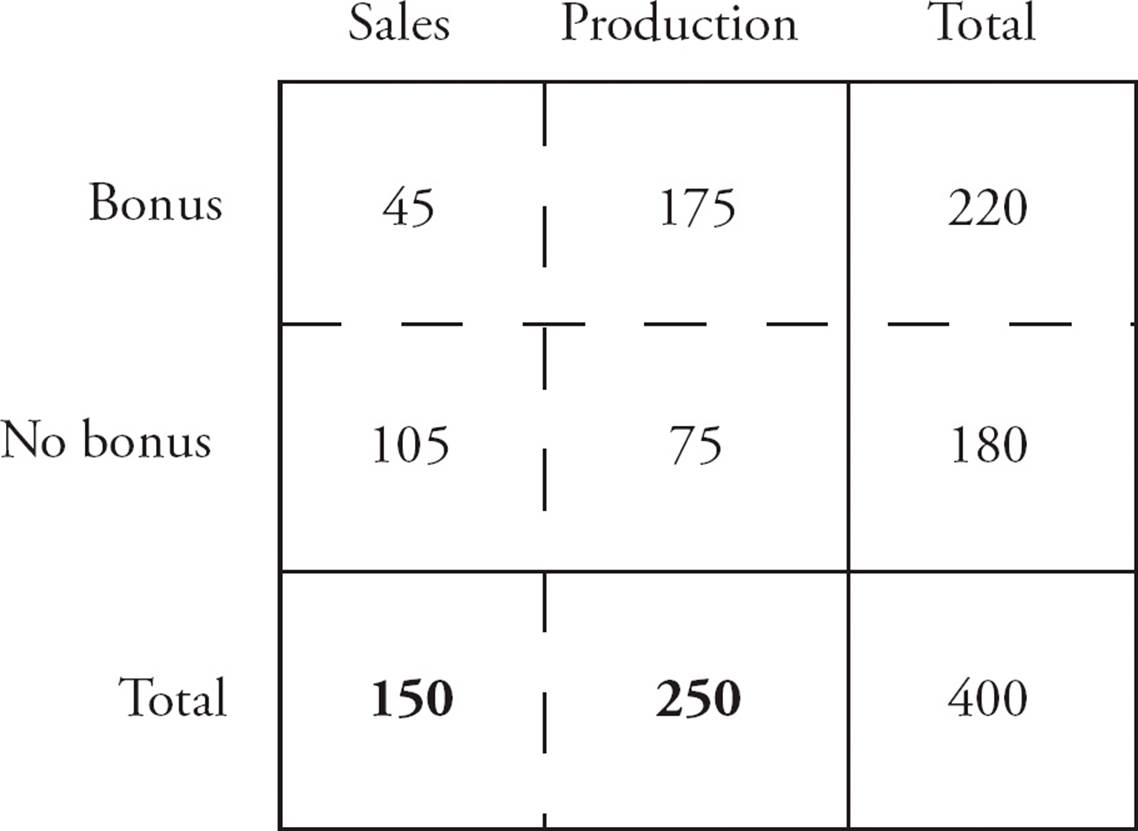
2.A company consists of two departments: sales and production. If 30 percent of the 150 employees in the sales department received a holiday bonus and 70 percent of the 250 employees in the production department received a holiday bonus, what percent of all employees did not receive a holiday bonus?

3.What is the ratio of a to b ?

(1) a = b + 7

(2) 3a = 4b

4.All working at the same constant rate, 8 bartenders can pour 96 shots per minute. At this rate, how many shots could 3 bartenders pour in 2 minutes?

5.The average (arithmetic mean) of 2, 4, 6, and 8 equals the average of 1, 3, 5, and

6.The latest model of space shuttle can achieve a maximum speed of 25 miles per second. This maximum speed is how many miles per hour?

7.How many of the employees at Company X have life insurance?

(1) There are 300 employees at Company X.

(2) The ratio of employees with life insurance to employees without life insurance is 1 : 5.

8.What is x ?

(1) The ratio of x : y is 1 : 3.

(2) The ratio of y : z is 1 : 2.

9.The five starting players on a basketball team score points in the ratio of 1 : 1 : 2 : 3 : 4. If the starters score a total of 77 points in a particular game, how many points did the highest-scoring starter score?

10.If $1 was invested at 4% interest, compounded quarterly, the total value of the investment, in dollars, at the end of three years would be

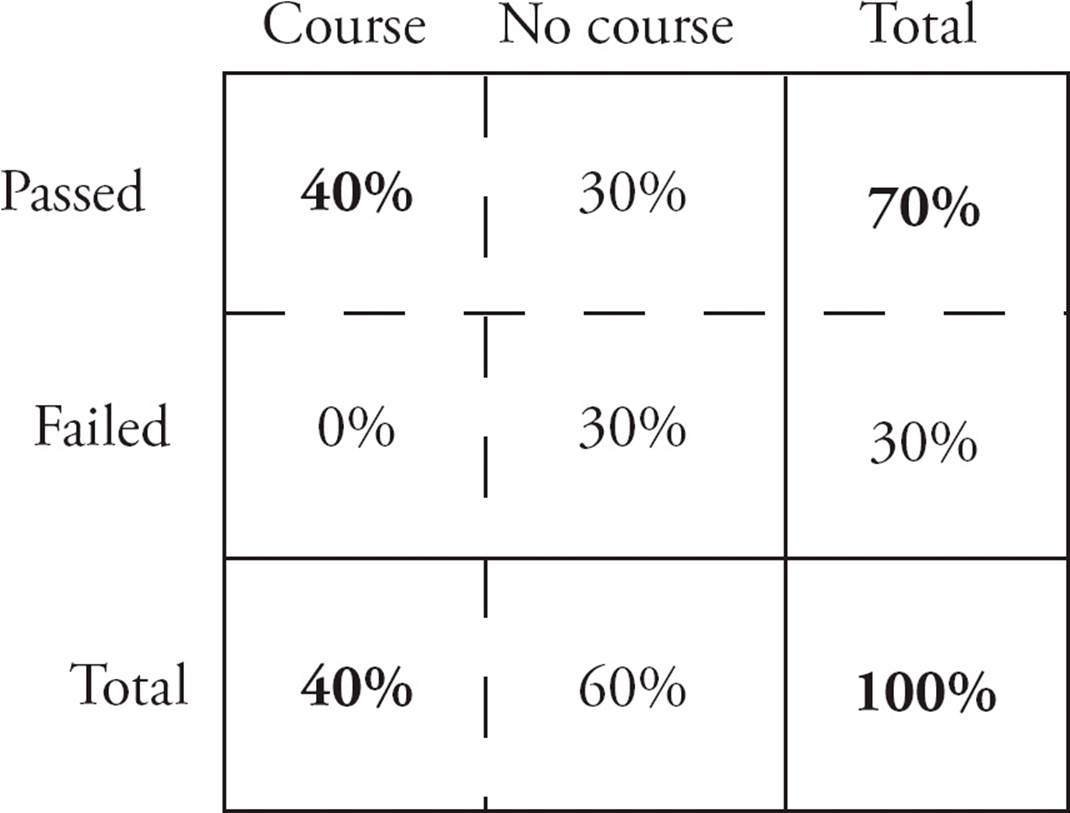
11.Among a group of teenagers taking a driving test, 40% took a driver’s education course. If 70% of the teenagers pass the driving test and all of those who took a driver’s education course passed the test, what percent of the teenagers who did not take a driver’s education course failed the test?

12.If a laser printer can print 2 pages in 10 seconds, how many pages can it print in 3 minutes at the same rate?

13.If the average (arithmetic mean) of three positive integers is 35, how many of the numbers are greater than 10 ?

(1) The sum of two of the numbers is 75.

(2) None of the numbers is greater than 40.

14.Greg is training for a marathon by running to and from work each day, a distance of 12 miles each way. He runs from home to work at an average speed of 6 miles per hour and returns at an average speed of 4 miles per hour. What is Greg’s average speed, in miles per hour, for the round trip?

15.Each baseball team in a league has a roster of players in the ratio of 2 pitchers for every 3 fielders. If each team has a total of 25 players on its roster and there are 12 teams in the league, the number of pitchers in the league is how much less than the number of fielders in the league?

16.The first-year MBA class at XYZ University is composed of 60 male students and 40 female students. How many male students from the first-year class are taking economics?

(1) Fifty percent of the first-year class is taking economics.

(2) 10 female students from the first-year class are not taking economics.

17.If the current population of country Z is 200,000 people and the population grows by 3% every year, which of the following expresses the population of Country Z in 5 years?

18.The 250 students enrolled at ABC University are taking undergraduate courses, graduate courses, or both. How many students are taking graduate courses?

(1) 200 students are taking undergraduate courses.

(2) 50 students are taking both undergraduate and graduate courses.

19.A total of 120 investment advisors work at a particular financial services firm, 30 in bonds and the rest in equities. Fifty percent of the investment advisors are board-certified. If one third of the equities advisors are board-certified, how many bonds advisors are not board-certified?

20.How many people contributed to the Charity Y ?

(1) The average contribution to Charity Y was $100.

(2) Charity Y collected a total of $47,000 in contributions.

21.The average of two numbers is 108. What is the value of the greater number?

(1) The lesser number is 72.

(2) The ratio of the two numbers is 1 : 2.

Challenge!

Take a crack at this high-level GMAT question.

22.A certain compound X has a ratio of 2 oxygen for every 5 carbon. Another compound Y has a ratio of 1 oxygen for every 4 carbon. If a mixture of X and Y has a ratio of 3 oxygen for every 10 carbon, what is the ratio of compound X to compound Y in the mixture?

ANSWERS AND EXPLANATIONS

Drill 1

1.EStart by drawing a ratio box like the one shown below. Then, fill in the numbers from the problem (shown in bold in the diagram). In the ratio, you have 3 male students and 5 female students, for a ratio total of 3 + 5 = 8 students. Given the actual total, 40 students, the multiplier is 40 ÷ 8 = 5. Multiply each of the ratio values by 5 to find the actual values. The number of female students is 5 × 5 = 25. Choose (E).

2.CSet up a ratio box with the numbers from the problem (shown in bold in the diagram below). The ratio total for the fruit is 5 + 3 + 2 + 6 = 16. Given the actual total of 64 pieces of fruit, you can find the multiplier, which is 64 ÷ 16 = 4 . Multiply all the ratio numbers by 4 to find all the actual numbers: 20 apples, 12 bananas, 8 cantaloupes, and 24 oranges. Now, add 4 cantaloupes for a new total of 12 cantaloupes. The new ratio of bananas to cantaloupes is 12 : 12, which reduces to 1 : 1. Choose (C).

3.BSet up a ratio box as shown below. Notice that you need to include the value of the coins as well as the number of coins. The total ratio value of the coins is $3.10 (the value of 2 nickels, 5 dimes, and 10 quarters). Given the total actual value of $15.50, you can find the multiplier, which is $15.50 ÷ $3.10 = 5. Multiply all the ratio values by 5 to get the actual values. So the number of dimes is 5 × 5 = 25. Choose (B).

Drill 2

1.DSet up the two equivalent fractions as shown below. Notice that you need to change 2 hours to 120 minutes. You must use the same units in both fractions. Then cross-multiply to get 3 × 120 = 20x, which simplifies to 360 = 20x. Divide both sides by 20 to get x = 18. Chris can play 18 hands of solitaire in 2 hours. Choose (D).

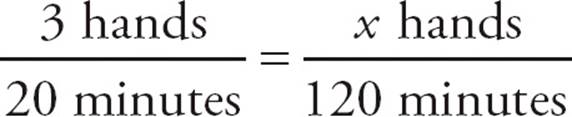
2.ASet up the equivalent fractions as shown below. Notice that the variable is in the denominator of the fraction. That’s okay as long as the fractions are consistent. Cross-multiply to get 12x = 30 × 1 or simply 12x = 30. Divide both sides by 12 to get x = 2.5. Choose (A).

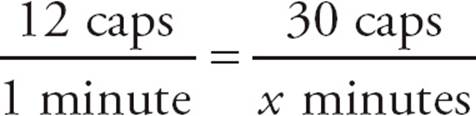
Drill 3

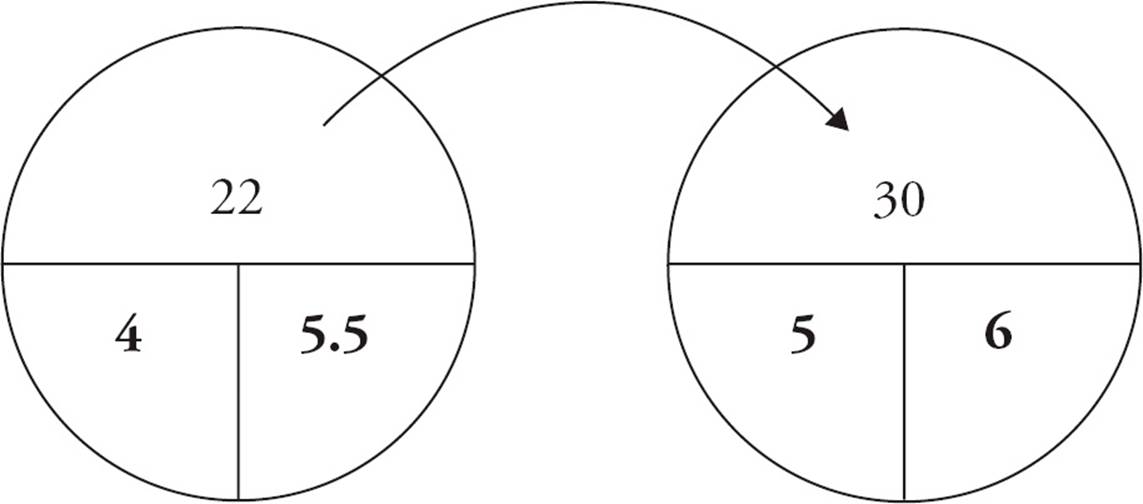
1.CDraw two average circles, one for the set of four numbers and one for the set of five numbers. Fill in the numbers provided in the problem (shown in bold in the diagram below). In the set of four numbers, the total is 4 × 5.5 = 22. In the set of five numbers, the total is 5 × 6 = 30. So the additional number must be 30 − 22 = 8. Choose (C).

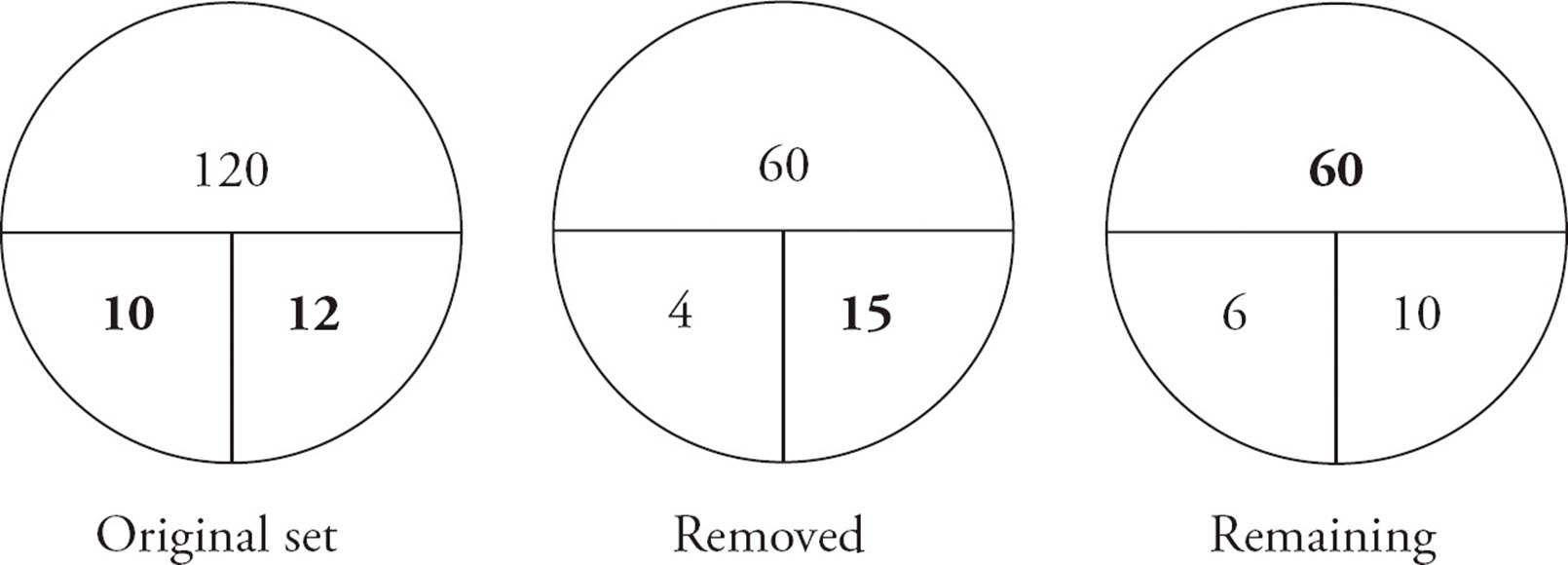
2.DDraw three average circles: the original set, the removed subset, and the remaining members of the original set. Fill in the numbers from the problem (shown in bold in the diagram below). In the original set, the total is 10 × 12 = 120. The total of the removed numbers is the difference between the totals of the original set and the remaining numbers, or 120 − 60 = 60. Given the average of 15, the number of numbers that were removed is 60 ÷ 15 = 4. So the number of remaining numbers is 10 − 4 = 6. Choose (D).

Drill 4

1.ASet up the group formula with the numbers from the problem: 2,000 = 1,500 + 700 – Both + 0. Use the 0 for Neither because the problem states that every student takes a trip. Simplifying the equation, you get 2,000 = 2,200 – Both, and the solution is Both = 200. Choose (A).

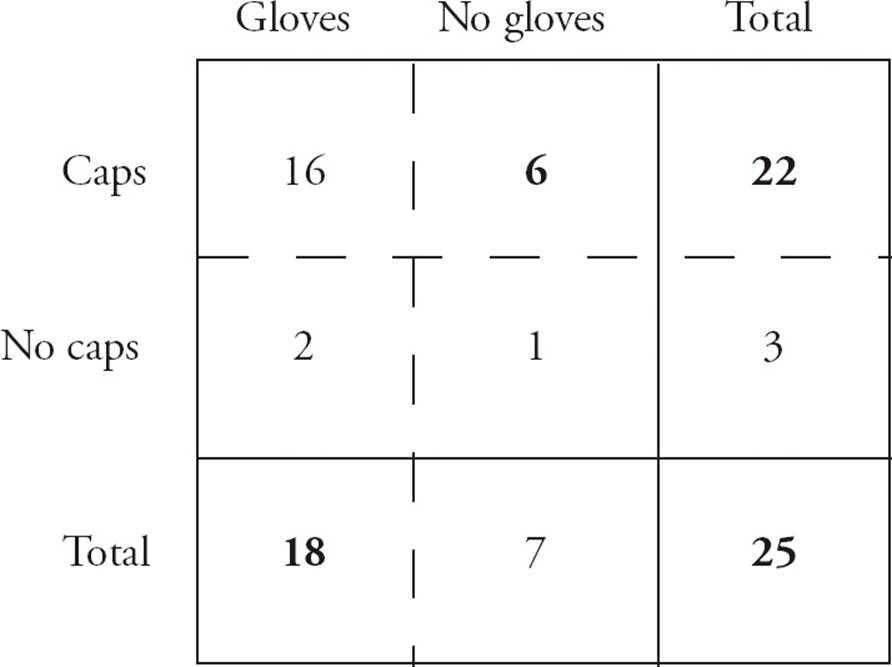
2.ASet up the grid as shown below. The numbers given in the problem are shown in bold. Of the 25 players, 22 took their caps, so 3 did not. You know 18 players took gloves, so 7 did not. Of the 22 players with caps, 6 forgot gloves, so 16 remembered to take gloves. Of the 18 with gloves, 16 took caps, so 2 didn’t. Of the 3 who did not take caps, 2 took gloves, so 1 player took neither a cap nor a glove. Just where did he think he was going, anyway? Choose (A).

Drill 5

1.BSimple interest would be 4 × 7% × $1,000 = $280. The interest compounds (more than one year), so choose the next higher answer. Choose (B).

2.DGilbert made his $100 withdrawal after it earned interest, not before then. Calculate the interest on $200, and then subtract $100 from the total. Simple interest for three years would be 3 × 8% × 200 = $48, for a total of 200 + 48 − 100 = $148. So choose the answer that’s a little higher because the interest compounds. Choose (D).

Comprehensive Assorted Topics 1 Drill

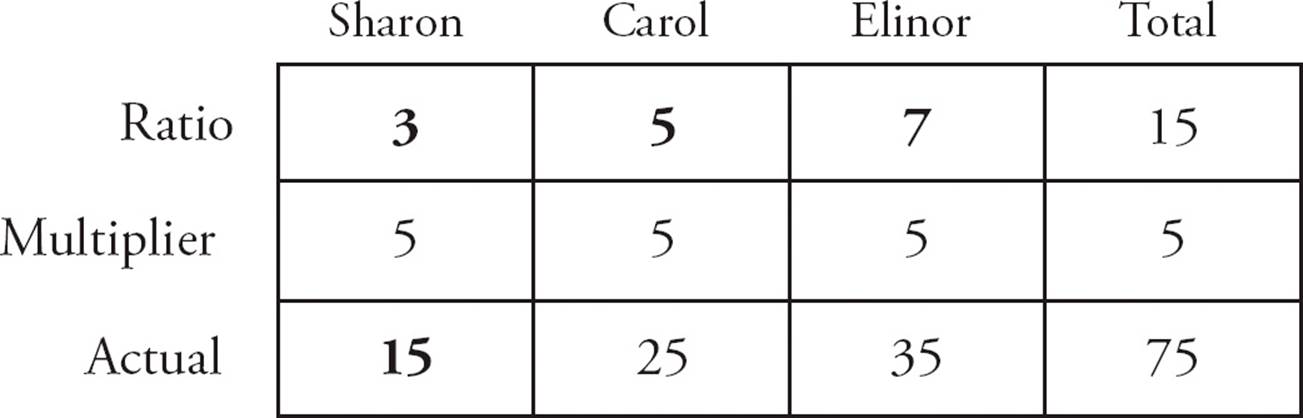
1.BSet up a ratio box as shown below. The ratio total is 3 + 5 + 7 = 15. Sharon’s actual value is 15 and her ratio value is 3, so the multiplier is 15 ÷ 3 = 5. Multiply all of the ratio values by 5 to get the actual values. So the actual total is 15 × 5 = 75. Choose (B).

2.BSet up a grid as shown below. The number of sales employees receiving a bonus is 30% × 150 = 45, so the number of sales employees not receiving a bonus is 150 − 45 = 105. The number of production employees receiving a bonus is 70% × 250 = 175, so the number of production employees not receiving a bonus is 250 − 175 = 75. So 105 + 75 = 180 employees did not receive a bonus. The percent of all employees not receiving a bonus is 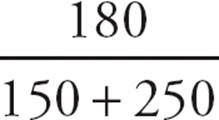= = 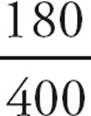= 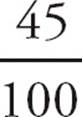45%. Choose (B).

3.BStart with Statement (1). You can’t determine the ratio of a to b. If a = 8 and b = 1, the ratio of a to b is 8 : 1. If a = 9 and b = 2, the ratio is 9 : 2. You can’t answer the question, so narrow your choices to (B), (C), and (E). Try Statement (2). You can rewrite this equation as = , so the ratio of a to b is 4 : 3. You can answer the question, so choose (B).

4.EYou can set up equivalent fractions for this proportion: 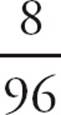= . Cross-multiply to get 8x = 3 × 96 or 8x = 288. Solving the equation, you get x = 36. However, this is just the number of shots 3 bartenders can pour in 1 minute. So in 2 minutes, 3 bartenders can pour 2 × 36 = 72 shots. Choose (E).

5.DSet up two average circles. In the first circle, the total is 2 + 4 + 6 + 8 = 20. The number of things is 4, so the average is 20 ÷ 4 = 5. In the second circle, the average is 5 (the same as the first circle) and the number of things is 4. Therefore, the total should be 4 × 5 = 20. Now you know that the total in the second circle is 1 + 3 + 5 + x = 20. Solve for x and you get 11. Choose (D).

6.ESet up the proportion: 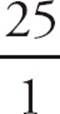= 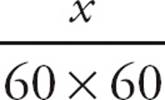. You use 60 × 60 for the number of seconds because there are 60 seconds in a minute and 60 minutes in an hour. Cross-multiply to get x = 25 × 60 × 60 or x = 90,000. Choose (E).

7.CStart with Statement (1). This tells you only the total number of employees, not anything about the number that have life insurance. You can’t answer the question, so narrow your choices to (B), (C), and (E). Look at Statement (2). A ratio doesn’t tell you anything about actual numbers unless you have another actual number to go with it (so you can find the multiplier). You can’t answer the question, so eliminate (B). Try Statements (1) and (2) together. Now you have the ratio as well as an actual number. You can use the actual number to find the multiplier, and then use the multiplier to find all the other actual values. You can answer the question, so choose (C).

8.ELook at Statement (1). The ratio alone won’t help you find the actual values of the variables. You can’t answer the question, so narrow your choices to (B), (C), and (E). Try Statement (2). This doesn’t even mention x, so you can’t answer the question. Eliminate (B). Try Statements (1) and (2) together. You could set up a ratio for x to z. But you can’t find the actual value of x without another actual value to go with the ratio. You can’t answer the question, so choose (E).

9.ESet up a ratio box as shown below. The numbers from the problem are shown in bold. The ratio total is 1 + 1 + 2 + 3 + 4 = 11. The actual total is 77, so the multiplier is 77 ÷ 11 = 7. Multiply all of the ratio values by 7 to find the actual values. The actual value for the highest-scoring starter is 4 × 7 = 28. Choose (E).

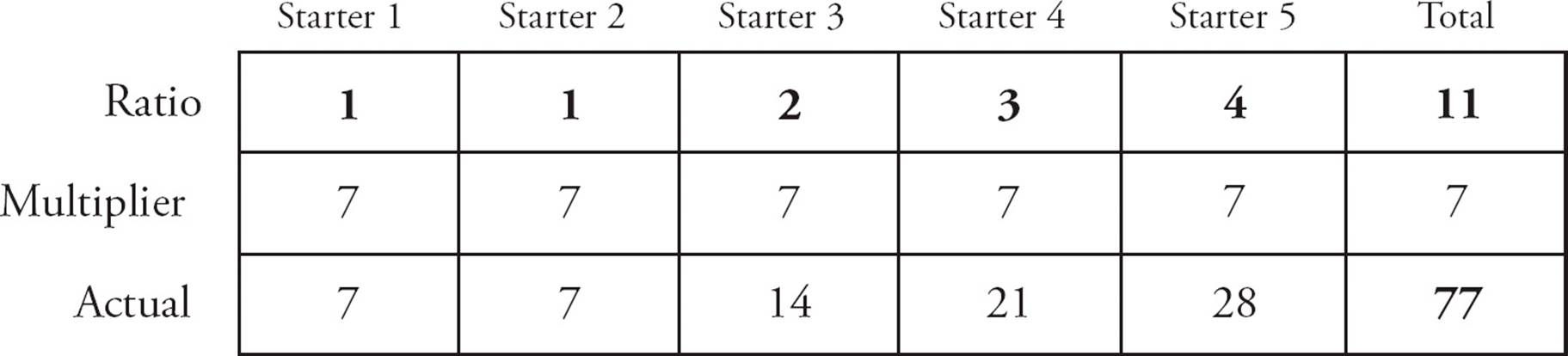
10.DYou just need to insert the numbers into the compound interest formula: (1 + r)^t. Interest compounds four times per year at a 4% rate, so r = 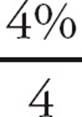= 1% = 0.01. The interest compounds four times per year for three years, so there are 12 interest periods. That means t = 12. The completed formula is (1.01)¹². Choose (D).

11.DSet up a grid as shown below. Plug in the numbers provided in the question (bold type in the diagram below). Note that you don’t have actual numbers, so just use 100% for the total and the appropriate percentages for the other boxes. Start finding the other numbers. 40% took the course, so 60% didn’t. 70% passed the test, so 30% didn’t. All of the course takers (40%) passed, so 0% took the course and failed. A total of 70% passed, so 70% − 40% = 30% of teenagers passed and didn’t take a course. That leaves 60% − 30% = 30% who did not take the course and failed. Out of the 60% of teenagers who didn’t take the course, 30% of teenagers failed, but that’s 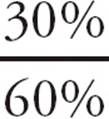= 50% of those who didn’t take the course. Choose (D).

12.DSet up the proportion: 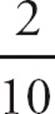= 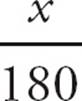. You need to keep the units consistent in both fractions, so use 180 seconds for the 3 minutes. Cross-multiply to get 10x = 2 × 180. That’s 10x = 360, so x = 36. Choose (D).

13.BStart with Statement (1). The sum of the three numbers is 3 × 35 = 105. You can calculate that the third number is 105 − 75 = 30, definitely more than 10. However, you cannot tell whether one or two of the other numbers is more than 10. They might be 40 and 35, or they might be 1 and 74. You can’t answer the question, so narrow your choices to (B), (C), and (E). Try Statement (2). This means that the smallest any number could be is 105 − 40 − 40 = 25. If you try to make a number smaller than 25, at least one of the numbers will be greater than 40. All three numbers must be more than 10. You can answer the question, so choose (B).

14.COn the way to work, Greg needs 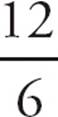= 2 hours to complete the trip. On the way home, Greg needs 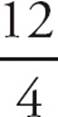= 3 hours to complete the trip. So he travels 12 + 12 = 24 miles in 2 + 3 = 5 hours. That’s an average speed of 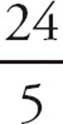= 4.8 miles per hour. Choose (C). If you chose (B), you fell for the obvious answer trap of averaging the averages.

15.CYou need to use an expanded ratio box, like the one shown below. The ratio total is 2 + 3 = 5 players. There are 25 players on a team, so the multiplier for ratio to team is 25 ÷ 5 = 5. Multiply all of the ratio values by 5 to find the actual team values. There are 12 teams in the league, so the multiplier for team to league is 12. Multiply all of the team values by 12 to get the league values. The number of fielders in the league is 3 × 5 × 12 = 180. The number of pitchers in the league is 2 × 5 × 12 = 120. So the difference is 180 − 120 = 60. Choose (C).

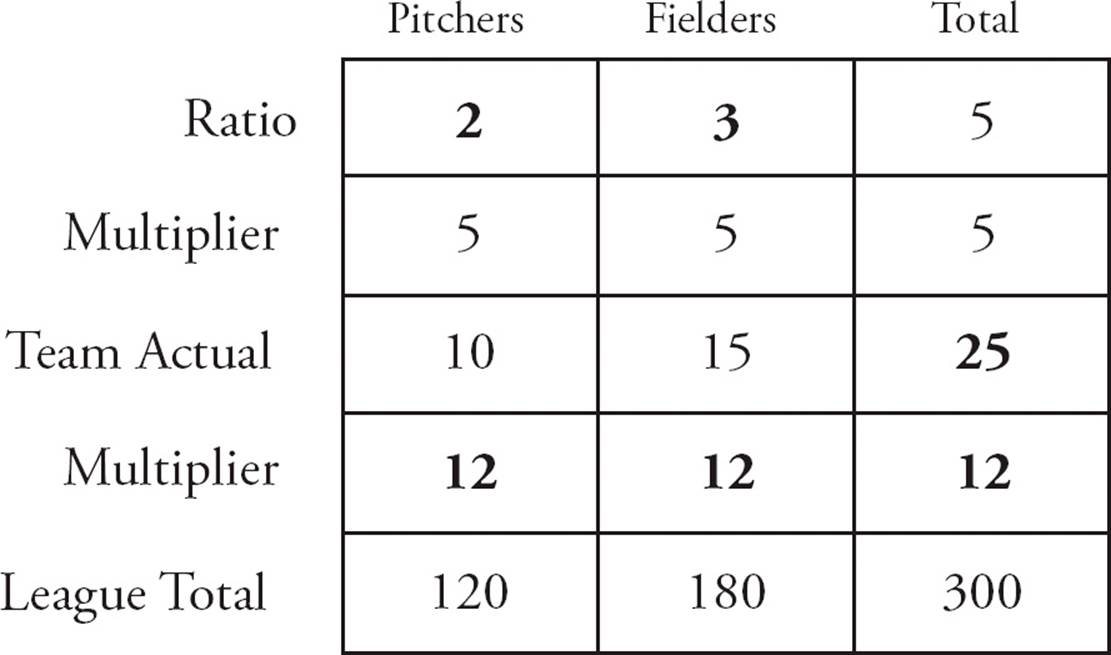
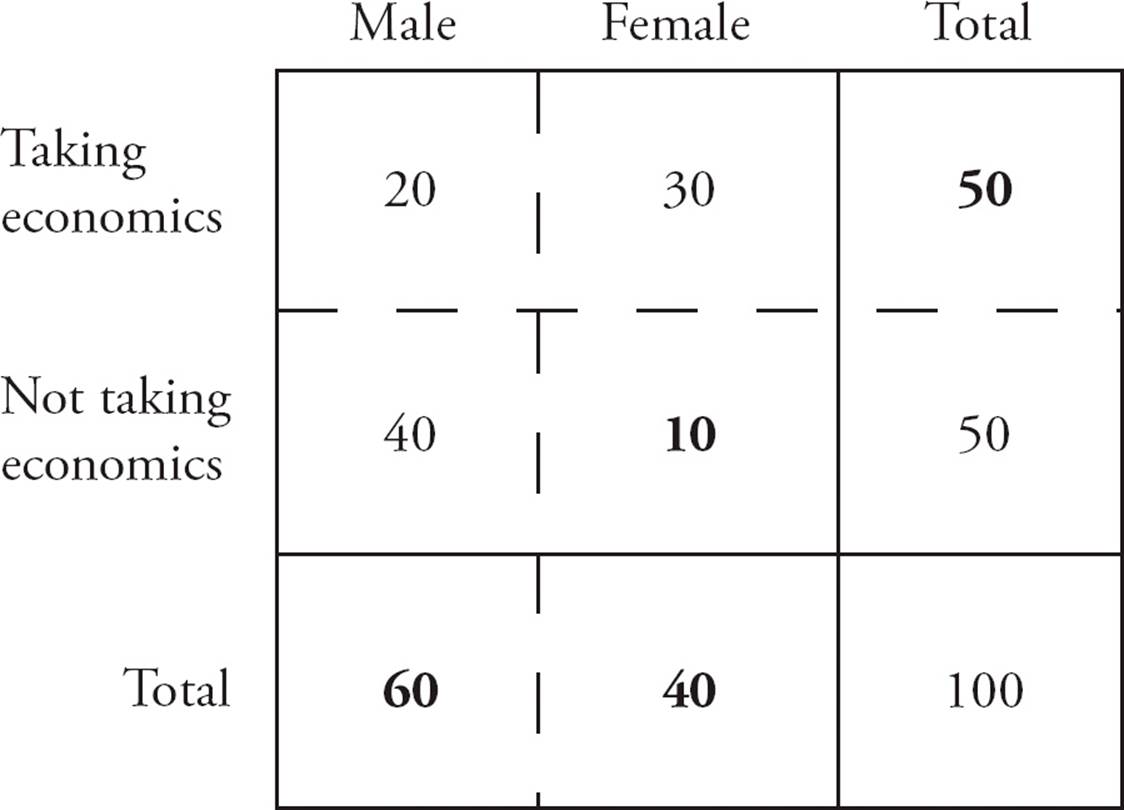
16.CYou should set up a group grid as shown below. Start with Statement (1). This allows you to fill in 50 students for economics and 50 students not for economics. But you don’t have two numbers anywhere that you can use to find a third number. You can’t answer the question, so narrow your choices to (B), (C), and (E). Try Statement (2). Erase any numbers you filled in from Statement (1). Now you can find that 40 − 10 = 30 female students are taking economics. But you can’t find how many male students are or are not taking economics because you don’t have 2 of the 3 numbers. You can’t answer the question, so eliminate (B). Try Statements (1) and (2) together. Now you can find all the numbers because you have 2 out of every 3 numbers. Calculate all the numbers if you’re unsure. Choose (C).

17.AThis is really an interest rate problem. The setup is exactly the same except that it’s population growth instead of money growth. r = 3% or 0.03 and t = 5. So the completed formula is 200,000 × (1.03)⁵. Choose (A).

18.CCheck Statement (1). From the group formula, you can set up 250 = 200 + Graduate – Both + 0, but you can’t solve the equation because there are two variables. You can’t answer the question, so narrow your choices to (B), (C), and (E). Try Statement (2). Now you have 250 = Undergraduate + Graduate − 50 + 0, but you still can’t solve the equation. Eliminate (B). Try Statements (1) and (2) together. Now you can fill in 250 = 200 + Graduate − 50 + 0. You can solve for Graduate and answer the question. Choose (C).

19.ASet up a group grid, as shown below, with the given information in bold. If 30 of the 120 advisors work in bonds, the other 90 work in equities. The number of board-certified advisors is 50% × 120 = 60, so the number of noncertified advisors is 120 − 60 = 60. The number of equity advisors that are certified is × 90 = 30, so the number of noncertified equities advisors is 90 − 30 = 60. There are 60 certified advisors and 30 of them work in equities, so 60 − 30 = 30 certified advisors work in bonds. So all 30 bond advisors are certified and none of them are noncertified. Choose (A).

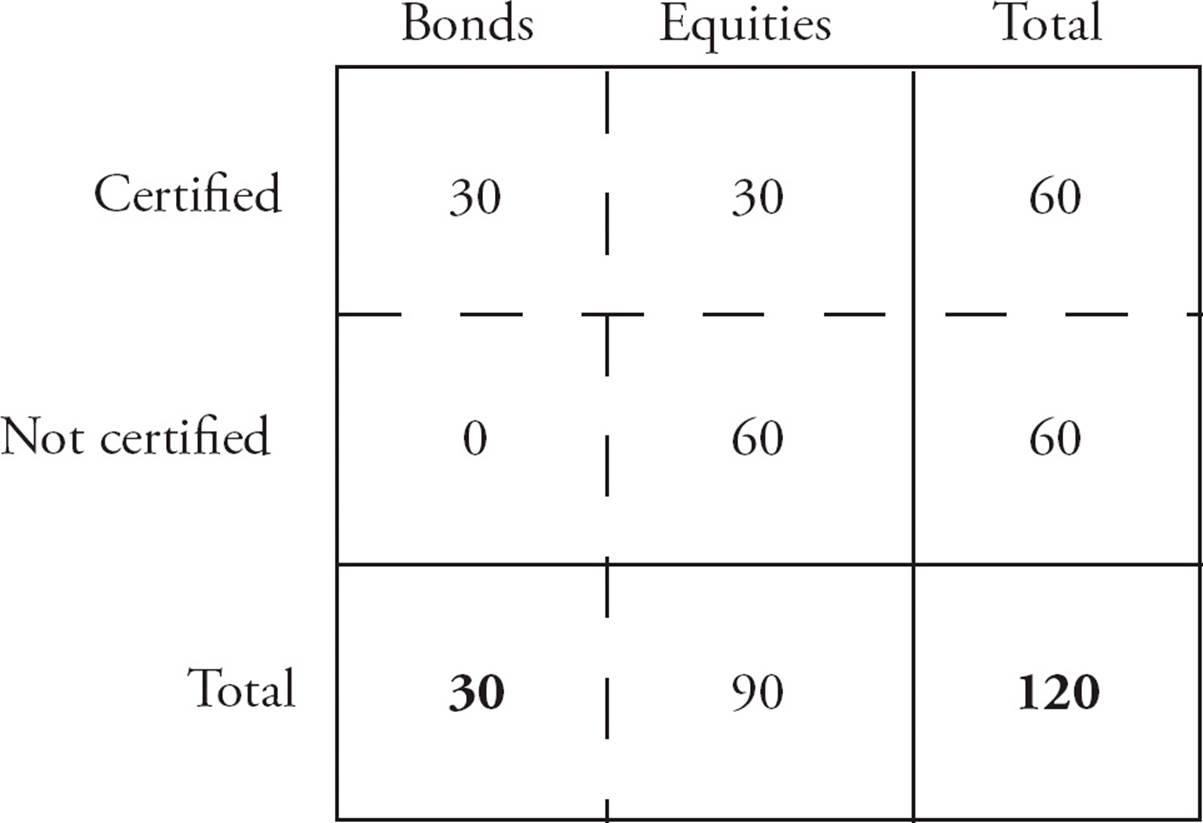
20.CStart with Statement (1). There are three parts to any average: the total, the number of things, and the average. You know the average contribution, but you don’t know the total, so you can’t find the number of things (people). You can’t answer the question. Narrow your choices to (B), (C), and (E). Try Statement (2). Now you know the total contributions, but you don’t know the average. You can’t answer the question, so eliminate (B). Try Statements (1) and (2) together. You know the average and the total, so you can find the number of things. You can answer the question, so choose (C).

21.DStart with Statement (1). If the average of two things is 108, the total is 2 × 108 = 216. Now you can subtract 72 to find the other number. You can answer the question, so eliminate (B), (C), and (E). Try Statement (2). You could set up a ratio box. You have the ratio and one actual number, so you could find all of the actual numbers. You can answer the question, so choose (D).

22.CFirst, try putting the ratios in comparable terms. Multiply the first ratio, 2 to 5, by 4 to get 8 to 20. Multiply the second ratio, 1 to 4, by 5 to get 5 to 20. Now you can see that X has 8 oxygen when Y has 5 oxygen. At this point, you can Plug In The Answers (using a system we call PITA—more on that in the next chapter) on the ratios to see which one works. Start with (C). If the ratio of X to Y is 1 to 2, then for every X, you will add 2 Y. So, one X is 8 oxygen and 20 carbon, while 2 Y is 10 oxygen and 40 carbon. This amounts to 18 oxygen and 60 hydrogen, which reduces to 3 oxygen to 10 hydrogen. This is the correct ratio for the mixture, so choose (C).