Math Workout for the GMAT
Part III Content and Strategy Review
Chapter 7 Geometry
Although you probably studied geometry in high school, the geometry tested on the GMAT is very different. There are no proofs to memorize and regurgitate. However, there are some rules that you need to know and, as always, the GMAT writers will try to trick and confuse you.
The diagrams on problem-solving geometry questions are drawn roughly to scale, unless they say otherwise. This means that an angle that looks significantly bigger than another angle probably is. However, you should know that the computer screen may occasionally distort the diagrams a bit. Don’t assume that an angle that looks like a 90-degree angle really is one. It might be 89 or 91 degrees. Also, straight lines sometimes look jagged on the screen.
The diagram on a data sufficiency question is a different story. Never assume that a data sufficiency diagram is drawn to scale.
Note: A significant number of GMAT questions don’t provide diagrams of the figures described in the questions. Don’t worry; in these cases, the questions supply the information you need to simply draw them yourself.
ANGLES AND LINES
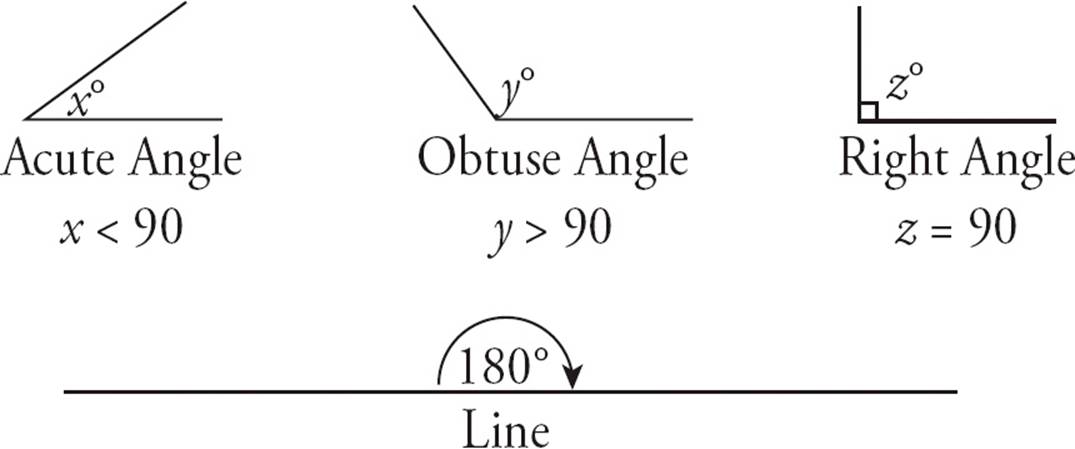
Angles come in three flavors. Acute angles are angles of less than 90 degrees. Obtuse angles are angles of more than 90 degrees. Right angles are angles of exactly 90 degrees. A straight line makes an angle of 180 degrees.
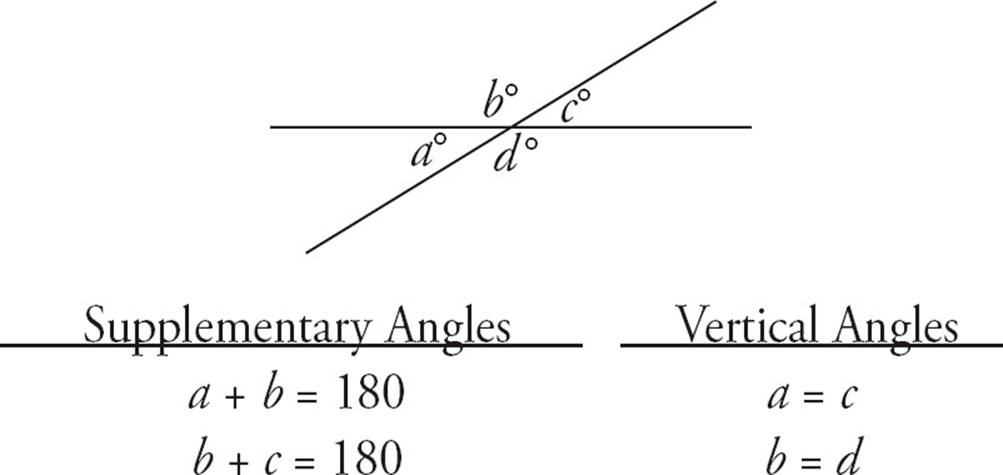
When two lines intersect, they form two kinds of angles. Supplementary angles are angles that combine to form a line. Therefore, they must add up to 180 degrees. Vertical angles are the angles across from each other. They are equal. See the diagram below.
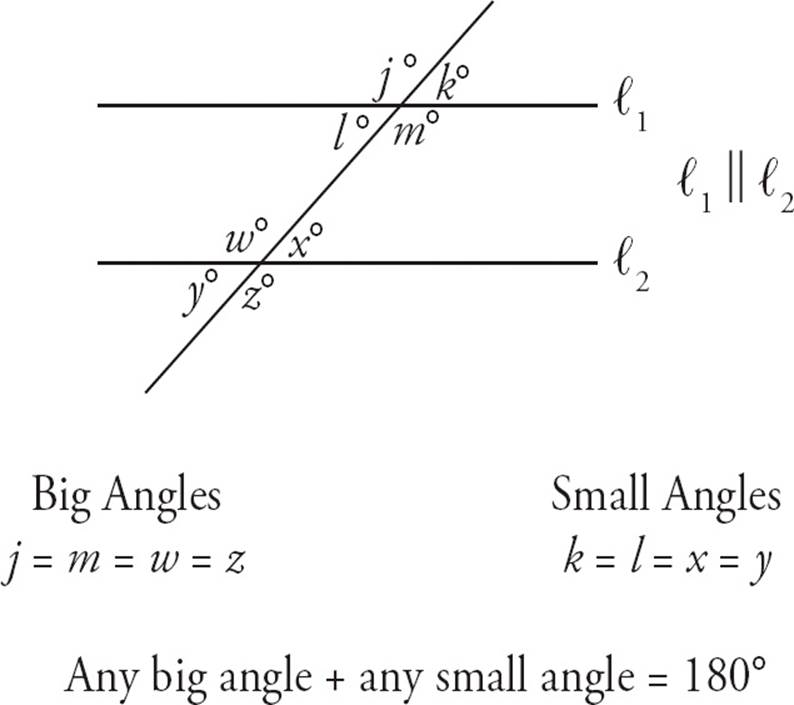
Parallel lines are lines that never intersect. When two parallel lines are intersected by a third line, called a transversal, eight angles are created. However, these angles come in only two sizes. All of the big angles are equal and all of the small angles are equal. See the diagram below.
QUADRILATERALS
The term quadrilateral refers to any four-sided figure. The only important rule that all quadrilaterals follow is that their four inside angles must add up to 360 degrees. There are three specific types of quadrilaterals that do follow other rules: the parallelogram, the rectangle, and the square.
Parallelograms are composed of two sets of parallel lines. Because they involve parallel lines, parallelograms follow the rule about two sizes of angles: The big angles are equal and the small angles are equal. A big angle and a small angle must add up to 180°. Additionally, each side is equal in length to the side opposite it.

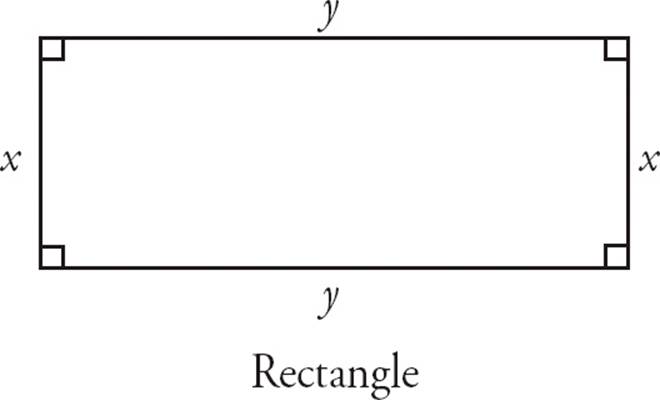
Rectangles are quadrilaterals with four right angles. This also means that their opposite sides are equal. Every rectangle is also a parallelogram.
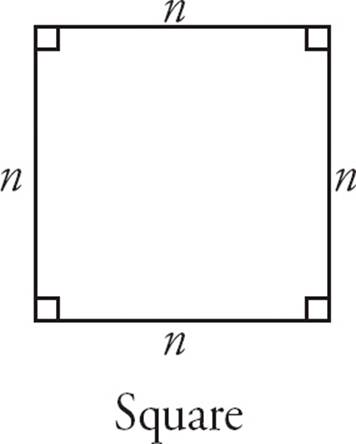
Squares are quadrilaterals that have four right angles and four equal sides. Every square is also a rectangle and a parallelogram.
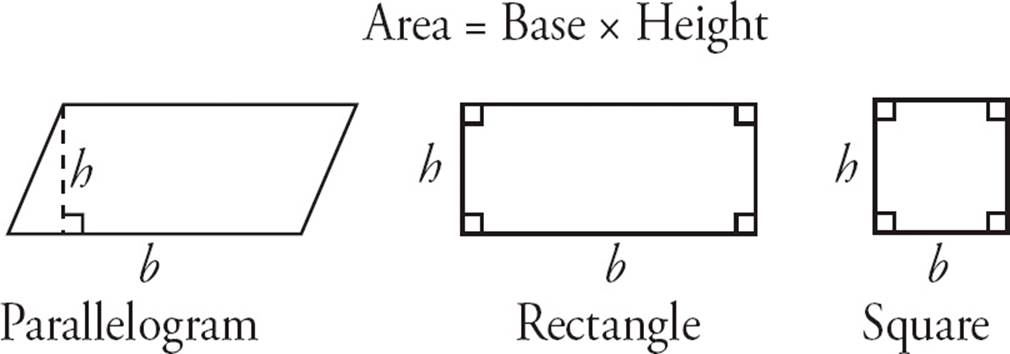
The perimeter of a quadrilateral is simply the sum of all four sides. The area of a parallelogram, rectangle, or square is calculated by the following formula: Area = Base × Height. For rectangles, the area is sometimes expressed as Area = Length × Width. For squares, the area is sometimes expressed as Area = Side2. However, these are just different ways of saying the same thing. The one important thing to remember is that the base and height must be perpendicular (forming a right angle). This is most important with parallelograms, because the sides are not necessarily perpendicular. In that case, the height is a line from the top to the base that forms a right angle to the base. See the diagrams below.
CIRCLES
Circles sometimes intimidate people because they’re curves that you can’t measure with a ruler. However, circles are much easier to handle than you might think. Take a look at the parts of a circle.
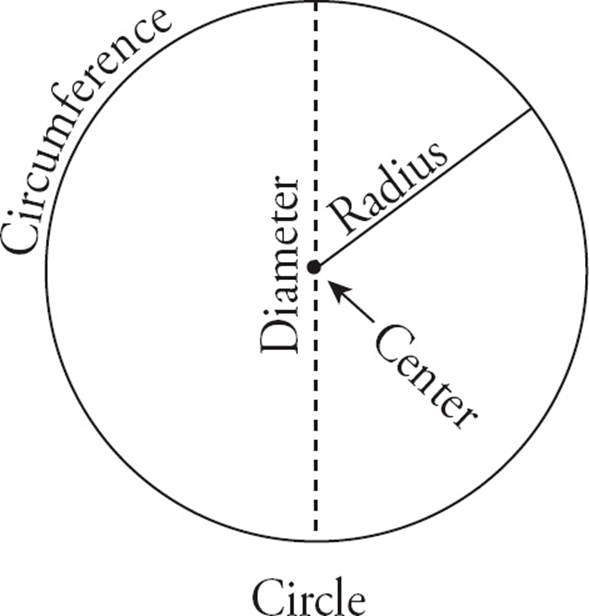
The center is the point at, well, the center of the circle. The circumference of the circle is the distance around the outside of the circle. It’s very much like the perimeter of a quadrilateral or triangle. Each point on the circumference is the same distance from the center of the circle. The distance from the center of the circle to the circumference is the radius. It’s a very important part of the circle because it plays a role in measuring all the other parts of the circle.
A diameter is a line that runs from the edge of the circle, through the center, to the edge on the other side. The diameter is twice the length of the radius, and it is the longest possible distance within a circle. All circles measure 360 degrees.
A chord is a line that runs from one edge of a circle to another. A diameter is a special kind of chord because it runs through the center of a circle. However, not all chords run through the center of the circle.
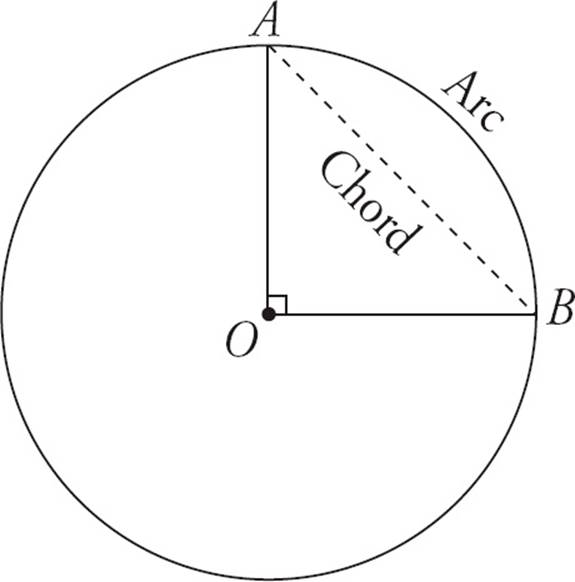
The formula for the area of a circle is Area = πr2, where r is the radius of the circle. π is the symbol for pi, a constant. You don’t need to know the exact value of pi, just that it’s a little more than 3. For example, if the radius of a circle is 3, the area is π(32) = 9π, which is roughly 27. The formula for the circumference of circle is Circumference = 2πr, where r is the radius of the circle. For example, if the radius of a circle is 3, the circumference is (2)(π)(3) = 6π. As you can imagine, finding the radius of the circle is usually the first step in solving a circle problem.
Sometimes a geometry question will ask about a piece of a circle, like a slice of a pie. The rule for these situations is that all the characteristics of the slice are proportional to the size of the slice. For example, if the slice is ![]() of the circle (like AOB in the diagram above), then the area of the slice is
of the circle (like AOB in the diagram above), then the area of the slice is ![]() of the area of the whole circle. The arc of the slice (the piece of the circumference) is
of the area of the whole circle. The arc of the slice (the piece of the circumference) is ![]() of the circumference of the whole circle. The angle of the slice is
of the circumference of the whole circle. The angle of the slice is ![]() of the 360 degrees in a circle, or 90 degrees.
of the 360 degrees in a circle, or 90 degrees.
DRILL 1
Answers can be found on this page.
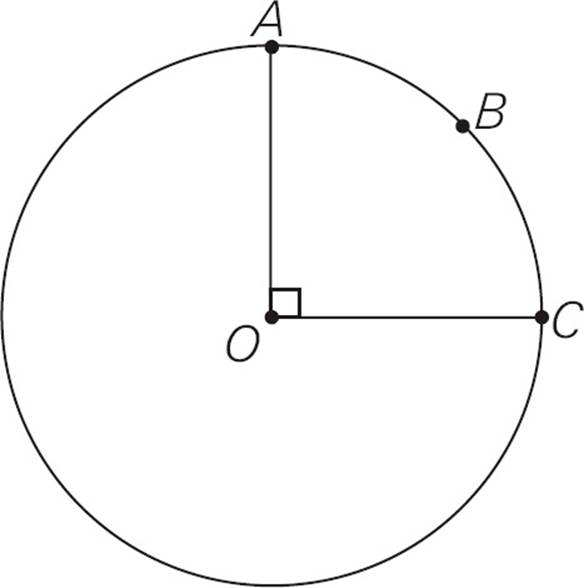
1.If the circle above has center O and an area of 36π, what is the perimeter of sector ABCO ?
|
|
6π |
|
|
9π |
|
|
6 + 3π |
|
|
9 + 3π |
|
|
12 + 3π |
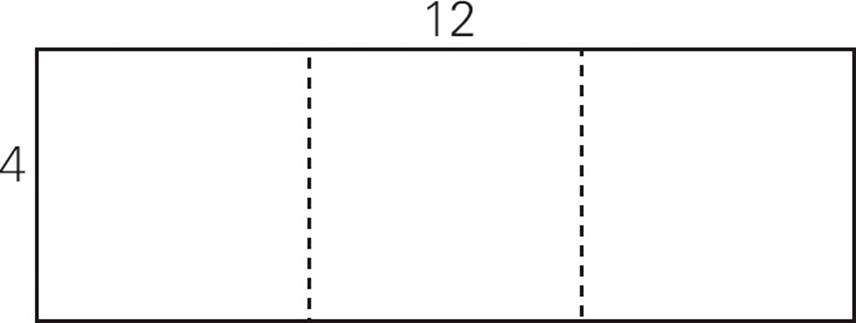
2.If a rectangle measuring 4 inches by 12 inches is cut into 3 equal rectangles, as shown above, what is the perimeter, in inches, of each of the three new rectangles?
|
|
|
|
|
|
|
|
16 |
|
|
24 |
|
|
32 |
TRIANGLES
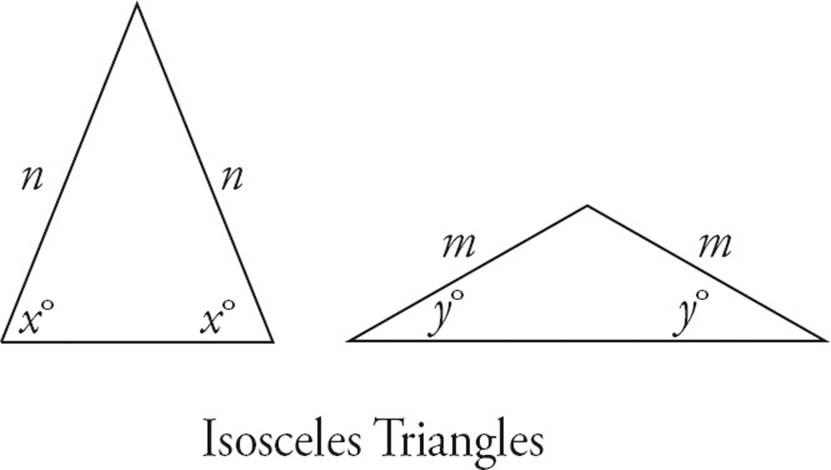
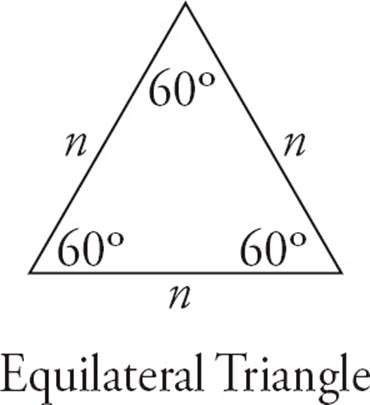
A triangle is any three-sided figure. The three angles in a triangle must add up to 180 degrees. The size of the sides corresponds to the size of the angles. The bigger sides are opposite the bigger angles, and vice versa. There are a couple of special triangles that you should know: isosceles and equilateral.
In an isosceles triangle, two of the sides are equal. Also, the two angles opposite those sides are equal. See the diagrams below.
In an equilateral triangle, all three sides are equal. Also, all three angles are equal. Because there are 180 degrees in a triangle, each angle in an equilateral triangle measures 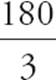 = 60 degrees. See the diagram below.
= 60 degrees. See the diagram below.
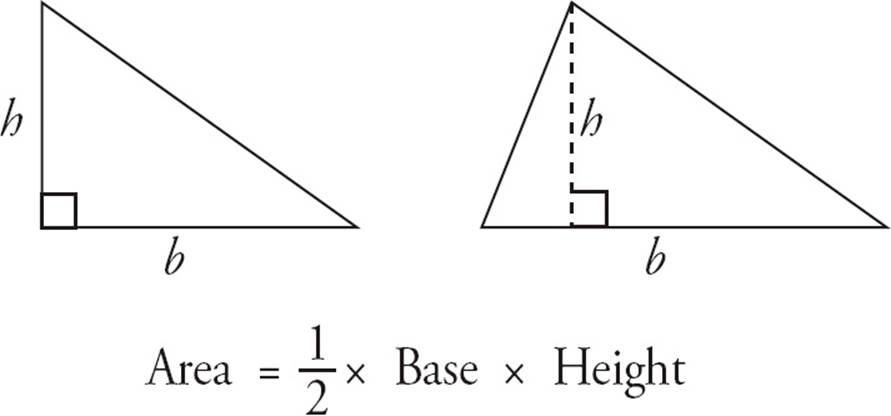
The perimeter of a triangle is simply the sum of the three sides. The area of a triangle is calculated by this formula: Area = ![]() × Base × Height. As with quadrilaterals, the base must be perpendicular to the height. If two sides form a right angle, you can use those sides as the base and height. Otherwise, you’ll have to draw in a line to serve as the height. See the diagrams below.
× Base × Height. As with quadrilaterals, the base must be perpendicular to the height. If two sides form a right angle, you can use those sides as the base and height. Otherwise, you’ll have to draw in a line to serve as the height. See the diagrams below.
Right Triangles
If one of the angles in a triangle is a right angle, that triangle is called a right triangle. The two short sides that form the right angle are called legs, and the longest side (the side opposite the right angle) is called the hypotenuse. The lengths of the sides of a right triangle are related by a formula called the Pythagorean theorem: a2 + b2 = c2, in which a and b are the legs and c is the hypotenuse. If you know the length of two sides, you can use this formula to calculate the length of the third side. Just plug the two known numbers into the appropriate places in the formula and solve for the remaining variable. Remember that the Pythagorean theorem only applies to right triangles.
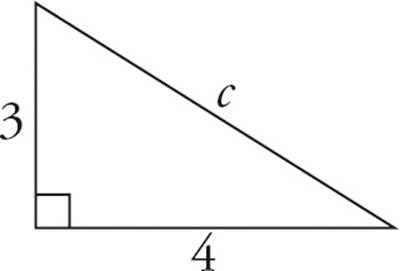
a2 + b2 = c2
32 + 42 = c2
9 + 16 = c2
25 = c2
5 = c
For example, in the figure above, the two known sides are 3 and 4. They go in the a and b spots in the formula because the other side, c, is the hypotenuse. Filled in, the formula now reads 32 + 42 = c2. When you solve the equation, you get c = 5.
The GMAT writers have a couple of favorite versions of the right triangle. They are the 3 : 4 : 5 right triangle and the 5 : 12 : 13 right triangle. These are nothing more than some numbers that happen to work nicely with the Pythagorean theorem to result in integers. They‘re just shortcuts to avoid actually making the calculation with the formula. For example, if you see a right triangle with a side of 3 and a hypotenuse of 5, you can fill in 4 for the other side without needing to do the calculation. If you see a right triangle with sides of 5 and 12 with the hypotenuse missing, you can fill in 13 for the hypotenuse. It’s important to realize that 3 : 4 : 5 and 5 : 12 : 13 are ratios. So a 30 : 40 : 50 triangle works just as well. If you see a right triangle with sides of 10 and 24 with the hypotenuse missing, you can fill in 26 because it’s just a 5 : 12 : 13 right triangle with everything doubled.
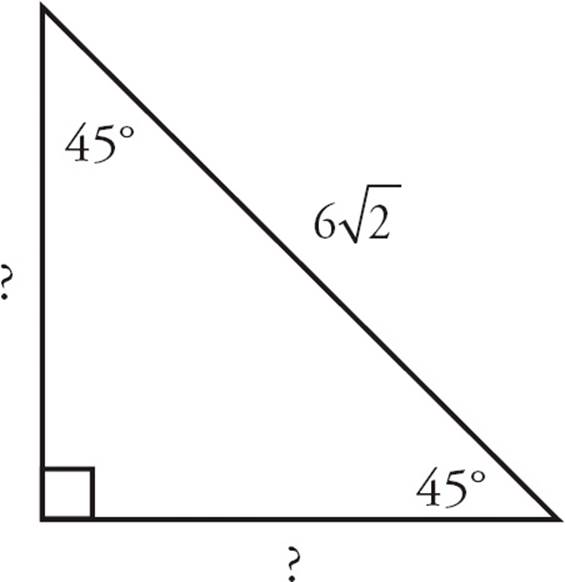
45-45-90 and 30-60-90 Right Triangles
The GMAT frequently tests two other special cases of right triangles: the 45-45-90 and 30-60-90 right triangles. The numbers refer to the angles in each of the triangles. For each of the triangles, the sides follow a certain pattern, or ratio, which you should memorize.
The sides in a 45-45-90 right triangle (also known as an isosceles right triangle) fit the ratio x : x : x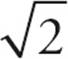 , in which x is the length of each leg. Use the information given to find x; then use that to find the remaining sides.
, in which x is the length of each leg. Use the information given to find x; then use that to find the remaining sides.
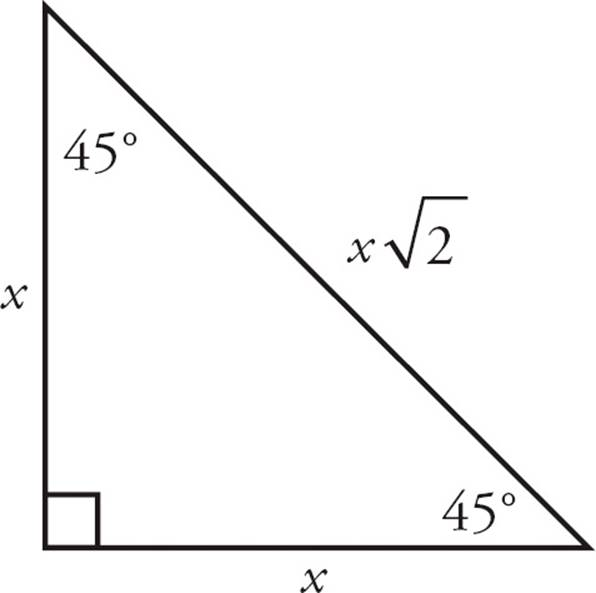
45-45-90 Right Triangle
For example, suppose you’re given an isosceles right triangle with one leg having a length of 3, as shown below. That 3 corresponds to one of the x sides, so x = 3. That means the other two sides are 3 and 3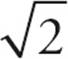 . Just plug in 3 for x on each side.
. Just plug in 3 for x on each side.
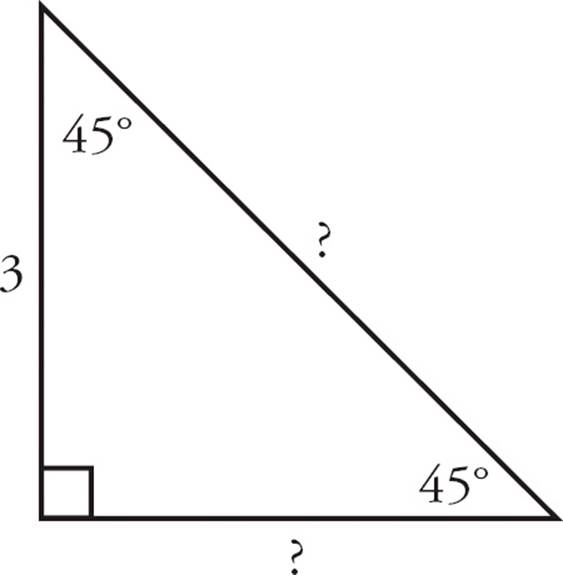
Suppose you know that the hypotenuse of a 45-45-90 triangle is 6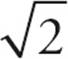 , as shown below. The hypotenuse is the x
, as shown below. The hypotenuse is the x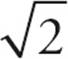 side, so solve the equation x
side, so solve the equation x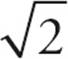 = 6
= 6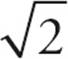 to get x = 6. Then plug 6 in for x on the other sides. Both will be 6.
to get x = 6. Then plug 6 in for x on the other sides. Both will be 6.
The sides of a 30-60-90 right triangle also fit a certain ratio, x : x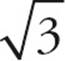 : 2x.
: 2x.
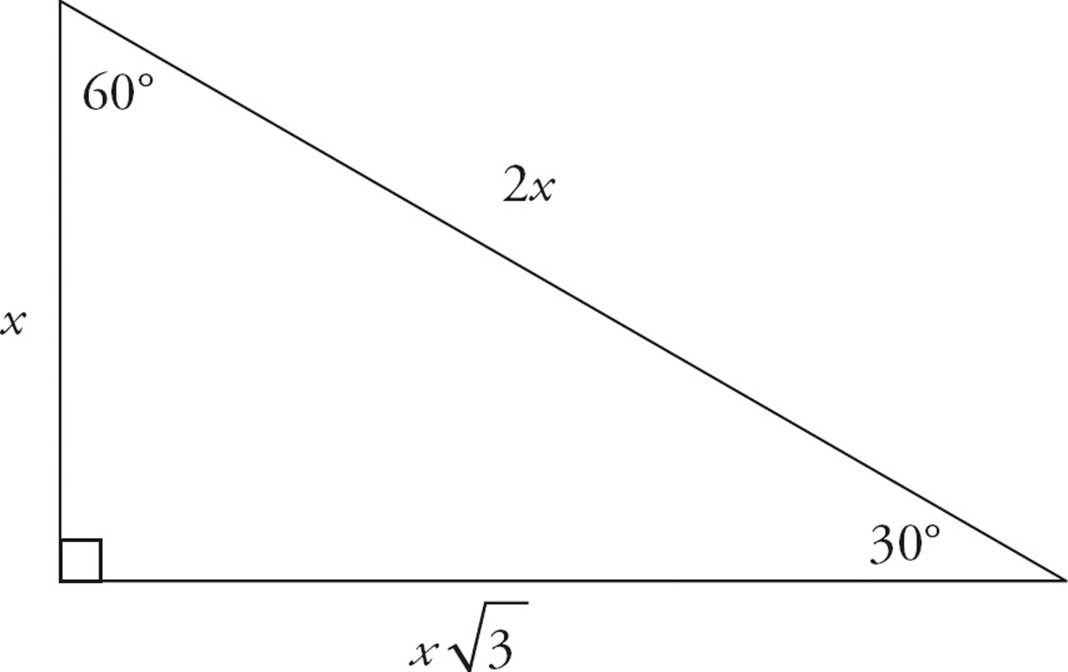
30-60-90 Right Triangle
With this pattern, it’s important to be careful about which side is which. The x, x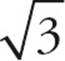 , and 2x lengths correspond to the sides across from the 30°, 60°, and 90° angles, respectively. Remember that the smallest side is across from the smallest angle and the largest side (the hypotenuse) is across from the largest angle. Use the given information to find x, and then plug that into the ratio to find the remaining sides.
, and 2x lengths correspond to the sides across from the 30°, 60°, and 90° angles, respectively. Remember that the smallest side is across from the smallest angle and the largest side (the hypotenuse) is across from the largest angle. Use the given information to find x, and then plug that into the ratio to find the remaining sides.
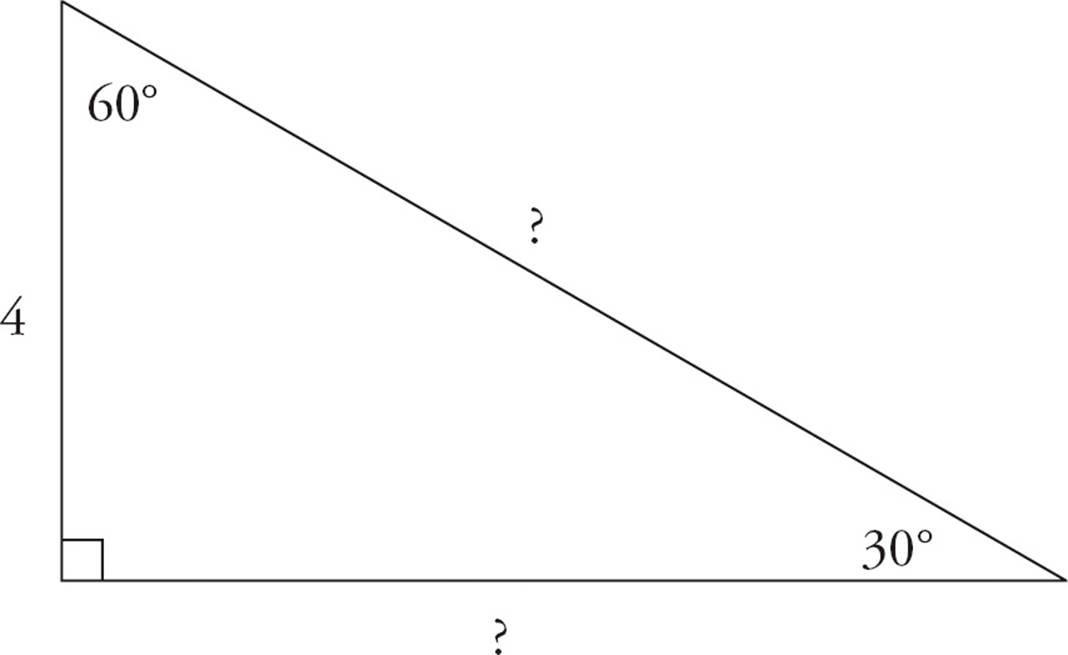
Suppose you’re given a 30-60-90 triangle in which the shortest side has a length of 4, as shown above. The shortest side is the x side, so x = 4. The other leg is x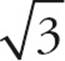 , or 4
, or 4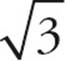 , and the hypotenuse is 2x, or 8.
, and the hypotenuse is 2x, or 8.
Do you need these patterns if you know the Pythagorean theorem? Yes. With the standard Pythagorean theorem, you need to know two sides to find the third. With the special ratios, you need only one side to find the others, provided the angles fit the patterns. Also, you can use the sides to find the angles in some cases. For example, if you see a triangle with sides of length 5, 5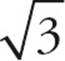 , and 10, then it must be a 30-60-90 triangle.
, and 10, then it must be a 30-60-90 triangle.
The Third Side Rule
Some GMAT questions will tell you the lengths of two sides of a triangle and ask you about the length of the third. If the triangle is a right triangle, you simply apply the Pythagorean theorem or one of the special right triangle patterns. However, these apply only to right triangles. With a non-right triangle, you cannot find the exact length of the third side using only the lengths of the other two sides, but you can determine a range for its length by using the third side rule.
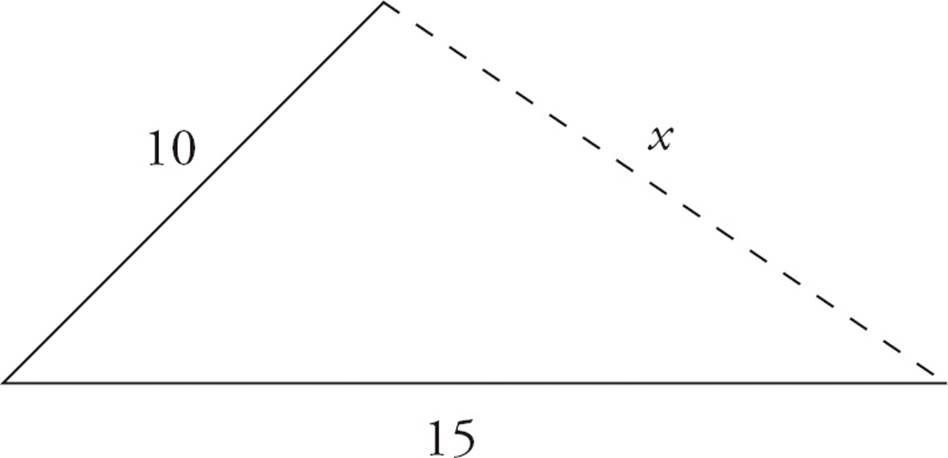
The third side rule says that the length of an unknown side of a triangle must be less than the sum of the two known sides but more than their difference. In the figure above, that means (15 − 10) < x < (15 + 10), so the missing side is between 5 and 25.
Pretend that the known sides are connected by a hinge, so that they can be opened and closed like the cover of a book. The unknown side is a rubber band that expands and contracts as the known sides are opened and closed. If the known sides are fully opened so that they form a 180° angle, the unknown side will be as long as both of the known sides put together. However, that’s not a triangle. To make a triangle, you must close the known sides just a bit, making the unknown side a little less than the sum of the known sides.
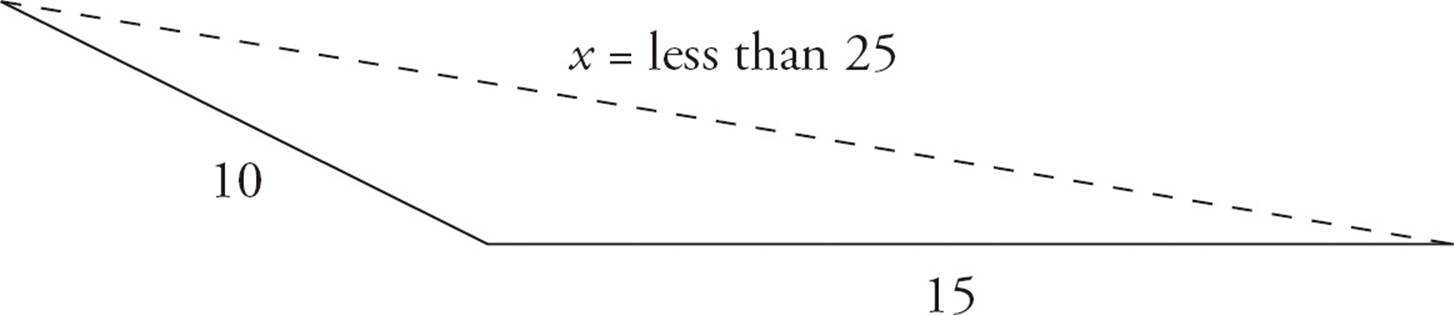
Now, completely close the known sides so that they overlap. The unknown side is the distance between their ends, or the difference in their lengths. Again, this isn’t a triangle; you must open the known sides slightly. Now, the length of the unknown side is a bit more than the difference in length of the known sides.

The third side rule doesn’t provide an exact number for the length of the unknown side, but it does put limits on the possible length. Tough data sufficiency questions often test this idea.
DRILL 2
Answers can be found on this page.
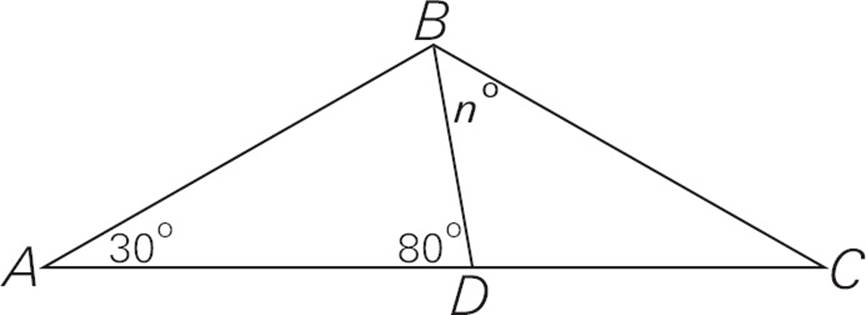
1.In the figure above, if AB = BC, then n =
|
|
30° |
|
|
40° |
|
|
50° |
|
|
60° |
|
|
70° |
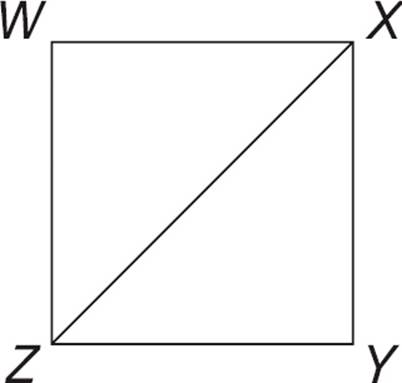
2.If square WXYZ above has an area of 100, what is the length of diagonal XZ ?
|
|
10 |
|
|
10 |
|
|
10 |
|
|
100 |
|
|
100 |
OVERLAPPING FIGURES
Many geometry problems on the GMAT involve more than one geometric shape. For example, you might see a circle drawn inside a square. The key to solving these problems is to find the link between the two figures. You can see this in the following example.
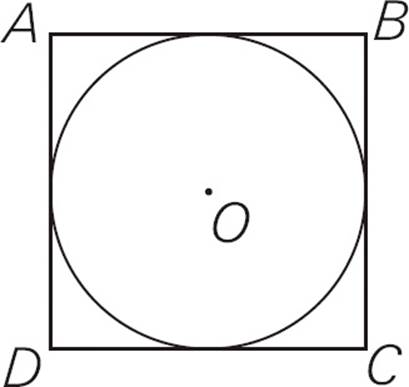
1.In the figure above, the circle with center O has an area of 25π. What is the area of square ABCD ?
|
|
5 |
|
|
10 |
|
|
25 |
|
|
50 |
|
|
100 |
If the circle has an area of 25π, you can determine that the radius is 5, which makes the diameter 10. The link between the two shapes is that the diameter of the circle equals the side of the square. Try drawing a vertical diameter for the circle and seeing how it matches the vertical side of the square. So the side of the square is 10, which means that the area of the square is 10 × 10 = 100. The correct answer is (E).
Shaded Regions
Some geometry problems deal with the area of a shaded region. Instead of treating the shaded region as a separate shape and trying to calculate its area directly, you should treat it as something formed by two overlapping shapes. Typically, its area is the remainder when you subtract the area of a smaller shape from that of a larger shape.
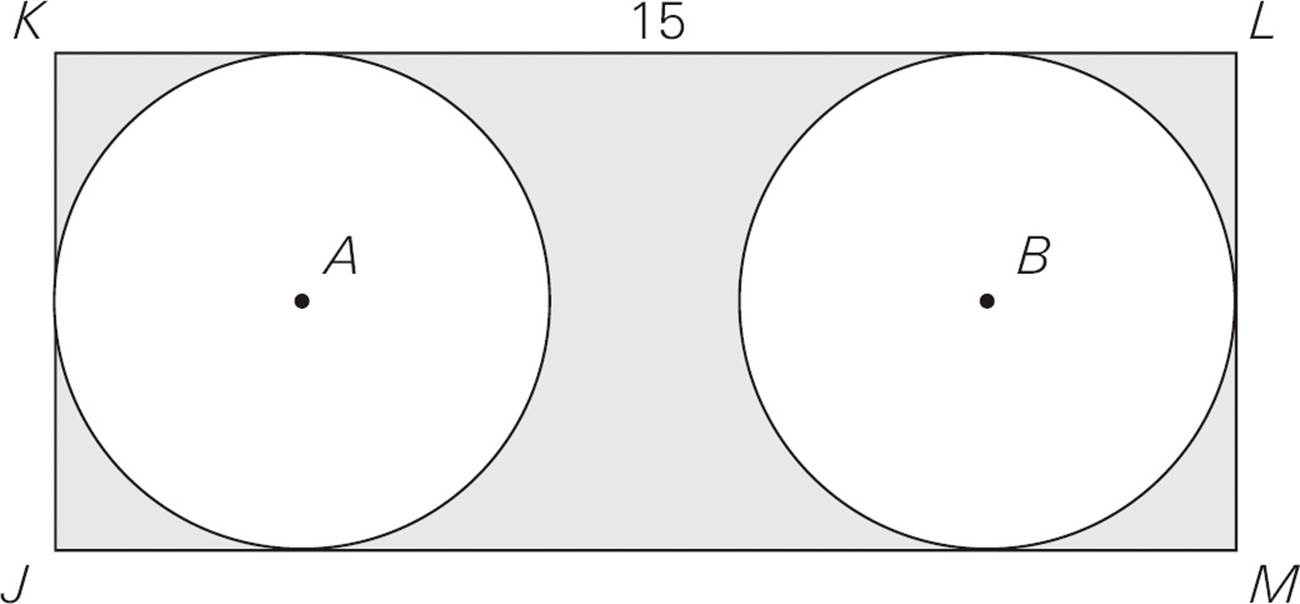
2.In the figure above, circles with centers A and B are inscribed in rectangle JKLM. If the area of JKLM is 90, what is the area of the shaded region?
|
|
90 − 9π |
|
|
90 − 15π |
|
|
90 − 18π |
|
|
90 − 36π |
|
|
90 − 72π |
The shaded region is formed by subtracting the two circles from the rectangle. Plug the rectangle’s area, 90, and its length, 15, into the area formula: A = l × w, or 90 = 15 × w. Solving, you find the width is w = 6. The radius of each circle is half of the rectangle’s width, or 3. Plug that into the area formula for a circle: A = πr2 = π32 = 9π. The area of the shaded region is the area of the rectangle minus the area of the two circles: 90 − 9π − 9π or 90 − 18π. The correct answer is (C).
SOLIDS
Solids are three-dimensional geometric shapes, including cubes, cylinders, spheres, and so on. You may be asked to find the volume or the surface area of a solid.
Volume
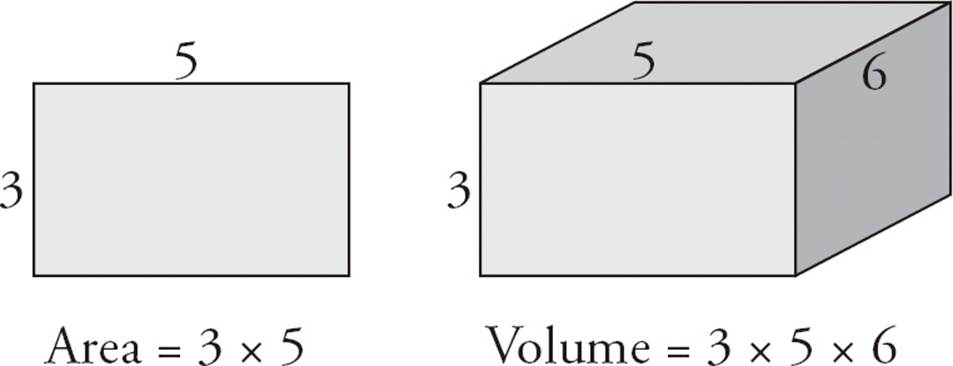
Finding the volume of a solid is very similar to finding the area of a shape. In fact, if you think of a solid as a flat shape times one more dimension, that’s how you find the volume. Just multiply the area by the extra number, which is the third dimension.
Suppose you have a rectangle with measurements of 3 by 5. The area is 3 × 5 = 15. If you have a rectangular solid with measurements of 3 by 5 by 6, the volume is 3 × 5 × 6. A cube is just a rectangular solid with the same measurement in all three dimensions.
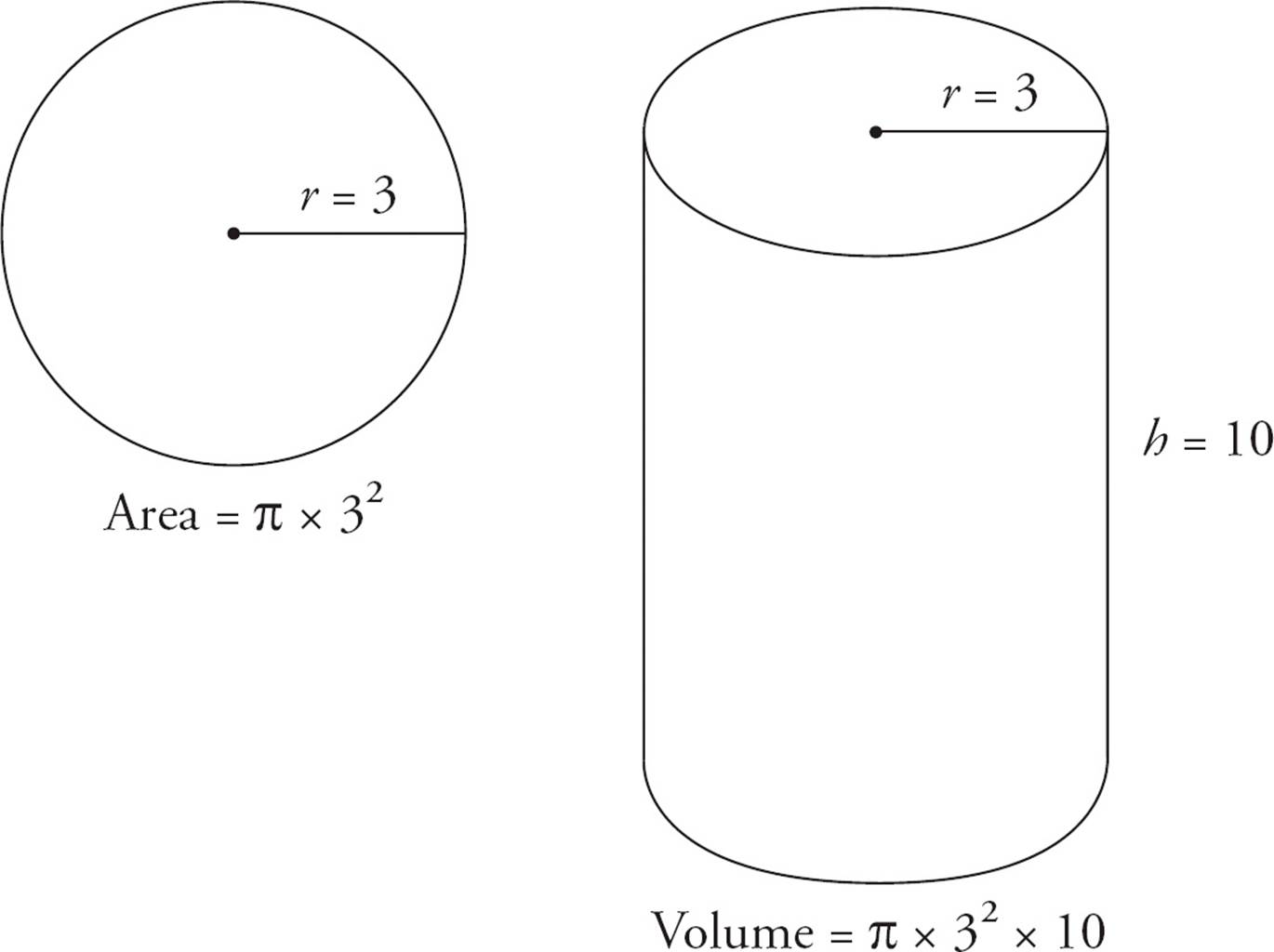
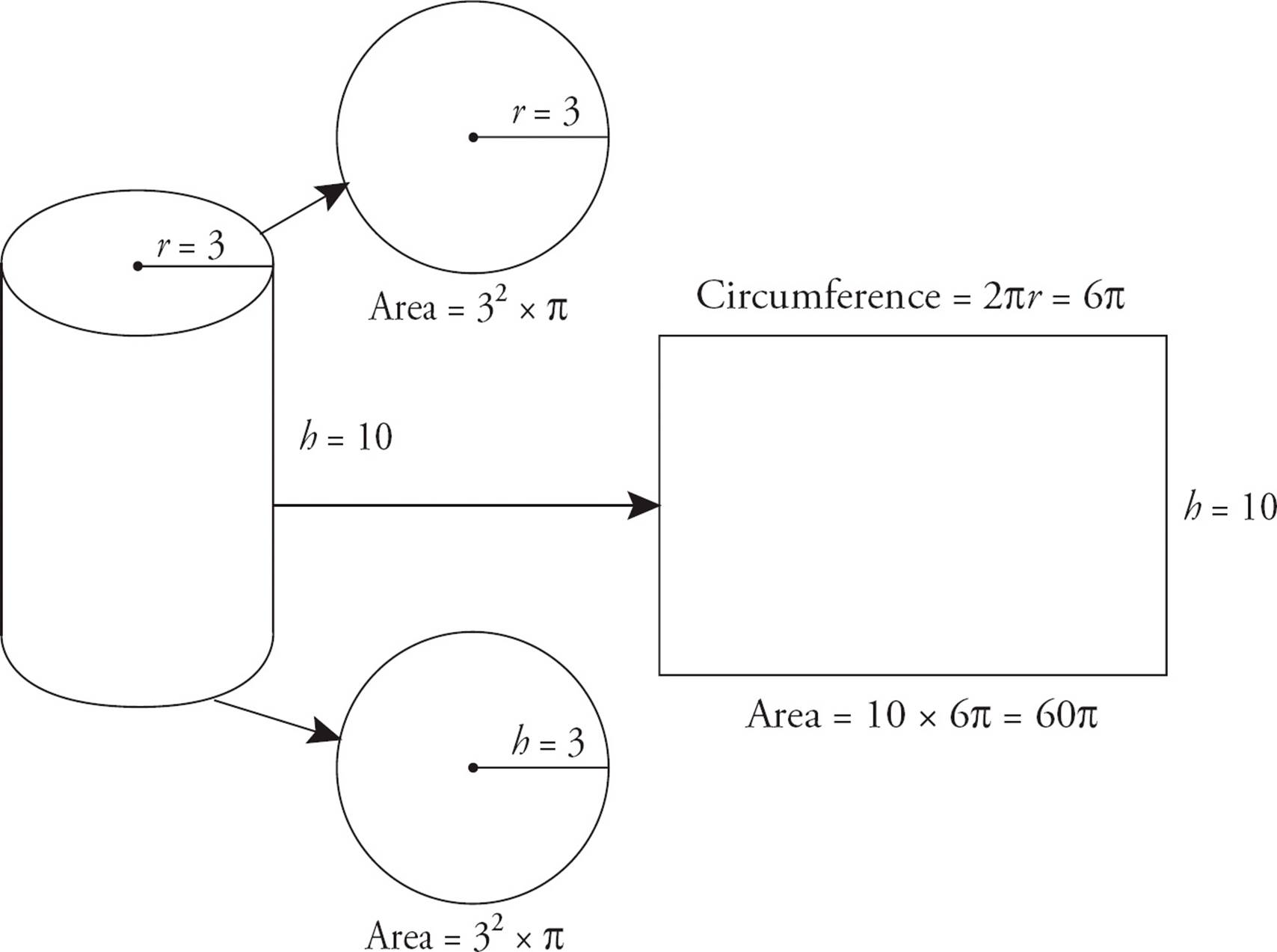
The volume of a cylinder follows a similar pattern. Start with the area of a circle. Then, multiply by the height of the cylinder. Officially, the formula is V = π × r2 × h, but that’s just the area of the circle times h. In the cylinder shown below, the area of the circle is πr2 = π × 32 = 9π. To find the volume of the cylinder, multiply that area by the height of the cylinder: 9π ×10 = 90π. For any other solid, such as a sphere, the question will provide the formula.
Surface Area
To calculate the surface area of a solid, break it up into several flat figures and find the area of each. For example, the 3 by 5 by 6 rectangular solid mentioned earlier has six faces: two are 3 by 5, two are 3 by 6, and two are 5 by 6. So the total surface area is (3 × 5) + (3 × 5) + (3 × 6) + (3 × 6) + (5 × 6) + (5 × 6) = 15 + 15 + 18 + 18 + 30 + 30 = 126.
The cylinder discussed earlier has two circular surfaces, the top and the bottom. Each circle has an area of 32 × π = 9π. When you “unroll” the vertical part of the cylinder, you get a rectangle, as shown below. (Think of unwrapping a paper towel from the roll.) The top edge of the rectangle is equal to the circumference of the circle: 2πr = 2 × π × 3 = 6π. The vertical edge of the rectangle is the height of the cylinder: h = 10. Thus, the area of the rectangle is 6π × 10 = 60π, and the total surface area of the cylinder is 9π + 9π + 60π = 78π.
Distance
Occasionally, the GMAT will test you on the distance between two points in a three-dimensional space. This often takes the form of a diagonal line between opposite corners of a rectangular box. The formula for this is sometimes called the Super Pythagorean formula, because it is closely related to the formula for right triangles.
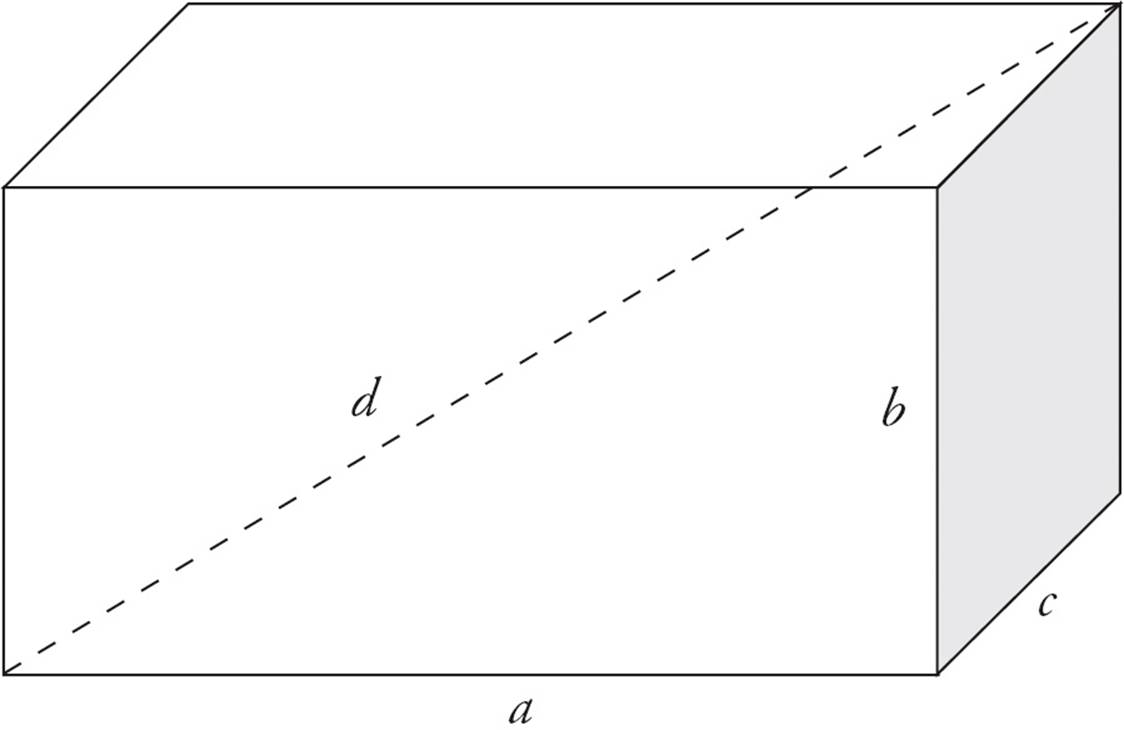
a2 + b2 + c2 = d2
The length of the diagonal line is d, and the dimensions of the box are a, b, and c. Note that it doesn’t matter which dimension is called a, b, or c. Plug in the numbers for a, b, and c, and then solve for d.
1.A cube has a volume of 125 cubic inches. What is the length, in inches, of the longest line that can be drawn between any two points on the cube?
|
|
5 |
|
|
5 |
|
|
5 |
|
|
5.5 |
|
|
5 |
Start by drawing a picture of a cube. The formula for the volume of a cube is V = s3, so 125 = s3, or s = 5. The longest possible line will be a diagonal between two opposite corners. That’s the d in the Super Pythagorean formula. The dimensions of a cube are all equal, so plug 5 in for a, b, and c to get 52 + 52 + 52 = d2 or 25 + 25 + 25 = d2. Since d2 = 75, then d = 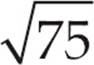 =
=  ×
× 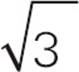 = 5
= 5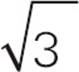 . So answer choice (B) is correct.
. So answer choice (B) is correct.
COORDINATE GEOMETRY
The coordinate grid is made up of an x-axis and a y-axis. When a coordinate is listed, it will be in the format of (x,y). The x number indicates the position on the x-axis and the y indicates the position on the y-axis. It’s very easy to get your x and y confused. Be careful, because those reversed answers will usually be there to trap you. The following diagram demonstrates the coordinate grid and the position of a point.
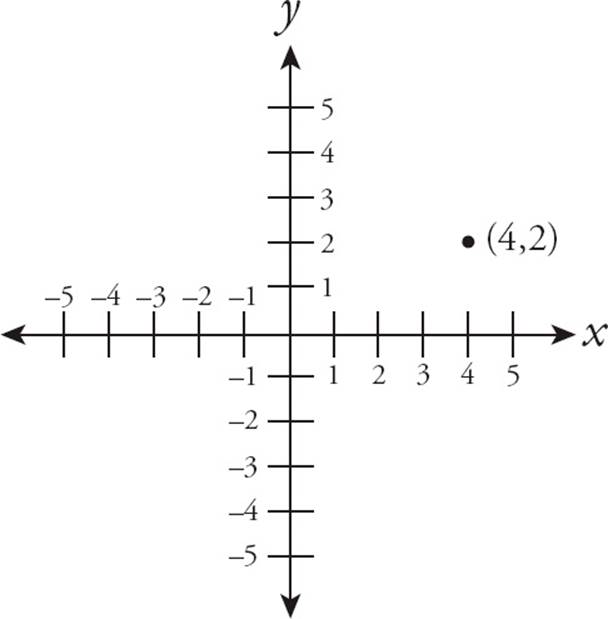
Some geometry questions provide a line on a coordinate grid and ask you to determine its length. This is really just a triangle question in disguise. To solve a problem like this, draw a right triangle, making the line in question the hypotenuse. Make each of the other sides parallel to either thex-axis or the y-axis. Look at the example below.
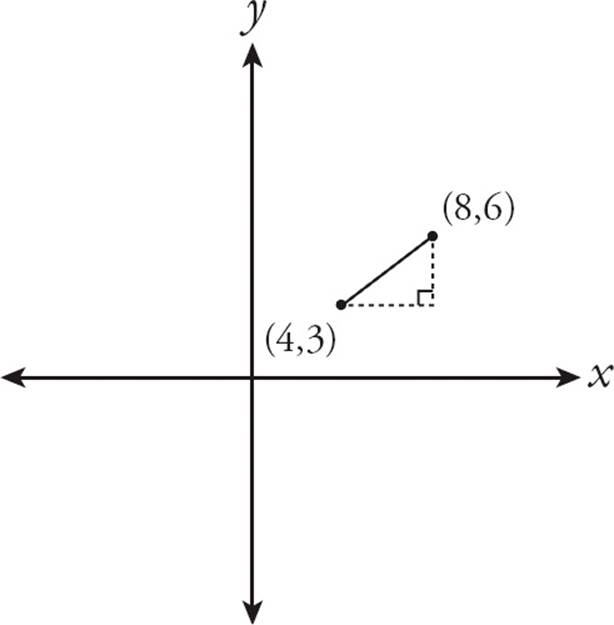
The horizontal side goes from x = 4 to x = 8, so its length is 4. The vertical side goes from y = 3 to y = 6, so its length is 3. Once you know these two values, you can use the Pythagorean theorem to find the length of the third side. In this case, it’s the hypotenuse of a 3 : 4 : 5 right triangle, so the length is 5.
Slope
Some questions may ask you to find the slope (m) of a line. The easy definition of slope is “rise over run” or 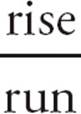 . Rise is the change in the value of y between two points on the line, and run is the change in x. Thus, the slope formula is
. Rise is the change in the value of y between two points on the line, and run is the change in x. Thus, the slope formula is 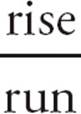 =
= 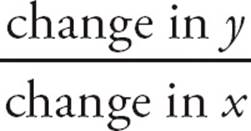 =
= 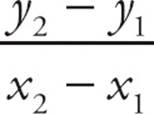 . Just find two points on the line, subtract one y from the other, and put the result in the numerator of the fraction. Then subtract one x from the other and put that in the denominator of the fraction. Make sure you start with the same point for both subtractions. Otherwise, the positive/negative sign of your answer will be wrong.
. Just find two points on the line, subtract one y from the other, and put the result in the numerator of the fraction. Then subtract one x from the other and put that in the denominator of the fraction. Make sure you start with the same point for both subtractions. Otherwise, the positive/negative sign of your answer will be wrong.
Here’s an example.
1.If the points (5,7) and (8,13) are on a line, what is the slope of that line?
|
|
−2 |
|
|
− |
|
|
|
|
|
2 |
|
|
8 |
To find the slope, substitute the known values in the slope formula:
m = 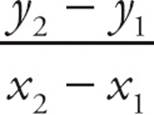 =
= 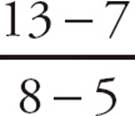 =
= ![]() = 2
= 2
The slope of the line is 2, which means that the line goes up two units for every one unit it goes to the right. The answer is (D).
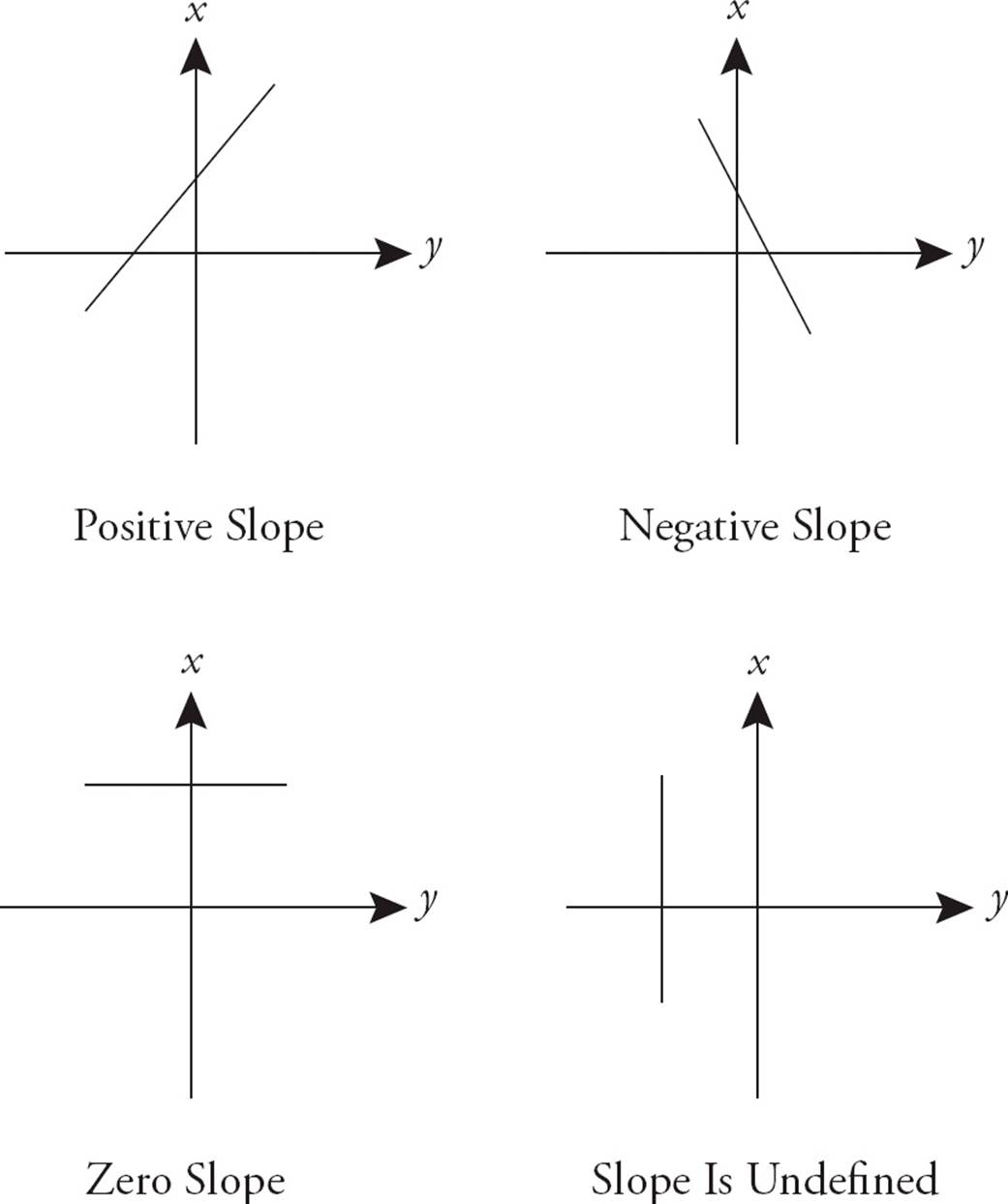
A line with a positive slope goes up to the right. A line with a negative slope goes down to the right. A horizontal line has a slope of 0 (rise is 0), and a vertical line’s slope is undefined (0 in the denominator). The diagrams below illustrate each of these conditions.
Line Equation
y = mx + b
m is the slope of the line
b is the y-intercept of the line
The equation of a line is usually expressed in the slope-intercept form y = mx + b, in which m and b are particular numbers defining the line. The m is the slope of the line, which you just learned to calculate. The b is called the y-intercept, and the line crosses the y-axis at the point (0,b). For example, the line y = −2x + 3 has a slope of −2 (that is, it goes down two units for every one unit to the right) and crosses the y-axis at the point (0,3). The line y = ![]() x − 4 has a slope of
x − 4 has a slope of ![]() (i.e., goes up two units for every three units to the right) and crosses the y-axis at (0,−4). If the equation for a line is not in y = mx + b format, you simply need to solve the equation for y, moving all coefficients and constants to the right side of the equation.
(i.e., goes up two units for every three units to the right) and crosses the y-axis at (0,−4). If the equation for a line is not in y = mx + b format, you simply need to solve the equation for y, moving all coefficients and constants to the right side of the equation.
2.What is the slope of the line defined by the equation 2x − 3y = 9 ?
|
|
−2 |
|
|
– |
|
|
|
|
|
|
|
|
2 |
The equation is not in y = mx + b format, so you need to get y by itself on the left side. First, subtract 2x from each side to get −3y = −2x + 9. Then, divide everything by −3 to get y = ![]() x − 3. The slope is the number in front of x, which is
x − 3. The slope is the number in front of x, which is ![]() . The correct answer is (C).
. The correct answer is (C).
Every point on the line must fit the equation for that line. That means you could plug the x- and y-coordinates into the equation and everything will fit. For example, the point (2,5) is on the line y = x + 3 because 5 = 2 + 3. Try this example.
3.Which of the following points is the intersection between the lines y = 3x + 6 and y = −2x − 4 ?
|
|
(2,0) |
|
|
(0,−2) |
|
|
(−2,0) |
|
|
(0,2) |
|
|
(1,5) |
To be the intersection of the lines, the correct answer must fit both equations. The easiest way to check this is to plug the coordinates into each equation to see whether they fit. Plugging (A) into the first equation, you get 0 = 3(2) + 6, or 0 = 12. That won’t work. You don’t even need to check the second equation. Plugging (B) into the first equation, you get −2 = 3(0) + 6, or −2 = 6. That won’t work. Plugging (C) into the first equation, you get 0 = 3(−2) + 6, which simplifies to 0 = −6 + 6, or 0 = 0. That works. Try that point in the second equation. You get 0 = −2(−2) − 4, or 0 = 4 − 4. That also works. (C) fits both equations, so it must be the right answer.
DRILL 3
Answers can be found on this page.
1.A cylinder of wax is 20 inches tall with a radius of 1 inch. If this cylinder is melted and poured into a new cylindrical mold with a radius of 2 inches, what will be the height of the new cylinder in inches?
|
|
5 |
|
|
10 |
|
|
15 |
|
|
20 |
|
|
40 |
2.A line that passes through the point (2,5) has a slope of −![]() . Which of the following points is not on the line?
. Which of the following points is not on the line?
|
|
(11,−1) |
|
|
(8,1) |
|
|
(4,7) |
|
|
(−1,7) |
|
|
(5,3) |
Comprehensive Geometry Drill
Answers can be found on this page.
Remember!
For Data Sufficiency problems in this book, we do not supply the answer choices. The five possible answer choices are the same every time.
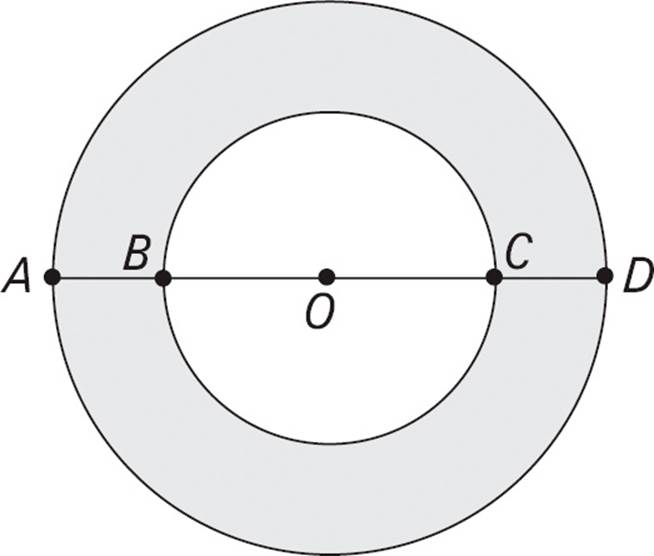
Note: Figure not drawn to scale.
1.The figure above contains two circles with center O. If OD = 10 and the area of the shaded region is 36π, what is the area of the smaller circle?
|
|
6π |
|
|
10π |
|
|
36π |
|
|
64π |
|
|
100π |
2.If the length of a rectangle is decreased by 10% and its width is decreased by 20%, by what percent does its area decrease?
|
|
30% |
|
|
28% |
|
|
25% |
|
|
23% |
|
|
15% |
3.Freddy has a piece of string that is 20 inches long. He wants to use the string as the perimeter of a rectangle. What is the greatest area that rectangle could have?
|
|
5 |
|
|
10 |
|
|
20 |
|
|
25 |
|
|
40 |
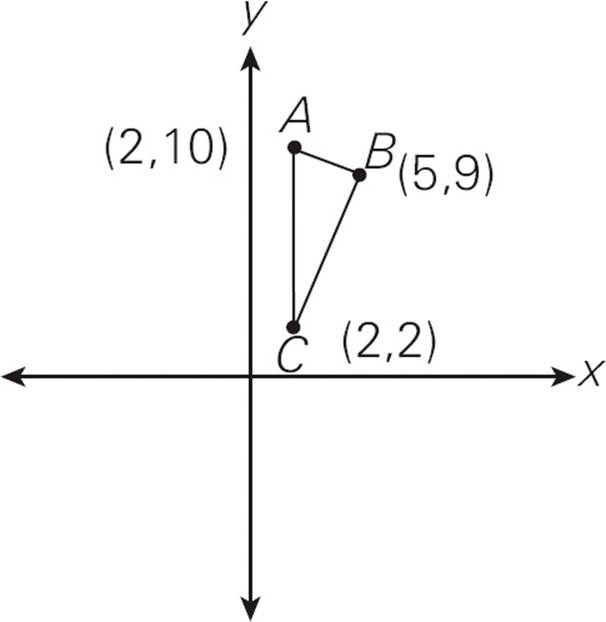
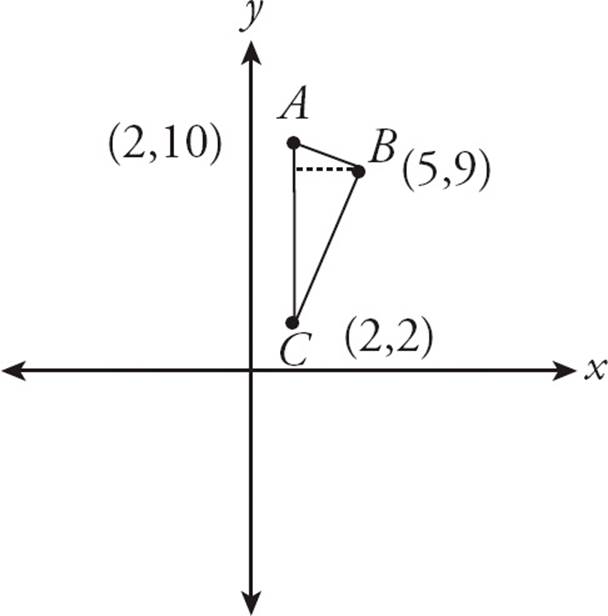
4.In the coordinate system above, what is the area of triangle ABC ?
|
|
10 |
|
|
12 |
|
|
24 |
|
|
25 |
|
|
50 |
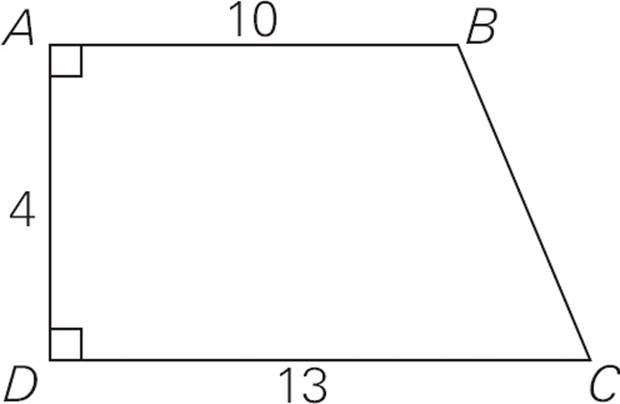
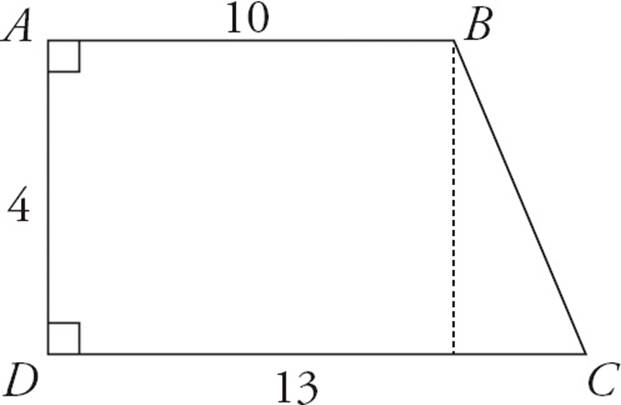
5.What is the area of quadrilateral ABCD above?
|
|
52 |
|
|
46 |
|
|
40 |
|
|
26 |
|
|
20 |
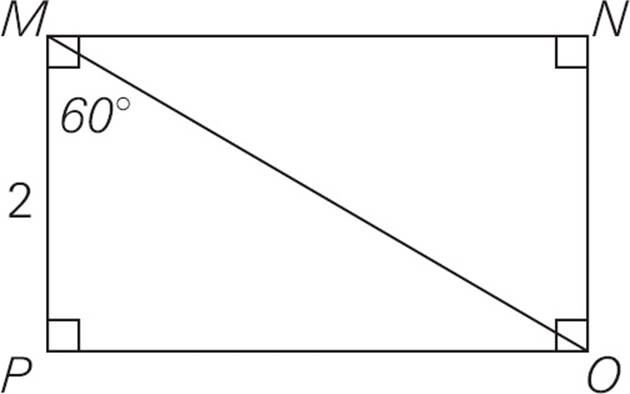
6.In rectangle MNOP above, if MP = 2, what is the length of MO ?
|
|
2 |
|
|
2 |
|
|
4 |
|
|
5 |
|
|
6 |
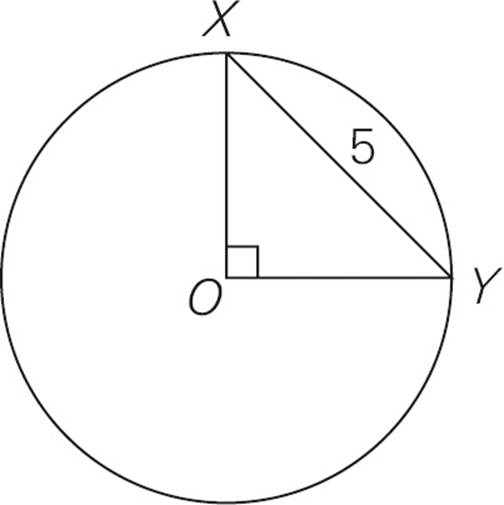
7.In the figure above, if XY = 5, what is the area of the circle with center O ?
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
25π |
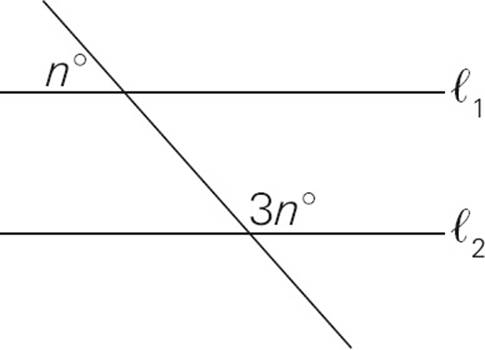
8.If ℓ1 is parallel to ℓ2 in the figure above, what is the value of n ?
|
|
30 |
|
|
45 |
|
|
60 |
|
|
105 |
|
|
135 |
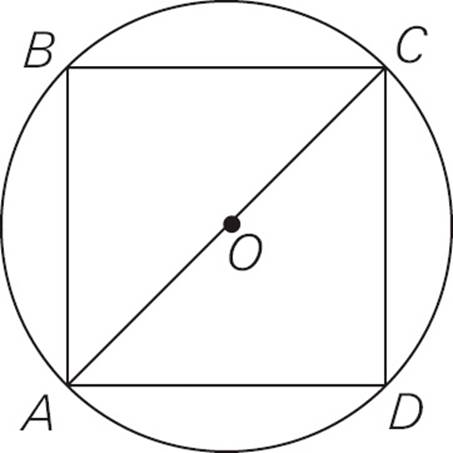
9.In the figure above, square ABCD has an area of 25. What is the area of the circle with center O ?
|
|
|
|
|
|
|
|
|
|
|
25π |
|
|
25 |
10.The hypotenuse of an isosceles right triangle has a length of h, and the triangle has an area of a. Which of the following must be true?
|
|
a = 4h2 |
|
|
a = 2h2 |
|
|
a = h2 |
|
|
4a = h2 |
|
|
2a = h2 |
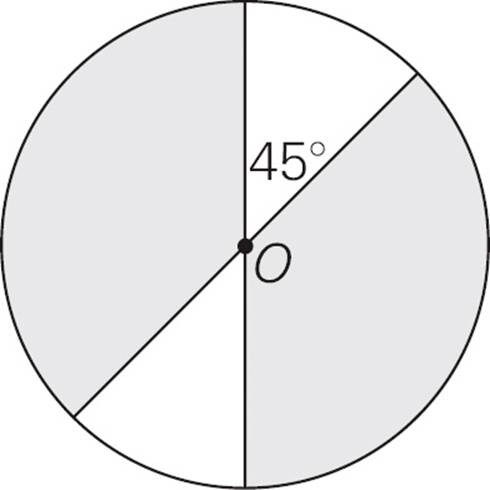
11.In the figure above, what fraction of the circle with center O is shaded?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12.A cylinder has a volume of 180π cubic inches and the radius of its circular base is 6 inches. What is the length of the longest line segment that can be drawn from one point on the cylinder to another?
|
|
|
|
|
12 |
|
|
13 |
|
|
5π |
|
|
6π |
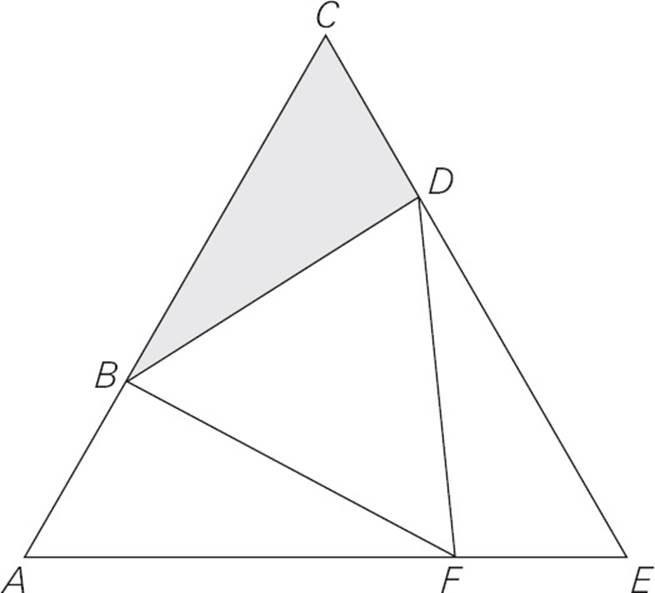
13.Equilateral triangle BDF is inscribed in equilateral triangle ACE, as shown in the figure above. The shaded region is what fraction of the area of triangle ACE ?
(1) ∠DFE = 90°
(2) The length of AF is 10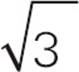 .
.
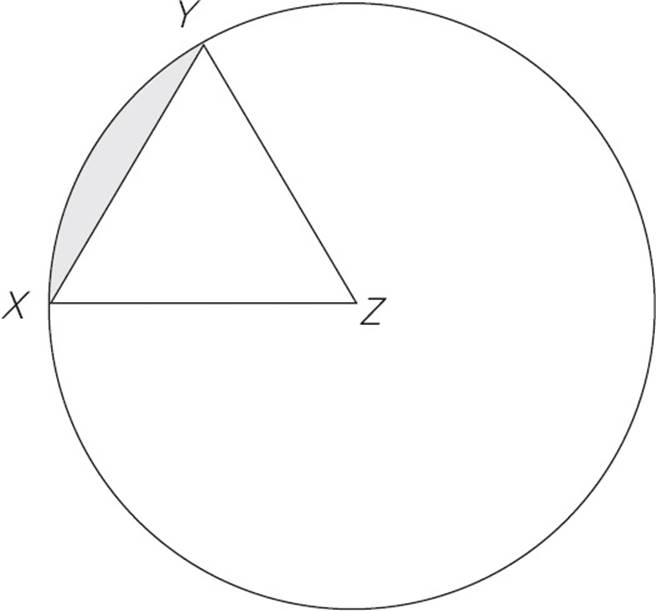
14.In the figure above, triangle XYZ is equilateral and has an area of 9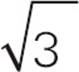 . Points X and Y are on the circle with center Z. What is the area of the shaded region?
. Points X and Y are on the circle with center Z. What is the area of the shaded region?
|
|
6π − 9 |
|
|
12π − 9 |
|
|
(9 |
|
|
9 |
|
|
36π − 9 |
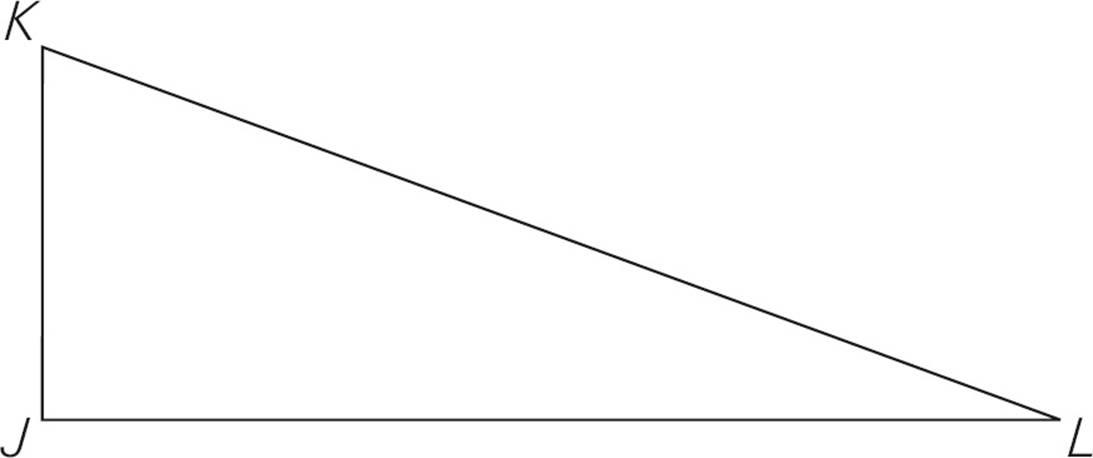
15.In the figure above, JKL is a right triangle. What is the area of triangle JKL ?
(1) The length of JK is 3.
(2) The length of KL is 6.
16.What is the slope of line m ?
(1) The points (1,5) and (5,−7) lie on line m.
(2) Line m is parallel to the line described by 3x + y = 17.
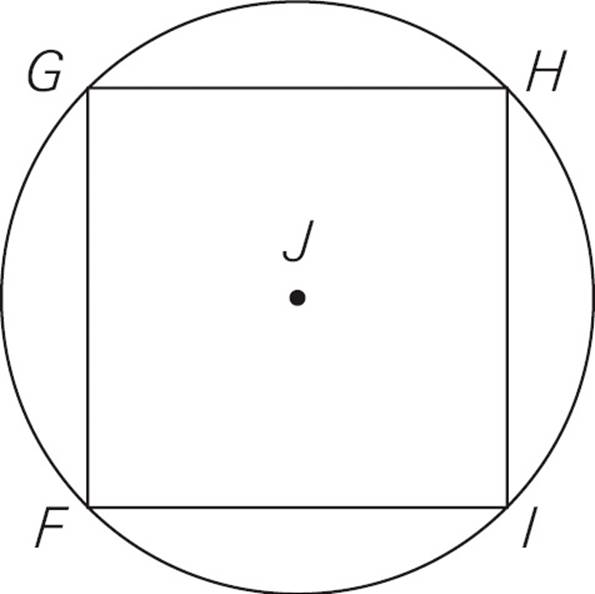
17.In the figure above, FGHI is inscribed in the circle with center J. What is the ratio of the area of FGHI to the area of the circle?
(1) FGHI is a square.
(2) The area of the circle is 8π.
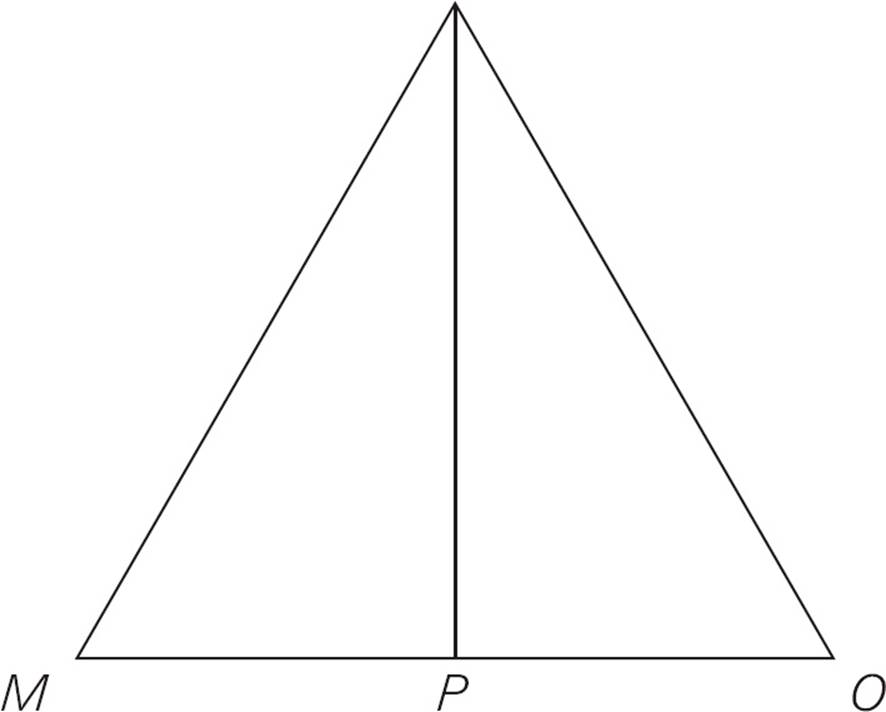
18.In the figure above, triangle MNO is equilateral. What is the area of triangle MNO ?
(1) NP has a length of 5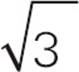 .
.
(2) MN has a length of 10.
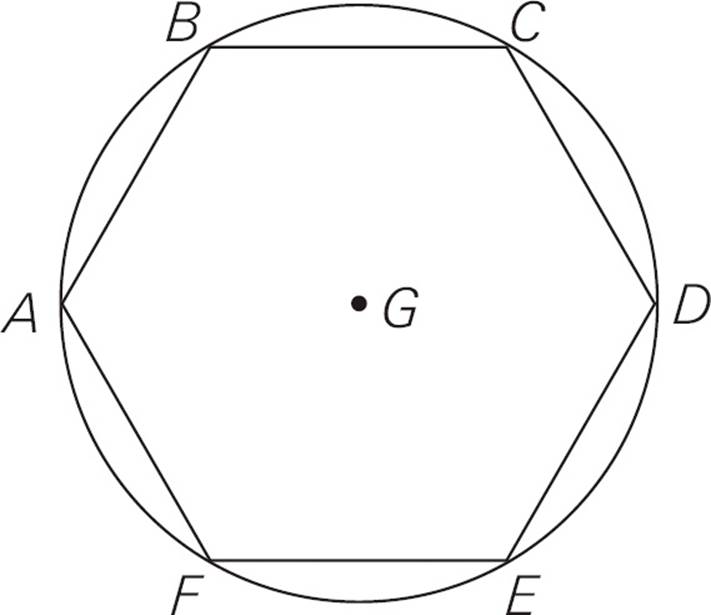
19.In the figure above, equilateral hexagon ABCDEF is inscribed in the circle with center G, which has a diameter of 16. What is the length of AB ?
|
|
16 |
|
|
8 |
|
|
6 |
|
|
8 |
|
|
4 |

Challenge!
Take a crack at this high-level GMAT question.
20.If circle O is inscribed inside of equilateral triangle T, which of the following expresses the ratio of the radius of circle O to one of the sides of triangle T ?
|
|
1 to 2 |
|
|
1 to |
|
|
1 to |
|
|
1 to 2 |
|
|
1 to 2 |
ANSWERS AND EXPLANATIONS
Drill 1
1.EIf the area of the circle is 36π, then the radius is 6. That means AO = 6 and CO = 6. The circumference of the circle is 2 × π × 6 = 12π. Because the slice is 90 out of 360 degrees, it’s a 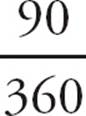 =
= ![]() slice of the circle. So arc ABC is
slice of the circle. So arc ABC is ![]() of the circumference, or
of the circumference, or ![]() × 12π = 3π. So the perimeter of the slice is 6 + 6 + 3π = 12 + 3π. Choose (E).
× 12π = 3π. So the perimeter of the slice is 6 + 6 + 3π = 12 + 3π. Choose (E).
2.CWhen the side that’s 12 inches is cut into three pieces, each piece will measure 4 inches. Therefore, each of the new rectangles will be a square measuring 4 inches by 4 inches. So the perimeter will be 4 + 4 + 4 + 4 = 16 inches. The answer is (C).
Drill 2
1.CIf AB = BC, then the triangle is isosceles and angle C equals angle A, measuring 30 degrees. Angles ADB and CDB form a straight line, so they must add up to 180 degrees. That means angle CDB = 180 − 80 = 100 degrees. You know that a triangle must add up to 180 degrees, so n= 180 − 100 − 30 = 50 degrees. The answer is (C).
2.BIf the square has an area of 100, then each side of the square has a length of 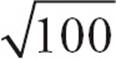 = 10. WXZ is really a 45-45-90 right triangle, so you can apply the ratio. WX and WZ are each 10 units long, so x = 10. That means that XZ, the x
= 10. WXZ is really a 45-45-90 right triangle, so you can apply the ratio. WX and WZ are each 10 units long, so x = 10. That means that XZ, the x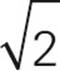 side, is 10
side, is 10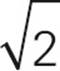 units long. Notice that you can get the same answer by just plugging a = 10 and b = 10 into the a2 + b2 = c2 formula. However, you should also get familiar with the ratio method because there will be problems in which it may be the only thing you can use. Choose (B).
units long. Notice that you can get the same answer by just plugging a = 10 and b = 10 into the a2 + b2 = c2 formula. However, you should also get familiar with the ratio method because there will be problems in which it may be the only thing you can use. Choose (B).
Drill 3
1.AFind the volume of the original cylinder. It’s π × r2 × h = π × 12 × 20 = 20π. The volume doesn’t change when the shape does, so plug that volume into the formula for the new cylinder: v = π × r2 × h becomes 20π = π × 22 × h, so h = 5. Choose (A).
2.CYou can start with (2,5) and work your way down the line by adding −2 to the y coordinate and 3 to the x coordinate. This leads to points (5,3), (8,1), and (11,−1). You can also start at (2,5) and work the other way by adding 2 to y and −3 to x. This leads to (−1,7). You can eliminate all those answers, leaving (C) as the only point not on the line. Choose (C). Alternatively, you can use the given point, (2,5), and the given slope, m = − ![]() , to determine the line equation. Just plug those numbers into the format to get 5 = −
, to determine the line equation. Just plug those numbers into the format to get 5 = −![]() (2) + b. You can solve that for b =
(2) + b. You can solve that for b = 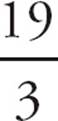 . Then you plug each point into the new line equation to see whether it fits. That way is more tedious, but it will work.
. Then you plug each point into the new line equation to see whether it fits. That way is more tedious, but it will work.
Comprehensive Geometry Drill
1.DOD is the radius of the larger circle, so its area is 100π. If the shaded region is 36π, that leaves 100π − 36π = 64π for the area of the smaller circle. Choose (D).
2.BThis is not only a geometry question, but also a Plugging In question. Suppose the original length is 100 and the original width is 50. The original area is 5,000. The length is reduced by 10% to 90 and the width is reduced by 20% to 40. The new area is 3,600. That’s a decrease of 5,000 − 3,600 = 1,400. To make that a percent change, divide by the original amount: 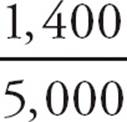 = 28%. Choose (B).
= 28%. Choose (B).
3.DThis is a good problem for Plugging In The Answers. Because the question asks for the greatest area, start with the largest answer and work your way down until you find one that works. E is too large. That rectangle would need a length and width of 2 and 20 or 5 and 8. Those are too big for a perimeter of 20. Next, try (D). A rectangle with an area of 25 could have a length and width of 5 and 5, which gives a perimeter of 20. Choose (D).
4.BUse the coordinates to determine the lengths of the necessary parts. The area of a triangle = ![]() × Base × Height. Since the base must be perpendicular to the height, you can’t just use two sides of the triangle. Instead use the vertical side AC as the base of the triangle and draw a horizontal line from the (5,9) point to the left, as in the figure below. The base AC has a length of 8 because it runs from y = 2 to y = 10. The height (the horizontal line you just drew) has a length of 3 because it goes from x = 2 to x = 5. So the area is
× Base × Height. Since the base must be perpendicular to the height, you can’t just use two sides of the triangle. Instead use the vertical side AC as the base of the triangle and draw a horizontal line from the (5,9) point to the left, as in the figure below. The base AC has a length of 8 because it runs from y = 2 to y = 10. The height (the horizontal line you just drew) has a length of 3 because it goes from x = 2 to x = 5. So the area is ![]() × 8 × 3 = 12. Choose (B).
× 8 × 3 = 12. Choose (B).
5.BDraw a line from B straight down to DC to split the quadrilateral into a rectangle and a triangle. See diagram below. The rectangle has a length and width of 10 and 4, for a total area of 40. The triangle has two sides of 3 and 4. They are perpendicular, so they can serve as the base and height. That gives an area of ![]() × 3 × 4 = 6. So the total area of the quadrilateral is 40 + 6 = 46. Choose (B).
× 3 × 4 = 6. So the total area of the quadrilateral is 40 + 6 = 46. Choose (B).
6.CTriangle MOP is a 30-60-90 right triangle, so use the x : x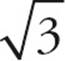 : 2x ratio. MP has a length of 2 and it is the x side (the side opposite the 30-degree angle), so x = 2. MO is the hypotenuse, the 2x side, so it has a length of 2(2) = 4. Choose (C).
: 2x ratio. MP has a length of 2 and it is the x side (the side opposite the 30-degree angle), so x = 2. MO is the hypotenuse, the 2x side, so it has a length of 2(2) = 4. Choose (C).
7.DThe key to overlapping figures is to find the piece that bridges the two figures. In this case, OX and OY are the legs of right triangle XOY, and they are also radii of the circle, so they are equal, which makes OXY a 45-45-90 right triangle. Use the x : x : x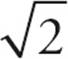 pattern. The hypotenuse is 5, so x
pattern. The hypotenuse is 5, so x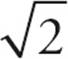 = 5, and x =
= 5, and x = 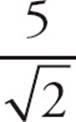 . That means the radius of the circle is r =
. That means the radius of the circle is r = 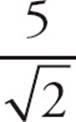 , and the area of the circle is A = πr2 = π
, and the area of the circle is A = πr2 = π 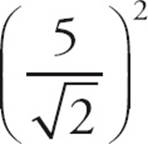 =
= 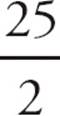 π. Choose (D).
π. Choose (D).
8.BWith a parallel line intersected by another line, only two sizes of angle are created. All of the big angles are equal to 3n and all of the small angles are equal to n. So 3n and n form a straight line and 3n + n = 180. That means that 4n = 180, so n = 45. Choose (B).
9.CIf the area of the square is 25, then each side of the square is 5. ABC is a 45-45-90 right triangle, so use the x : x : x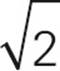 ratio. AB is one of the x sides, so x = 5. Since AC is the x
ratio. AB is one of the x sides, so x = 5. Since AC is the x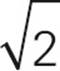 side, it has a length of 5
side, it has a length of 5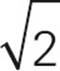 . The radius of the circle is half of AC, or
. The radius of the circle is half of AC, or 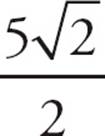 . The area of the circle is πr2= π ×
. The area of the circle is πr2= π × 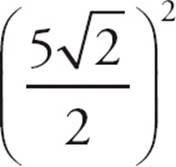 =
= 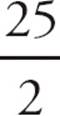 π. Choose (C).
π. Choose (C).
10.DDraw your own diagram and plug in for the variables. Suppose the legs of the triangle are 3 each. The ratio for a 45-45-90 triangle is x : x : x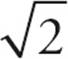 . Since x = 3 (each leg), the hypotenuse is h = 3
. Since x = 3 (each leg), the hypotenuse is h = 3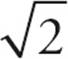 . The area of the triangle is a =
. The area of the triangle is a = ![]() (base)(height) =
(base)(height) = ![]() ×3×3=
×3×3=![]() , so a =
, so a = ![]() . Plug h = 3
. Plug h = 3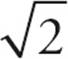 and a =
and a = ![]() into the answers to see which one is true. In answer (D), 4 ×
into the answers to see which one is true. In answer (D), 4 × ![]() = 18 and (3
= 18 and (3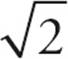 )2 = 18, so choose (D).
)2 = 18, so choose (D).
11.DThe two unshaded regions are vertical angles, so they are equal, at 45 degrees each. Two 45-degree slices are like one 90-degree slice, which is 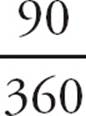 =
= ![]() of the circle, because it covers 90 of the 360 degrees in the circle. That leaves 1 −
of the circle, because it covers 90 of the 360 degrees in the circle. That leaves 1 − ![]() =
= ![]() in the shaded region. Choose (D).
in the shaded region. Choose (D).
12.CThis problem is similar to the Super Pythagorean situation. The longest line segment that can be drawn in the cylinder is one that goes from the edge of the top circle to the opposite edge of the bottom circle. That line is the hypotenuse of a right triangle formed by the height of the cylinder and the diameter of the bottom circle. The diameter of the circle is twice the radius, or 2 × 6 = 12 inches. Given the volume and radius of the cylinder, you can find its height. Plug in 180π for the volume and 6 for the radius into the volume formula: v = πr2h. The result is 180π = π × 62 × h, which becomes h = 5. The legs of the right triangle are 5 and 12. That’s the 5 : 12 : 13 ratio, so the hypotenuse is 13. Choose (C).
13.AStatement (1) tells you that ∠DFE = 90°, so add that to your diagram. (You did draw one on your scratch paper, didn’t you?) Fill in 60° for each of the six angles forming the corners of the two equilateral triangles. Because each triangle has 180°, ∠FDE = 30°. That leads to ∠CDB= 90° and ∠CBD = 30°. If you keep going, you‘ll realize that each of the three small triangles is a 30-60-90 triangle. The middle sides of those triangles are all the same, because they’re sides of an equilateral triangle. Since the triangles all follow the same 30-60-90 ratio, they are all the same size. Suppose the sides of each 30-60-90 triangle are x, x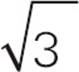 , and 2x. You could use those lengths to find the area of BCD in terms of x. (It’s
, and 2x. You could use those lengths to find the area of BCD in terms of x. (It’s 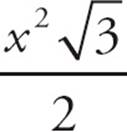 , if you’re curious.) Each side of triangle ACE has a length of x + 2x = 3x. If you drop a height from point C, that forms another 30-60-90 triangle with a hypotenuse of 3x. From there you can find the length of the height, allowing you to find the area of ACE, in terms of x. (It’s
, if you’re curious.) Each side of triangle ACE has a length of x + 2x = 3x. If you drop a height from point C, that forms another 30-60-90 triangle with a hypotenuse of 3x. From there you can find the length of the height, allowing you to find the area of ACE, in terms of x. (It’s 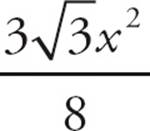 , if you’re curious.) Although you don’t know the actual values, you can find the ratio of the areas. Narrow the choices to (A) and (D). With Statement (2), you’re told the length of AF, but that’s not enough. Remember: You can’t trust the diagram for data sufficiency, only what you’re actually told about the shapes. You don’t know whether the BDF is just a bit smaller than ACE, tilted at just a slight angle, or whether BDF is much smaller than ACE, tilted at a greater angle. That will affect the size of the shaded region, so Statement (2) is insufficient. Choose (A).
, if you’re curious.) Although you don’t know the actual values, you can find the ratio of the areas. Narrow the choices to (A) and (D). With Statement (2), you’re told the length of AF, but that’s not enough. Remember: You can’t trust the diagram for data sufficiency, only what you’re actually told about the shapes. You don’t know whether the BDF is just a bit smaller than ACE, tilted at just a slight angle, or whether BDF is much smaller than ACE, tilted at a greater angle. That will affect the size of the shaded region, so Statement (2) is insufficient. Choose (A).
14.AThe easiest way to solve this one is to use Ballparking. The area of the triangle is 9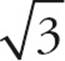 , which is about 15. From the diagram, the shaded region is much smaller than that, maybe 2 or 3. If you convert each answer, only (A) is anywhere close. To really solve this one, draw the height for the equilateral triangle, splitting it into two 30-60-90 triangles. That means you need the x : x
, which is about 15. From the diagram, the shaded region is much smaller than that, maybe 2 or 3. If you convert each answer, only (A) is anywhere close. To really solve this one, draw the height for the equilateral triangle, splitting it into two 30-60-90 triangles. That means you need the x : x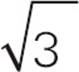 : 2x ratio. Using 2x for the base of triangle XYZ and x
: 2x ratio. Using 2x for the base of triangle XYZ and x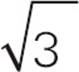 for its height, you can set up the area formula: 9
for its height, you can set up the area formula: 9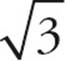 =
= ![]() · 2x · x
· 2x · x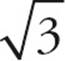 . Solving that, you find x = 3, so each side of XYZ is 6, and so is the radius of the circle. With a radius of 6, the area of the circle is 36π. To find the shaded region, subtract the area of the triangle from the area of the slice of the circle. Since the slice has a 60-degree angle, it is a
. Solving that, you find x = 3, so each side of XYZ is 6, and so is the radius of the circle. With a radius of 6, the area of the circle is 36π. To find the shaded region, subtract the area of the triangle from the area of the slice of the circle. Since the slice has a 60-degree angle, it is a 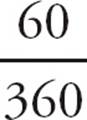 =
= ![]() slice of the circle. That means its area is
slice of the circle. That means its area is ![]() × 36π = 6π. So the area of the shaded region is 6π − 9
× 36π = 6π. So the area of the shaded region is 6π − 9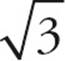 . Wasn’t Ballparking a much simpler approach? Choose (A).
. Wasn’t Ballparking a much simpler approach? Choose (A).
15.EWith Statement (1), you have only one side of the triangle. If that is the height, you still need the base to find the area. Statement (1) is insufficient, so narrow your choices to (B), (C), and (E). Statement (2) presents a similar situation: You have only one side, and you need a base and a height to find the area. Eliminate (B). With both sides, it may appear that you have enough information. It seems that you could plug 3 and 6 into the Pythagorean theorem to find the length of JL and then use the area formula. However, you don’t know which angle in the triangle is 90 degrees. In the figure, it appears that KL is the hypotenuse, but you can’t be sure. If it is the hypotenuse, you get one answer, and if it’s not the hypotenuse, you get another. Therefore, eliminate (C) and choose (E).
16.DWith Statement (1), you could calculate the slope by using the x- and y-coordinates of the two points in the rise-over-run formula. m = 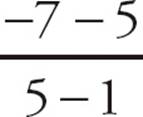 =
= 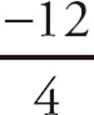 = −3. That’s sufficient, so narrow the choices to (A) and (D). With Statement (2), you can manipulate the equation of the second line to y = −3x + 17, so its slope is −3. Since the lines are parallel, the first line’s slope is also −3. Statement (2) is also sufficient, so choose (D).
= −3. That’s sufficient, so narrow the choices to (A) and (D). With Statement (2), you can manipulate the equation of the second line to y = −3x + 17, so its slope is −3. Since the lines are parallel, the first line’s slope is also −3. Statement (2) is also sufficient, so choose (D).
17.AWith Statement (1), you know the square-looking shape is actually a square. That means the diameter of the circle is equal to the diagonal of the square. You could plug in numbers, such as s = 2 for the side of the square. Using the 45-45-90 ratio, the diagonal would be 2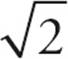 , which gives the circle a radius of
, which gives the circle a radius of 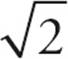 . Since you know the side of the square and the radius of the circle, you could find their areas and compare them in a ratio. Statement (1) is sufficient, so narrow the choices to (A) and (D). With Statement (2), you know the actual area of the circle, but you don’t know anything about FGHI. It could be a square, as it appears, or it could be a very skinny rectangle with little area. Since its area is changeable, you cannot find the ratio of its area to that of the circle. Statement (2) is insufficient, so choose (A).
. Since you know the side of the square and the radius of the circle, you could find their areas and compare them in a ratio. Statement (1) is sufficient, so narrow the choices to (A) and (D). With Statement (2), you know the actual area of the circle, but you don’t know anything about FGHI. It could be a square, as it appears, or it could be a very skinny rectangle with little area. Since its area is changeable, you cannot find the ratio of its area to that of the circle. Statement (2) is insufficient, so choose (A).
18.BStatement (1) may appear to be sufficient. Since the triangle is equilateral, its height will divide it into two 30-60-90 triangles. If you know one of the sides, you can use the 30-60-90 ratio to find the other sides. However, you don’t know that NP is the height of the triangle. It appears that way in the figure, but there’s no concrete indication that it forms a right angle with MO. Statement (1) is insufficient, so narrow your choices to (B), (C), and (E). With Statement (2), you have the length of MN. Since the triangle is equilateral, you can draw the height and use the 30-60-90 ratio to find its length (which turns out to be 5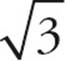 ) and, subsequently, the area of the triangle. Statement (2) is sufficient, so choose (B).
) and, subsequently, the area of the triangle. Statement (2) is sufficient, so choose (B).
19.DStart by drawing a line from the center of the circle to each corner of the hexagon, like spokes of a wheel. Since the hexagon is equilateral, each angle formed by the spokes is equal. There are six of them, so each one is 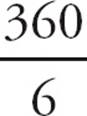 = 60°. Each spoke is a radius of the circle, so they are all equal, meaning that the outer angles of each triangle are equal. Since 60° is already accounted for by the inner angle, each outer angle must be
= 60°. Each spoke is a radius of the circle, so they are all equal, meaning that the outer angles of each triangle are equal. Since 60° is already accounted for by the inner angle, each outer angle must be 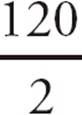 = 60°. So each triangle is an equilateral triangle with sides equal to the radius of the circle, which is 8. Therefore, AB has a length of 8. Choose (D).
= 60°. So each triangle is an equilateral triangle with sides equal to the radius of the circle, which is 8. Therefore, AB has a length of 8. Choose (D).
20.EFirst, draw the height of the equilateral triangle from the tip of the triangle to the base. Since the triangle is equilateral, the height will create a 30 degree angle at the topmost angle. Now, notice that the height passes through the center of the circle. Draw the radius of the circle from the center of the circle to the side on the right. Since the circle is inscribed within the triangle, the radius will create a 90 degree angle at the point it touches the side of the triangle. Now, notice that you have created a right triangle with angle measurements 30, 60, and 90. So, set the radius, which is across from the 30 degree angle, to 1. Since the ratio of the sides of a 30-60-90 right triangle are 1, 1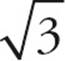 , 2, you can set the side across from the 60 degree angle, or half the side of the equilateral triangle, equal to 1
, 2, you can set the side across from the 60 degree angle, or half the side of the equilateral triangle, equal to 1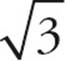 . So, the side of the triangle is 2
. So, the side of the triangle is 2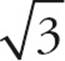 . The ratio is therefore 1 to
. The ratio is therefore 1 to 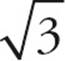 . Choose (E).
. Choose (E).
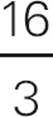
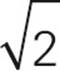
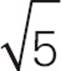
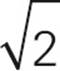
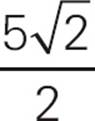 π
π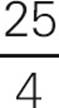 π
π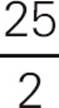 π
π