The history of mathematics: A brief course (2013)
Part III. Greek Mathematics From 500 BCE to 500 CE
Chapter 9. Greek Number Theory
Greek number theory is of interest both intrinsically, because some of the natural questions that it raised have not been answered even in the present time, and because it was the soil in which algebraic symbolism first sprouted, a brilliant innovation during a time otherwise marked by intellectual decline. The theory itself has two areas of interest that do not interact during the period of Greek intellectual dominance. One is the Pythagorean topic of the arithmetic properties of figurate numbers (triangular numbers, square numbers, pentagonal numbers, and so on). This area has declined greatly in importance, along with Pythagoreanism and neo-Platonism, although it is not quite extinct even today. The recent solution of the problem of Fermat's last theorem is a good specimen of the modern development of this theory. The other area, which provides the theoretical foundation for much of classical and modern number theory, is the theory of divisibility of integers. This area also has one rather Pythagorean connection, namely the topic of perfect numbers. We shall look at just three of the classical Greek writers on number theory:
1. Euclid, whose Elements contain three books (Books 7–9) devoted to the divisibility properties of integers.
2. Nicomachus of Gerasa, a neo-Pythagorean philosopher who lived about 100 CE. His Introduction to Arithmetic gives a detailed development of both figurate numbers and the divisibility theory.
3. Diophantus, who lived sometime between the second and fourth centuries CE. He is sometimes justly called the “father of algebra,” because in the course of his study of the arithmetic properties of square numbers, he introduced symbolic notation for an unspecified or unknown number and a way of writing operations on unknown numbers.
As it happens that the treatise of Nicomachus preserves more of what was traditionally called Pythagorean lore than the earlier work of Euclid, we shall discuss Nicomachus first. Before we can do that, however, we need to digress to explain a mathematical technique that is fundamental to the understanding of a great deal in the history of mathematics.
9.1 The Euclidean Algorithm
The Greeks learned early on how to find the greatest common divisor of two numbers. A very efficient procedure for doing so is described in Chapter 13 of Book 1 of Nicomachus' Arithmetica and in Proposition 2 of Book 7 of Euclid's Elements. This procedure is now known as the Euclidean algorithm, Nicomachus applies it only to integers, any two of which naturally have 1 as a common divisor. Euclid, on the other hand, does not confine it to integers, but states the procedure for “magnitudes,” which may lack a common measure. It is significant that when it is applied to continuous magnitudes, the procedure terminates if and only if there is a common measure. Euclid makes use of that fact in discussing incommensurables, which are pairs of magnitudes having no common measure. The algorithm was certainly invented long before the time of Euclid, however. Zverkina (2000) believes that this procedure could not have arisen intuitively, but must have come about as the result of solving specific problems, most likely the problem of reducing ratios by canceling a common divisor. What follows is a description of the general procedure.
For definiteness, we shall imagine that the two quantities whose greatest common measure is to be found are two lengths, say a and b. Suppose that a is longer than b. (If the two are equal, their common value is also their greatest common divisor.) The general procedure is to keep subtracting the smaller quantity from the larger until the remainder is equal to the smaller quantity or smaller than it. It is not difficult to show that the smaller quantity and the remainder have the same common measures as the smaller quantity and the larger. Hence one can start over with the smaller quantity and the remainder, which is no more than half of the larger quantity. Either this process terminates with an equal pair, or it continues and the pairs become arbitrarily small.
An example using integers will make the procedure clear. Let us find the greatest common measure (divisor) of 26173996849 and 180569389. A common measure does exist: the integer 1. Since the repeated subtraction process amounts to division with remainder, we do it this way: 26173996849 ÷ 180569389 is 144 with a remainder of 172004833. We then divide the smaller quantity (the previous divisor) 180569389 by the remainder 172004833, getting a quotient of 1 and a remainder of 8564556. Next we divide the previous remainder 172004833 by the new remainder 8564556, getting a quotient of 20 and a remainder of 713713. We then divide 8564556 by 713713 and get a quotient of 12 with no remainder, so that the greatest common divisor is 713713.
This computation can be arranged as follows, with the successive divisions performed from right to left. The greatest common measure appears at the extreme left:

One can see that this procedure must produce a greatest common measure if one exists, since the first remainder is at most half of the larger of the two original quantities (since it is smaller than the smaller of the two original quantities and not larger than their difference). Similarly, since the smaller quantity becomes the dividend in the second application, the second remainder will be at most half of it. Thus the first two remainders are at most half the size of the original quantities. Yet they are both larger than any common measure the two original quantities had. It follows that if there is any common measure, one of these remainders will ultimately become zero, since repeated halving would otherwise eventually make it smaller than that common measure. The last nonzero remainder is thus the greatest common measure of the two quantities.
9.2 The Arithmetica of Nicomachus
In his first book, Nicomachus makes the elementary distinction between odd and even numbers. Having made this distinction, he proceeds to refine it, distinguishing between even numbers divisible by 4 (evenly even) and those that are not (doubles of odd numbers). He goes on to classify odd numbers in a similar way, thereby coming to the concept of prime and composite numbers. Nicomachus also introduces what we now call pairs of relatively prime numbers. These are pairs of numbers that have no common prime divisor and hence no common divisor except 1. Relational properties were difficult for Greek philosophers, and Nicomachus expresses the concept of relatively prime numbers in a confused manner, referring to three species of odd numbers: the prime and incomposite, the secondary and composite, and “the variety which, in itself, is secondary and composite, but relatively is prime and incomposite.” This way of writing seems to imply that there are three kinds of integers, prime and incomposite, secondary and composite, and a third kind midway between the other two. It also seems to imply that one can look at an individual integer and classify it into exactly one of these three classes. Such is not the case, however. The property of primeness is a property of a number alone. The property of being relatively prime is a property of a pair of numbers. On the other hand, the property of being relatively prime to a given number is a property of a number alone. Nicomachus explains the property in a rather wordy fashion in Chapter 13 of Book 1, where he gives a method of identifying prime numbers that has become famous as the sieve of Eratosthenes.
Nicomachus attributes this method to Eratosthenes (276–174 BCE, best known for this work on prime numbers and for having estimated the size of the earth). To use it, start with a list of all the odd numbers from 3 on, that is,
![]()
From this list, remove the multiples of 3, starting with 3 · 3, that is, remove 9, 15, 21, 27, 33,. . .. The reduced list is then
![]()
From this new list, remove all multiples of 5, starting with 5 · 5. The first nonprime in the resulting list will 49 = 7 · 7, and so you remove all multiples of 7 from that list. In this way, you can generate in short order a complete list of primes up to the square of the first prime whose multiples were not removed. Thus, after removing the multiples of 7, we have the list
![]()
The first nonprime in this list would be 11 · 11 = 121.
9.2.1 Factors vs. Parts. Perfect Numbers
Nicomachus' point of view on this sieve was different from ours. Where we think of the factors of, say 60, as being 2, 2, 3, and 5, Nicomachus thought of the quotients on division by these factors and products of these factors as the parts of a number. Thus, in his language, 60 has the parts 30 (half of 60), 20 (one-third of 60), 15 (one-fourth of 60), 12 (one-fifth of 60), 10 (one-sixth of 60), 6 (one-tenth of 60), 5 (one-twelfth of 60), 4 (one-fifteenth of 60), 3 (one-twentieth of 60), 2 (one-thirtieth of 60), and 1 (one-sixtieth of 60). If these parts are added, the sum is 108, much larger than 60. Nicomachus called such a number superabundant and compared it to an animal having too many limbs. On the other hand, 14 is larger than the sum of its parts. Indeed, it has only the parts 7, 2, and 1, which total 10. Nicomachus called 14 a deficient number and compared it to an animal with missing limbs like the one-eyed Cyclops of the Odyssey. A number that is exactly equal to the sum of its parts, such as 6 = 1 + 2 + 3, he called a perfect number. He gave a method of finding perfect numbers, which remains to this day the only way known to generate such numbers, although it has not been proved that there are no other such numbers. This procedure is also stated by Euclid as Proposition 36 of Book 9 of the Elements: If the sum of the numbers 1, 2, 4,. . ., 2n−1 is prime, then this sum multiplied by the last term will be perfect. To see the recipe at work, start with 1, then double and add: 1 + 2 = 3. Since 3 is prime, multiply it by the last term, that is, 2. The result is 6, a perfect number. Continuing, 1 + 2 + 4 = 7, which is prime. Multiplying 7 by 4 yields 28, the next perfect number. Then, 1 + 2 + 4 + 8 + 16 = 31, which is prime. Hence 31 · 16 = 496 is a perfect number. The next such number is 8128 = 64(1 + 2 + 4 + 8 + 16 + 32 + 64). In this way, Nicomachus was able to generate the first four perfect numbers. He seems to hint at a conjecture, but draws back from stating it explicitly:
When these have been discovered, 6 among the units and 28 in the tens, you must do the same to fashion the next. . .the result is 496, in the hundreds; and then comes 8,128 in the thousands, and so on, as far as it is convenient for one to follow [D'ooge, 1926, p. 211].1
This quotation seems to imply that Nicomachus expected to find one perfect number Nk having k decimal digits. Actually, the fifth perfect number is 33,550,336, so we have jumped from four digits to eight here. The sixth is 8,589,869,056 (10 digits) and the seventh is 137,438,691,328 (12 digits), so that there is no regularity about the distribution of perfect numbers. Thus, Nicomachus was wise to refrain from making conjectures too explicitly. According to Dickson (1919, p. 8), later mathematicians, including the great sixteenth-century algebraist Girolamo Cardano, were less restrained, and this incorrect conjecture has been stated more than once.
For a topic that is devoid of applications, perfect numbers have attracted a great deal of attention from mathematicians. Dickson (1919) lists well over 100 mathematical papers devoted to this topic over the past few centuries. From the point of view of pure number theory, the main questions about them are the following: (1) Is there an odd perfect number?2 (2) Are all even perfect numbers given by the procedure described by Nicomachus?3 (3) Which numbers of the form 2n − 1 are prime? These are called Mersenne primes, after Marin Mersenne (1588–1648), who, according to Dickson (1919, pp. 12–13), first noted their importance, precisely in connection with perfect numbers. Obviously, n must itself be prime if 2n − 1 is to be prime, but this condition is not sufficient, since 211 − 1 = 23 · 89. The set of known prime numbers is surprisingly small, considering that there are infinitely many to choose from, and the new ones being found tend to be Mersenne primes, mostly because that is where people are looking for them. The largest currently known prime, discovered on August 23, 2008, is 243112609 − 1, only the forty-fifth Mersenne prime known at the time. Since then, two more have been discovered, both smaller than this one however.4 It was found by the GIMPS (Great Internet Mersenne Prime Search) project, which links hundreds of thousands of computers via the Internet and runs prime-searching software in the background of each while their owners are busy with their own work. This prime has 12,978,189 decimal digits. Since these primes are not being discovered in ascending order, it is not accurate to call the largest currently known one the 47th Mersenne prime. Exhaustive checking by the GIMPS network since the fortieth Mersenne prime, 220996011 − 1, was discovered on November 17, 2003 (it has 6,320,430 decimal digits) has established that there are no others smaller than that one. Thus we know the first 40 Mersenne primes and seven others as well. In contrast, the largest non-Mersenne prime known as of late 2011 was 19249 · 213018586 + 1, discovered in May 2007; it has 3,918,990 decimal digits and hence is tiny compared with the largest known Mersenne primes. (This information comes from the website http://primes.utm.edu.)
9.2.2 Figurate Numbers
Beginning in Chapter 6 of Book 2, Nicomachus studies figurate numbers: polygonal numbers through heptagonal numbers, and then polyhedral numbers. These numbers are connected with geometry, the number 1 being replaced by a geometric point. To motivate this discussion, Nicomachus speculated that the simplest way to denote any integer would be repeating a symbol for 1 an appropriate number of times. Thus, he said, the number 5 could be denoted α αα α α. This train of thought, if followed consistently, would lead back to a notation even more primitive than the hieroglyphic notation for numbers, since it would use only the symbol for units and discard the symbols for higher powers of 10. The Egyptians had gone beyond this principle in their hieratic notation, and the standard Greek notation was essentially a translation of the hieratic into the Greek alphabet. You can easily see where this speculation leads. The outcome is shown in Fig. 9.1, which illustrates triangular, square, pentagonal, and hexagonal numbers using dots instead of the letter α. Observe that the figures are not associated with regular polygons except in the case of triangles and squares. The geometry alone makes it clear that a square number is the sum of the corresponding triangular number and its predecessor. Similarly, a pentagonal number is the sum of the corresponding square number and the preceding triangular number, a hexagonal number is the sum of the corresponding pentagonal number and the preceding triangular number, and so forth. This is the point at which modern mathematics parts company with Nicomachus, Proclus, and other philosophers who push analogies further than the facts will allow. As Nicomachus states at the beginning of Chapter 7:
The point, then, is the beginning of dimension, but not itself a dimension, and likewise the beginning of a line, but not itself a line; the line is the beginning of surface, but not surface; and the beginning of the two-dimensional, but not itself extended in two dimensions. . .Exactly the same in numbers, unity is the beginning of all number that advances unit by unit in one direction; linear number is the beginning of plane number, which spreads out like a plane in one more dimension. [D'ooge, 1926, p. 239]
This mystical mathematics was transmitted to Medieval Europe by Boethius. It is the same kind of analogical thinking found in Plato's Timaeus, where it is imagined that atoms of fire are tetrahedra, atoms of earth are cubes, and so forth. Since the Middle Ages, this topic has been of less interest to mathematicians. The phrase of less interest—rather than of no interest—is used advisedly here: There are a few theorems about figurate numbers in modern number theory, and they have some connections with analysis as well. For example, a formula of Euler asserts that
![]()
Here the exponents on the right-hand side range over the pentagonal numbers for n positive. By defining the nth pentagonal number for negative n to be n(3n − 1)/2, we gain an interesting formula that can be stated in terms of figurate numbers. Carl Gustav Jacobi (1804–1851) was pleased to offer a proof of this theorem as evidence of the usefulness of elliptic function theory. Even today, these numbers crop up in occasional articles in graph theory and elsewhere.
Figure 9.1 Figurate numbers. Top row: triangular numbers Tn = n(n + 1)/2. Second row: square numbers Sn = n2. Third row: pentagonal numbers Pn = n(3n − 1)/2. Bottom row: hexagonal numbers Hn = n(2n − 1).

9.3 Euclid's Number Theory
Euclid devotes most of his three books on number theory to divisibility theory, spending most of the time on proportions among integers and on prime and composite numbers, with fewer results on figurate numbers. Only at the end of Book 9 does he prove a theorem of a different sort, giving the method of constructing perfect numbers described above. It is interesting that, except for squares and cubes, Euclid does not mention figurate numbers. Although the Pythagorean and Platonic roots of Euclid's treatise are obvious, Euclid appears to the modern eye to be much more a mathematician than Pythagoras or Plato, not at all inclined to flights of fanciful speculation on the nature of the universe. In fact, he never mentions the universe at all and suggests no practical applications of the theorems in his Elements.
Book 7 develops proportion for positive integers as part of a general discussion of ways of reducing a ratio to lowest terms. The notion of relatively prime numbers is introduced, and the elementary theory of divisibility is developed as far as finding least common multiples and greatest common factors. Book 8 resumes the subject of proportion and extends it to squares and cubes of integers, including the interesting theorem that the mean proportional of two square integers is an integer (Proposition 11—for example, 25 : 40 : : 40 : 64), and between any two cubes there are two such mean proportionals (Proposition 12—for example, 27 : 45 : : 45 : 75 : : 75 : 125). Book 9 continues this topic; it also contains the famous theorem that there are infinitely many primes (Proposition 20, in the form of the assertion that no given finite collection of primes can contain all of them) and ends by giving the only known method of constructing perfect numbers (Proposition 36), quoted above.
Euclid's number theory does not contain any explicit statement of the fundamental theorem of arithmetic (Knorr, 1976). This theorem, which asserts that every positive integer can be written in only one way as a product of prime numbers, can easily be deduced from Book 7, Proposition 24: If two numbers are relatively prime to a third, their product is also relatively prime to it.
9.4 The Arithmetica of Diophantus
Two works of Diophantus have survived in part, a treatise on polygonal numbers and the work for which he is best known, the Arithmetica. Like many other ancient works, these two works of Diophantus survived because of the efforts of a ninth-century Byzantine mathematician named Leon, who organized a major effort to copy and preserve them. There is little record of the influence the works of Diophantus may have exerted before this time. What is of particular interest to us is his study of the arithmetic properties of squares. He is interested in finding ways to represent a given rational square number as the sum of two other rational square numbers. The techniques he developed to solve that problem resulted in the first use of symbolism to represent the kind of abstract thinking required in algebra.
To judge this work, one should know something of its predecessors and its influence. Unfortunately, information about either of these is difficult to come by. The Greek versions of the treatise, of which there are 28 manuscripts according to Sesiano (1982, p. 14), all date to the thirteenth century. Among the predecessors of Diophantus, we can count Heron of Alexandria and one very obscure Thymaridas, who showed how to solve a particular set of linear equations, known as the epanth![]() ma (blossom) of Thymaridas.
ma (blossom) of Thymaridas.
Because the work of Diophantus is so different from the style of Euclid and his immediate successors, the origins of his work have been traced to other cultures, notably Egypt and Mesopotamia. The historian of mathematics Paul Tannery (1843–1904) printed an edition of Diophantus' work and included a fragment supposedly written by the eleventh-century writer Michael Psellus (1018–ca. 1078), which stated that “As for this Egyptian method, while Diophantus developed it in more detail,. . ..” On this basis, Tannery assigned Diophantus to the third century. Neugebauer (1952, p. 80) distinguished two threads in Hellenistic mathematics, one in the logical tradition of Euclid, the other having roots in the Babylonian and Egyptian procedures and says that, “the writings of Heron and Diophantus. . .form part of this oriental tradition which can be followed into the Middle Ages both in the Arabic and in the western world.” Neugebauer saw Diophantus as reflecting an earlier type of mathematics practiced in Greece alongside the Pythagorean mathematics and temporarily eclipsed by the Euclidean school. As he said (1952, p. 142):
It seems to me characteristic, however, that Archytas of Tarentum could make the statement that not geometry but arithmetic alone could provide satisfactory proofs. If this was the opinion of a leading mathematician of the generation just preceding the birth of the axiomatic method, then it is rather obvious that early Greek mathematics cannot have been very different from the Heronic Diophantine type.
9.4.1 Algebraic Symbolism
Diophantus began by introducing a symbol for a constant unit ![]() , from monás
, from monás ![]() , along with a symbol for an unknown number ς, conjectured to be an abbreviation of the first two letters of the Greek word for number: arithmós
, along with a symbol for an unknown number ς, conjectured to be an abbreviation of the first two letters of the Greek word for number: arithmós ![]() . For the square of an unknown he used Δυ, the first two letters of dýnamis
. For the square of an unknown he used Δυ, the first two letters of dýnamis ![]() , meaning power. For its cube he used Kυ,the first two letters of kýbos
, meaning power. For its cube he used Kυ,the first two letters of kýbos ![]() , meaning cube. He then combined these letters to get fourth (ΔυΔ), fifth (ΔKυ), and sixth (KυK) powers. For the reciprocals of these powers of the unknown he invented names by adjoining the suffix -ton (-τoν)to the names of the corresponding powers. These various powers of the unknown were called eída
, meaning cube. He then combined these letters to get fourth (ΔυΔ), fifth (ΔKυ), and sixth (KυK) powers. For the reciprocals of these powers of the unknown he invented names by adjoining the suffix -ton (-τoν)to the names of the corresponding powers. These various powers of the unknown were called eída ![]() , meaning species. Diophantus' system for writing down the equivalent of a polynomial in the unknown consisted of writing down these symbols in order to indicate addition, each term followed by the corresponding number symbol (for which the Greeks used their alphabet). Terms to be added were placed first, separated by a pitchfork
, meaning species. Diophantus' system for writing down the equivalent of a polynomial in the unknown consisted of writing down these symbols in order to indicate addition, each term followed by the corresponding number symbol (for which the Greeks used their alphabet). Terms to be added were placed first, separated by a pitchfork ![]() from those to be subtracted. Heath conjectured that this pitchfork symbol is a condensation of the letters lambda and iota, the first two letters of a Greek root meaning less or leave. Thus what we would call the expression 2x4 − x3 − 3x2 + 4x + 2 would be written
from those to be subtracted. Heath conjectured that this pitchfork symbol is a condensation of the letters lambda and iota, the first two letters of a Greek root meaning less or leave. Thus what we would call the expression 2x4 − x3 − 3x2 + 4x + 2 would be written ![]() .
.
Diophantus' use of symbolism is rather sparing by modern standards. He often uses words where we would use symbolic manipulation. For this reason, his algebra was described by the nineteenth-century German orientalist Nesselmann (1811–1881) as a transitional “syncopated” phase between the earliest “rhetorical” algebra, in which everything is written out in words, and the modern “symbolic” algebra.
9.4.2 Contents of the Arithmetica
According to the introduction to the Arithmetica, this work consisted originally of 13 books, but until recently only six were known to have survived. It was assumed that these were the first six books, on which Hypatia was known to have written a commentary. However, more books were recently found in an Arabic manuscript that the experts say is a translation made very early—probably in the ninth century. Sesiano (1982) stated that these books are in fact the books numbered 4 to 7, and that the books previously numbered 4 to 6 must come after them.
Diophantus begins with a small number of determinate problems that illustrate how to think algebraically using the symbolic notation discussed above. Indeterminate problems, which are number theory because the solutions are required to be rational numbers (the only kind recognized by Diophantus), begin in Book 2.5 A famous example of this type is Problem 8 of Book 2: Separate a given square number into two squares. Diophantus illustrates this problem using the number 16 as an example. His method of solving this problem is to express the two numbers in terms of a single unknown ς in such a way that one of the conditions is satisfied automatically. Thus, letting one of the two squares be ς2, which Diophantus wrote as Δυ, he noted that the other will automatically be 16 − ς2. To get a determinate equation for ς, he assumes that the other number to be squared is 4 less than an unspecified multiple of ς. The number 4 is chosen because it is the square root of 16. In our terms, it leads to a quadratic equation one of whose roots is zero, so that the other root can be found by solving a linear equation. As we would write it, assuming that 16 − ς2 = (kς − 4)2, we find that (k2 + 1)ς2 = 8kς, and—canceling ς, since Diophantus does not operate with 0—we get ς = 8k/(k2 + 1). This formula generates a whole infinite family of solutions of the equation that we would call x2 + y2 = 16 via the identity
![]()
You may be asking why it was necessary to use a square number (16) here. Why not separate any positive rational number, say 5, into a sum of two squares? If you look carefully at the solution, you will see that Diophantus had to make the constant term drop out of the quadratic equation, and that could only be done by introducing the square root of the given number.
Diophantus' procedure is slightly less general than what we have just shown, although his illustrations show that he knows the general procedure and could generate other solutions. In his illustration he assumes that the other square is (2ς − 4)2. Since this number must be 16 − ς2, he finds that 4ς2 − 16ς + 16 = 16 − ς2, so that ![]() . It is clear that this procedure can be applied very generally, with the coefficient 2 replaced by any positive integer, showing an infinite number of ways of dividing a given square into two other squares.
. It is clear that this procedure can be applied very generally, with the coefficient 2 replaced by any positive integer, showing an infinite number of ways of dividing a given square into two other squares.
At first sight it appears that number theory really is not involved in this problem, that it is a matter of pure algebra. This topic, however, naturally leads to other questions that definitely do involve number theory, that is, the theory of divisibility of integers. The most obvious one is the problem of finding all possible representations of a positive rational number as the sum of the squares of two rational numbers. One could then generalize and ask how many ways a given rational number can be represented as the sum of the cubes or fourth powers, and so forth, of two rational numbers. Those of a more Pythagorean bent might ask how many ways a number can be represented as a sum of triangular, pentagonal, or hexagonal numbers. In fact, many questions like this have been asked. Leonhard Euler (1707–1783) proved that it was impossible for the sum of fewer than three cubes to equal a cube and conjectured that it was impossible for the sum of fewer than n nth powers to equal another nth power. (He was wrong: It is possible for for the sum of four fifth powers to equal a fifth power.)
9.4.3 Fermat's Last Theorem
The problem just solved achieved lasting fame when Fermat, who was studying the Arithmetica, remarked that the analogous problem for cubes and higher powers had no solutions; that is, one cannot find positive integers x, y, and zsatisfying x3 + y3 = z3 or x4 + y4 = z4, or, in general, xn + yn = zn with n > 2. Fermat stated that he had found a proof of this fact, but unfortunately did not have room to write it in the margin of the book. Fermat never published any general proof of this fact, although the special case n = 4 is a consequence of a method of proof developed by Fermat, known as the method of infinite descent. The problem became generally known after 1670, when Fermat's son published an edition of Diophantus' work along with Fermat's notes. It was a tantalizing problem because of its comprehensibility. Anyone with a high-school education in mathematics can understand the statement of the problem, and many mathematicians dreamed of solving it when they were young. Despite the efforts of hundreds of amateurs and prizes offered for the solution, no correct proof was found for more than 350 years. On June 23, 1993, the British mathematician Andrew Wiles (b. 1953) announced at a conference held at Cambridge University that he had succeeded in proving a certain conjecture in algebraic geometry known as the Shimura–Taniyama conjecture, from which Fermat's conjecture is known to follow. This was the first claim of a proof by a reputable mathematician using a technique that is known to be feasible, and the result was tentatively endorsed by other mathematicians of high reputation. After several months of checking, some doubts arose. Wiles had claimed in his announcement that certain techniques involving what are called Euler systems could be extended in a particular way, and this extension proved to be doubtful. In collaboration with another British mathematician, Richard Taylor, Wiles eventually found an alternative approach that simplified the proof considerably, and there is now no doubt among the experts in number theory that the problem has been solved.
To give another illustration of the same method, we consider the problem following the one just discussed, that is, Problem 9 of Book II: Separate a given number that is the sum of two squares into two other squares. (That is, given one representation of a number as a sum of two squares, find a new representation of the same type.) Diophantus shows how to do this using the example 13 = 22 + 32. He lets one of the two squares be (ς + 2)2 and the other (2ς− 3)2, resulting in the equation 5ς2 − 8ς = 0. Thus, ![]() , and indeed
, and indeed ![]() . It is easy to see here that Diophantus is deliberately choosing a form for the solution that will cause the constant term to drop out. This amounts to a general method, used throughout the first two books, and based on the proportion
. It is easy to see here that Diophantus is deliberately choosing a form for the solution that will cause the constant term to drop out. This amounts to a general method, used throughout the first two books, and based on the proportion
![]()
for solving the equation X2 + Y2 = a2.
The method Diophantus used to solve such problems in his first two books was conjectured by Maximus Planudes (1255–1305) and has recently been explained in simple language by Christianidis (1998).
Some of Diophantus' indeterminate problems reach a high degree of complexity. For example, Problem 19 of Book 3 asks for four numbers such that if any of the numbers is added to or subtracted from the square of the sum of the numbers, the result is a square number. Diophantus gives the solutions as
![]()
Problems and Questions
Mathematical Problems
9.1 Use the fact that the greatest common divisor of 26173996849 and 180569389 is 713713 to reduce the fraction ![]() to lowest terms.
to lowest terms.
9.2 The Euclidean algorithm focuses on the remainders in the division process and has nothing to say about the quotients. Note that the quotients in the example given above were (in order of division) 144, 1, 20, and 12. Consider the continued fraction
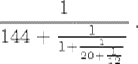
Evaluate this fraction, and compare it with the result of the preceding exercise. We shall have further use for the quotients in the Euclidean algorithm when we study the mathematics of the Hindus.
9.3 Verify that
![]()
See L. J. Lander and T. R. Parkin, “Counterexample to Euler's conjecture on sums of like powers,” Bulletin of the American Mathematical Society, 72 (1966), p. 1079. Smaller counterexamples to this conjecture have been discovered more recently.
Historical Questions
9.4 What are the main topics investigated in ancient Greek number theory?
9.5 What mathematical ideas were ascribed to the Pythagoreans by ancient commentators?
9.6 What innovation in mathematics arises in the number-theoretic investigations of Diophantus?
Questions for Reflection
9.7 For what reason would the ancient Greeks have been investigating figurate numbers, perfect numbers, and the like? Did they have a practical application for these ideas?
9.8 How much of number theory has a practical application nowadays? (If you don't know about RSA codes, for example, look them up on-line.)
9.9 Should the work of Diophantus be classified as primarily number theory or primarily algebra?
Notes
1. D'ooge illustrates the procedure in a footnote, but states erroneously that 8191 is not a prime.
2. The answer is unknown at present.
3. The answer is yes. The result is amazingly easy to prove, but no one seems to have noticed it until a posthumous paper of Leonhard Euler gave a proof. Victor-Amédée Lebesgue (1791–1875) published a short proof in 1844.
4. The reader will correctly infer from previous footnotes that exactly 47 perfect numbers are now known.
5. Although Diophantus allowed solutions to be what we now call positive rational numbers, the name Diophantine equation is now used to refer to an indeterminate equation or system in which the solutions are required to be integers.