The history of mathematics: A brief course (2013)

Part III. Greek Mathematics From 500 BCE to 500 CE

Chapter 11. Athenian Mathematics I: The Classical Problems

The fifth century BCE was the high-water mark of Athenian power. The Ionian islands were constantly menaced and often subjugated by the Persian Empire, which also occasionally threatened the mainland of Greece. In 490 BCE, the Athenians stood alone and fought off a Persian invasion at the Battle of Marathon, thereby increasing their prestige among the Greek city–states. Ten years later, when another invasion was imminent, the famous 300 Spartans commanded by Leonidas, along with about a thousand others, held off the Persians for several days before being overwhelmed by the superior numbers of the Persian army at Thermopylae. This victory allowed the Persians to invade Greece and sack Athens, but the Greek naval forces led by the Athenians defeated the Persian navy at Salamis, forcing the Persians to delay the conquest of the rest of Greece. The following year, they were defeated by a combined Greek force at Platæa. Once the Persian threat was beaten back, the Spartans withdrew into isolationism, while the Athenians vigorously promoted a Greek defense league, with themselves at the head of it. Athens became quite prosperous during the period of peace. Some of the magnificent buildings whose ruins still inspire the visitor were built during the time of Pericles' leadership of the city (461–429). It was during this time that the philosopher Anaxagoras (ca. 500–428) came to Athens and eventually was arrested on the charge of denying that the sun was the god Helios. (He taught that it was a hot stone the size of the Peloponnesus.) While in prison, he allegedly worked on the problem of squaring the circle.

In 431 BCE, war broke out between Sparta and Athens and raged intermittently for the next quarter-century. Fortune seemed to turn against the Athenians on nearly every occasion, and finally, in 404 BCE, they capitulated. The Spartans had no desire to colonize or rule Athens; and they quickly restored the Athenian government, which proceeded to take revenge on the aristocrats who had sided or appeared to side with the Spartans. Among the victims was the philosopher Socrates (ca. 470–399), one of whose followers was Plato, also a member of an aristocratic family. After Socrates' death, Plato journeyed to Sicily, where he is said to have met the Pythagorean philosopher Philolaus. Returning to Athens, he founded his famous Academy in 387 BCE.

Plato's main interest, conditioned no doubt by his experience of war and defeat, was in political questions. He wished to get the very best people to rule. Among the virtues, he placed a high value on knowledge and wisdom, and through that route he became interested in mathematical questions. Some of his students worked on mathematical problems. Because of this shift in the intellectual center of gravity from the commercial Greek colonies to Athens, we are going to call the geometry developed during the late fourth century BCE and throughout the third century Athenian mathematics, even though not all of it was done in Athens. One of its highest achievements, the solution of the problem of incommensurables by Eudoxus, was the work of a former disciple of Plato who had moved on and established himself elsewhere as a prominent geometer and astronomer.

Plato's most famous student, Aristotle (384–322), left the Academy just before the death of Plato and set up his own school, the Lyceum, over the hill in Athens from the Academy. His most famous pupil was Alexander (son of Philip of Macedon), later to be known as Alexander the Great.¹ The Macedonians conquered the Greek mainland and expanded their control over the entire Middle East, crushing the Persian Empire at the Battle of Arbela in 331 BCE. After conquering Egypt, Alexander founded a new city in the Nile Delta, naming it after himself. In that city, his general Ptolemy Soter, who succeeded him as ruler of that portion of the Macedonian Empire, founded the famous Library, at which the great mathematicians of the third century BCE all studied.

Let us now proceed to examine this work that we are calling Athenian mathematics. In the present chapter, we shall discuss only the progress made on the three unsolved classical problems mentioned in the preceding chapter. The all-important work on the theory of incommensurables, and the logical ordering of the material will be discussed in the next chapter, which is devoted to the schools of Plato and Aristotle.

The problems of doubling the cube and trisecting the angle were solved, to the extent that they can be solved, during this period. Even so, new methods of solving them continued to be sought long afterward; and the quadrature of the circle, a much more difficult problem, was never solved in a satisfactory way. In order to tell as full a story as possible, we shall extend our discussion of these three classical problems beyond the period that we have characterized as Athenian mathematics.

11.1 Squaring the Circle

Proclus mentions Hippocrates of Chios as having discovered the quadratures of lunes. This mathematician (ca. 470–ca. 410 BCE), who lived in Athens at the time of the Peloponnesian War, is said to have worked on all three of the classical problems. A lune is a figure resembling a crescent moon: the region inside one of two intersecting circles and outside the other. In the ninth volume of his commentary on Aristotle's books on physics, the sixth-century commentator Simplicius discusses several lunes that Hippocrates squared, including the one depicted in Fig. 11.1. After detailing the criticism by Eudemus of earlier attempts by the Sophist Antiphon (480–411) to square the circle by polygonal approximation, Simplicius reports the quadrature shown in (Fig. 11.1), which uses a result that later appeared in Book 12 of Euclid's Elements. The result needed is that semicircles are proportional to the squares on their diameters. How that fact was established will be taken up in the next chapter. In the meantime, we note that if is the radius of the large semicircle AΓBΔ, then the radius of the smaller semicircle AΔE is . The segment of the larger semicircle inside the smaller one is obviously half of the larger semicircle less the triangle AΓΔ. In our terms, the segment has area , while the area of the smaller semicircle is . Therefore the lune, which is the difference of these two figures, has area equal to the triangle. Thus, quadrature of some figures bounded by circular arcs is possible, since this lune is demonstrably equal to a figure bounded by straight lines.

Figure 11.1 Hippocrates' quadrature of a lune, acording to Simplicius.

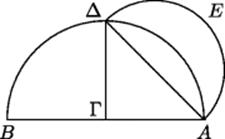
Simplicius' reference to Book 12 of Euclid's Elements is anachronistic, since Hippocrates lived before Euclid; but it was probably well known that similar circular segments are proportional to the squares on their bases. Even that theorem is not needed here, except in the case of semicircles, and that special case is easy to derive from the theorem for whole circles. The method of Hippocrates does not achieve the quadrature of a whole circle; we can see that his procedure works because the “irrationalities” of the two circles cancel each other when the segment of the larger circle is removed from the smaller semicircle.

In his essay On Exile, Plutarch reports that the philosopher Anaxagoras worked on the quadrature of the circle while imprisoned in Athens. Other attempts are reported, one by Dinostratus (ca. 390–ca. 320 BCE), the brother of Menaechmus. Dinostratus is said to have used the curve called (later, no doubt) the quadratrix, (squarer), said to have been invented by Hippias of Elis (ca. 460–ca. 410 BCE) for the purpose of trisecting the angle. It is discussed below in that connection.

11.2 Doubling the Cube

Although the problem of doubling the cube fits very naturally into what we have imagined as a purely geometric program—to extend the achievements in transformation of areas into similar results in the transformation of volumes—some ancient authors gave it a more exotic origin. In The Utility of Mathematics, Theon of Smyrna discusses a work called Platonicus that he ascribes to Eratosthenes. In that work, the citizens of Delos (the island that was the headquarters of the Athenian Empire) consulted an oracle in order to be relieved of a plague, and the oracle told them to double the size of an altar.2 According to Theon, Eratosthenes depicted the Delians as having turned for technical advice to Plato, who told them that the altar was not the point: The gods really wanted the Delians to learn geometry better. In his commentary on Archimedes' work on the sphere and cylinder, Eutocius gives another story, also citing Eratosthenes, but he says that Eratosthenes told King Ptolemy in a letter that the problem arose on the island of Crete when King Minos ordered that a tomb built for his son be doubled in size.

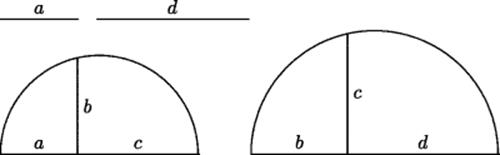
Whatever the origin of the problem, both Proclus and Eutocius agree that Hippocrates was the first to reduce it to the problem of two mean proportionals. The fifth-century geometers knew that the mean proportional between any two square integers is an integer (for example, ) and that between any two cubes such as 8 and 216 there are two mean proportionals (Euclid, Book 8, Propositions 11 and 12); for example, 8 : 24 : : 24 : 72 : : 72 : 216. If two mean proportionals could be found between the sides of two cubes—as seems possible, since every volume can be regarded as the cube on some line—the problem would be solved. It would therefore be natural for Hippocrates to think along these lines, by analogy with the result on figurate numbers, when comparing two cubes. Eutocius, however, was somewhat scornful of this reduction, saying that the new problem was just as difficult as the original one. That claim, however, is not true: One can easily draw a figure containing two lines and their mean proportional (Fig. 11.2): the two parts of the diameter on opposite sides of the endpoint of the half-chord of a circle and the half-chord itself. The only problem is to get two such figures with the half-chord and one part of the diameter reversing roles between the two figures and the other parts of the diameters equal to the two given lines, as shown in Fig. 11.2. It is natural to think of using two semicircles for this purpose and moving the chords to meet these conditions.

Figure 11.2 The problem of two mean proportionals: Given a and d, find b and c.

In his commentary on the treatise of Archimedes on the sphere and cylinder, Eutocius gives a number of solutions to this problem, ascribed to various authors, including Plato. The earliest one that he reports is due to Archytas (ca. 428–350 BCE). This solution requires intersecting a cylinder with a torus and a cone. The three surfaces intersect in a point from which the two mean proportionals can be determined. A later solution by Menaechmus may have arisen as a simplification of Archytas' rather complicated construction. It requires intersecting two cones, each having a generator parallel to a generator of the other, with a plane perpendicular to both generators. These intersections form two conic sections, a parabola and a rectangular hyperbola; where they intersect, they produce the two mean proportionals, as shown in Fig. 11.7.

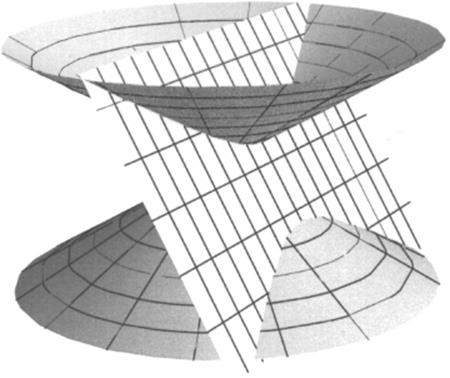
If Eutocius is correct, the conic sections first appeared, but not with the names they now bear, in the fourth century BCE. Menaechmus created these sections by cutting a cone with a plane perpendicular to one of its generators. When that is done, the shape of the section depends on the apex angle of the cone. If that angle is acute, the section will be an ellipse; if it is a right angle, the section will be a parabola; if it is obtuse, the section will be a hyperbola. In the commentary on Archimedes' treatise on the sphere and cylinder mentioned above, Eutocius tells how he happened to find a work written in the Doric dialect which seemed to be a work of Archimedes. He mentions in particular that instead of the word parabola, used since the time of Apollonius, the author used the phrase section of a right-angled cone; and instead of hyperbola, he used the phrase section of an obtuse-angled cone. Since Proclus refers to “the conic section triads of Menaechmus,” it is inferred that the original names of the conic sections were oxytom (sharp cut), orthotom (right cut), and amblytom (blunt cut), as shown in Figs. 11.3–11.5. However, Menaechmus probably thought of the cone as the portion of the figure from the vertex to some particular circular base, since the Greeks did not consider infinitely extended bodies. In particular, he wouldn't have thought of the hyperbola as having two nappes, as we now do.

Figure 11.3 The oxytome (ellipse) of Menaechmus, obtained by cutting an acute-angled cone by a plane perpendicular to a generator.

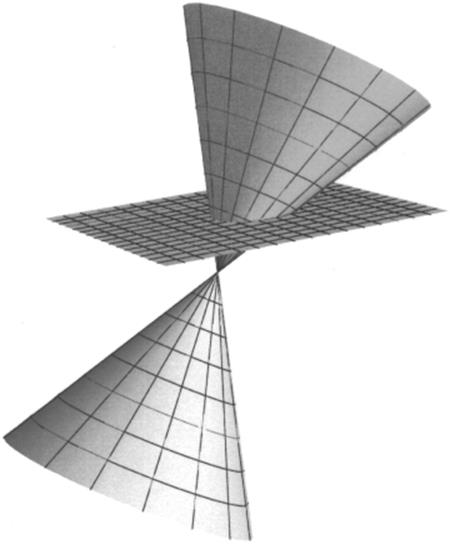
Figure 11.4 The orthotome (parabola) of Menaechmus, obtained by cutting a right-angled cone by a plane perpendicular to a generator.

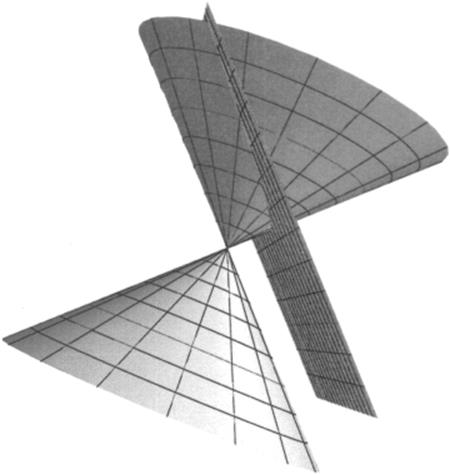
Figure 11.5 The amblytome (hyperbola) of Menaechmus, obtained by cutting an obtuse-angled cone by a plane at right angles to a generator.

How Apollonius of Perga came to give them their modern names a century later is described below. At present, we shall look at the consequences of Menaechmus' approach and see how it enabled him to solve the problem of two mean proportionals. It is very difficult for a modern mathematician to describe this work without breaking into modern algebraic notation, essentially using analytic geometry. It is very natural to do so, because Menaechmus, if Eutocius reports correctly, comes very close to stating his theorem in algebraic language. To describe this work in Menachmus' original language would require far more space than we have available and would be tedious and confusing. Thus, with apologies for the inevitable distortion, we shall abbreviate the discussion and use some algebraic symbolism.

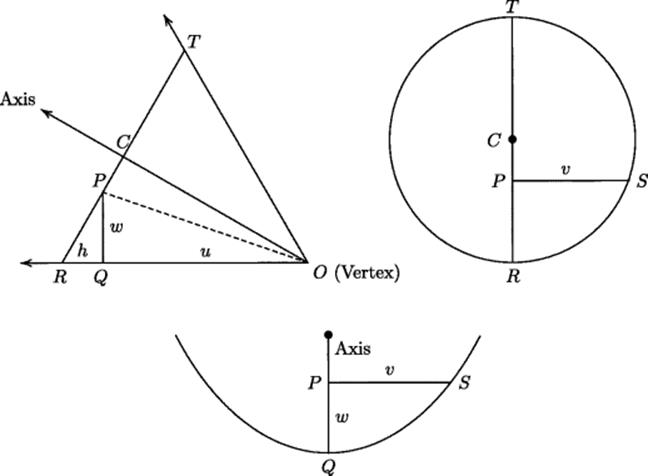
We begin by looking at a general conic section, shown in Fig. 11.6. When a cone is cut by a plane through its axis, the resulting figure is simply a triangle, called the axial triangle. The end that we have left open by indicating with arrows the direction of the axis and two generators in this plane would have been closed off by Menaechmus. If the cone is cut by a plane perpendicular to its axis, the result is a circle. The conic section is obtained as the intersection with a plane perpendicular to one of its generators at a given distance (marked u in the figure) from the apex. The important relation needed is the one between the length of a horizontal chord (double the length marked ) in the conic section and its height (marked ) above the generator that has been cut. Using only similar triangles and the fact that a half chord in a circle is the mean proportional between the segments of the diameter through its endpoint, Menaechmus derived the fundamental relation that we write as

Although we have written this relation as an equation with letters in it, Menaechmus would have been able to describe what it says in terms of the lines , u, h, and , and squares and rectangles on them. He would have known the value of the ratio , which is determined by the shape of the triangle ROC. In our terms , where ϕ is the apex angle of the cone. When conic sections are to be applied, the user has free choice of the apex angle ϕand the length u.

Figure 11.6 Sections of a cone. Top left: through the axis. Top right: perpendicular to the axis. Bottom: perpendicular to the generator OR at a point Q lying at distance u from the vertex O. The fundamental relation is . The length h has a fixed ratio to , depending only on the shape of the triangle OCR.

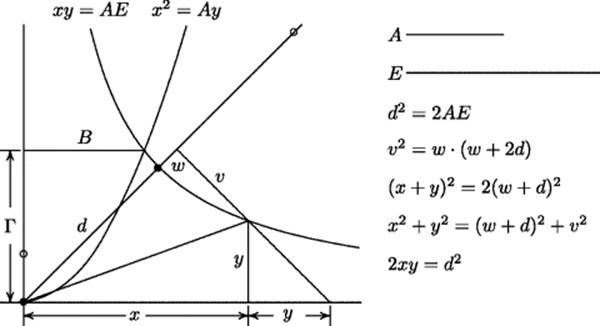
The simplest case is that of the parabola, where the apex angle is 90° and . In that case the relation between and is

In the problem of putting two mean proportionals B and Γ between two lines A and E, Menaechmus took the u for this parabola to be , so that .

The hyperbola Menaechmus needed for this problem was a rectangular hyperbola, which results when the triangle ROC is chosen so that , and therefore . Such a triangle is easily constructed by extending one side of a square to the same length as the diagonal and joining the endpoint to the opposite corner of the square. In any triangle of this shape the legs are the side and diagonal of a square. In this case, the apex angle of the cone is about 109 . 4° or 1.910634 radians, and we get . For that case Menaechmus would have been able to show that

that is,

where d () is the diagonal of a square whose side is u. To solve the problem of two mean proportionals, Menaechmus took ; that is, the mean proportional between A and E. Menaechmus' solution is shown in Fig. 11.7.

Figure 11.7 One of Menaechmus' solutions to the problem of two mean proportionals, as reported by Eutocius.

This solution uses only figures that arise naturally from circles and straight lines, yet people were not satisfied with it. The objection to it was that the data and the resulting figure all lie within a plane, but the construction requires the use of cones, which cannot be contained in the plane.

11.3 Trisecting the Angle

The practicality of trisecting an angle is immediately evident: It is the first step on the way to dividing a circular arc into any number of equal pieces. If a right angle can be divided into n equal pieces, a circle also can be divided into n equal pieces, and hence the regular n-gon can be constructed. Success in constructing the regular pentagon may have stimulated work on such a program. It is possible to construct the regular n-gon using only straight lines and circles for n = 3, 4, 5, 6, 8, 10, but not 7 or 9. The number 7 is awkward, being the only prime between 5 and 10, and one could expect to have difficulty constructing the regular heptagon. Surprisingly, however, the regular heptakaidecagon (17-sided polygon) can be constructed using only compass and straightedge. Since 9 = 3 · 3, it would seem natural to begin by trying to construct this figure, that is, to construct an angle of 40°. That would be equivalent to constructing an angle of 20°, hence trisecting the angles of an equilateral triangle.

Despite the seeming importance of this problem, less has been written about the ancient attempts to solve it than about the other two problems. For most of the history we are indebted to two authors. In his commentary on Euclid's Elements, Proclus mentions the problem and says that it was solved by Nicomedes using his conchoid and by others using the quadratrices of Hippias and Nicomedes (280–210). In Book 4 of his Synagg (Collection), Pappus says that the circle was squared using the curve of Dinostratus and Nicomedes. He then proceeds to describe that curve, which is the one now referred to as the quadratrix of Hippias.³

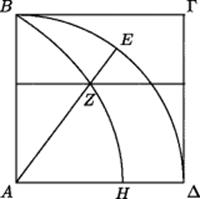
The quadratrix is described in terms of two independent motions of a point as follows. The radius of a circle rotates at a uniform rate from the vertical position AB in Fig. 11.8 to the horizontal position AΔ, while in exactly the same time a horizontal line moves downward at a constant speed from the position BΓ to the position AΔ. The point of intersection Z traces the curve BZH, which is the quadratrix. The diameter of the circle is the mean proportional between its circumference and the line AH. Unfortunately, H is the one point on the quadratrix that is not determined, since the two intersecting lines coincide when they both reach AΔ. This point was noted by Pappus, citing an earlier author named Sporos. In order to draw the curve, which is mechanical, you first have to know the ratio of the circumference of a circle to its diameter. But if you knew that, you would already be able to square the circle. One can easily see, however, that since the angle ZAΔ is proportional to the height of Z, this curve—if it can be drawn!—makes it possible to divide an angle into any number of equal parts.

Figure 11.8 The quadratrix of Hippias.

Pappus also attributed a trisection to Menelaus of Alexandria (70–130 CE). Pappus gave a classification of geometric construction problems in terms of three categories: planar, solid, and [curvi]linear. The first category consisted of constructions that used only straight lines and circles, whereas the second category consisted of those that used conic sections. The last, catch-all category consisted of problems requiring all manner of more elaborate and less regular curves, which were harder to visualize than the first two and presumably required some mechanical device to draw them. We are all familiar with the use of a compass to draw a perfect circle and the procedure for drawing an ellipse by stretching a thread between two pins at the foci. A device for drawing hyperbolas with given foci is also easy to design.4 Somewhat surprisingly, it was not until the nineteenth century that a mechanical device (the Peaucellier linkage, named after Charles-Nicolas Peaucellier, 1832–1914) was invented that draws a theoretically perfect straight line.

The quadratrix described above, however, cannot be drawn with any such instrument; it requires coordinating two independent motions with infinite precision, a thing that is difficult to imagine. Pappus says that some of these more general curves come from locus problems; he goes on to say that geometers regard it as a major defect when a planar problem is solved using conics and other curves.

Based on this classification of problems, the first geometers were unable to solve the abovementioned problem of [trisecting] the angle, which is by nature a solid problem, through planar methods. For they were not yet familiar with the conic sections; and for that reason they were at a loss. But later they trisected the angle through conics, using the convergence described below.

The word convergence (neûsis) comes from the verb neúein, one of whose meanings is to incline toward. In this particular case, it refers to the following construction. We are given a rectangle ABΓΔ and a prescribed length m. It is required to find a point E on ΓΔ such that when AE is drawn and extended to meet the extension of BΓ at a point Z, the line EZ will have length m. The construction is shown in Fig. 11.9, where the circular arc with center at Δ has radius m. The hyperbola is rectangular, with asymptotes BA and BZ, so that AΔ · ΓΔ = ΛH · ZH. This equation implies that ΠZ : HZ = ΠA : ΔA. Thus the triangles ΔΠH and AΠZ are similar, and so AZ is parallel to ΔH, from which it follows that EZ = ΔH = m.

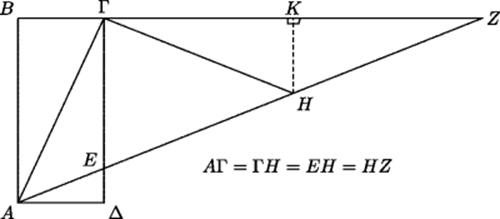
With the neûsis construction, it becomes a simple matter to trisect an angle, as Pappus pointed out. Given any acute angle, label its vertex A, choose an arbitrary point Γ on one of its sides, and let Δ be the foot of the perpendicular from Γ to the other side of the angle. Complete the rectangle ABΓΔ, and carry out the neûsis with m = 2AΓ. Then let H be the midpoint of ZE, and join ΓH, as shown in Fig. 11.10.

Figure 11.9 Pappus' construction of a neÛsis using a rectangular hyperbola.

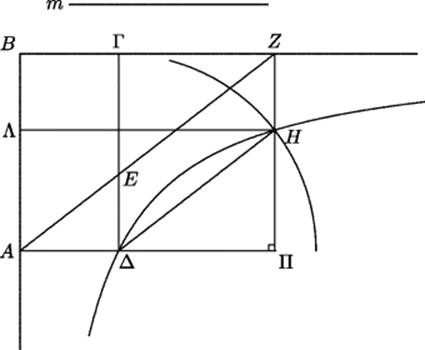
Figure 11.10 Trisection of an arbitrary angle by neûsis construction. Because EH = HZ and both HK and ΓΔ are perpendicular to BZ, it follows that ΓK = KZ. Hence ZKH is congruent to ΓKH, and so ∠HΓK = ∠ HZK = ∠ EAΔ. But then ΓH = HZ = AΓ, and so ∠ΓAH = ∠ ΓHA = 2 ∠ HZΓ.

11.3.1 A Mechanical Solution: The Conchoid

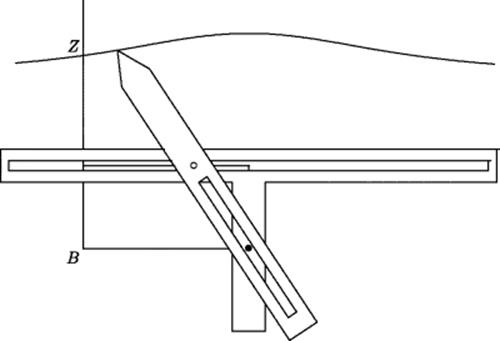
Finding the point E in the neûsis problem is equivalent to finding the point Z. Either point allows the line AEZ to be drawn. Now one line that each of these points lies on is known. If some other curve that Z must lie on could be drawn, the intersection of that curve with the line BΓ would determine Z and hence solve the neûsis problem. If we use the condition that the line ZE must be of length 2AΓ, we have a locus-type condition for Z, and it is easy to build a device that will actually draw this locus. What is needed is the T-shaped frame shown in Fig. 11.11, consisting of two pieces of wood or other material meeting at right angles. The horizontal part of the T has a groove along which a peg (shown as a hollow circle in the figure) can slide. The vertical piece has a fixed peg (shown as a solid circle) at distance AΔ from its top. Onto this frame a third piece is fitted with a fixed peg (the hollow circle) at distance mfrom its end and a groove between the peg and the other end that fits over the peg on the vertical bar. The frame is then laid down with its horizontal groove over the line ΓΔ and its fixed peg over A. When the moving piece is fitted over the frame so that its peg slides along the horizontal groove over ΓΔ and its groove slides over the peg at A, its endpoint (where a stylus is located to draw the curve) traces the locus on which Z must lie. The point Z lies where that locus meets the extension of BΓ. In practical terms, such a device can be built, but the rigid pegs must be located at exactly the distance from the ends determined by the rectangle and the fixed distance given in the neûsisproblem. Thus the device must be modified by moving the pegs to the correct locations for each particular problem. If oxymoron is permitted, we might say that the practical value of this device is mostly theoretical. The locus it draws is the conchoid of Nicomedes, mentioned by Pappus and Proclus. (Nothing is known about Nicomedes beyond the facts that he lived during the third century BCE and wrote a treatise on conchoid curves.)

Figure 11.11 A mechanical device for drawing the conchoid of Nicomedes.

Because of the objections reported by Pappus to the use of methods that were more elaborate than the problems they were intended to solve, the search for planar (ruler-and-compass) solutions to these problems continued for many centuries. It was not until the 1830s that it was proved that no straightedge-and-compass solution exists for any of them. (The proof had no effect on the cranks of the world, of course.) The problems continue to be of interest since that time, and not only to cranks who imagine they have solved them. Felix Klein, a leading German mathematician and educator in the late nineteenth and early twentieth centuries, urged that they be studied as a regular part of the curriculum (Beman and Smith, 1930).

Problems and Questions

Mathematical Problems

11.1 Show why the quantities u, , , and h in Fig. 11.6 satisfy the relation . (Use the second diagram in the figure, which shows that . You will also need the relations and . You need to eliminate using these last two relations.)

11.2 Referring to Fig. 11.5, show that at the intersection of the parabola and hyperbola, where x = B and y = Γ, we have A : B : : B : Γ and A : B : : Γ : E.

11.3 Explain why the point H in Fig. 11.6 is not determined by the conditions given in the definition of the quadratrix.

Historical Questions

11.4 Why did the center of Greek mathematics shift from the commercial cities in the Ionian Sea to Athens during the fifth century BCE ?

11.5 Who were the scholars who came to Athens in fifth and fourth centuries BCE and worked on mathematical problems while they were there?

11.6 Summarize the progress made on each of the three classical problems during the fourth century BCE.

Questions for Reflection

11.7 Try to design a mechanical instrument that will draw a quadratrix for a given circle. (You will need to assume an ideal thread that is perfectly flexible but incapable of being stretched in order to do this.)

11.8 Why is a neûsis not a straightedge-and-compass construction?

11.9 Why was it important to Menaechmus' solution of the problem of two mean proportionals that the plane cutting the cone be at right angles to one of its generators?

Notes

1. Alexander was a man of action, and there is no evidence anywhere in his entire career that Aristotle had had the slightest influence on him. He was also apparently tutored by Menaechmus (ca. 380–ca. 320), another student of Plato. The fifth-century CE writer Stobaeus writes that Alexander insisted on getting an abridged course in geometry, but Menaechmus told him there were no “kingshighways” in geometry and that everyone had to follow the same road. (Stobaeus, Book 2, Chapt. 31, SS115. Proclus tells the same story with Ptolemy Soter in place of Alexander and Euclid in place of Menaechmus.)

2. Plagues were apparently common in ancient Greece. One is described at the outset of Homer's Iliad as being due to the wrath of Apollo. Another occurs in Sophocles' Oedipus the King, and another decimated Athens early in the Peloponnesian War, claiming Pericles as one of its victims.

3. Hippias should be thankful for Proclus, without whom he would apparently be completely forgotten, as none of the other commentators discuss him, except for a mention in passing by Diogenes Laertius in his discussion of Thales. Allman (1889, pp. 94–95) argued that the Hippias mentioned in connection with the quadratrix is not the Hippias of Elis (ca. 460–ca. 400 BCE) mentioned in the Eudemian summary, and other historians, including the late Wilbur Knorr, have agreed with him, but most do not.

4. Imagine two spools with meshing gears on axes beneath the plane of the hyperbola, with a continuous thread wound around them in opposite directions and passing up over the table through the two foci. As a point on the thread is pulled, the two interlocked spools will both unwind at the same rate, keeping the difference between the lengths of thread from the given point to the two foci constant. Hence the point will describe a hyperbola.