The history of mathematics: A brief course (2013)

Part III. Greek Mathematics From 500 BCE to 500 CE

Chapter 12. Athenian Mathematics II: Plato and Aristotle

As we have already mentioned, Plato met the Pythagorean Philolaus in Sicily in 390. He also met the Pythagorean Archytas at Tarentum, where some Pythagoreans had once fled to escape danger at Croton. Plato returned to Athens and founded the Academy in 387 BCE. There he hoped to train the young men¹ for public service and establish good government. At the behest of Archytas and a Syracusan politician named Dion, brother-in-law of the ruler Dionysus I, Plato made several trips to Syracuse (Sicily) between 367 and 361 BCE to act as advisor to Dionysus II. However, there was virtual civil war between Dion and Dionysus, and Plato was arrested and nearly executed. Diogenes Laertius quotes a letter allegedly from Archytas to Dionysus urging that Plato be released. Plato returned to the Academy in 360 and remained there for the last 13 years of his life. He died in 347.

12.1 The Influence of Plato

Archytas' solution of the problem of two mean proportionals using two half-cylinders intersecting at right angles was mentioned above. In his Symposium Discourses, Plutarch claimed that Plato also lamented that the disciples of Eudoxus, Archytas, and Menaechmus attacked the duplication of a solid by building tools and machinery hoping to get two ratios through the irrational, by which it might be possible to succeed, [saying that by doing so they] immediately ruined and destroyed the good of geometry by turning it back toward the physical and not directing it upward or striving for the eternal and incorporeal images, in which the divinity is eternally divine. Although the sentiment Plutarch ascribes to Plato is consistent with the ideals expressed in the Republic, Eutocius reports one such mechanical construction as being due to Plato himself. From his upbringing as a member of the Athenian elite and from the influence of Socrates, Plato had a strong practical streak, concerned with life as it is actually lived.² Platonic idealism in the purely philosophical sense does not involve idealism in the sense of unrealistic striving for perfection. It may have been Archytas and Philolaus who aroused Plato's interest in mathematics, an interest that continued for the rest of his life. Mathematics played an important role in the curriculum of his Academy and in the research conducted there. Lasserre (1964, p. 17) believes that the most important mathematical work at the Academy began with the arrival of Theaetetus in Athens around 375 and ended with Eudoxus' departure for Cnidus around 350. The principle that knowledge can involve only eternal, unchanging entities led Plato to some statements that sound paradoxical. For example, in Book 7 of the Republic he writes:

Thus we must make use of techniques such as geometry when we take up astronomy and ignore what is in the sky if we really intend to create something intrinsically useful and practical in the soul.

If Plato's mathematical concerns seem to be largely geometrical, that is probably because he became acquainted with mathematics at the time when the challenges discussed above were still current topics. (Recall the quotation from the Republic in Chapter 8, where he laments the lack of public support for research into solid geometry.) There is a long-standing legend that Plato's Academy bore the following sign above its entrance³:

AΓEΩMETPHTOΣ MHΔEIΣ EIΣITΩ

(AGEMETRTOS MDEIS EISIT, that is,“Let no one unskilled in geometry enter.”) If Plato really was more concerned with geometry than with arithmetic, there is an obvious explanation for his preference: The imperfections of the real world come more from geometry than arithmetic. For example, it is sometimes asserted that there are no examples of exact equality in the real world. But in fact, as was pointed out in Chapter 1, there are many. Those who make the assertion always have in mind continuous magnitudes, such as lengths or weights, in other words, geometrical concepts. Where arithmetic is concerned, exact equality is easy to achieve, as shown by the example of equal bank accounts in Chapter 1. But Plato's love for geometry should not be overemphasized. In his ideal curriculum, described in the Republic, arithmetic is still regarded as the primary subject.

12.2 Eudoxan Geometry

We recall the difficulty occasioned for the theory of proportion by the discovery of incommensurables, as illustrated by Fig 12.4 of Chapter 10. The solution to this difficulty was provided by Eudoxus of Cnidus (ca. 407–354 BCE), whom Diogenes Laertius describes as “astronomer, geometer, physician, and lawgiver.” He learned geometry from Archytas and philosophy from Plato. Diogenes Laertius cites another commentator, named Sotion, who said that Eudoxus spent two months in Athens and attended lectures by Plato. Because of his poverty, he could not afford to live in Athens proper. He lived at the waterfront, known as the Piraeus, supported by a physician named Theomedus, and walked 11 km from there into Athens. Then, with a subsidy from friends, he went to Egypt and other places and finally returned, “crammed full of knowledge,” to Athens, “some say, just to annoy Plato for snubbing him earlier.” Plato was not in Eudoxus' league as a mathematician; and if Eudoxus felt that Plato had patronized him in his earlier visit, perhaps because Plato and his other students were wealthy and Eudoxus was poor, his desire to return and get his own students back from Plato is quite understandable. He must have made an impression on Plato on his second visit. In his essay On Socrates' Daemon, Plutarch reports that when the Delians consulted Plato about doubling the cube, in addition to advising them to study geometry, he told them that the problem had already been solved by Eudoxus of Cnidus and Helicon of Cyzicus. If true, this story suggests that the Delians appealed to Plato after Eudoxus had left for Cnidus, around 350. In Cnidus, Eudoxus made many astronomical observations that were cited by the astronomer Hipparchus (ca. 190–ca. 120 BCE), and one set of his astronomical observations has been preserved. Although the evidence is not conclusive, it seems that while he was in Athens, he contributed two vital pieces to the mosaic that is Euclid's Elements.

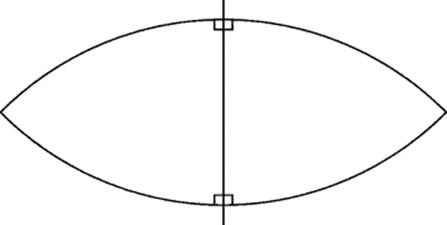
Figure 12.4 How do we exclude the possibility that two lines perpendicular to the same line may intersect each other?

12.2.1 The Eudoxan Definition of Proportion

The first piece of the Elements probably contributed by Eudoxus was the solution of the problem of incommensurables. This solution is attributed to him on the basis of two facts: (1) Proclus' comment that Euclid “arranged many of the theorems of Eudoxus”; (2) an anonymous scholium (commentary) on Euclid's Book 5, which asserts that the book is the creation “of a certain Eudoxus, [the student] of the teacher Plato” (Allman, 1889, p. 132).

The main principle is very simple: Suppose that D and S are, respectively, the diagonal and side of a square or pentagon. Even though there are no integers m and n such that mD = nS, so that the ratio D : S cannot be defined as n : m for any integers, it remains true that for every pair of integers m and n there is a trichotomy: Either mD < nS or mD = nS or mD > nS. That fact makes it possible at least to define what is meant by saying that the ratio of D to S is the same for all similar polygons. We define the proportion D₁ : S₁ : : D₂ : S₂ for two different squares to mean that, for any positive integers m and n, whatever relation holds between mD₁ and nS₁ also holds between mD₂ and nS₂. That is, if mD₁ > nS₁, then mD₂ > nS₂, and similarly for the opposite inequality or equality.

As defined by Euclid at the beginning of Book 5, “A relation that two magnitudes of the same kind have due to their sizes is a ratio.” As a definition, this statement is somewhat lacking, but we may paraphrase it as follows: “the relative size of one magnitude in terms of a second magnitude of the same kind is the ratio of the first to the second.” We think of size as resulting from measurement and relative size as the result of dividing one measurement by another, but Euclid keeps silent on both of these points. Then, “Two magnitudes are said to have a ratio to each other if they are capable of exceeding each other when multiplied.” That is, some (positive integer) multiple of each is larger than the other. Thus, the periphery of a circle and its diameter have a ratio, but the periphery of a circle and the disk it encloses do not. Although this definition of ratio would be hard to use, fortunately there is no need to use it. What is needed is equality of ratios, that is, proportion. That definition follows from the trichotomy just mentioned. Here is the definition given in Book 5 of Euclid, with the material in brackets added from the discussion just given to clarify the meaning:

Magnitudes are said to be in the same ratio, the first to the second [D₁ : S₁] and the third to the fourth [D₂ : S₂], when, if any equimultiples whatever be taken of the first and third [mD₁ and mD₂] and any equimultiples whatever of the second and fourth [nS₁ and nS₂], the former equimultiples alike exceed, are alike equal to, or are alike less than the latter equimultiples taken in corresponding order [that is, mD₁ > nS₁ and mD₂ > nS₂, or mD₁ = nS₁ and mD₂ = nS₂, or mD₁ < nS₁ and mD₂ < nS₂].

Let us now revisit our conjectured early proof of Euclid's Proposition 1 of Book 6 of the Elements from Chapter 10, a proof that holds only in the commensurable case. How much change is required to make this proof cover the incommensurable case? Very little, as it turns out. Where we have assumed that 3BC = 2CD, it is only necessary to consider the cases 3BC > 2CD and 3BC < 2CD and show with the same figure that 3ABC > 2ACD and 3ABC < 2ACD, respectively, and that is done by using the trivial corollary of Proposition 38 of Book 1: If two triangles have equal altitudes and unequal bases, the one with the larger base is larger. Eudoxus has not only shown how proportion can be defined so as to apply to incommensurables, he has done so in a way that fits together seamlessly with earlier proofs that apply only to the commensurable case. If only the fixes for bugs in modern computer programs were so simple and effective!

12.2.2 The Method of Exhaustion

Eudoxus' second contribution is of equal importance with the first; it is the proof technique known as the method of exhaustion. This method is used by both Euclid and Archimedes to establish theorems about areas and solids bounded by curved lines and surfaces. As in the case of the definition of proportion for incommensurable magnitudes, the evidence that Eudoxus deserves the credit for this technique is not conclusive. In his commentary on Aristotle's Physics, Simplicius credits the Sophist Antiphon with inscribing a polygon in a circle, then repeatedly doubling the number of sides in order to square the circle. However, the perfected method seems to belong to Eudoxus. Archimedes says in the cover letter accompanying his treatise on the sphere and cylinder that it was Eudoxus who proved that a pyramid is one-third of a prism on the same base with the same altitude and that a cone is one-third of the cylinder on the same base with the same altitude. What Archimedes meant by proof we know: He meant proof that meets Euclidean standards. Such a proof can be achieved for the cone only by the method of exhaustion. Like the definition of proportion, the basis of the method of exhaustion is a simple observation: When the number of sides of a polygon inscribed in a circle is doubled, the excess of the circle over the polygon is reduced by more than half, as one can easily see from Fig. 12.1. This observation works together with the theorem that if two magnitudes have a ratio and more than half of the larger is removed, then more than half of what remains is removed, and this process continues, then at some point what remains will be less than the smaller of the original two magnitudes (Elements, Book 10, Proposition 1). This principle is usually called Archimedes' principle because of the frequent use he made of it. The phrase if two magnitudes have a ratio is critical, because Euclid's proof of the principle depends on converting the problem to a problem about integers.

Figure 12.1 The basis of the method of exhaustion.

To be specific, if a > b, since nb > a for some positive integer n, it is only a matter of showing that a finite sequence a = a₁, a₂, . . . in which each term is less than half of the preceding will eventually reach a term a_k such that na_kis less than a₁. Since nb > a = a₁, it follows that a_k < b. Since m/2^m < 1 for m > 1, we see that in fact k will be less than or equal to n.

The definition of ratio and proportion allowed Eudoxus/Euclid to establish all the standard facts about the theory of proportion, including the important fact that similar polygons are proportional to the squares on their sides (Elements, Book 6, Propositions 19 and 20). Once that result is achieved, the method of exhaustion makes it possible to establish rigorously that similar curvilinear regions are proportional to the squares on similarly situated chords. In particular, it made it possible to prove the fundamental fact that was being used by Hippocrates much earlier: Circles are proportional to the squares on their diameters. This fact is now stated as Proposition 2 of Book 12 of the Elements, and the proof given by Euclid is illustrated in Fig. 12.2.

Figure 12.2 Proof that circles are proportional to the squares on their diameters.

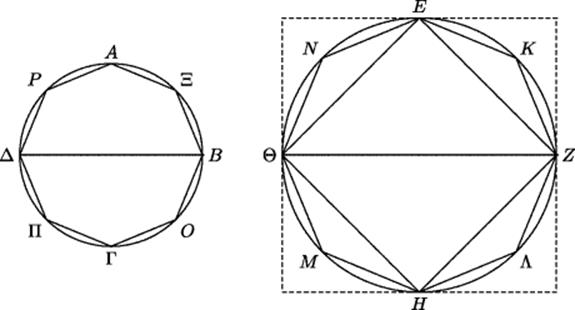
Let ABΓΔ and EZHΘ be two circles with diameters BΔ and ΘZ, and suppose that the circles are not proportional to the squares on their diameters. Let the ratio BΔ² : ΘZ² be the same as ABΓΔ : Σ, where Σ is an area larger or smaller than EZHΘ. Suppose first that Σ is smaller than the circle EZHΘ. Draw the square EZHΘ inscribed in the circle EZHΘ. Since this square is half of the circumscribed square with sides perpendicular and parallel to the diameter ΘZ, and the circle is smaller than the circumscribed square, the inscribed square is more than half of the circle. Now bisect each of the arcs EZ, ZH, HΘ, and ΘE at points K, Λ, M, and N, and join the polygon EKZΛHΘNE. As shown above, doing so produces a larger polygon, and the excess of the circle over this polygon is less than half of its excess over the inscribed square. If this process is continued enough times, the excess of the circle over the polygon will eventually be less than its excess over Σ, and therefore the polygon will be larger than Σ. For definiteness, Euclid assumes that this polygon is the one reached at the first doubling: EKZΛHΘNE. In the first circle ABΓΔ, inscribe a polygon AΞBOΓΠΔP similar to EKZΛHΘNE. Now the square on BΔ is to the square on ZΘ as AΞBOΓΠΔP is to EKZΛHΘNE. But also the square on BΔ is to the square on ZΘ as the circle ABΓΔ is to Σ. It follows that AΞBOΓΠΔP is to EKZΛHΘNE as the circle ABΓΔ is to Σ. Since the circle ABΓΔ is larger than AΞBOΓΠΔP, it follows that Σ must be larger than EKZΛHΘNE, But by construction, it is smaller, which is impossible. A similar argument shows that it is impossible for Σ to be larger than EZHΘ.

12.2.3 Ratios in Greek Geometry

Ratios as defined by Euclid are always between two magnitudes of the same type. He never considered what we call density, for example, which is the ratio of a mass to a volume. Being always between two magnitudes of the same type, ratios are “dimensionless” in our terms and could be used as numbers, if only they could be added and multiplied. The Greeks, however, did not think of these operations on ratios as being the same thing they could do with numbers. In terms of adding, Euclid does say (Book 6, Proposition 24) that if two proportions have the same second and fourth terms, then their first terms and third terms can be added (first to first and third to third), that is, if a : b : : c : d and e : b : : f : d, then (a + e) : b : : (c + f) : d. But he did not think of the second and fourth terms in a proportion as denominators, and this was not, as we see it, merely adding fractions with a common denominator. For multiplication of ratios, Euclid gives three separate definitions. In Book 5, Definition 9, he defines the duplicate (which we would call the square) of the ratio a : b to be the ratio a : c if b is the mean proportional between a and c, that is, a : b : : b : c. Similarly, when there are four terms in proportion, as in the problem of two mean proportionals, so that a : b : : b : c : : c : d, he calls the ratio a : d the triplicate of a : b. We would call it the cube of this ratio. Not until Book 6, Definition 5 is there any kind of general definition of the product of two ratios. Even that definition is not in all manuscripts and may be a later interpolation. It goes as follows: A ratio is said to be the composite of two ratios when the sizes in the two ratios produce something when multiplied by themselves.⁴ This rather vague definition is made still harder to grasp by the fact that the word for composite (sygkeímena) is simply a general word for combined. It means literally lying together and is the same word used when two lines are placed end to end to form a longer line. In that context it corresponds to addition, whereas in the present one it corresponds to multiplication. It can be understood only by seeing the way that Euclid operates with it. Given four lines a, b, c, and d, to form the composite ratio a : b . c : d, Euclid first takes any two lines⁵ x and y such that a : b : : x : y. He then finds a line zsuch that y : z : : c : d and defines the composite ratio a : b . c : d to be the ratio x : z.

There is some arbitrariness in this procedure, since x could be any line. A modern mathematician looking at this proof would note that Euclid could have shortened the labor by taking x = a and y = b, then constructing z to have the same ratio to y that d has to c. The same mathematician would add that Euclid ought to have shown that the final ratio is the same independently of the choice of x, which he did not do. But one must remember that the scholarly community around Euclid was much more intimate than in today's world; he did not have to write a “self-contained” book. In the present instance a glance at Euclid's Data shows that he knew what he was doing. The first proposition in that book says that “if two magnitudes [of the same kind] A and B are given, then their ratio is given.” In modern language, any quantity can be replaced by an equal quantity in a ratio without changing the ratio. The proof is that if A = Γ and B = Δ, then A : Γ : : B : Δ, and hence by Proposition 16 of Book 5 of the Elements, A : B : : Γ : Δ. The second proposition of the Data draws the corollary that if a given magnitude has a given ratio to a second magnitude, then the second magnitude is also given. That is, if two quantities have the same ratio to a given quantity, then they are equal. From these principles, Euclid could see that the final ratio x : z is what mathematicians now call “well-defined,” that is, independent of the choice of x.⁶ The first use made of this process is in Proposition 23 of Book 6, which asserts that equiangular parallelograms are in the compound ratio of their (corresponding) sides.

With the departure of Eudoxus for Cnidus, we can bring to a close our discussion of Plato's influence on mathematics. If relations between Plato and Eudoxus were less than intimate, as Diogenes Laertius implies, Eudoxus may have drawn off some of Plato's students whose interests were more scientific (in modern terms) and less philosophical. It is likely that even Plato realized that his attempt to explain the universe by means of eternal ideal forms, for the understanding of which mathematics was a useful training tool, would not work after all. His late dialogue Parmenides gives evidence of a serious rethinking of this doctrine.

12.3 Aristotle

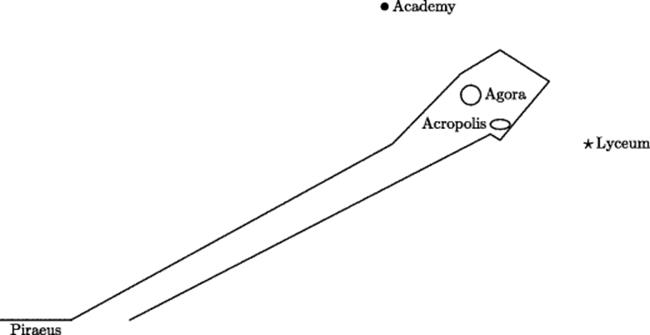
Plato died in 347 BCE, and his place as the preeminent scholar of Athens was taken a decade after his death by his former pupil Aristotle (384–322 BCE). Aristotle became a student at the Academy at the age of 18 and remained there for 20 years. After the death of Plato he left Athens, traveled, got married, and in 343 became tutor to the future Macedonian King Alexander (the Great), who was 13 years old when Aristotle began to teach him and 16 when he became king on the death of his father. In 335 Aristotle set up his own school, located in the Lyceum, over the hill from the Academy (Fig 12.3).⁷ For the next 12 years he lived and wrote there, producing an enormous volume of speculation on a wide variety of subjects, scientific, literary, and philosophical. In 322 Alexander died, and the Athenians he had conquered turned against his friends. Unlike Socrates, Aristotle felt no obligation to be a martyr to the laws of the polis. He fled to escape the persecution, but died the following year. Aristotle's writing style resembles very much that of a modern scholar, except for the absence of footnotes. Like Plato, in mathematics he seems more like a well-informed generalist than a specialist.

Figure 12.3 Athens in the fourth century BCE: the waterfront (Piraeus), Academy, and Lyceum.

The drive toward the logical organization of science reached its full extent in the treatises of Aristotle. He analyzed reason itself and gave a rigorous discussion of formal inference and the validity of various kinds of arguments in his treatise Prior Analytics, which was written near the end of his time at the Academy, around 350 BCE. One can almost picture debates at the Academy, with the mathematicians providing examples of their reasoning, which the logician Aristotle examined and criticized in order to distill his rules for making inferences. In this treatise Aristotle discusses subjects, predicates, and syllogisms connecting the two, occasionally giving a glimpse of some mathematics that may indicate what the mathematicians were doing at the time.

In Book 1 of the Prior Analytics, Aristotle describes how to organize the study of a subject, looking for all the attributes and subjects of both of the terms that are to appear in a syllogism. The subject–attribute relation is mirrored in modern thought by the notion of elements belonging to a set. The element is the subject, and the set it belongs to is defined by attributes that can be predicated of all of its elements and no others. Just as sets can be elements of other sets, Aristotle said that the same object can be both a subject and a predicate. He thought, however, that there were some absolute subjects (individual people, for example) that were not predicates of anything and some absolute predicates (what we call abstractions, such as beauty) that were never the subject of any proposition.⁸ Aristotle says that the postulates appropriate to each subject must come from experience. If we are thorough enough in stating all the attributes of the fundamental terms in a subject, it will be possible to prove certain things and state clearly what must be assumed.

In Book 2 he discusses ways in which reasoning can go wrong, including the familiar fallacy of “begging the question” by assuming what is to be proved. In this context he offers as an example the people who claim to construct parallel lines. According to him, they are begging the question, starting from premises that cannot be proved without the assumption that parallel lines exist. We may infer that there were around him people who did claim to show how to construct parallel lines, but that he was not convinced. It seems obvious that two lines perpendicular to the same line are parallel, but surely that fact, so obvious to us, would also be obvious to Aristotle. Therefore, he must have looked beyond the obvious and realized that the existence of parallel lines does not follow from the immediate properties of lines, circles, and angles. Only when this realization dawns is it possible to see the fallacy in what appears to be common sense. Common sense—that is, human intuition—suggests what can be proved: If two perpendiculars to the same line meet on one side of the line, then they must meet on the other side also, as in Fig. 12.4. Indeed, Ptolemy did prove this, according to Proclus. But Ptolemy then concluded that two lines perpendicular to the same line cannot meet at all. “But,” Aristotle would have objected, “you have not proved that two lines cannot meet in two different points.” And he would have been right: The assumptions that two lines can meet in only one point and that the two sides of a line are different regions (not connected to each other) are equivalent to assuming that parallel lines exist.

Euclid deals with this issue in the Elements by stating as the last of his assumptions that “two straight lines do not enclose an area.” Oddly, however, he seems unaware of the need for this assumption when proving the main lemma (Book 1, Proposition 16) needed to prove the existence of parallel lines.⁹ This proposition asserts that an exterior angle of a triangle is larger than either of the opposite interior angles. Euclid's proof is based on Fig. 12.5, in which a triangle ABΓ is given with side BΓ extended to Δ, forming the exterior angle AΓΔ. He wishes to prove that this angle is larger than the angle at A. To do so, he bisects AΓ at E, draws AE, and extends it to Z so that EZ = AE. When ZΓ is joined, it is seen that the triangles ABE and ΓZE are congruent by the side–angle–side criterion. It follows that the angle at A equals ∠EΓZ, which is smaller than ∠EΓΔ, being only a part of it.

Figure 12.5 The exterior angle theorem (Elements, I, 16).

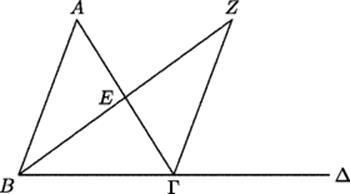
In the proof, Euclid assumes that the points E and Z are on the same side of line BΓ. But that is obvious only for triangles small enough to see. It needs to be proved. To be sure, Euclid could have proved it by arguing that if E and Z were on opposite sides of BΓ, then EZ would have to intersect either BΓ or its extension in some point H, and then the line BH passing through Γ and the line BEH would enclose an area. But he did not do that. In fact, the only place where Euclid invokes the assumption that two lines cannot enclose an area is in the proof of the side–angle–side criterion for congruence (Book 1, Proposition 4).¹⁰

Granting that Aristotle was right about this point, we still must wonder why he considered the existence of parallel lines to be in need of proof. Why would he have doubts about something that is so clear on an intuitive level? One possible reason is that parallelism involves the infinite: Parallel lines will never meet, no matter how far they are extended. If geometry is interpreted physically (say, by regarding a straight line as the path of a light ray), we really have no assurance whatever that parallel lines exist—how could anyone assert with confidence what will happen if two apparently parallel lines are extended to a length of hundreds of light years?

As Aristotle's discussion of begging the question continues, further evidence comes to light that this matter of parallel lines was being debated around 350, and proofs of the existence of parallel lines (Book 1, Proposition 27 of the Elements) were being proposed, based on the exterior-angle principle. In pointing out that different false assumptions may lead to the same wrong conclusion, Aristotle notes in particular that the nonexistence of parallel lines would follow if an internal angle of a triangle could be greater than an external angle (not adjacent to it), and also if the angles of a triangle added to more than two right angles.¹¹ One is almost tempted to say that the mathematicians who analyzed the matter in this way foresaw the non-Euclidean geometry of Riemann, but of course that could not be. Those mathematicians were examining what must be assumed in order to get parallel lines into their geometry. They were not exploring a geometry without parallel lines.

It is precisely in the matter of the parallel postulate—equivalent to the angle sum of a triangle being two right angles—that we see the extent to which geometry was still partly an intuitive science, not merely a matter of verbal deduction from premises. Nowadays we take it for granted that formal systems begin with undefined terms and axioms and proceed to deduce theorems. As far as mathematics is concerned, the undefined terms have no interpretation. But for centuries they did have interpretation, and Aristotle shows what it was in a passage from his Physics (Bekker, 200a).

There are closely similar inevitable paths both in mathematics and in the natural world. For if the three sides [of a triangle] are straight lines, then [the sum of the angles of] the triangle is two right [angles]; and if the latter holds, so does the former. But if the latter does not hold, then the lines are not straight.

This passage gives a hint that Aristotle knew about the angles of spherical triangles and knew that they added up to more than two right angles. Thus, although we can interpret the word line to mean a great circle on a sphere, Aristotle could not, since a line was not merely an undefined term for him.

Problems and Questions

Mathematical Problems

12.1 How would you establish that two triangles with equal altitudes and equal bases are equal (“in area,” as we would say, although Euclid would not)?

12.2 Rephrase Hippocrates' quadrature of the lune shown in Fig 12.1 of Chapter 11 in terms of proportions between figures and the squares on parts of their boundaries. (In other words “de-algebraize” the argument given in the text of the preceding chapter.)

12.3 Consider two rectangles R with sides a and b and S with sides c and d. Prove that the ratio R : S is the composite of the two ratios a : c and b : d. [Hint: Assume given three quantities x, y, and z such that a : c : : x : y and b : d : : y : z. You need to prove that R : S : : x : z. To that end, let m and n be any positive integers such that mx > nz. You now need to prove that mR > nS. In order to do that, choose an integer p so large that p(mx − nz) > y. Then there is an integer q such that pmx > qy > pnz. (Why?) It follows from the proportions that pma > qc and qb > pnd. Hence the rectangle with sides pma and qb is larger than the rectangle with sides qc and pnd. Show how to conclude from that result that mR > nS.]

Historical Questions

12.4 In what important ways, in addition to the logical arrangement of materials and the insistence on strict proof, does Greek mathematics differ from the mathematics of Mesopotamia and Egypt?

12.5 Why did Plato regard the study of mathematics as important for those who were to be the guardians of his ideal state?

12.6 Why is the problem of squaring the circle much more difficult than the problem of doubling the cube or trisecting the angle?

Questions for Reflection

12.7 Why was the problem of incommensurables a genuine difficulty that needed to be overcome, while the paradoxes of Zeno and the classical construction problems were not?

12.8 It appears that the Greeks overlooked a simple point that might have led them to break out of the confining circle of Euclidean methods. If only they had realized that composite ratios represent multiplication, they would have been freed from the need for dimensional consistency, since their ratios were dimensionless. They could, for example, multiply any number of ratios, whereas interpreting the product of two lines as a rectangle precluded the possibility of any geometric interpretation of product containing more than three factors. Could they have developed analytic geometry if they had made this realization? What else would they have needed?

12.9 Granting that if two lines perpendicular to the same transversal line meet on one side of that line, reflection about the midpoint of the interval between the two points where the lines meet the transversal shows that they must also meet on the other side. How do you know that these two points of intersection are not the same point? What other assumption must you introduce in order to establish that they are different?

Notes

1. In his writing, especially The Republic, Plato argues for equal participation by women in government. There is no record of any women students at his Academy, however. His principles were far in advance of what the Athenians would tolerate in practice.

2. In the famous allegory of the cave in Book 7 of the Republic, Plato depicts the unphilosophical person as living in a cave with feet in chains, seeing only flickering shadows on the wall of the cave, while the philosopher is the person who has stepped out of the cave into the bright sunshine and wishes to communicate that reality to the people back in the cave. While he encouraged his followers to “think outside the cave,” his trips to Syracuse show that he understood the need to make philosophy work inside the cave, where everyday life was going on.

3. These words are the earliest version of the legend, which Fowler (1998, pp. 200–201) found could not be traced back earlier than a scholium attributed to the fourth-century orator Sopatros. The commonest source cited for this legend is the twelfth-century Byzantine Johannes Tzetzes, in whose Chiliades, VIII, 975, one finds Mηδε`ιςα´γεωμ´ετρητoςε´ισ´ιτωμoυτ`ηνστ´εγην. “Let no one unskilled in geometry enter my house.”

4. I am aware that the word “in” here is not a literal translation, since the Greek has the genitive case—the sizes of the two ratios. But I take of here to mean belonging to, which is one of the meanings of the genitive case.

5. Actually, m and n need not be lines as long as they “have a ratio,” that is, are geometric objects of the same kind. The exact nature of x, y, and z is not important, since in applications only the integers by which they are multiplied play any role in the argument.

6. A good exposition of the purpose of Euclid's Data and its relation to the Elements was given by Il'ina (2002), elaborating a thesis of I. G. Bashmakova.

7. The names of these two institutions have become a basic part of our intellectual world, masking their origins. Both are named for their geographical location in Athens. The Academy was a wooded area named in honor of Akademos, who, according to legend, saved Athens from the wrath of Castor and Pollux by telling them where the Athenian king Theseus had hidden their sister Helen. The Lyceum was located near the temple of Apollo Lykeios (“Apollo of the Wolves”).

8. In modern set theory it is necessary to assume that one cannot form an infinite chain of sets a, b, c,. . .such that b a, c b,. . .. That is, at some finite stage in such a chain of element relations, there is an “atom” that has no elements, what is called the empty set.

9. In standard editions of Euclid, there are 14 assumptions, but three of them, concerned with adding equals to equals, doubling equals, and halving equals, are not found in some manuscripts. Gray (1989, p. 46) notes that the fourteenth assumption may be an interpolation by the Muslim mathematician al-Nayrizi, (ca. 875–ca. 940) the result of speculation on the foundations of geometry. That would explain its absence from the proof of Proposition 16.

10. This proof also uses some terms and some hidden assumptions that are visually obvious but which mathematicians nowadays insist on making explicit.

11. Field and Gray (1987, p. 64) note that this point has been made by many authors since Aristotle.