The history of mathematics: A brief course (2013)

Part III. Greek Mathematics From 500 BCE to 500 CE

Chapter 14. Archimedes of Syracuse

Archimedes is one of a small number of mathematicians of antiquity of whose works we know more than a few fragments and of whose life we know more than the approximate time and place. The man indirectly responsible for his death, the Roman general Marcellus, is also indirectly responsible for the preservation of some of what we know about him. Archimedes lived in the Greek city of Syracuse, the name the Greeks seem to have used for the whole island of Sicily on which the city is located, during the third century BCE and is said by Plutarch to have been “a relative and a friend” of King Hieron II. Since Sicily lies nearly on a direct line between Carthage and Rome, it became embroiled in the Second Punic War (218–201 BCE). Marcellus took the city of Syracuse after a long siege, and Archimedes was killed by a Roman soldier in the chaos of the final fall of the city. In the course of writing a biography of Marcellus, Plutarch included some information on Archimedes.

According to Plutarch's biography of Marcellus, the general was very upset that Archimedes had been killed and had his body buried in a suitably imposing tomb. When a nation is conquered, it often happens that the conquerors are insufficiently appreciative of its cultural achievements and the conquered nation is unable to preserve the relics of that culture. Such was the case with Archimedes. According to Eutocius, a biography of Archimedes was written by a certain Heracleides, who is mentioned in some of Archimedes' letters. However, no copy of this biography is known to exist today. A century after Archimedes' death, his tomb had fallen into neglect. In his Tusculan Disputations, written in 45 BCE, the famous Roman orator and statesman Cicero recalled his discovery of this tomb in 76 BCE.

When I was quaestor I tracked out [Archimedes'] grave, which was unknown to the Syracusans (as they totally denied its existence), and found it enclosed all round and covered with brambles and thickets; for I remembered certain doggerel lines inscribed, as I had heard, upon his tomb, which stated that a sphere along with a cylinder had been set up on the top of his grave. . .Slaves were sent in with sickles who cleared the ground of obstacles. . .So you see, one of the most famous cities of Greece. . . would have been ignorant of the tomb of its one most ingenious citizen, had not a man of Arpinum pointed it out.

During the Middle Ages, the tomb of Archimedes was lost again. In popular tradition, several tombs were erroneously believed to belong to Archimedes. However, the actual tomb may have been rediscovered in 1957, during an excavation.¹ Since Syracuse was taken in 212 BCE and Archimedes was reported by the twelfth-century Byzantine writer Johannes Tzetzes to have been 75 years old at the time of his death, his dates are generally given as 287–212.

There are many legends connected with Archimedes, scattered among the various sources. Plutarch, for instance, says that Archimedes made many mechanical contrivances but generally despised such work in comparison with pure mathematical thought. Plutarch also reports three different stories of the death of Archimedes and tells us that Archimedes wished to have a sphere inscribed in a cylinder carved on his tombstone. The famous story that Archimedes ran naked through the streets shouting “Eureka!” (“I've got it!”) when he discovered the principle of specific gravity in the baths is reported by the Roman architect Vitruvius. Proclus gives another well-known anecdote: that Archimedes built a system of pulleys that enabled him (or King Hieron) single-handedly to pull a ship through the water. Finally, Plutarch and Pappus both quote Archimedes as saying in connection with his discovery of the principle of the lever that if there were another earth, he could move this one by standing on it .

14.1 The Works of Archimedes

With Archimedes we encounter the first author of a considerable body of original mathematical research that has been preserved to the present day. He was one of the most versatile, profound, creative, imaginative, rigorous, and influential mathematicians who ever lived. Ten of Archimedes' treatises have come down to the present, along with a Book of Lemmas that seems to be Archimedean. Some of these works are prefaced by a “cover letter” intended to explain their contents to the person to whom Archimedes sent them. These correspondents of Archimedes were: Gelon, son of Hieron II and one of the kings of Syracuse during Archimedes' life; Dositheus, a student of Archimedes' student and close friend Conon; and Eratosthenes. Like the manuscripts of Euclid, all of the Archimedean manuscripts date from the ninth century or later. These manuscripts have been translated into English and published by various authors. A complete set of Medieval manuscripts of Archimedes' work has been published by Marshall Clagett in the University of Wisconsin series on Medieval Science. In 1998, a palimpsest² of Archimedes' work was sold at auction for $2 million.

The 10 treatises referred to above are the following.

1. On the Equilibrium of Planes, Part I

2. Quadrature of the Parabola

3. On the Equilibrium of Planes, Part II

4. On the Sphere and the Cylinder, Parts I and II

5. On Spirals

6. On Conoids and Spheroids

7. On Floating Bodies

8. Measurement of a Circle

9. The Sand-reckoner

10. The Method

References by Archimedes himself and other mathematicians tell of the existence of other works by Archimedes, of which no manuscripts are now known to exist. These include works on the theory of balances and levers, optics, the regular polyhedra, the calendar, and the construction of mechanical representations of the motion of heavenly bodies.

From this list we can see the versatility of Archimedes. His treatises on the equilibrium of planes and floating bodies contain principles that are now fundamental in mechanics and hydrostatics. The works on the quadrature of the parabola, conoids, and spheroids, the measurement of the circle, and the sphere and cylinder extend the theory of proportion, area, and volume found in Euclid for polyhedra and polygons to the more complicated figures bounded by curved lines and surfaces. The work on spirals introduces a new class of curves, and it develops the theory of length, area, and proportion for them.

Since we do not have space to discuss all of Archimedes' geometry, we shall confine the details of our discussion to what may be his greatest achievements: finding a planar region equal to the surface of a sphere and a polygonal region equal to a segment of a parabola. In addition, because of its impact on the issues involving proof that we have been discussing, we shall discuss his Method and show how he used it to discover certain results on quadrature.

14.2 The Surface of a Sphere

Archimedes' two works on the sphere and cylinder were sent to Dositheus. In the letter accompanying the first of these, he gives some of the history of the problem. Archimedes considered his results on the sphere to be rigorously established, but he did have one regret. He wished he could have published them before Conon's death, “for he is the one we regard as most capable of understanding and rendering a proper judgment on them.”

Archimedes sought a plane surface equal to the surface of a sphere by looking at a “hybrid figure,” which curves in only one direction. (A sphere curves in every direction.) Specifically, he looked at the lateral surface of a frustum of a cone. In our terms, the area of a frustum of a cone with upper radius r, lower radius R, and side of slant height h is πh(R + r). Archimedes, working in the Euclidean tradition, did not use formulas like this. Rather, he said that the frustum is equal to a disk whose radius is the mean proportional between the slant height and the sum of the two radii—that is, a disk whose radius is . In our exposition, we shall use this fact in the following form: A rectangle whose length is R + r and whose width is h equals the square on the radius of a circle equal to the lateral surface of the frustum. A conical frustum is shown in Fig. 14.1, and the simple way of getting its area is illustrated in Fig. 14.2. To save tedium, we will not repeat Archimedes' proof of this fact, but rather explain it in terms of modern geometry, using formulas.

Figure 14.1 Left: Frustum of a cone of slant height h and upper radius r. Right: Same frustum, turned upside down to exhibit the lower radius R.

Figure 14.2 The frustum cut open. The angle α is to a complete rotation as the radius of the circular section at each point is to the slant distance to the apex of the cone. For the top and bottom circles of the frustum, those slant distances are shown here as r' and R'. Thus R : R' : : r : r' : : α : complete rotation, where r and R are the radii of the upper and lower base of the frustum.

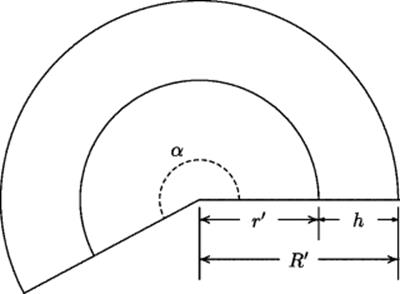
When the frustum shown in Fig. 14.1 is cut open and laid flat, it occupies part of the annulus between two concentric circles of radii r' and R', respectively. The portion α of this annulus occupied by the frustum is directly proportional to the portion of a complete circle the two boundaries of the frustum occupy. That portion is the same for both circles. The full circles would have circumference 2πr' and 2πR', respectively, whereas the portions of them corresponding to the boundaries of the frustum have length 2πr and 2πR, respectively, where r and R are the radii of the boundary circles before the frustum was cut open. In other words, α = r/r' = R/R'. Now the area of the full annulus, as we know, is π(R' ² − r' ²) = π(R' − r')(R' + r') = πh(R' + r'). Hence the portion of it occupied by the cut-open frustum is πh(αR' + αr') = πh(R + r). In other words, the radius of a circle whose area equals the lateral area of the frustum is , as asserted. Notice that the formula works even when the “frustum” is a complete cone, that is, when r = 0. The area of a cone of base radius R and slant height h is πRh. (In the even more extreme case when the cone is flattened into a disk, we get h = R, and this same formula gives the area of the disk.)

This result can be applied to the figures generated by revolving a circle about a diameter with a regular 4n-sided polygon inscribed in it. Archimedes illustrated his argument with n = 4, but we shall illustrate it n = 2, that is, an inscribed octagon. The general idea is sufficiently clear from that case. Because all the right triangles in Fig. 14.3 are similar, we have A' B : AB : : BE : AE : : B' E : EF : : CG : FG : : C' G : GH : : DI : HI : : D' I : IA'. Since these ratios are all equal, we can add the first and second terms of any subset of them without changing the ratio. In particular, then

Since this last term is just AA' (the diameter of the sphere), we get

Since all the chords in this figure are equal to AB, which is the slant height of the cones or frusta generated when the figure is revolved about the diameter AA', each of the rectangles whose sides are AB and BE, AB and B' E + CG, AB and C' G + DI, and AB and D' I is equal to the square whose side is the radius of a circle equal to corresponding cone or frustum. (The sums BE + 0, B' E + CG, C' G + DI, and D' I + 0 are the sums of the two radii of the frusta.)

Figure 14.3 Finding the surface area of a sphere.

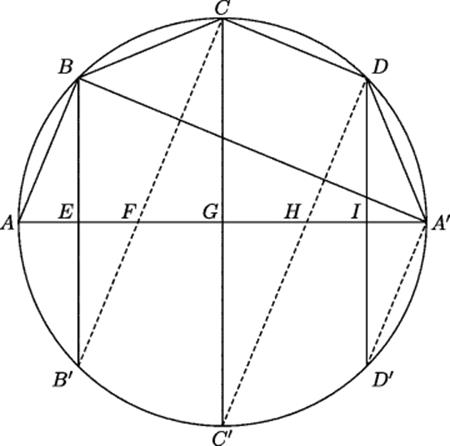
At this point, we need a small fact that is easy to prove metrically, but more complicated to state in Euclid's language: If S₁ and S₂ are squares whose sides are the radii of disks D₁ and D₂ respectively, and S₃ is a square such thatS₃ = S₁ + S₂, then the side of square S₃ is the radius of a disk D₃ such that D₃ = D₁ + D₂. This result is easily proved from the proportionality of disks and the squares on their radii (Proposition 2 of Book 12 of the Elements). When combined with the Pythagorean theorem, this result implies that the disk whose radius is the hypotenuse of a right triangle is the sum of the disks whose radii are the legs.

Thus, the fact (Elements, Book 6, Proposition 16) that when four lines are in proportion, the rectangle on the means equals the rectangle on the extremes means that the rectangle on AB and the sum BE + (B' E + CG) + (C' G + DI) + D' I equals the rectangle on A' B and AA'. But the former, as just noted, is equal to the square on the radius of a disk equal to the sum of all these frusta. This is Proposition 22 of Archimedes' paper: The rectangle on AA' and AB is the square on the radius of a circle equal to the sum of the (cones and) frusta generated by revolving the figure.

The final step is to appeal to the method of exhaustion. If the side AB is chosen sufficiently small, A' B can be made as close as we like to the diameter AA', and the sum of the areas of the frusta can be made as close as we like to the surface of the sphere. Thus, as we would now put it, “in the limit” as the number of sides increases without bound, we find that the radius of a disk equal to the surface of the sphere is AA', the diameter of the sphere. (Proposition 33): The surface of any sphere is equal to four times the greatest circle in it.

This achievement towers above anything found in any of Archimedes' predecessors. In order to get it, he had to make certain definitions about the area of a sphere, definitions that are in full agreement with intuition, but cannot be dispensed with even now. Once those definitions were made, he proved the result with full Euclidean rigor, leaving out no details. This argument is the only ancient expression for a plane region equal to the surface of a sphere that meets Euclidean standards of rigor.

Three remarks should be made on this proof. First, in view of the failure of efforts to square the circle, it seems that the later Greek mathematicians had two “standard” plane regions that could be used for comparing curved surfaces: the circle and the square. Archimedes expressed the surface of a sphere by finding a disk equal to it. Second, Archimedes could certainly have produced the “metric” version of this proof that is usually stated nowadays—namely that the area of a sphere of radius r is 4πr²—since in his work on the measurement of a circle, he showed that a disk equals a right triangle whose legs are the radius and circumference of the disk, and also gave a numerical approximation to the ratio of the circumference and the diameter, which we express by the inequalities .³ Finally, Archimedes did not discover this theorem by Euclidean methods. He told how he came to discover it in his Method.

14.3 The Archimedes Palimpsest

Early in the twentieth century the historian of mathematics J. L. Heiberg, reading in a bibliographical journal of 1899 the account of the discovery of a tenth-century manuscript with mathematical content, deduced from a few quotations that the manuscript was a copy of a work of Archimedes. In 1906 and 1908 he journeyed to Constantinople and established the text, as far as was possible. Attempts had been made to wash off the mathematical text during the Middle Ages so that the parchment could be used to write a book of prayers. The 177 pages of this manuscript contain parts of some of the works just discussed—it is the only source for the work on floating bodies—and a work called Method. The existence of such a work had been known because of the writings of commentators on Archimedes.

14.3.1 The Method

There are quotations from the Method in the Metrica, of Heron of Alexandria, a work that was discovered in 1903. The Method had been sent to the astronomer Eratosthenes as a follow-up to a previous letter that had contained the statements of two theorems without proofs and a challenge to discover the proofs. Both of the theorems involve the volume and surface of solids of revolution. In contrast to his other work on this subject, however, Archimedes here makes free use of the principle now commonly known as Cavalieri's principle, which asserts that if the horizontal sections of two solids are in the same ratio at every elevation, then the volumes of those solids are in that same ratio. Archimedes' Method is a refinement of this principle, obtained by imagining the sections of a region balanced about a fulcrum. The reasoning is that if each pair of corresponding sections balance at distances a and b, then the bodies themselves will balance at these distances, and therefore, by Archimedes' principle of the lever, the area or volume of the two bodies must be have the ratio b : a. Archimedes used this method to prove the following result:

A sphere is four times the cone with base equal to a great circle of the sphere and height equal to its radius. The cylinder with base equal to a great circle of the sphere and height equal to the diameter is half again as large as the sphere.

Archimedes' proof is based on Fig. 14.4. If this figure is revolved about the line CAH, the circle with center at K generates a sphere, the triangle AEF generates a cone, the rectangle LGFE generates a cylinder, and each horizontal line such as MN generates a disk. The point A is the midpoint of CH. Archimedes shows that the area of the disk generated by revolving QR plus the area of the disk generated by revolving OP has the same ratio to the area of the disk generated by revolving MN that AS has to AH. It follows from his work on the equilibrium of planes that if the first two of these disks are hung at H,⁴ they will balance the third disk about A as a fulcrum. Archimedes concluded that the sphere and cone together placed with their centers of gravity at H would balance (about the point A) the cylinder, whose center of gravity is at K.

Figure 14.4 Volumes of sphere, cone, and cylinder.

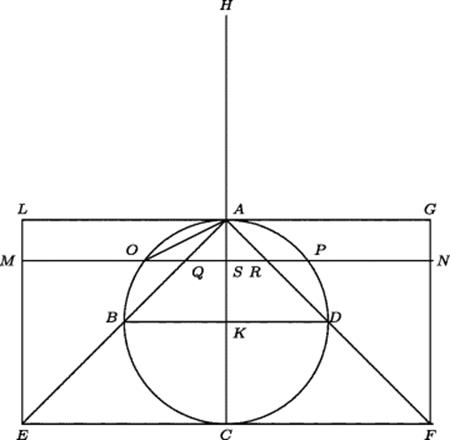
Therefore,

But HA = 2AK. Therefore, the cylinder equals twice the sum of the sphere and the cone AEF. And since it is known that the cylinder is three times the cone AEF, it follows that the cone AEF is twice the sphere. But since EF = 2BD, cone AEF is eight times cone ABD, and the sphere is four times the cone ABD.

From this fact, Archimedes easily deduces the famous result allegedly depicted on his tombstone: The cylinder circumscribed about a sphere equals the volume of the sphere plus the volume of a right circular cone inscribed in the cylinder.

Having concluded the demonstration, Archimedes reveals that this method enabled him to find a planar region equal to the surface of a sphere. He writes

For I realized that just as every circle equals a triangle having as its base the circumference of the circle and altitude equal to the [distance] from the center to the circle [that is, the radius], in the same way every sphere is equal to a cone having as its base the surface of the sphere and altitude equal to the [distance] from the center to the sphere.

Thus, we now imagine two cones: One has a base circle equal to the surface of the sphere and height equal to the radius of the sphere, while the second is circumscribed about the sphere and hence has base circle equal to the equatorial circle of the sphere and height equal to twice its radius. Archimedes had established intuitively that the volume of the sphere was one-third of the former and two-thirds of the latter and, therefore, four-thirds of the cylinder obtained by taking the bottom half of the latter. But this last cylinder has the same height as the first, and therefore the volumes of the two are proportional to their bases. That means the base of the first cylinder (the area of the sphere) is four times the base of the last, which is the area of the equatorial circle. This is how Archimedes came to discover the result, which he then proved by the method of exhaustion (with a few reasonable assumptions about the approximation of areas). The method of exhaustion is very satisfying in settling an argument, but useless as a way of discovering the result. The Method shows us Archimedes' route to that discovery.

14.4 Quadrature of the Parabola

Archimedes used this method of imaginatively “balancing line segments” to show that the area of a parabolic segment is one-third larger than the largest triangle that can be inscribed in it. Having done that, he then proceeded to provide a rigorous proof of this fact using the method of exhaustion.

14.4.1 The Mechanical Quadrature

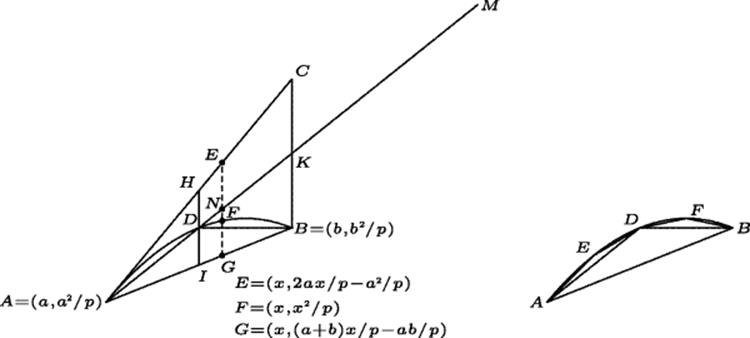
The mechanical proof is illustrated on the left side of Fig. 14.5, where K is the midpoint of the side BC of the triangle ABC and AC is the tangent to the parabola at A. Archimedes showed that the line EG whose midpoint is at N will be exactly balanced about a fulcrum at K if the portion FG of the line is suspended at point M, where AK = KM. He then concluded that the whole triangle ABC in the position where it is would be exactly balanced by the parabolic segment hung at M. Since the center of gravity of the triangle lies one-third of the way from K to A, it follows that ABC is three times the parabolic segment (which, for convenience, we shall refer to as S). But it is easily seen that ABC is four times ABD, and hence S is one-third larger than ABD.

Figure 14.5 Left: Mechanical quadrature of a segment of the parabola py = x². Right: Rigorous quadrature based on the fact that ABD is eight times as large as each of AED and BDF.

14.4.2 The Rigorous Quadrature

Although Archimedes willingly revealed the intuitive considerations that enabled him to solve the difficult problem of quadrature of a parabolic segment, he knew that this argument went beyond the pure methodology of the Euclidean tradition. He therefore followed this mechanical quadrature with a strictly rigorous proof, which we shall now describe.

Archimedes showed using properties of the parabola which we will not take the time to discuss, that if two more triangles AED and BFD are inscribed in the two sections cut off by sides AD and BD of the original triangle (see the right-hand side of Fig. 14.5, then these two triangles together equal exactly one-fourth of triangle ABD. Since adjoining the two new triangles removes more than half of the region between the segment and the triangle, it is clear that repeating this operation will eventually get a finite set of triangles which are together smaller than the parabolic segment, but differ from it by less than any specified magnitude.

Continuing in that way, doubling the number of new triangles at each step while reducing their total area by a factor of 4, he got what we would call an infinite (geometric) series for the magnitude of the parabolic segment:

Since it would not have been acceptable in a proof to speak of the sum of infinitely many terms, Archimedes merely said that it was clear that the sum of the triangles at any stage of the operation was obviously not greater than S. That is, S could not be less than, for example,

But, on the other hand, given any region U smaller than S, one could take enough triangles to get a sum of this form larger than U.

Archimedes observed that multiplying the last term by 4/3 at any stage of the operation would cause the sum of the terms up to that stage to equal 4/3. That is, this finite sum would collapse (“telescope,” we might say), if the last term were multiplied by , since

This relation causes the last two terms here to “merge” into . But then the last two terms of the altered sum merge similarly into , and this argument can be repeated until the whole sum reduces to . Thus, he had shown that

Hence the sum on the left is always less than , but given any region U smaller than , one could take enough triangles to get a sum of this form larger than U.

It is now clear that S must equal . If S were larger than , the first argument shows that we could take enough triangles to get a sum that is larger than , which contradicts the second argument. Exactly the same reasoning applies if we assume is larger than S.

Observe that Archimedes has given a proof that is entirely finitistic and has not mentioned any infinite series here. He has proved two things: first, if U > S, then ; second, if U < S, then . The assumption would (by the second result) imply that , which is absurd, and since the first result similarly rules out the possibility that , the only remaining possibility is that . In so doing, he has given exactly the kind of epsilon–delta proof that calculus students so often find mystifying. Newton once defended his formal rules in calculus (which we now establish rigorously by using the notion of a limit) by saying that it would be possible to justify them using the trichotomy of the ancient mathematicians but that there was no need to undergo such tedium. He must have had this method of exhaustion in mind.

Problems and Questions

Mathematical Problems

14.1 Use analytic geometry to justify the balancing in Archimedes' mechanical quadrature of the parabola. [Hint: Show that EG : FG : : (b − a) : (b − x). Use the expressions shown for the points E, F, and G. Here the parabola is assumed to have the equation py = x², where p is negative, since the parabola opens downward, and we take the zero value of y to be the highest point on the parabola.]

14.2 Prove that a disk D that equals the sum of disks D₁ of radius r₁ and D₂ of radius r₂ necessarily has radius r satisfying . This is easy to do using the formula A = πr². Try to do it using only the fact that if P₁ and P₂are similar polygons with a pair of corresponding sides equal to r₁ and r₂, respectively, then P₁ : P₂ : : D₁ : D₂. (Use the result of Proposition 31 of Book 6 of the Elements, which asserts that the Pythagorean theorem holds for any similar polygons attached to the sides of a right triangle.)

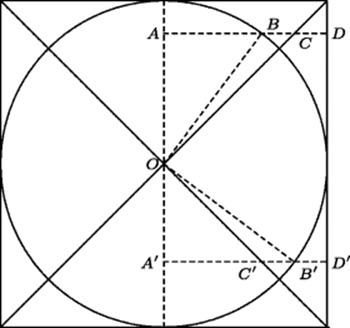
14.3 Give an alternative proof of Archimedes' result on the sphere and cylinder by showing (see Fig. 14.6) that . Hence the sum of the sections of the cone and sphere equals the section of the cylinder.

Figure 14.6 When the square circumscribed about the circle is revolved about its vertical midline (the line through A and A'), it generates the cylinder circumscribed about the sphere generated by the circle. The diagonals of the square generate a double-napped cone inscribed in the cylinder. The cylindrical section equals the sum of the sections of the cone and sphere.

Historical Questions

14.4 What advances in geometry, beyond the basic results found in the Elements, are due to Archimedes?

14.5 What achievements of Archimedes show his versatility as a mathematician and scientist?

14.6 How did Archimedes discover that a sphere equals a cone whose base is the surface area of the sphere and whose height is the radius of the sphere?

Questions for Reflection

14.7 Archimedes has a reputation as the greatest mathematician of antiquity and one of the three greatest of all time. What criteria can you imagine being applied to justify this judgment?

14.8 Why, in your opinion, did Archimedes choose to give both a mechanical and a strict Euclidean proof of his quadrature results?

14.9 It was mentioned above that some scholars now think Euclid was a contemporary of Archimedes rather than a predecessor. If that is so, how do you account for the fact that the Elements does not contain any material from Archimedes' treatises and that some of Archimedes works seem to refer to the Elements?

Notes

1. This claim was made by Professor Salvatore Ciancio (1965) on the basis of several criteria, including the location and date of the relics and a gold signet ring found in the crematory urn inside the tomb and bearing the ancient seal of the city of Alexandria. The sphere and cylinder mentioned by Cicero were not part of the find. The claim was contradicted at the time by the Curator of Antiquities in Syracuse Prof. Bernabò Brea. Another counterclaim is made by D. L. Simms in “The trail for Archimedes' tomb,” Journal of the Warburg and Courtauld Institute, 53 (1990), pp. 281–286 (reference taken from the Worldwide Web). More information can be obtained at the address http://www.mcs.drexel.edu/~crorres/Archimedes/contents.html.

2. That is, a book in which earlier work has been written and washed off so that new material could be entered in it.

3. These two results, interpreted in our language, imply that one-dimensional π—the ratio of circumference to diameter—and two-dimensional π—the ratio of a disk to the square on its radius—are the same number. But, being irrational, it was not a number to Archimedes.

4. In looking at Fig. 14.4, you have to imagine that gravity is acting horizontally rather than vertically.