Hellenistic and Roman Geometry - Greek Mathematics From 500 BCE to 500 CE - A brief course

The history of mathematics: A brief course (2013)

Part III. Greek Mathematics From 500 BCE to 500 CE

Chapter 16. Hellenistic and Roman Geometry

No sensible person would attempt to study modern geometry using Euclidean methods. The difficulty with such an approach is not only that the kind of proof required is a very long and tedious way of proving even the simplest results. The basic objects underlying almost all of the geometry of Euclid, Archimedes, and Apollonius were few and simple, being formed from straight lines, planes, circles, and combinations of them. The conic sections are already near the limit of tolerable complexity that can be generated from these tools. The small number of more complicated curves considered in ancient times, such as the spiral of Archimedes, the quadratrix of Hippias, and the conchoid of Nicomedes were created by introducing the concept of motion into the basically static geometry of Euclid's Elements. They were pictured as the path of a point moving under simple conditions that combined straight-line and circular motion. Curved three-dimensional figures such as spheres and cones were likewise pictured as the result of translating or revolving lines or circles. In contrast, the kinds of curves studied in modern mathematics, such as the graphs of polynomials of degree three and higher or transcendental functions such as the logarithm or the sine, are impossible to analyze using these tools. The Euclidean methodology set limits to the growth of geometry, and those limits were nearly reached by the end of the third century BCE. Still, a few later mathematicians attempted to go beyond beyond the achievements of Archimedes and Apollonius, and they produced some good work over the next few centuries.

16.1 Zenodorus

The astronomer Zenodorus lived in Athens in the century following Apollonius. Although his exact dates are not known, he is mentioned by the late third-century mathematician Diocles in his book On Burning Mirrors¹ and by Theon of Alexandria in his commentary on Ptolemy's Almagest. According to Theon, Zenodorus wrote On Isoperimetric Figures, in which he proved four theorems: (1) If two regular polygons have the same perimeter, the one with the larger number of sides encloses the larger area; (2) a circle encloses a larger area than any regular polygon whose perimeter equals its circumference; (3) of all polygons with a given number of sides and perimeter, the regular polygon is the largest; (4) of all closed surfaces with a given area, the sphere encloses the largest volume. With the machinery

inherited from Euclidean geometry, Zenodorus could not have hoped for any result more general than these. Let us examine his proof of the first two, as reported by Theon.

In Fig. 16.1, let ABΓ and ΔEZ be two regular polygons having the same perimeter, with ABΓ having more sides than ΔEZ. Let H and Θ be the centers of these polygons, and draw the lines from the centers to two adjacent vertices and their midpoints, getting triangles BΓH and EZΘ and the perpendicular bisectors of their bases HK and ΘΛ. Then, since the two polygons have the same perimeter but ABΓ has more sides, BK is shorter than EΛ. Mark off M on EΛ so that MΛ = BK. Then if P is the common perimeter, we have EΛ : P : : ∠ EΘΛ : 4 right angles and P : BK : : 4 right angles : ∠ BHK. By composition then (see Subsection 12.2.3 of Chapter 12), EΛ : BK : : ∠ EΘΛ : ∠ BHK, and therefore EΛ : MΛ : : ∠ EΘΛ : ∠ BHK. But, Zenodorus claimed, the ratio EΛ : MΛ is larger than the ratio ∠EΘΛ : ∠ MΘΛ, asking to postpone the proof until later. Granting that lemma, he said, the ratio ∠EΘΛ : ∠ BHK is larger than the ratio ∠EΘΛ : ∠ MΘΛ, and therefore ∠BHK is smaller than ∠MΘΛ. It then follows that the complementary angles ∠HBK and ∠ΘMΛ satisfy the reverse inequality. Hence, copying ∠HBK at M so that one side is along MΛ, we find that the other side intersects the extension of ΛΘ at a point N beyond Θ. Then, since triangles BHK and MNΛ are congruent by angle–side–angle, it follows that HK = NΛ > ΘΛ. But the areas of the two polygons are and , and therefore ABΓ is the larger of the two.

Figure 16.1 Two theorems of Zenodorus. Top: When two regular polygons have the same perimeter, the one with the larger number of sides is larger. Bottom: A circle is larger than a regular polygon whose perimeter equals the circumference of the circle.

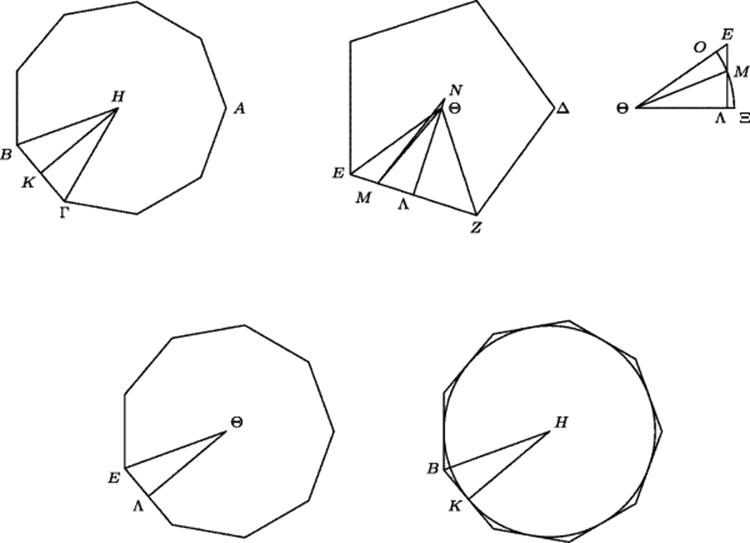
The proof that the ratio EΛ : MΛ is larger than the ratio ∠EΘΛ : ∠ MΘΛ was given by Euclid in his Optics, Proposition 8. But Theon does not cite Euclid in his quotation of Zenodorus. He gives the proof himself, implying that Zenodorus did likewise. The proof is shown on the top right in Fig. 16.1, where the circular arc ΞMO has been drawn through M with Θ as center. Since the ratio EΘM : sector OΘM is larger than the ratio MΘΛ : sector MΘΞ (the first triangle is larger than its sector, the second is smaller), it follows, interchanging means, that EΘM : MΘΛ > sector OΘM : sector MΘΞ. But EΘM : MΘΛ : : EM : MΛ, since the two triangles have the same altitude ΘΛ measured from the base line EMΛ. And sector OΘM : sector MΘΞ : :∠ EΘM : ∠ MΘΛ. Therefore, EM : MΛ is larger than the ratio ∠EΘM : ∠ MΘΛ, and it then follows that EΛ : MΛ is larger than ∠EΘΛ : ∠ MΘΛ. (See the explanation of the addition of ratios in Subsection 12.2.3 of Chapter 12.)

Zenodorus' proof that a circle is larger than a regular polygon whose perimeter equals the circumference of the circle is shown at the bottom of Fig. 16.1. Given such a polygon and circle, circumscribe a similar polygon around the circle. Since this polygon is “convex on the outside,” as Archimedes said in his treatise on the sphere and cylinder, it can be assumed longer than the circumference. (Both Archimedes and Zenodorus recognized that this was an assumption that they could not prove; Zenodorus cited Archimedes as having assumed this result.) That means the circumscribed polygon is larger than the original polygon since it has a larger perimeter. But then by similarity, HKis larger than ΘΛ. Since a circle equals half of the rectangle whose sides are its circumference and radius (proved by Archimedes), while a regular polygon is half of the rectangle whose sides are its perimeter and its apothem,² it follows that the circle is larger.

16.2 The Parallel Postulate

We saw in Chapter 12 that there was a debate about the theory of parallel lines in Plato's Academy, as we infer from the writing of Aristotle. This debate was not ended by Euclid's decision to include a parallel postulate explicitly in the Elements. This foundational issue was discussed at length by the Stoic philosopher Geminus, whose dates are a subject of disagreement among experts, but who probably lived sometime between 50 BCE and 50 CE. Geminus wrote an encyclopedic work on mathematics, which has been entirely lost, except for certain passages quoted by Proclus, Eutocius, and others. Proclus said that the parallel postulate should be completely written out of the list of postulates, since it is really a theorem. The asymptotes of hyperbolas provided the model on which he reasoned that converging is not the same thing as intersecting. But still he thought that such behavior was impossible for straight lines. He claimed that a line that intersected one of two parallel lines must intersect the other,³ and he reports a proof of Geminus that assumes in many places that certain lines drawn will intersect, not realizing that by doing so he was already assuming the parallel postulate.

Proclus also reports an attempt by Ptolemy to prove the postulate by arguing that a pair of lines could not be parallel on one side of a transversal “rather than” on the other side. (Proclus did not approve of this argument.) But the assumption that parallel lines are symmetric under reflection through a common transversal that is perpendicular to one of them is a Euclidean theorem that does not extend to non-Euclidean geometry. These early attempts to prove the parallel postulate began the process of unearthing more and more plausible alternatives to the postulate, but of course did not lead to a proof of it.

16.3 Heron

We have already noted some of the restrictions that Euclid imposed on plane geometry, one of them being that lines are not associated with numbers. After Apollonius, however, the metric aspects of geometry began to resurface in the work of later writers. One of these writers was Heron (ca. 10–ca. 75), who wrote on mechanics. He probably lived in Alexandria. Pappus discusses his work in Book 8 of his Collection. Heron's geometry is much more concerned with measurement than was the geometry of Euclid. The change of interest in the direction of measurement and numerical procedures signaled by his Metrica is shown vividly by his repeated use (130 times, to be exact) of the word area (embadón), a word never once used by Euclid, Archimedes, or Apollonius.⁴ There is a difference in point of view between saying that two plane figures are equal and saying that they have the same area. The first statement is geometrical and is the stronger of the two. The second is purely numerical and does not necessarily imply the first. Heron discusses ways of finding the areas of triangles from their sides. After giving several examples of triangles that are either integer-sided right triangles or can be decomposed into such triangles by an altitude, such as the triangle with sides of length 13, 14, 15, which is divided into a 5–12–13 triangle and a 9–12–15 triangle by the altitude to the side of length 14, he gives “a direct method by which the area of a triangle can be found without first finding its altitude.” He gave as an example a triangle whose sides were 7, 8, and 9 units. His prescription was: Add 9 and 8 and 7, getting 24. Take half of this, getting 12. Subtract 7 units from this, leaving 5. Then subtract 8 from 12, leaving 4. Finally, subtract 9, leaving 3. Multiply 12 by 5, getting 60. Multiply this by 4, getting 240. Multiply this by 3, getting 720. Take the square root of this, and that will be the area of the triangle. He went on to explain that since 720 is not a square, it will be necessary to approximate, starting from the nearest square number, 729.

This result seems anomalous in Greek geometry, since Heron is talking about multiplying an area by an area. That is probably why he emphasizes that his results are numerical rather than geometric. His proof is based on Fig. 16.2, in which one superfluous line has been omitted to streamline it. In the following proof, some rewording has been done to accommodate this minor modification of the figure. This figure shows an arbitrary triangle ABΓ with its inscribed circle, and the radii of that circle to the points of contact HΔ, HE, and HZ drawn. These three radii are all congruent, and each is perpendicular to the corresponding side. Denote their common length by r. The lines HA, HB, and HΓ from the center of the inscribed circle to the vertex are the bisectors of the angles. We have marked one of each congruent pair at each vertex as α, β, and γ. It is then clear that α + β + γ is half the sum of the angles of the triangle, that is, it is equal to a right angle.

Figure 16.2 Proof of Heron's method of computing the area of a triangle from the lengths of its sides.

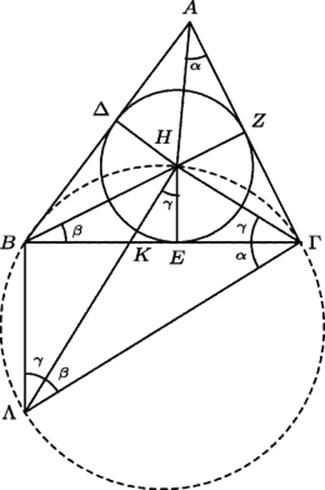
Because of the way the triangle is partitioned into three triangles AΓH, ABH, and BΓH, we can see that its area is , which is easily seen to be , where Σ is half the perimeter of the triangle. There are many ways different ways of expressing Σ as a sum of lines, among them . We shall use all three of these expressions below.

Heron claims that the area is numerically , which, using these three expressions for Σ, we can write as .

To see why this expression represents the area of the triangle, draw lines BΛ and HΛ from B and H perpendicular, respectively, to BΓ and HΓ and intersecting at the point Λ. The quadrilateral ΛBHΓ is cyclic—that is, can be inscribed in a circle. This fact holds because the two right triangles ΛBΓ and ΛHΓ have ΛΓ as a common hypotenuse. Since the hypotenuse of a right triangle is a diameter of the circumscribed circle, that circumscribed circle is the same for both. Then, since ∠HΓB and ∠BΛH are both inscribed in the same arc , it follows that angle BΛH = γ. Similarly, since ∠HΛΓ and ∠HBΓ are both inscribed in the same arc , we have ∠HΛΓ = β. Adding, we find that ∠BΛΓ = β + γ, and therefore the complementary angle BΓΛ equals α. Finally, since both HE and BΛ are perpendicular to BΓ, we have ∠ΛHE = ∠ BΛH = γ. We therefore have two pairs of similar right triangles: ΓBΛ and AZH, and BΛK and EHK.

From these two similar triangles, we obtain the fundamental results that and . By composition, , that is, . Also, since HE is the altitude to the hypotenuse of the right triangle KHΓ, we have . These last two relations are the key to proving the result.

It is now possible to obtain the required expression for the area by plodding through the following sequence of equalities, each of which follows trivially from the one above.

equation

The result is therefore proved.

16.4 Roman Civil Engineering

Dilke (1985, pp. 88–90) describes the use of geometry in Roman civil engineering as follows. The center of a Roman village would be at the intersection of two perpendicular roads, a (usually) north–south road called the kardo maximus (literally, the main hinge) and an east–west road called decumanus maximus, the main tenth. Lots were laid out in blocks (insulæ) called hundredths (centuriæ), each block being assigned a pair of numbers, telling how many units it was dextra decumani (right of the decumanus, that is, north⁵) or sinistra decumani (left of the decumanus, that is, south) and how many units it was ultra kardinem (beyond the kardo, that is, west) or citra kardinem(within the kardo, that is, east).

A collection of Roman writings on surveying was collected, translated into German, and published in Berlin in the middle of the nineteenth century. This two-volume work bears the title Corpus Agrimensorum Romanorum, the word agrimensor (field measurer) being the Latin name for a surveyor, as already noted in Chapter 7. A medieval town laid out in accordance with the scheme just described is shown in that work. Looking at it, one cannot help thinking of a rectangular coordinate system, regarding the kardo and decumanus, with the coordinatization of the centuriæ, as prefigurations of our concept of coordinate axes. The spherical equivalent was used by Ptolemy, as we shall see in the next chapter, and his latitude and longitude did influence the development of analytic geometry.

Among the agrimensores was one named M. Iunius Nipsus, a second-century surveyor, who, according to Dilke (1985, p. 99), gives the following directions for measuring the width of a river (Fig. 16.3).

Figure 16.3 Nipsus' method of computing the width of a river.

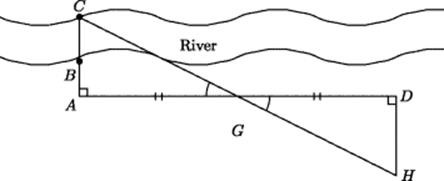
You mark the point C on the opposite bank from B (a part of the procedure Nipsus neglects to mention until later), continue the straight line CB to some convenient point A, lay down the crossroads sign at A, and then move along the direction perpendicular to AC until you reach a point G, where you erect a pole, then continue on to D so that GD = AG. You then move away from D along the direction perpendicular to AD until you see G and C in a straight line from the point H. Since the triangles AGC and DGH are congruent (by angle–side–angle), it follows that CB = CA − AB = HD − AB.

For this procedure to work in practice, it is necessary to have an accessible and level piece of land covering the lines shown as AD and DH. If the river is large, such a stretch of land may not exist, since the river banks are likely to be hilly. In its neglect of similar triangles, this method seems a large step backward in applied geometry.

Problems and Questions

Mathematical Problems

16.1. Find the area of a triangle whose sides are 24 cm, 37 cm, and 43 cm.

16.2. Express the area of a regular n-gon in terms of its perimeter P, using trigonometry. What happens to this area as n tends to infinity?

16.3. Suppose that four squares A, B, C, and D are in proportion, that is, A : B : : C : D. Let their sides be respectively a, b, c, and d. Prove that the sides are also in proportion, that is, a : b : : c : d, using the Eudoxan definition of proportion. [Hint: Let m and n be any two integers. You need to show that if ma > nb, then mc > nd. Assuming ma > nb, prove that m²A > n²B. Why does m²A > n²B imply m²C > n²D, and why does this last inequality imply mc > nd?]

Historical Questions

16.4. What new directions did Greek geometry explore after the treatises of Archimedes and Apollonius?

16.5. What isoperimetric inequalities were stated and proved by Zenodorus?

16.6. What relation did Heron establish between the lengths of the three sides of a triangle and its area?

Questions for Reflection

16.7. Which of the two writers discussed above, Heron and Zenodorus, worked more in the spirit of Euclid's Elements?

16.8. How did Heron regard the ratio of two lines? Did he handle it as Eudoxus recommended?

16.9. Why did the elaborate system of Euclidean geometry apparently play no role in the magnificent engineering feats (roads, aqueducts, and the like) of the Romans?

Notes

1. Arabic manuscripts of this work have revealed that Diocles and Zenodorus actually collaborated (Toomer, 1976).

2. An apothem—not to be confused with an apothegm—is the line from the center of a polygon perpendicular to a side. In this case, the apothem is ΘΛ.

3. This assertion is an assumption equivalent to the parallel postulate and obviously equivalent to the form of the postulate commonly used nowadays, known as Playfair's axiom, after the Scottish geometer John Playfair (1748–1819): Through a given point not on a line, only one parallel can be drawn to the line.

4. Reporting (in his commentary on Ptolemy's Almagest) on Archimedes' Measurement of a Circle, however, Theon of Alexandria did use this word to describe what Archimedes did; but that usage was anachronistic. In his work on the sphere, for example, Archimedes referred to its surface (epipháneia), not its area. On the other hand, Dijksterhuis (1956, pp. 412–413) reports the Arabic mathematician al-Biruni as having said that “Heron's formula” is really due to Archimedes. Considering the contrast in style between the proof and the applications, it does appear plausible that Heron learned the proof from Archimedes. Heath (1921, Vol. 2, p. 322) endorses this assertion unequivocally.

5. This orientation presumes the map user is looking west along the decumanus maximus. Often, the town forum would be located at the intersection of the two main roads.