The history of mathematics: A brief course (2013)
Part IV. India, China, and Japan 500 BCE-1700 CE
In the six chapters that constitute this part, we shall survey a long period of development of mathematics in three cultures that grew up independent of the mathematics that flourished around the Mediterranean Sea. A different “flavor,” more numerically oriented and strongly algebraic, will be seen in all three places. This numerical orientation will be especially noted in geometry, where the approach is not the axiomatic, metric-free Euclidean system. Nonobvious relations among geometric figures are demonstrated using congruence, dissection, and the Pythagorean theorem.
The usual disclaimer applies in this part. It is a very small sample of what could be said; and for more details, the reader should consult the references cited in the corresponding chapters.
Contents of Part IV
1. Chapter 19 (Overview of Mathematics in India) contains a survey of some major achievements and outstanding mathematicians in India (including modern Pakistan) from the earliest times to the twentieth century. By looking at the prefaces to some of the great treatises, we gain some idea of the motivation for creating this knowledge. Again, the names mentioned are only a few of a large number that are worthy of mention.
2. Chapter 20 (From the Vedas to Aryabhata I) discusses the mathematics of the Hindu Vedas beginning around 500 BCE and the work of Aryabhata I (476–550).
3. Chapter 21 (Brahmagupta, the Kuttaka, and Bhaskara II) discusses the work of two more outstanding mathematicians from the seventh through twelfth centuries CE: Brahmagupta (598–670), and Bhaskara II (1114–1184). We end the story at that point, even though mathematics continued to flourish in India with no break at the end of the twelfth century, even anticipating some parts of the calculus.
4. Chapter 22 (Survey of Chinese Mathematics) is devoted to the Chinese development of arithmetic, algebra, and geometry to meet practical administrative needs. The treatises involved include the ancient Zhou Bi Suan Jing(Arithmetical Classic of the Zhou), which probably dates from a time earlier than 200 BCE, and the Han-Dynasty (200 BCE –200 CE) document Jiu Zhang Suanshu (Nine-Chapter Mathematical Treatise), which can be regarded as the fundamental text on classical Chinese mathematics.
5. Chapter 23 (Later Chinese Algebra and Geometry) discusses the study of higher-order equations by Chinese mathematicians and the advanced geometry of Liu Hui (220–280), Zu Chongzhi (420–501), and Zu Geng (ca. 450–ca. 520).
6. Chapter 24 (Traditional Japanese Mathematics) discusses the mathematics of Japan as it was developed from the Chinese classic works and elaborated during the Tokugawa Era from 1600 through 1867. This subject, called wasan (Japanese-style computation), is contemporaneous with a phenomenon that is apparently unique to Japan, namely, the hanging of votive plaques at Shinto and Buddhist shrines with worked-out mathematical problems on them. These plaques are called sangaku (computational framed pictures).
Chapter 18. Pappus and the Later Commentators
The last few centuries of mathematics in the Greek tradition showed clear evidence of decline in geometry. Except for Pappus and a few others, most geometric work done during this period was commentary on earlier work. On the other hand, as we saw in Chapter 9, algebra arose in a form that we can recognize, in the works of Diophantus, although it was more closely connected to number theory than to geometry.
18.1 The Collection of Pappus
Almost nothing is known about the life of Pappus. The tenth-century encyclopedia known as the Suda says the following about him:
Pappus, of Alexandria, philosopher, lived about the time of the Emperor Theodosius the Elder [who ruled from 379 to 395], when Theon [of Alexandria] the Philosopher, who wrote the Canon of Ptolemy, also flourished.
However, a table written by Theon himself mentions the emperor Diocletian, who ruled from 284 to 305, and says of his reign, “Pappus wrote during that time.”
The Suda is an unreliable source. (We shall see below that it says Hypatia was the wife of Isodoros, who was, like Hypatia, a neo-Platonist philosopher, probably one of the last. He could not have been her husband, since he lived nearly a century later.) Thus, we give a higher credibility to Theon. But there is circumstantial evidence that he also got it wrong, since Pappus wrote a commentary on Ptolemy's Almagest and in it revealed that he had observed an eclipse of the sun on October 18, 320. He is therefore somewhat later than Theon thought and earlier than the author of the Suda thought. His most probable dates are from around 290 to 350, and his main work, the Collection(Συναγωγ´η = Synag![]() g
g![]() ) was written in the early-to-mid fourth century.
) was written in the early-to-mid fourth century.
Heath describes this work as follows:
Obviously written with the object of reviving the classical Greek geometry, it covers practically the whole field. It is, however, a handbook or guide to Greek geometry rather than an encyclopædia; it was intended, that is, to be read with the original works (where still extant) rather than to enable them to be dispensed with.
In fact, it was too late to revive classical Greek geometry. Its potential had already been exhausted long before, and the only way for geometry to make further progress was to adopt new methods. Those methods were not to show up in the West until the time of Fermat, Pascal, and Descartes, some 1300 years later. With that as preface, let us look into the Collection.
18.1.1 Generalization of the Pythagorean Theorem
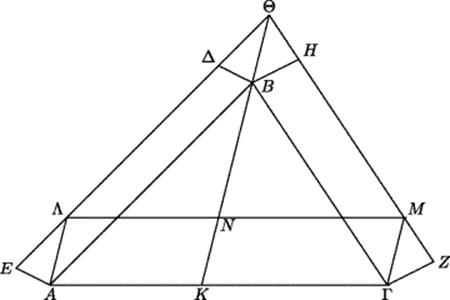
Book 4 of the Collection contains a famous generalization of the Pythagorean theorem: Given any triangle ABΓ and any parallelograms BΓZH and ABΔE constructed on two sides, it is possible to construct (with straightedge and compass) a parallelogram AΓMΛ on the third side equal in area to the sum of the other two (see Fig. 18.1).
Figure 18.1 Pappus' generalization of the Pythagorean theorem.
18.1.2 The Isoperimetric Problem
In Book 5 Pappus states almost verbatim the argument that Theon of Alexandria, quoting Zenodorus, gave for the proof of the isoperimetric inequality. Pappus embroiders the theorem with a beautiful literary device, however. He speaks poetically of the divine mission of the bees to bring from heaven the wonderful nectar known as honey and says that in keeping with this mission they must make their honeycombs without any cracks through which honey could be lost. Being endowed with a divine sense of symmetry as well, the bees had to choose among the regular shapes that could fulfill this condition—that is, triangles, squares, and hexagons. They chose the hexagon because a hexagonal prism required the least material to enclose a given volume, out of all the possible prisms whose base would tile the plane.1
18.1.3 Analysis, Locus Problems, and Pappus' Theorem
Book 7 of the Collection is a treasure trove of fascinating information about Greek geometry for several reasons. First, Pappus describes the kinds of techniques used to carry on the research that was current at the time. He lists a number of books of this analysis and tells who wrote them and what their contents were, in general terms, thereby providing valuable historical information. What he means by analysis, as opposed to synthesis, is a kind of algebraic reasoning in geometry. As he puts it, when a construction is to be made or a relation is to be proved, one imagines the problem to have been solved and then deduces consequences connecting the result with known principles, after which the process is reversed and a proof can be synthesized. This process amounts to thinking about objects determined implicitly in terms of properties that they must have, but not explicitly identified; when applied to numbers—that is, starting with properties that a number must have and deducing its explicit value from those properties—that process is algebra.
A second point of interest in Book 7 is a discussion of locus problems, such as those in Apollonius' Conics. This discussion exerted a strong influence on the development of geometry in seventeenth-century France, as we noted in Chapter 15 and will discuss further in Chapter 32. Several propositions from Euclid's Data, which was discussed in Section 13.2 of Chapter 13, inspired Pappus to create a very general proposition about plane loci. Referring to the points of intersection of a set of lines, he writes:
To subsume all these discoveries in a single proposition, we have written the following. If three points are fixed on one line. . .and all the others except one are confined to given lines, then that last one is also confined to a given line. This is asserted only for four lines, no more than two of which intersect in the same point. It is not known whether this assertion holds for every collection of lines.
This theorem is illustrated in Fig. 18.2, using analytic geometry. To discover this theorem without invoking the power of algebra was an impressive feat. Pappus could not have known that he had provided the essential principle by which a famous theorem of projective geometry known as Desargues' theorem was to be proved 1400 years later. (See Chapter 31.) Desargues knew the work of Pappus, but may not have made the connection with this theorem. The connection was pointed out by van der Waerden (1963, p. 287), who suggests how the theorem may have been proved originally, without analytic geometry.
Pappus discusses the three-and four-line locus for which the mathematical machinery is found in Book 3 of Apollonius' Conics. For these cases the locus is always one of the three conic sections. Pappus mentions that the two-line locus is a planar problem; that is, the solution is a line or circle. He says that a point satisfying the conditions of the locus to five or six lines is confined to a definite curve (a curve “given in position” as the Greeks said), but that this curve is “not yet familiar and is merely called a curve.” The curve is defined by the condition that the rectangular parallelepiped spanned by the lines drawn from a point to three fixed lines bears a fixed ratio to the corresponding parallelepiped spanned by the lines drawn to three other fixed lines. In our terms, this locus is a cubic curve.
Still a third point of interest is connected with the extension of these locus problems. Pappus considers the locus to more than six lines and says that a point satisfying the corresponding conditions is confined to a definite curve. This step was important, since it proposed the possibility that a curve could be determined by certain conditions without being explicitly constructible. Moreover, it forced Pappus to go beyond the usual geometric interpretation of products of lines as rectangles. Noting that “nothing is subtended by more than three dimensions,” he continues:
It is true that some of our recent predecessors have agreed among themselves to interpret such things, but they have not made a meaningful clear definition in saying that what is subtended by certain things is multiplied by the square on one line or the rectangle on others. But these things can be stated and proved using composite ratios.
It appears that Pappus was on the very threshold of the creation of the modern concept of a real number as a ratio of lines. Why did he not cross that threshold? One reason may have been that he was held back by the cumbersome Euclidean definition of a composite ratio, discussed in Section 12.2 of Chapter 12. But there was a further reason: He wasn't interested in foundational questions. He made no attempt to prove or justify the parallel postulate, for example. And that brings us to the fourth attraction of Book 7. In that book Pappus investigated some very interesting problems, which he preferred to foundational questions. After concluding his discussion of the locus problems, he implies that he is merely reporting what other people, who are interested in them, have claimed. “But,” he says,
after proving results that are much stronger and promise many applications,. . .to show that I do not come boasting and empty-handed. . .I offer my readers the following: The ratio of rotated bodies is the composite of the ratio of the areas rotated and the ratio of straight lines drawn similarly [at the same angle] from their centers of gravity to the axes of rotation. And the ratio of incompletely rotated bodies is the composite of the ratio of the areas rotated and the ratio of the arcs described by their centers of gravity.
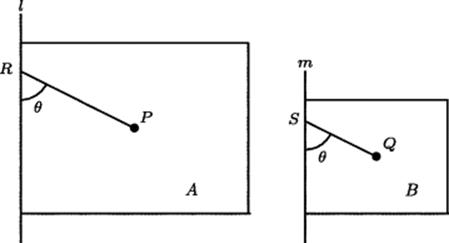
The statement of these theorems shows that Pappus is working in the metric-free tradition of Euclid. He does not use the word volume at any point, much less say what the volume of any particular solid of revolution is. Instead, he refers only to the ratios of such solids, just as Euclid would have done. To elaborate on this language, if a plane figure A having point P as center of gravity is rotated about a line l, generating a solid X, and a plane figure B having point Q as center of gravity is rotated about a line m, generating a solid Y, and if line segments PR and QS are drawn from P and Q respectively to points R on l and S on m, making the same angle at R and S, then X : Y : : A : B . PR : QS. The simple case when A and B are rectangles and the axes of rotation l and m are edges of A and B respectively is shown in Fig. 18.3.
From Propositions 32 and 34 of Book 11 of the Elements, it was known that parallelepipeds having equal bases are proportional to their altitudes and parallelipeds having equal altitudes are proportional to their bases. It is not difficult then to show that the ratio of two parallelepipeds is the composite of the ratios of their bases and altitudes. To do so, let U and V be parallelepipeds having bases A and B, respectively, and altitudes h and k. We wish to show that U : V : : A : B . h : k. In accordance with Euclid's definition of the composite ratio, we need three quantities a, b, and c, all of the same kind, such that A : B : : a : b and h : k : : b : c. By definition A : B.h : k is a : c.
We thus need to show that U : V : : a : c in the notation just introduced. To do so, suppose m and n are any two positive integers such that ma > nc. By Archimedes' principle,2 there is some positive integer r such that r(ma − nc) > b, and hence some integer s such that rma > sb > rnc. Since A : B : : a : b, it follows that rmA > sB; and similarly (because h : k : : b : c) we have sh > rnk. Therefore the parallelepiped having base rmA and altitude sh is larger than the parallelepiped having base sB and altitude rnk. However, since parallelepipeds having the same base are proportional to their altitudes and vice versa, the former of these is exactly rms times as large as P and the latter is rnstimes as large as Q. Canceling rs in this statement, we conclude that mP is larger than nQ, which is precisely what the Eudoxan definition of proportion demands. (Of course, the same argument needs to be repeated with the inequality reversed and then repeated again with the inequality replaced by equality in order to satisfy all three of the conditions of the Eudoxan definition of proportion, but that is an easy exercise for the reader.)
Pappus' theorem is easy to prove for rectangles revolved about one of their sides. If the rectangle has sides a and b and is revolved about the side of length a, it generates a cylinder whose base has radius b and whose altitude is a. It is well known that such a cylinder is proportional to a parallelepiped with square base of side b and altitude a. Now the distance r from the axis to the center of gravity in this case is ![]() , so that the cylinder is also proportional to a rectangular parallelepiped having a base of sides b and r and altitude a. However, that parallelepiped can also be regarded as having a rectangular base of sides a and b and altitude r. Since we have shown above that parallelepipeds are proportional to the composite ratio of their bases and altitudes, it follows that this cylinder is proportional to the composite of the rectangle of sides a and b and the line r, as asserted. Thus, if we have two such rectangles R1 and R2 with sides a1, b1 = 2r1 and a2, b2 = 2r2, generating cylinders C1 and C2, we can say that C1 : C2 : : R1 : R2 . r1 : r2. It is then not difficult to get the same theorem for two rectangles, one of which is rotated about any line parallel to one of its sides. You simply “fill in” the space between the rectangle and the axis of rotation with another rectangle so as to make a larger rectangle of the same height. If the original rectangle is a × b and the filled-in portion is a × c, then the two together will be a × (b + c). The centroid of the original will be at distance c + b/2 from the axis, while the centroid of the one touching the axis of rotation will be at distance c/2 from that axis. The centroid of the two together will be at distance (b + c)/2 from the axis. Applying the original theorem to the two together, we find that the large cylinder is proportional to a parallelepiped with base a × (b + c) and altitude (b + c)/2, while the cylinder generated by the portion of the rectangle touching the axis of rotation is proportional to a parallelepiped with base that is a × c and altitude c/2. Hence the cylindrical annulus generated by the original rectangle, which is a parallelepiped that has base a × b and altitude c + b/2, is proportional to the difference of these two. The rest of the proof is now easy and is left as an exercise, which the reader may do in modern notation.
, so that the cylinder is also proportional to a rectangular parallelepiped having a base of sides b and r and altitude a. However, that parallelepiped can also be regarded as having a rectangular base of sides a and b and altitude r. Since we have shown above that parallelepipeds are proportional to the composite ratio of their bases and altitudes, it follows that this cylinder is proportional to the composite of the rectangle of sides a and b and the line r, as asserted. Thus, if we have two such rectangles R1 and R2 with sides a1, b1 = 2r1 and a2, b2 = 2r2, generating cylinders C1 and C2, we can say that C1 : C2 : : R1 : R2 . r1 : r2. It is then not difficult to get the same theorem for two rectangles, one of which is rotated about any line parallel to one of its sides. You simply “fill in” the space between the rectangle and the axis of rotation with another rectangle so as to make a larger rectangle of the same height. If the original rectangle is a × b and the filled-in portion is a × c, then the two together will be a × (b + c). The centroid of the original will be at distance c + b/2 from the axis, while the centroid of the one touching the axis of rotation will be at distance c/2 from that axis. The centroid of the two together will be at distance (b + c)/2 from the axis. Applying the original theorem to the two together, we find that the large cylinder is proportional to a parallelepiped with base a × (b + c) and altitude (b + c)/2, while the cylinder generated by the portion of the rectangle touching the axis of rotation is proportional to a parallelepiped with base that is a × c and altitude c/2. Hence the cylindrical annulus generated by the original rectangle, which is a parallelepiped that has base a × b and altitude c + b/2, is proportional to the difference of these two. The rest of the proof is now easy and is left as an exercise, which the reader may do in modern notation.
What is called Pappus' theorem in calculus books—and was known for centuries as Guldin's formula—gives a numerical value for the volume generated by revolving a plane region, namely the product of the area and the circumference of the circle traversed by its centroid during the revolution. In this modern form the theorem was first stated in 1609 by the Swiss astronomer/mathematician Paul Guldin (1577–1643), a Jesuit priest, and published between 1635 and 1640 in the second volume of his four-volume work Centrobaryca seu de centro gravitatis trium specierum quantitatis continuae (The Barycenter, or on the Center of Gravity of the Three Kinds of Continuous Magnitude). It appears to be established that Guldin had not read Pappus and made the discovery independently. He also gave an inadequate proof of the result, and the first actual proof is due to Bonaventura Cavalieri (1598–1647).
The second result stated by Pappus is an immediate application of the Eudoxan theory of proportion, since the volume generated is obviously in direct proportion to the angle of rotation, as are the arcs traversed by individual points.
In this discussion, we have emphasized that Pappus did not write his results in our modern language of formulas for areas and volumes. Would he have understood them if they had been stated to him? Putting the question another way, how close was he to our point of view? Two concepts that he used now strike us as unnecessary complications. The first was the Euclidean style of avoiding the choice of unit lengths, areas, and volumes. This approach required Pappus to talk about the ratio of two solids rather than the volume of a single solid. He could only say, for example, that solids of revolution are proportional to the composite ratio of the planar regions that are revolved to form them and lines from their centers of gravity to the axes of rotation. That means, to us, that the volume of such a solid is a constant times the product of the area of the planar region and the length of the line, the same constant for all solids of revolution. In fact, if the angle formed by the line from the center of gravity of the planar region to the axis of rotation is θ, the constant is 2π sin (θ). The other complicated concept is that of a composite ratio. We have now seen two examples of the application of this concept (the argument just given, and Problem 12.3), and it is clear that if two ratios are regarded as numbers, then the composite ratio corresponds to the product of those two numbers. Did Pappus know either of these things? It is very likely that he did, in a sense, although he may not have thought of the situation in quite those terms. As Cuomo (2000, § 5.1) emphasizes, after giving Euclidean-style arguments to prove his propositions, Pappus illustrated many of them with numerical examples. If he had proved this theorem and illustrated it as he did some others, we would have a clearer idea of the extent to which he anticipated the modern refinement of his theorem. But in any case, he was still confined to the notion of a ratio as being a relationship between two objects of the same kind, and he did not think of it as dividing the measure of one of them by the measure of the other. The quantity we obtain by dividing the distance traveled by the time of travel to get the average speed of travel would not have been a ratio to any ancient Greek, and their discussions of motion were not like those of modern physics.
Figure 18.2 Pappus' general locus theorem. The points A, B, and C are fixed at (0, 0), (90, 0), and (150, 0). Point E is confined to the line −2x + 3y = 120, F is confined to the line −3x + 4y = 60, and E, F, and C are required to be collinear. Then the point D is determined as the intersection of the extensions of the lines AE and BF. The conditions imply that D must lie on the line −86x + 133y = 6120.
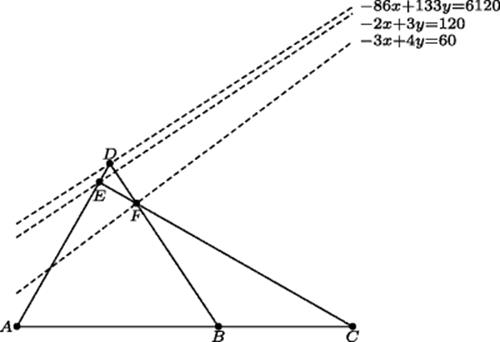
Figure 18.3 Pappus' theorem for two rectangles revolved about an edge. Each of them generates a cylinder whose height equals the side lying on the axis of rotation and whose base has radius equal to the other side. The lines PRand QS are proportional to the perpendicular distances from P and Q to l and m, respectively, so that making them oblique to the axes of rotation does not add any real generality.
18.2 The Later Commentators: Theon and Hypatia
We referred to the later commentators in Chapter 8 as the sources of much of what we know about the history of Greek mathematics. In the present section, we shall say a few words about two of them, namely the fourth-century commentator Theon of Alexandria and his daughter Hypatia, the only woman mathematician of ancient times about whose life a little is known.
18.2.1 Theon of Alexandria
Theon of Alexandria can be dated from the fact that he himself reported that he had observed a solar eclipse on June 16, 364. He continued to write until at least the year 372.
As mentioned above, the tenth-century encyclopedia known as the Suda says that Theon lived in the time of the Emperor Theodosius I (379–395). These dates are therefore consistent. It also states that he worked at the Museum at Alexandria (which contained the Library mentioned earlier), as one of its last members apparently, since it did not survive long after his time.
Theon wrote commentaries on many works, including the Almagest and the works of Euclid. Until a little over a century ago, his edition of Euclid's Elements, on which his daughter Hypatia may have collaborated, was the only known Greek text of the Elements. An earlier edition was discovered in the Vatican in the late nineteenth century. From it, historians can see what original contributions were made by Theon and Hypatia. In particular, we see confirmation of what we said earlier: The editors of ancient works were more interested in improving the work than in preserving it intact. O'Connor and Robertson, writing at the MacTutor website,3 relate that Theon elaborated arguments that were obscure in the earlier manuscripts, adding propositions of his own to clarify them, standardized the notation for certain concepts, and “corrected errors,” which were not always errors but sometimes mere misunderstandings on the part of Theon.
18.2.2 Hypatia of Alexandria
Very few women mathematicians are known by name from early times. However, Closs (1992, p. 12) mentions a Maya ceramic with a picture of a female scribe/mathematician. From ancient Greece and the Hellenistic culture, two or perhaps three such women are known by name. In his Lives of Eminent Philosophers, Diogenes Laertius says that
Pythagoras had a wife named Theano. She was the daughter of Brontinus of Croton, although some say that she was Brontinus' wife and Pythagoras' pupil. He also had a daughter named Damo, as Lysis mentions in a letter to Hipparchus. In this letter he speaks of Pythagoras as follows: ‘And many say that you [Hipparchus] give public lectures on philosophy, as Pythagoras once did. He entrusted his Commentaries to Damo, his daughter, and told her not divulge them to anyone not of their household. And she refused to part with them, even though she could have sold them for a considerable amount of money. . . .’
Since it was said that the Pythagoreans admitted women to their councils, it seems possible that Pythagoras' wife and daughter may have engaged in mathematical research. However, nothing at all is known about any works they may have produced. All that we know about them is contained in the paragraph from Diogenes Laertius just quoted.
There are two primary sources for information about the life of Hypatia. One is a passage in a seven-book history of the Christian Church written by Socrates Scholasticus, who was a contemporary of Hypatia but lived in Constantinople; the other is an article in the Suda. In addition, several letters of Synesius, bishop of Ptolemais (in what is now Libya), who was a student of Hypatia, were written to her or mention her, always in terms of high respect. In one letter he requests her, being in the “big city,” to procure him a scientific instrument (hygrometer) not available in the less urbanized area where he lived. In another he asks her judgment on whether to publish two books that he had written, saying
If you decree that I ought to publish my book, I will dedicate it to orators and philosophers together. The first it will please, and to the other it will be useful, provided of course that it is not rejected by you, who are really able to pass judgment. If it does not seem to you worthy of Greek ears, if, like Aristotle, you prize truth more than friendship, a close and profound darkness will overshadow it, and mankind will never hear it mentioned. [Fitzgerald, 1926]
The account of Hypatia's life written by Socrates Scholasticus occupies Chapter 15 of Book 7 of his Ecclesiastical History. Socrates Scholasticus describes Hypatia as the pre-eminent philosopher of Alexandria in her own time and a pillar of Alexandrian society, who entertained the elite of the city in her home. Among that elite was the Roman procurator Orestes. There was conflict at the time among Christians, Jews, and pagans in Alexandria; Cyril, the bishop of Alexandria, was apparently in conflict with Orestes. According to Socrates, a rumor was spread that Hypatia prevented Orestes from being reconciled with Cyril. This rumor caused some of the more volatile members of the Christian community to seize Hypatia and murder her in March of 415.
The Suda devotes a long article to Hypatia, repeating in essence what was related by Socrates Scholasticus. It says, however, that Hypatia was the wife of the philosopher Isodoros, which is definitely not the case, since Isodoros lived near the end of the fifth century. (He was perhaps the last neo-Platonist in Alexandria.) The Suda assigns the blame for her death to Cyril himself.
Yet another eight centuries passed, and Edward Gibbon came to write the story in his Decline and Fall of the Roman Empire (Chapter XLVII). In Gibbon's version, Cyril's responsibility for the death of Hypatia is reported as fact, and the murder itself is described with certain gory details for which there is no factual basis.
As for her mathematical works, we have already mentioned that she may have been the editor of some of the books of Arithmetica written by Diophantus. From other commentators, it is known that, in addition to her lectures on philosophy, she wrote commentaries on the works of earlier mathematicians.
A fictionalized version of Hypatia's life can be found in a nineteenth-century novel by Charles Kingsley, bearing the title Hypatia, or New Foes with an Old Face. What facts are known were organized into an article by Michael Deakin (1994) and a study of her life by Maria Dzielska (1995).
Problems and Questions
Mathematical Problems
18.1. Prove Pappus' generalization of the Pythagorean theorem, shown in Fig. 18.1, assuming any parallelogram ABΔE whatsoever and any parallelogram BΓZH whatsoever have been constructed on sides AB and BΓ. Extend the outer sides of these two parallelograms to Θ, draw the line ΘB, and extend it to meet AΓ at K. Draw ΓM and AΛ parallel to ΘK, meeting ZH and EΔ in M and Λ respectively. It is easy to see that ΘMΓB and ΘΛAB are parallelograms and that therefore AΛ = BΘ = ΓM. Hence if ΛM is drawn, meeting BK in N, we shall also have KN = BΘ. Then prove that AΓMΛ = ABΔE + BΓZH.
18.2. Explain why Pappus' generalization of the Pythagorean theorem is not merely a trivial consequence of Proposition 31 of Book 6 of the Elements, which states that any similar polygons, similarly situated on the three sides of a right triangle, satisfy the same relation as squares; that is, the sum of the two figures on the legs equals the figure on the hypotenuse.
18.3. Prove Guldin's formula for the union of two regions, given that it is true for each of them. If the centroid of an area A lies at distance r from the axis, and the centroid of another area B disjoint from it lies at distance s from that axis (both areas being on the same side of the axis), then the centroid of the union of the two areas lies at distance ![]() from the axis. (By Archimedes' principle of the lever, this is the distance from the axis to the point at which weights proportional to A and B in the given locations will balance, since it differs from r by
from the axis. (By Archimedes' principle of the lever, this is the distance from the axis to the point at which weights proportional to A and B in the given locations will balance, since it differs from r by ![]() and from s by
and from s by ![]() , distances that are inversely proportional to A and B.) For any plane area that can be approximated from within and without by a union of rectangles, the method of exhaustion then yields the Guldin formula.
, distances that are inversely proportional to A and B.) For any plane area that can be approximated from within and without by a union of rectangles, the method of exhaustion then yields the Guldin formula.
Historical Questions
18.4. Describe some mathematical results that are found in Pappus' Collection.
18.5. For what contributions to mathematics is Theon of Alexandria remembered?
18.6. What position in Alexandrian society did Hypatia have?
Questions for Reflection
18.7. By no means all the conceivable theorems of metric-free plane geometry are found in the works of the authors we have discussed. One that arose in the nineteenth century—known as the Steiner–Lehmus theorem after Jacob Steiner (1796–1863), who proved it, and D. C. L. Lehmus (1780–1863), who posed it—asserts that if two angle bisectors of a triangle are equal, then the triangle is isosceles.4 There are many such results, including, for example, the 1899 discovery by Frank Morley (1860–1937) that the trisectors of the angles of a triangle intersect inside the triangle in three points that are the vertices of an equilateral triangle. Do such results mean that in fact Greek geometry didn't decline at all, that it is still alive and well?
18.8. Sketch out a historical-fiction scenario in which the ancient mathematicians discover analytic geometry through the locus problems discussed by Pappus. To do so, they would have to learn how to interpret a ratio of lines as what we call a real number. Explain how they could have interpreted multiplication and division of such ratios.
18.9. What is meant by saying that Greek geometry was in decline after the time of Apollonius? What did this decline amount to, and how could geometry have been revived?
Notes
1. If one is looking for mathematical explanations of this shape, it would be simpler to start with the assumption that the body of a bee is approximately a cylinder, so that the cells should be approximately cylinders. Now one cylinder can be tightly packed with six adjacent cylinders of the same size. If the cylinders are flexible and there is uniform pressure on them, they will flatten into hexagonal prisms.
2. This principle says that for any two geometric or physical quantities of the same kind, some integer multiple of each is larger than the other. In modern language: Infinitesimals do not exist. The principle is assumed in Euclid's definition of a ratio.
3. http://www-history.mcs.st-and.ac.uk/Biographies/Theon.html
4. This theorem makes a very nice puzzle for the amateur geometer. High-school students sometimes produce very clever proofs of it, but it is deceptively difficult to prove.