The history of mathematics: A brief course (2013)

Part IV. India, China, and Japan 500 BCE-1700 CE

Chapter 21. Brahmagupta, the Kuttaka, and Bhaskara II

The present chapter is devoted to two mathematicians who lived 500 years apart. Of the two, the earlier (Brahmagupta) appears to be by far the more profound and original. Yet the second (Bhaskara II) is also well worth reading—as indeed are many later Hindu mathematicians, like the fifteenth-century Jyesthadeva, whose work we do not have space to discuss.

21.1 Brahmagupta's Plane and Solid Geometry

Brahmagupta devotes five sections of Chapter 12 of the Brahmasphutasiddhanta to geometric results (Colebrooke, 1817, pp. 295–318). Like Aryabhata, he has a practical bent. In giving the common area formulas for triangles and quadrilaterals, he first gives a way of getting a “rough” value for the area: Take the product of the averages of the two pairs of opposite sides. (For this purpose a triangle counts as a quadrilateral having one side equal to zero.) In the days when calculation had to be done by hand, this was a quick approximation that worked well for quadrilaterals and triangles that are nearly rectangular (that is, tall, thin isosceles triangles). He also gave a formula that he says is exact, and this formula is a theorem commonly known as Brahmagupta's theorem: Half the sum of the sides set down four times and severally lessened by the sides, being multiplied together, the square root of the product is the area.In our terms this rule says that the area of a quadrilateral of sides a, b, c, and d is , where s is half of the sum of the lengths of the sides. The case when d = 0, which is a triangle, is what we call Heron's formula and was discussed in Chapter 16. Brahmagupta did not mention the restriction that the quadrilateral must be a cyclic quadrilateral, that is, it must be inscribed in a circle.

Like Aryabhata, Brahmagupta knew that what we are calling one-and two-dimensional π were the same number. In Stanza 40, he says that when the diameter and the square of the radius respectively are multiplied by 3, the results are the “practical” circumference and area. In other words, π = 3 is a “practical” value. He also gives the “neat” (“exact”) value as . Since , this value is not an improvement on Aryabhata's 3.1416 in terms of accuracy. If one had to work with π², it might be more convenient. But π² occurs in very few contexts in mathematics, and none at all in elementary mathematics.

Section 5 of Chapter 12 of the Brahmasphutasiddhanta gives a rule for finding the volume of a frustum of a rectangular pyramid. In keeping with his approach of giving approximate rules, Brahmagupta says to take the product of the averages of the sides of the top and bottom in the two directions, then multiply by the depth. He calls this result the “practical measure” of the volume, and he knew that this simple rule gave a volume that was too small. To see why, imagine a frustum of height h with an a × b rectangle at the top and a proportional rectangle ta × tb at the bottom. The rule just stated would make this volume equal to . Since the true volume is , the difference is times the true volume. So, just as with his rule for triangles, if the pyramid has a very steep slope, so that t is close to 1, this value is reasonably accurate.

For his second approximation, which he called the “rough” volume, he took the average of the areas of the top and bottom and multiplied by the depth.¹ He also knew that this procedure gave a volume that was too large. In terms of the hypothetical frustum just introduced, it gives a volume of , which is larger than the actual volume by of that volume. The actual volume lies between the “practical” volume and the “rough” volume, but where? From the explanation just given, it follows that the actual volume is obtained as a mixture of two parts “practical” and one part “rough.” Brahmagupta's corrective procedure to give the “neat” (exact) volume was: Subtract the practical from the rough, divide the difference by three, and then add the quotient to the practical value. Although this rule seems rather roundabout, it is equivalent to the correct formula. It has some resemblance to the procedure given in the Sulva Sutras for constructing a circle equal to a square, which was discussed in Chapter 20.

21.2 Brahmagupta's Number Theory and Algebra

Brahmagupta's algebra is done entirely in words. For example (p. 279 of the Colebrooke translation), his recipe for the cube of a binomial is as follows:

The cube of the last term is to be set down; and, at the first remove from it, thrice the square of the last multiplied by the preceding; then thrice the square of the preceding term taken into that last one; and finally the cube of the preceding term. The sum is the cube.

In our terms, (a + b)³ = b³ + 3b²a + 3ba² + a³. This rule is used for finding successive approximations to the cube root, just as it was in China, as we shall see in the next two chapters. Similarly, in Section 4 (p. 346 of the Colebrooke translation), he tells how to solve a quadratic equation of the form ax² + bx = c:

Take the absolute number [the constant term c] from the side opposite to that from which the square and simple unknown are to be subtracted. To the absolute number multiplied by four times the [coefficient of the] square, add the square of the [coefficient of the] middle term; the square root of the same, less the [coefficient of the] middle term, being divided by twice the [coefficient of the] square is the [value of the] middle term.

Here the “middle term” is the unknown, and this statement is a very involved description of what we write as the quadratic formula:

Except for extracting cube roots of numbers, Brahmagupta does not consider equations of degree higher than 2.

Brahmagupta gave rules for handling sums of arithmetic progressions. (Aryabhata I had also done this.) He made systematic use of zero and negative numbers, giving the correct rules for manipulating them in the eighteenth chapter of the Brahmasphutasiddhanta. Brahmagupta devotes considerable space to the pulverizer (kuttaka) method of solving linear Diophantine equations, which was mentioned in the preceding chapter. Since this method is worth taking the time to master, we shall discuss it below. Before presenting it, however, we shall first discuss some of his other work in number theory and algebra.

21.2.1 Pythagorean Triples

Brahmagupta gave a method of creating Pythagorean triples of integers. In Chapter 12 of the Brahmasphutasiddhanta (p. 306 of the Colebrooke translation) he gives the rule that the sum of the squares of two unlike quantities are the sides of an isosceles triangle; twice the product of the same two quantities is the perpendicular; and twice the difference of their squares is the base. This rule amounts to the formula (a² + b²)² = (2ab)² + (a² − b²)², but it is stated as if the right triangle has been doubled by gluing another copy to the side of length 2ab, thereby producing an isosceles triangle with base 2(a² − b²), altitude 2ab, and legs each a² + b². The relation stated is a purely geometric relation, showing (in our terms) that the sides and altitude of an isosceles triangle of any shape can be generated by choosing the two lengths a and b suitably. (In our terms, the equations 2(a² − b²) = u and can be solved for a and bgiven any positive numbers u and .)

21.2.2 Pell's Equation

Brahmagupta also considered generalizations of the problem of Pythagorean triples to a more general equation called² Pell's equation and written Dx² − y² + 1 = 0. He gives a recipe for generating a new equation of this form and its solutions from a given solution. The recipe proceeds by starting with two rows of three entries, which we shall illustrate for the case D = 8, which has the solution x = 1, y = 3. We write

The first column contains x, called the lesser solution, the second contains y, called the greater solution, and the third column contains the additive term 1. From these two rows a new row is created whose first entry is the sum of the cross-multiplied first two columns, that is 1 · 3 + 3 · 1 = 6. The second entry is the product of the second entries plus 8 times the product of the first entries, that is 3 · 3 + 8 · 1 · 1 = 17, and the third entry is the product of the third entries. Hence we get a new row 6171, and indeed 8 · 6² + 1 = 289 = 17². In our terms, this says that if 8x² + 1 = y² and , then 8(xv + yu)² + 1 = (8xu + yv)². More generally, Brahmagupta's rule says that if ax² + d = y²and , then

It is easy to verify that this rule is correct using modern algebraic notation. In his book (Weil, 1984), the number theorist André Weil (1906–1998) referred to the relation just written and the more general relation (x² + Ny²)(z² + Nt²) = (xz ± Nyt)² + N(xt yz)² as “Brahmagupta's identity” (his quotation marks).

However this relation was discovered, the motivation for studying it can be plausibly ascribed to a desire to approximate irrational square roots with rational numbers. Brahmagupta's rule with c = d = 1 gives a way of generating larger and larger solutions of the same Diophantine equation ax² + 1 = y². If you have two solutions (x, y) and of this equation, which need not be different, then you have two approximations y/x and for whose squares are, respectively, 1/x² and 1/u² larger than a. The new solution generated will have a square that is only 1/(xv + yu)² larger than a. This aspect of the problem of Pell's equation turns out to have a close connection with its complete solution in the eighteenth century.

21.3 The Kuttaka

Brahmagupta gave a clearer explanation than Aryabhata had done of a method of solving what we call linear Diophantine equations, that is, equations of the form ax = by + c, where a, b, and c are given integers, and x and yunknown integers to be found. He applied this technique to computations involving astronomy and the calendar. We shall illustrate the method with such a computation, not one taken from Brahamgupta's work, but entirely in the spirit of that work.

It is well known that 19 solar years are almost exactly equal to 235 lunar months. Given that the moon was full on January 30, 2010, what is the next year in which it will be full on February 5? If we choose one 235th of a solar year as a unit of time T, so that T ≈ 1.55 days, or 37 hours, 18 minutes, then one year is 235T and according to the fundamental relation, one month is 19T. Since our unit of time T is about a day and a half, the period from January 30 to February 5, which is six days, amounts to 4T, approximately. Thus we would like to find an integer number of years y and an integer number of months x such that

That is, we want x lunar months to exceed y solar years by 4T. Canceling T, we see that we need to solve 19x = 235y + 4. There are infinitely many solutions if there are any at all, since if (x₀, y₀) is a solution, so is (x₀ + 235k, y₀ + 19k) for any integer k whatever. Conversely, any two solutions (x₀, y₀) and (x₁, y₁) will differ by (235k, 19k) for some k. Thus the problem is to find one solution. One way to do this is by trial and error: Just look at multiples of 235 until you find one that leaves a remainder of 15 when divided by 19 (since 15 + 4 = 19). Thus you begin with

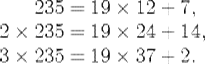
Continuing in this way, you eventually get to 13 × 235 = 19 × 160 + 15 = 19 × 161 − 4, so that 19 × 161 = 13 × 235 + 4. Thus, we can take x = 161, y = 13. In particular, the year will be 2010 + 13 = 2023. (This is correct!) This method of finding a year on which the Moon will be full on a particular date is remarkably accurate, considering that the time period T is actually about 37 hours, and hence not exactly a day and a half. When it goes wrong in a short-term prediction, the moon will be full a day later or earlier in the predicted year.

Thus, the solution of linear Diophantine equations is not difficult. The only disadvantage to the method used above is the tedious trial-and-error procedure of getting one solution. That is where the method called the kuttaka(pulverizer) comes in. This technique shortens the labor of finding the first solution by a considerable amount, especially when the coefficients a, b, and c are large. Here are the steps you follow:

1. First, be sure the equation is written ax = by + c, where a and b are positive, and b > a. In other words, the constant term c needs to be on the same side of the equation as the larger coefficient, and the two coefficients must have the same sign. If they don't, replace y by a new variable z = − y, and then they will have the same sign. You can then multiply the equation by −1 if necessary to get them both positive. The constant term c may be positive or negative. (This “normalizing” is not absolutely essential, but experience shows that one has to be very careful when executing the kuttaka. The experienced user can handle variants in the method, but the beginner had better follow rigid rules.)

2. Second, perform the Euclidean algorithm procedure to find the greatest common divisor d of a and b. If it is larger than 1, then the expression ax − by can only be a multiple of that greatest common divisor, so if c is not a multiple of it, there are no solutions, and you are finished.

3. If d divides c, take all of the quotients—except the last one, which yields a remainder of 0—and write them in a column. To illustrate with the equation 19x = 235y + 4, which we considered above, we have the column

4. Next, augment that column with two more numbers at the bottom. The first one is c/d if the number of quotients is even and −c/d if it is odd. In our case, we have an even number of quotients, and so we adjoin 4 at the bottom. The second additional number, which forms the bottom row of the array, is always 0. Thus we get the following column:

5. Now operate on this column, at each stage modifying the bottom entry and the entry two rows above it, as follows: The entry two rows above the bottom gets replaced by its product with the number below it, plus the number below that. Thus in this example, the first thing to do is to replace the 2 in the third row (counting the bottom row as row 1) by 2 × 4 + 0 = 8. The second part of the procedure is to erase the bottom number. Repeating this procedure until there are only two rows left yields

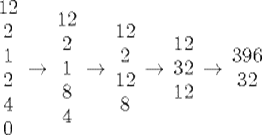
We should now have a solution, and indeed we do: x = 396, y = 32. It is not the smallest solution, however. We get a smaller one by subtracting 235 from x and 19 from y, yielding x = 161, y = 13.

This procedure needs to be practiced on some simple equations, such as 3x = 23y + 1 and 17x = 11y − 5, before the details will fall into place. The number of errors that can creep into this procedure is rather large. If the answer you get doesn't check when you put the values of x and y back into the equation, look for the following possible mistakes:

1. a and b must both be positive and their greatest common divisor d must also divide c if the equation is to have any solutions.

2. When the equation is written ax = by + c, you must have b > a.

3. Do not include the last quotient from the Euclidean algorithm in the column.

4. Adjoin c/d to the column of quotients (ignore the remainders in this algorithm), if you have an even number of quotients. (If c/d is negative, leave it negative in this case.) If the number of quotients is odd, adjoin −c/d. (If c/dis negative, make it positive in this case.)

These are the commonest sources of errors when carrying out this procedure. But of course, you also have to do the divisions with remainder carefully, avoiding computational errors.

21.4 Algebra in the Works of Bhaskara II

The Lilavati of Bhaskara II contains a collection of problems in algebra, which are sometimes stated as though they were intended purely for amusement. For example,

One pair out of a flock of geese remained sporting in the water, and saw seven times the half of the square-root of the flock proceeding to the shore, tired of the diversion. Tell me, dear girl, the number of the flock.

Like countless other unrealistic algebra problems that have appeared in textbooks over the centuries, this story is a way of posing to the student a specific quadratic equation, namely , whose solution is x = 16.

21.4.1 The Vija Ganita (Algebra)

As mentioned in Chapter 19, Bhaskara II advertised his Algebra as an object of intellectual contemplation. We may agree that it fits this description. The problems, however, are just as fanciful as in the Lilavati. For example, the rule for solving quadratic equations is applied in the Vija Ganita (p. 212 of the Colebrooke translation) to find the number of arrows x that Arjuna (hero of the Mahabharata) had in his quiver, given that he shot them all, using to deflect the arrows of his antagonist, to kill his antagonist's horse, six to kill the antagonist himself, three to demolish his antagonist's weapons and shield, and one to decapitate him. In other words, .

21.4.2 Combinatorics

Bhaskara gives a thorough treatment of permutations and combinations, which already had a long history in India. He describes combinatorial formulas such as

by saying

Let the figures from one upward, differing by one, put in the inverse order, be divided by the same in the direct order; and let the subsequent be multiplied by the preceding and the next following by the foregoing. The several results are the changes by ones, twos, threes, etc.

He illustrates this principle by asking how many possible combinations of stressed and unstressed syllables there are in a six-syllable verse. His solution is as follows:

The figures from 1 to 6 are set down, and the statement of them, in direct and inverse order is

The results are: changes with one long syllable, 6; with two 15; with three, 20; with four, 15, with five, 6; with all long, 1.

Bhaskara assures the reader that the same method can be used to find the permutations of all varieties of meter. He then goes on to develop some variants of this problem, for example,

A number has 5 digits and the sum of the digits is 13. If zero is not a digit, find the total number of possible numbers.

To solve this problem, you have to consider the possibility of two distinct digits (for example, 91111, 52222, 13333, 55111, 22333), three distinct digits (for example 82111, 73111) and count all the possible rearrangements of the digits.

Bhaskara reports that the initial syllables of the names for colors “have been selected by venerable teachers for names of values of unknown quantities, for the purpose of reckoning therewith.” He proceeds to give the rules for manipulating expressions involving such quantities; for example, the rule that we would write as (− x − 1) + (2x − 8) = x − 9 is written

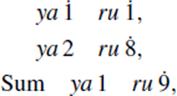
where the dots indicate negative quantities. The syllable ya is the first syllable of the word for black, and ru is the first syllable of the word for species.

Bhaskara gives the rule that we express as the quadratic formula for solving a quadratic equation by radicals, then goes on to give a criterion for a quadratic equation to have two (positive) roots. He also says (pp. 207–208 of the Colebrooke translation) that “if the solution cannot be found in this way, as in the case of cubic or quartic equations, it must be found by the solver's own ingenuity.” That ingenuity includes some work that would nowadays be regarded as highly inventive, not to say suspect; for example (p. 214), Bhaskara's solution of the equation

Bhaskara warns that multiplying by zero does not make the product zero, since further operations are to be performed. Then he simply cancels the zeros, saying that, since the multiplier and divisor are both zero, the expression is unaltered. The result is the equation we would write as . Bhaskara clears the denominator and writes the equivalent of 9x² + 12x = 60. Even if the multiplication by zero is interpreted as multiplication by a nonzero expression that is tending to zero, as a modern mathematician would like to do, this cancelation is not allowed, since the first term in the numerator is a higher-order infinitesimal than the second. Bhaskara is handling 0 here as if it were 1. Granting that operation, he does correctly deduce, by completing the square (adding 4 to each side), that x = 2.

Bhaskara says in the Vija Ganita that a nonzero number divided by zero gives an infinite quotient.

This fraction , of which the denominator is cipher, is termed an infinite quantity. In this quantity consisting of that which has cipher for its divisor, there is no alteration, though many be inserted or extracted; as no change takes place in the infinite and immutable GOD [Vishnu], at the period of the destruction or creation of worlds, though numerous orders of beings are absorbed or put forth.

By the time of Bhaskara, the distinction between a rational and an irrational square root was well known. The Sanskrit word for an irrational root is carani, according to the commentator Krishna (Plofker, 2009, p. 145), who defines it as a number, “the root of which is required but cannot be found without residue.” Bhaskara gives rules such as and .

21.5 Geometry in the Works of Bhaskara II

In his work Siddhanta Siromani (Crest Jewel of the Siddhantas), written in 1150, Bhaskara tackled the extremely difficult problem of finding the area of a sphere. As we have seen (Section 7.2 of Chapter 7), the Egyptians had deduced correctly that the area of a hemisphere is twice the area of its circular base, and (Section 14.2 of Chapter 14) Archimedes had proved rigorously that the surface of a sphere is four times the equatorial disk it contains. In order to achieve that result, Archimedes had to make use of the method of exhaustion, which can be seen as an anticipation of integral calculus. Something similar can be said about Bhaskara's approach, which was numerical and based on Aryabhata's trigonometry, in contrast to the metric-free approach used by Archimedes. The discussion we are about to give is based on the exposition of this result given by Plofker (2009, pp. 196–201).

As was stated in the previous chapter, in constructing his table of sine differences, Aryabhata I chose 225' of arc as the constant difference, dividing the arc of one quadrant of a circle of radius 3438' into 24 equal pieces. Bhaskara II started from that point, dividing a complete great circle of a sphere—which we can think of as the equator—into 96 equal pieces. Each of these pieces is regarded as one unit of length. He then imagined the lines of longitude drawn through these 96 points running from pole to pole, thereby partitioning the sphere into 96 mutually congruent sectors. In each sector, he then imagined the circles of latitude drawn, dividing each quadrant of a line of longitude into 24 equal arcs between the pole and the equator, 48 between the two poles. Thus the surface of the sphere was partitioned into 96 × 48 = 4608 regions, 192 of which (those having a vertex at one of the poles) are curvilinear triangles, and the other 4416 of which are curvilinear trapezoids. A set of 20 of these trapezoids lying just above the equator is shown in Fig. 21.1. Since they are very small, one can imagine that they actually are planar triangles and trapezoids. For a typical trapezoid whose upper and lower edges are at co-latitudes (k − 1) × 225' and k × 225'—these are the distances along a line of longitude from the pole—the lengths of these edges are proportional to the radii of those circles of latitude. In terms of the unit of length (1') chosen by Aryabhata, the radius r of the circle at co-latitude k × 225' is sin (k × 225'); that is, it is given in the second column of the table of sines displayed in the previous chapter. The length of the arc of that circle inside the sector is 225'. However, these are minutes of arc on the circle of latitude, not on the sphere. A minute of arc on a circle of radius r is minutes of arc on a great-circle of a sphere of radius R. Thus, the portion of the circle of latitude of radius r inside each sector has length minutes of spherical arc, where R = 3438. Since Bhaskara's unit of length is 225 of Aryabhata's units, we need to divide by 225. Altogether then, the length of that arc inside a given sector at co-latitude k × 225' is . The area of each trapezoid (again, treated as if it were a plane trapezoid) is numerically equal to the average of these lengths for the upper and lower edges, since each trapezoid has altitude equal to one unit. All we have to do then is sum up the areas of the 4416 trapezoids and the 192 triangles in order to find the area of the sphere. This is done most easily by finding the area of a half-sector and doubling it. To find the area of each triangle or trapezoid between the pole and the equator in a given sector, one has only to take the average of the lengths of the opposite sides (counting the “side” at the pole as having length 0), multiply by the altitude, and then add up the results. Thus, we need to find

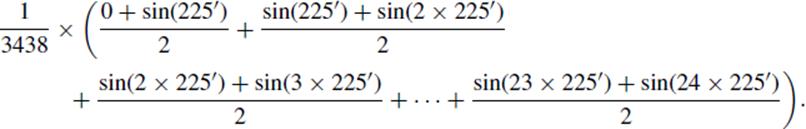
Figure 21.1 Bhaskara's “polygonal” method of getting the area of a sphere.

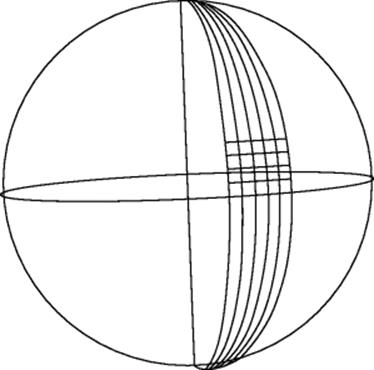
Bhaskara saw how this sum could be rewritten to eliminate the 2 in each denominator, except for the very last term. He evaluated it by adding up all of the sines in the table and then subtracting half of the last one. This was a simple exercise in arithmetic, and we noted in the previous chapter that the sines in the table add up to 54, 233. Therefore, the area of a half-sector is numerically

(The number 1719 is half of the sine of a 90° arc.) A full sector is then twice this amount, or 30.54916. Bhaskara observed that this is, within the limits of precision, precisely the diameter of the sphere, since . Thus, it seems that if a sphere is partitioned into sectors of unit opening, the area of each sector in square units is numerically equal to the length of the diameter. Since the total area of the sphere is 96 times the area of this sector—that is, it is this area times the number of units of length in the circumference, Bhaskara concluded (correctly) that the area of a sphere [in square units] is equal to its diameter times its circumference. Bhaskara would have had to construct a finer table of sines in order to test the result with a smaller unit of length (by partitioning the sphere into more than 4608 regions). As a practical matter, since the actual diameter is about 0.01 units larger than the value he used, while he had the circumference correct, he would have gotten a numerical value for the area that is too small by 1%. In our terms, his unit of area was , and the numerical approximation that he used for the area was

where

The accurate value of c_n would be 4. Bhaskara's procedure amounts to taking n = 24. By direct computation, we get c₂₄ ≈ 3.96023, which is, as already noted, 1% too small.

That Bhaskara understood the principle of infinitesimal approximation is shown by another of his results, in which he says that the difference between two successive sines in the table, that is, sin ((k + 1) × 225') − sin (k × 225'), is 225 cos (k × 225')/R (where R = 3438). This result seems to prefigure the infinitesimal relation that calculus books write as

Problems and Questions

Mathematical Problems

21.1 Given the Pell equation y² − 11x² = 1, which has solutions x = 3, y = 10 and x = 60, y = 199, construct a third solution and use it to get an approximation to .

21.2 Solve Bhaskara's problem of finding the number of positive integers having five nonzero digits whose sum is 13.

21.3 Use the kuttaka to solve the equation 24x = 57y + 15. Find the smallest positive integers x and y that satisfy this equation.

Historical Questions

21.4 How accurate are the rules given by Brahmagupta for computing areas and volumes?

21.5 What topics in number theory not discussed by Euclid and Nicomachus can be found in the works of Hindu mathematicians?

21.6 How did Bhaskara II treat division by zero?

Questions for Reflection

21.7 How practical was it to use the kuttaka to compute the dates of future conjunctions of the heavenly bodies (for example, eclipses)? Does this technique yield accurate and reliable results? What might go wrong in a given practical application?

21.8 What justification does Bhaskara II offer for the problems in the Lilavati? Does he live up to his advertising?

21.9 Compare the trigonometries developed by Ptolemy and the Hindu mathematicians with each other and with trigonometry as we know it today. What significant differences are there between any two of them?

Notes

1. This is the same procedure followed in the cuneiform tablet BM 85194, discussed above in Section 5.3 of Chapter 5.

2. Erroneously so-called, according to Dickson (1920, p. 341), who asserts that Fermat had studied the equation earlier than John Pell (1611–1685). However, the MacTutor website at the University of St Andrews gives evidence that Euler's attribution of this equation to Pell was accurate. Everybody agrees that the solutions of the equation were worked out by Joseph-Louis Lagrange (1736–1813), not Pell.