The history of mathematics: A brief course (2013)

Part IV. India, China, and Japan 500 BCE-1700 CE

Chapter 22. Early Classics of Chinese Mathematics

The name China refers to a region unified under a central government but whose exact geographic extent has varied considerably over the 4000 years of its history. To frame our discussion, we shall sometimes refer to the following dynasties:

1. The Shang Dynasty (sixteenth to eleventh centuries bce). The Shang rulers controlled the northern part of what is now China and had an extensive commercial empire.

2. The Zhou Dynasty (eleventh to eighth centuries bce). The Shang Dynasty was conquered by people from the northwest known as the Zhou. The great Chinese philosophers known in the West as Confucius, Mencius, and Lao-Tzu lived and taught during the several centuries of disorder that came after the decay of this dynasty.

3. The Period of Warring States (403–221 BCE) and the Qin Dynasty (221–206 BCE). Warfare was nearly continuous in the fourth and third centuries BCE, but in the second half of the third century the northwestern border state of Qin gradually defeated all of its rivals and became the supreme power under the first Qin emperor. The name China is derived from the Qin.

4. The Han Dynasty (206 BCE –220 ce). The empire was conquered shortly after the death of the Qin emperor by people known as the Han, who expanded their control far to the south, into present-day Viet Nam, and established a colonial rule in the Korean peninsula. Contact with India during this dynasty brought Buddhism to China for the first time. According to Mikami (1913, pp. 57–58), mathematical and astronomical works from India were brought to China and studied. Certain topics, such as combinatorics, are common to both Indian and Chinese treatises, but “there is nothing positive that serves as an evidence of any actual Indian influence upon the Chinese mathematics.”

5. The Tang Dynasty (seventh and eighth centuries). The Tang Dynasty was a period of high scholarship, in which, for example, block printing was invented.

6. The Song Dynasty (960–1279). The period of disorder after the fall of the Tang Dynasty ended with the accession of the first Song emperor. Confucianism underwent a resurgence in this period, supplementing its moral teaching with metaphysical speculation. Scientific treatises on chemistry, zoology, and botany were written, and the Chinese made great advances in algebra.

7. The Mongol conquest and the closing of China. The Song Dynasty was ended in the thirteenth century by the Mongol conquest under the descendants of Genghis Khan, whose grandson Kublai Khan was the first emperor of the dynasty known in China as the Yuan. As the Mongols were Muslims, this conquest brought China into contact with the intellectual achievements of the Muslim world. Knowledge flowed both ways, and the sophisticated Chinese methods of root extraction seem to be reflected in the works of later Muslim scholars, such as the fifteenth-century mathematician al-Kashi. The vast Mongol Empire facilitated East–West contacts, and it was during this period that Marco Polo (1254–1324) made his famous voyage to the Orient.

8. The Ming Dynasty (fourteenth to seventeenth centuries). While the Mongol conquest of Russia lasted 240 years, the Mongols were driven out of China in less than a century by the first Ming emperor. During the Ming Dynasty, Chinese trade and scholarship recovered rapidly. The effect of the conquest, however, was to encourage Chinese isolationism, which became the official policy of the later Ming emperors during the period of European expansion. The first significant European contact came in the year 1582, when the Italian Jesuit priest Matteo Ricci (1552–1610) arrived in China. The Jesuits were particularly interested in bringing Western science to China to aid in converting the Chinese to Christianity. They persisted in these efforts despite the opposition of the emperor. The Ming Dynasty ended in the mid-seventeenth century with conquest by the Manchus.

9. The Ching (Manchu) Dynasty (1644–1911). After two centuries of relative prosperity the Ching Dynasty suffered from the depredations of foreign powers eager to control its trade. Perhaps the worst example was the Opium War of 1839–1842, fought by the British in order to gain control of the opium trade. From that time on, Manchu rule declined. In 1900, the Boxer Rebellion against the Western occupation was crushed and the Chinese were forced to pay heavy reparations. In 1911 the government disintegrated entirely, and a republic was declared.

10. The twentieth century. The establishment of a republic in China did not quell the social unrest, and there were serious uprisings for several decades. China suffered badly from World War II, which began with a Japanese invasion in the 1930s. Although China was declared one of the major powers when the United Nations was formed in 1946, the Communist revolution of 1949 drove its leader Chiang Kai-Shek to the island of Taiwan. China is now engaged in extensive cultural and commercial exchanges with countries all over the world and hosted the International Congress of Mathematicians in 2002. Its mathematicians have made outstanding contributions to the advancement of mathematics, and Chinese students are welcomed at universities in nearly every country.

22.1 Works and Authors

Mathematics became a recognized and respected area of intellectual endeavor in China more than 2000 years ago. That its origins are at least that old is established by the existence of books on mathematics, at least one of which was probably written before the order of the Emperor Shih Huang-Ti in 213 BCE that all books be burned.¹ A few books survived or were reconstituted after the brief reign of Shih Huang-Ti, among them the mathematical classic just alluded to. This work and three later ones now exist in English translation, with commentaries to provide the proper context for readers who are unfamiliar with the history and language of China. Under the Tang dynasty, a standardized educational system came into place for the training of civil servants, based on literary and scientific classics, and the works listed below became part of a mathematical curriculum known as the Suan Jing Shishu (Ten Canonical Mathematical Classics—there are actually 12 of them). Throughout this long period, mathematics was cultivated together with astronomy both as an art form and for practical application in the problem of obtaining an accurate lunisolar calendar. In addition, many problems of commercial arithmetic and civil administration appear in the classic works.

22.1.1 The Zhou Bi Suan Jing

The early treatise alluded to above, the Zhou Bi Suan Jing, has been known in English as the Arithmetic Classic of the Gnomon and the Circular Paths of Heaven. A recent study and English translation has been carried out by Christopher Cullen of the University of London (1996). According to Cullen, the title Zhou Bi could be rendered as Gnomon of the Zhou. The phrase suan jing occurs in the titles of several early mathematical works; it means mathematical treatise or mathematical manual. According to a tradition, the Zhou Bi Suan Jing was written during the Western Zhou dynasty, which overthrew the earlier Shang dynasty around 1025 BCE and lasted until 771 BCE. Experts now believe, however, that the present text was put together during the Western Han dynasty, during the first century BCE, and that the commentator Zhao Shuang, who wrote the version we now have, lived during the third century CE, after the fall of the Han dynasty. However, the astronomical information in the book could only have been obtained over many centuries of observation and therefore must be much earlier than the writing of the treatise.

As the traditional title shows, the work is concerned with astronomy and surveying. The study of astronomy was probably regarded as socially useful in two ways: (1) It helped to regulate the calendar, a matter of great importance when rituals were to be performed; (2) it provided a method of divination (astrology), also of importance both for the individual and for the state. Surveying is of use in any society where it is necessary to erect large structures such as dams and bridges and where land is often flooded, requiring people to abandon their land holdings and reclaim them later.

These applications make mathematics useful in practice. However, the preface, written by the commentator Zhao Shuang, gives a different version of the motive for compiling this knowledge. Apparently a student of traditional Chinese philosophy, he had realized that it was impossible to understand fully all the mysteries of the changing universe. He reports that he had looked into this treatise while convalescing from an illness and had been so impressed by the acuity of the knowledge it contained that he decided to popularize it by writing commentaries to help the reader over the hard parts, saying, “Perhaps in time, gentlemen with a taste for wide learning may turn their attention to this work” (Cullen, 1996, p. 171). Here we see mathematics being praised simply because it confers understanding where ignorance would otherwise be; it is regarded as one of the liberal arts, to be studied by a leisured class of gentlemen scholars, people fortunate enough to be free of the daily grind of physical labor that was the lot of the majority of people in all countries until very recent times.

22.1.2 The Jiu Zhang Suan Shu

Another ancient Chinese treatise, the Jiu Zhang Suan Shu, meaning Nine Chapters on the Mathematical Art,² has been partly translated into English, with commentary, by Lam (1994). A corrected and commented edition was published in Chinese in 1992, assembled by Guo (1992). This work has been called the classic Chinese mathematical treatise, since commentaries were written on it for centuries, and it had a large influence on the development of mathematics in Korea and Japan. It reflects the state of mathematics in China in the later Han dynasty, around the year 100 CE. The nine chapters that give this monograph its name contain 246 applied problems of a sort useful in teaching how to handle arithmetic and elementary algebra and how to apply them in commercial and administrative work. In that respect, it offers many parallels with the Rhind papyrus. The nine chapters have no prefaces in which the author explains their purpose, and so we must assume that the purpose was the obvious one of training people engaged in surveying, administration, and trade. Some of the problems are practical, explaining how to find areas, convert units of length and area, and deal with fractions and proportions. Yet when we analyze the algebraic parts of this work, we shall see that it contains impractical puzzle-type problems leading to systems of linear equations and resembling problems that have filled up algebra books for centuries. Such problems are apparently intended to train the mind in algebraic thinking.

22.1.3 The Sun Zi Suan Jing

Another early treatise, the Sun Zi Suan Jing or Mathematical Classic of Sun Zi, was written several centuries after the Jiu Zhang Suan Shu. This work begins with a preface praising the universality of mathematics for its role in governing the lives of all creatures and placing it in the context of Chinese philosophy and among the six fundamental arts (decorum, music, archery, charioteership, calligraphy, and mathematics).

The preface makes it clear that mathematics is appreciated both as a practical skill in life and as an intellectual endeavor. The practicality comes in the use of compasses and gnomons for surveying and in the use of arithmetic for computing weights and measures. The intellectual skill, however, is emphasized. Mathematics is valued because it trains the mind. “If one neglects its study, one will not be able to achieve excellence and thoroughness” (Lam and Ang, 1992, p. 151).

As in the quotation from the commentary on the Zhou Bi Suan Jing, we find that an aura of mystery and “elitism” surrounds mathematics. It is to be pursued by a dedicated group of initiates, who expect to be respected for learning its mysteries, as theologians were during the Middle Ages in the West. At the same time, mathematics has a practical value that is also respected.

22.1.4 Liu Hui. The Hai Dao Suan Jing

The fall of the Han Dynasty in the early third century gave rise to three separate kingdoms in the area now known as China. The north-central kingdom is known as the Kingdom of Wei. There, in the late third century ce, a mathematician named Liu Hui (ca. 220–280) wrote a commentary on the final chapter of the Jiu Zhang Suan Shu. This chapter is devoted to the theorem we know as the Pythagorean theorem, and Liu Hui's book, the Hai Dao Suan Jing (Sea Island Mathematical Classic), shows how to use pairs of similar right triangles to measure inacessible distances. The name of the work comes from the first problem in it, which is to find the height of a mountain on an offshore island and the distance to the base of the mountain. The work consists of nine problems in surveying that can be solved by the algebraic techniques practiced in China at the time. A translation of these problems, a history of the text itself, and commentary on the mathematical techniques can be found in the paper by Ang and Swetz (1986).

22.1.5 Zu Chongzhi and Zu Geng

According to Li and Du (1987, pp. 80–82), fifth-century China produced two outstanding mathematicians, father and son. Zu Chongzhi (429–501) and his son Zu Geng (ca. 450–520) were geometers who used a method resembling what is now called Cavalieri's principle for calculating volumes bounded by curved surfaces. The elder Zu was also a numerical analyst, who wrote a book on approximation entitled Zhui Shu (Method of Interpolation), which became for a while part of the classical curriculum. However, this book was apparently regarded as too difficult for nonspecialists, and it was dropped from the curriculum and lost. Zu Geng continued working in the same area as his father and had a son who also became a mathematician.

22.1.6 Yang Hui

We now leave a considerable (700-year) gap in the story of Chinese mathematics and come to Yang Hui (ca. 1238–1298), the author of a number of mathematical texts. According to Li and Du (1987, pp. 110, 115), one of these was Xiangjie Jiuzhang Suan Fa (Detailed Analysis of the Mathematical Rules in the Jiu Zhang Suan Shu), a work of 12 chapters, one on each of the nine chapters of the Jiu Zhang Suan Shu, plus three more containing other methods and more advanced analysis. In 1274 and 1275 he wrote two other works, which were later collected in a single work called the Yang Hui Suan Fa (Yang Hui's Computational Methods). In these works he discussed not only mathematics but also its pedagogy, advocating real understanding over rote learning.

22.1.7 Cheng Dawei

In the later Ming dynasty, a governmental administrator named Cheng Dawei (1533–1606) applied his mind to the solution of problems using the abacus. In 1592 he wrote a book entitled Suan Fa Tong Zong (General Source of Computational Methods), containing nearly 600 problems on a huge variety of topics, including magic squares and even more arcane subjects.

22.2 China's Encounter with Western Mathematics

Jesuit missionaries who entered China during the late sixteenth century brought with them some mathematical works, including Euclid's Elements, the first six books of which the missionary Matteo Ricci and the Chinese scholar Xu Guangchi (1562–1633) translated into Chinese (Li and Du, 1987, p. 193). The version of Euclid that they used, a Latin translation by the German Jesuit Christopher Clavius (1538–1612) bearing the title Euclidis elementorum libri XV (The Fifteen Books of Euclid's Elements), is still extant, preserved in the Beijing Library. This book aroused interest in China because it was the basis of Western astronomy and therefore offered a new approach to the calendar and to the prediction of eclipses. According to Mikami (1913, p. 114), the Western methods made a correct prediction of a solar eclipse in 1629, which traditional Chinese methods got wrong. It was this accurate prediction that attracted the attention of Chinese mathematicians to Euclid's book, rather than the elaborate logical structure which is its most prominent distinguishing characteristic. Martzloff (1993) studied a commented (1700) edition of Euclid by the mathematician Du Zhigeng and noted that it was considerably abridged, omitting many proofs of propositions that are visually or topologically obvious. As Martzloff says, although Du Zhigeng retained the logical form of Euclid—that is, the definitions, axioms, postulates, and propositions—he neglected proofs, either omitting them entirely or giving only a fraction of a proof, “a fraction not necessarily containing the part of the Euclidean argument relevant to a given proposition and devoted to the mathematical proof in the proper sense of the term.” Du Zhigeng also attempted to synthesize the traditional Chinese classics, such as the Jiu Zhang Suan Shu and the Suan Fa Tong Zong, with works imported from Europe, such as Archimedes' treatise on the measurement of the circle. Thus in China, Western mathematics supplemented, but did not replace, the mathematics that already existed.

The first Manchu Emperor Kang Xi (1654–1722) was fascinated by science and insisted on being taught by two French Jesuits, Jean-François Gerbillon (1654–1707) and Joachim Bouvet (1656–1730), who were in China in the late 1680s. This was the time of the Sun King, Louis XIV, who was vying with Spain and Portugal for influence in the Orient. The two Jesuits were required to be at the palace from before dawn until long after sunset and to give lessons to the Emperor for four hours in the middle of each day (Li and Du, 1987, pp. 217–218).

Given the increasing contacts between East and West in the nineteenth century, some merging of ideas was inevitable. During the 1850s the mathematician Li Shanlan (1811–1882), described by Martzloff (1982) as “one of the last representatives of Chinese traditional mathematics,” translated a number of contemporary works into Chinese, including an 1851 calculus textbook of the American astronomer–mathematician Elias Loomis (1811–1889) and an algebra text by Augustus De Morgan (1806–1871). Li Shanlan had a power over formulas that reminds one in many ways of the twentieth-century Indian genius Srinivasa Ramanujan. One of his combinatorial formulas, stated without proof in 1867, was finally proved through the ingenuity of the prominent Hungarian mathematician Paul Turán (1910–1976). By the early twentieth century, Chinese mathematical schools had marked out their own territory, specializing in standard areas of mathematics such as analytic function theory. Despite the difficulties of war, revolution, and a period of isolation during the 1960s, transmission of mathematical literature between China and the West continued and greatly expanded through exchanges of students and faculty from the 1980s onward. Kazdan (1986) gives an interesting snapshot of the situation in China at the beginning of this period of expansion.

22.3 The Chinese Number System

In contrast to the Egyptians, who computed with ink on papyrus, the ancient Chinese, starting in the time of the Shang Dynasty, used rods representing numerals to carry out computations. Chinese documents from the second century BCE mention the use of counting rods, and a set of such rods from the first century BCE was discovered in 1970. The rods can be arranged to form the Shang numerals (Fig. 22.1) and thereby represent decimal digits. They were used in conjunction with a counting board, which is a board ruled into squares so that each column (or row, depending on the direction of writing) represents a particular item. In pure computations, the successive rows in the board indexed powers of 10. These rods could be stacked to represent any digit from 1 to 9. Since they were placed on a board in rows and columns, the empty places are logically equivalent to a use of 0, but not psychologically equivalent. The use of a circle for zero in China is not found before the thirteenth century. On the other hand, according to Lam and Ang (1987, p. 102), the concept of negative numbers (fu), represented by black rods instead of the usual red ones for positive numbers (cheng), was also present as early as the fourth century BCE.

Figure 22.1 The Shang numerals.

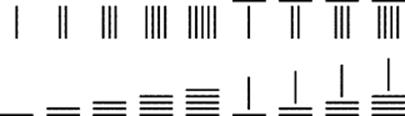
It is difficult to distinguish between, say, 22 (|| ||) and 4 (||||) if the rods are placed too close together. To avoid that difficulty, the Chinese rotated the rods in alternate rows through a right angle, in effect using a positional system based on 100 rather than 10. Since this book is being published in a language that is read from left to right, then from top to bottom, we shall alternate columns rather than rows. In our exposition of the system the number 22 becomes and 4 remains ||||. The Shang numerals are shown in Fig. 22.1, the top row being used to represent digits multiplied by an even power of 10 and the bottom row representing digits multiplied by an odd power of 10.

22.3.1 Fractions and Roots

The Sun Zi Suan Jing gives a procedure for reducing fractions that is equivalent to the familiar Euclidean algorithm for finding the greatest common divisor of two integers. The rule is to subtract the smaller number from the larger until the difference is smaller than the originally smaller number. Then begin subtracting the difference from the smaller number. Continue this procedure until two equal numbers are obtained. That number can then be divided out of both numerator and denominator.

With this procedure for reducing fractions to lowest terms, a complete and simple theory of computation with fractions is feasible. Such a theory is given in the Sun Zi Suan Jing, including the standard procedure for converting a mixed number to an improper fraction and the procedures for adding, subtracting, multiplying, and dividing fractions. Thus, the Chinese had complete control over the system of rational numbers, including, as we shall see below, the negative rational numbers.

At an early date the Chinese dealt with roots of integers, numbers like , which we now know to be irrational; and they found mixed numbers as approximations when the integer is not a perfect square. In the case of , the approximation would have been given as . (The denominator is always twice the integer part, as a result of the approximation used. As with the Hindus and others, the basic principle is that .)

22.4 Algebra

Sooner or later, constantly solving problems of more and more complexity in order to find unknown quantities leads to the systematization of ways of imagining operations performed on a “generic” number (unknown). When the point arises at which an unknown or unspecified number is described by some of its properties rather than explicitly named, we may say that algebra has arisen. There is a kind of twilight zone between arithmetic and algebra, in which certain problems are solved imaginatively without using symbols for unknowns, but later are seen to be easily solvable by the systematic methods of algebra. An example of such a problem is the one from the Bakshali manuscript discussed in Chapter 20 asking for the relative prices of draft horses, thoroughbred horses, and camels.

A good example from China is Problem 15 of Chapter 3 of the Sun Zi Suan Jing, which asks how many carts and how many people are involved, given that there are two empty carts (and all the others are full) when people are assigned three to a cart, but nine people have to walk if only two are placed in each cart. We would naturally make this a problem in two linear equations in two unknowns: If x is the number of people and y the number of carts, then

However, that would be using algebra, and Sun Zi does not quite do that in this case. His solution is as follows:

Put down 2 carts, multiply by 3 to give 6, add 9, which is the number of persons who have to walk, to obtain 15 carts. To find the number of persons, multiply the number of carts by 2 and add 9, which is the number of persons who have to walk.

Probably the reasoning in the first sentence here is pictorial. Imagine each cart filled with three people. When loaded in this way, the carts would accommodate all the “real” people in the problem, plus six “fictitious” people, since we are given that two carts would be empty if the others each carried three people. Let us imagine, then, that six fictitious people are added to the passengers, one in each of six carts, each of which therefore contains two real people and one fictitious person, while each of the others contains three real people. Now imagine one person removed from each cart, preferably a fictitious person if possible. The number of people removed would obviously be equal to the number of carts. The six fictitious people would then be removed, along with the nine real people who have to walk when there are only two people in each cart. It follows that there must be 15 carts. Finding the number of people (39) is straightforward once the number of carts is known.

The nature of divisibility for integers is also studied in the Sun Zi Suan Jing, which contains the essence of the result still known today as the Chinese remainder theorem. The problem asks for a number that leaves a remainder of 2 when divided by 3, a remainder of 3 when divided by 5, and a remainder of 2 when divided by 7. The fact that any number of such congruences can be solved simultaneously if the divisors are all pairwise relatively prime is the content of what we know now as the Chinese remainder theorem. According to Dickson (1920, p. 57), this name arose when the mathematically literate British missionary Alexander Wylie (1815–1887) wrote an article on it in the English-language newspaper North China Herald in 1852. By that time the result was already known in Europe, having been discovered by Gauss and published in his Disquisitiones arithmeticæ (Art. 36) in 1836.

Sun Zi's answer to this problem shows that he knew a general method of proceeding. He says, “Since the remainder on division by 3 is 2, take 140. The remainder on division by 5 is 3, so take 63. The remainder on division by 7 is 2, so take 30. Add these numbers, getting 233. From this subtract 210, getting the answer as 23.” In other words, he took the smallest multiple of 5 · 7 that leaves a remainder of 2 when divided by 3, then the smallest multiple of 3 · 7 that leaves a remainder of 3 when divided by 5, and then the smallest multiple of 3 · 5 that leaves a remainder of 2 when divided by 7. The sum of these numbers was bound to satisfy all three congruences, and then he could add or subtract an arbitrary multiple of 3 · 5 · 7.

22.5 Contents of the Jiu Zhang Suan Shu

This classic work assumes that the methods of calculation explained in the Sun Zi Suan Jing are known and applies them to problems very similar to those discussed in the Rhind papyrus. In fact, Problems 5, 7, 10, and 15 from the Chapter 1 of the Jiu Zhang Suan Shu are reprinted at the beginning of Chapter 2 of the Sun Zi Suan Jing. As its title implies, the book is divided into nine chapters. These nine chapters contain a total of 246 problems. The first eight of these chapters discuss calculation and problems that we would now solve using linear algebra. The last chapter is a study of right triangles and will be discussed below. First, we summarize the contents of some of the earlier parts.

The first chapter, whose title is “Rectangular Fields,” discusses how to express the areas of fields given their sides. Problem 1, for example, asks for the area of a rectangular field that is 15 bu by 16 bu.³ The answer, we see immediately, is 240 “square bu.” However, the Chinese original does not distinguish between linear and square units. The answer is given as “1 mu.” The Sun Zi Suan Jing explains that as a unit of length, 1 mu equals 240 bu. This ambiguity is puzzling, since a mu is both a length equal to 240 bu and the area of a rectangle whose dimensions are 1 bu by 240 bu. It would seem more natural for us if 1 mu of area were represented by a square of side 1 mu. If these units were described consistently, a square of side 1 linear mu would have an area equal to 240 “areal” mu. That there really is such a consistency appears in Problems 3 and 4, in which the sides are given in li. Since 1 li equals 300 bu (that is, 1.25 mu), to convert the area into mu one must multiply the lengths of the sides in li and then multiply by 1 . 25² · 240 = 375. Thus, one gets first “square mu” in the sense that we would understand it, and this numerical value for the area is then multiplied by the standard unit shape of 1 × 240 bu. The instructions say to multiply by precisely that number, and the answer is represented as a rectangle 1 bu by 375 bu.

Chapter 2 (“Millet and Rice”) of the Jiu Zhang Suan Shu contains problems very similar to the pesu problems from the Rhind papyrus. The proportions of millet and various kinds of rice and other grains are given as empirical data at the beginning of the chapter. Problems of the sort studied in this chapter occur frequently in all commercial transactions in all times. In the United States, for example, a concept analogous to pesu is the unit price (the number of dollars the merchant will obtain by selling 1 unit of the commodity in question). This number is frequently printed on the shelves of grocery stores to enable shoppers to compare the relative cost of purchasing different brands. Thus, the practicality of this kind of calculation is obvious. The 46 problems in Chapter 2, and also the 20 problems in Chapter 3 (“Proportional Distribution”) of the Jiu Zhang Suan Shu are of this type, including some extensions of the Rule of Three. For example, Problem 20 of Chapter 3 asks for the interest due on a loan of 750 qian repaid after 9 days if a loan of 1000 qian earns 30 qian interest each month (a month being 30 days). The result is obtained by forming the product 750 qian times 30 qian times 9 days and then dividing by the product 1000 qian times 30 days, yielding 6 qian. Here the product of the monthly interest on a loan of 1 qian and the number of days the loan is outstanding, divided by 30, forms the analog of the pesu for the loan; it is the number of qian of interest produced by each qian loaned.

Chapter 6 (“Fair Transportation”) is concerned with the very important problem of fair allocation of the burdens of citizenship. The Chinese idea of fairness, like that in many other places, including modern America, involves direct proportion. For example, Problem 1 considers a case of collecting taxes in a given location from four counties lying at different distances from the collection center and having different numbers of households. To solve this problem, a constant of proportionality is assigned to each county equal to the number of its households divided by its distance from the collection center. The amount of tax (in millet) each county is to provide is its constant divided by the sum of all the constants of proportionality and multiplied by the total amount of tax to be collected. The number of carts (of a total prescribed number) to be provided by each county is determined the same way. The data in the problem are as follows.

A total of 250,000 hu of millet were to be collected as tax, using 10,000 carts. The proportional parts for the four counties were therefore 10, 000 ÷ 8 = 1250, 9500 ÷ 10 = 950, 12, 350 ÷ 13 = 950, and 12, 200 ÷ 20 = 610, which the author reduced to 125, 95, 95, and 61. These numbers total 376. It therefore followed that county A should provide hu, that is, approximately 83,111.7 hu of millet and , or 3324 carts. The author rounded off the tax to three significant digits, giving it as 83,100 hu.

Along with these administrative problems, the 28 problems of Chapter 6 also contain some problems that have acquired an established place in algebra texts throughout the world and will be continue to be worked by students as long as there are teachers to require it. For example, Problem 26 considers a pond used for irrigation and fed by pipes from five different sources. Given that these five canals, each “working” alone, can fill the pond in , 1, , 3, and 5 days, the problem asks how long all five “working” together will require to fill it. The author realized that the secret is to add the rates at which the pipes “work” (the reciprocals of the times they require individually to fill the pond) and then take the reciprocal of this sum, and this instruction is given. The answer is 1/(3 + 1 + 2/5 + 1/3 + 1/5) = 15/74.

22.6 Early Chinese Geometry

Three early Chinese documents contain some geometry, always connected with the computation of areas and volumes. We shall discuss the geometry in them in chronological order.

22.6.1 The Zhou Bi Suan Jing

As mentioned above, the earliest Chinese mathematical document still in existence, the Zhou Bi Suan Jing, is concerned with astronomy and the applications of mathematics to the study of the heavens. The title refers to the use of the sundial or gnomon in astronomy. This is the physical model that led the Chinese to discover the Pythagorean theorem. Here is a paraphrase of the discussion:

Cut a rectangle whose width is 3 units and whose length is 4 (units) along its diagonal. After drawing a square on this diagonal, cover it with half-rectangles identical to the piece of the original rectangle that lies outside the square, so as to form a square of side 7. [See Fig. 22.2.] Then the four outer half-rectangles, each of width 3 and length 4, equal two of the original rectangles and hence have area 24. When this amount is subtracted from the square of area 49, the difference, which is the area of the square on the diagonal, is seen to be 25. The length of the diagonal is therefore 5.

Although the proof is given only for the easily computable case of the 3–4–5 right triangle, it is obvious that the geometric method is perfectly general, lacking only abstract symbols for unspecified numbers. In our terms, the author has proved that the length of the diagonal of a rectangle whose width is a and whose length is b is the square root of (a + b)² − 2ab. Note that this form of the theorem is not the “a² + b² = c²” that we are familiar with. The diagram is shown in Fig. 22.2 for the special case of a 3–4–5 triangle.

According to Li and Du (1987, p. 29), the vertical bar on a sundial was called gu in Chinese, and its shadow on the sundial was called gou; for that reason the Pythagorean theorem was known as the gougu theorem. Cullen (1996, p. 77) says that gu means thigh and gou means hook. All authorities agree that the hypotenuse was called xian (bowstring), which was also Aryabhata's name for it. The Zhou Bi Suan Jing says that the Emperor Yu was able to bring order into the realm because he knew how to use this theorem to compute distances. Zhao Shuang credited the Emperor Yu with saving his people from floods and other great calamities, saying that in order to do so he had to survey the shapes of mountains and rivers. Apparently the Emperor had drainage canals dug to channel floods out of the valleys and into the Yangtze and Yellow Rivers.

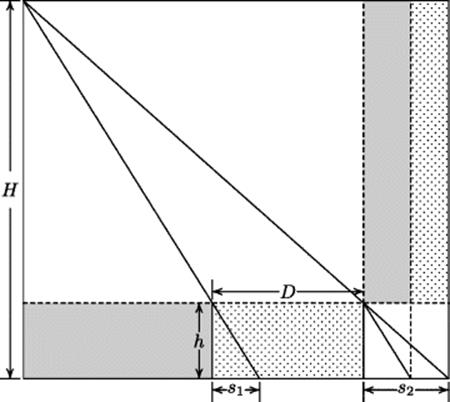
The third-century commentary on the Zhou Bi Suan Jing by Zhao Shuang explains a close variant of the method of surveying discussed in connection with the work of Aryabhata I in Chapter 20. The Chinese variant of the method is illustrated in Fig. 22.3, which assumes that the height H of an inaccessible object is to be determined. To determine H, it is necessary to put two poles of a known height h vertically into the ground in line with the object at a known distance D apart. The height h and the distance D are theoretically arbitrary, but the larger they are, the more accurate the results will be. After the poles are set up, the lengths of the shadows they would cast if the sun were at the inaccessible object are measured as s₁ and s₂. Thus the lengths s₁, s₂, h, and D are all known. A little trigonometry and algebra will show that

We have given the result as a formula, but as a set of instructions it is very easy to state in words: The required height is found by multiplying the height of the poles by the distance between them, dividing by the difference of the shadow lengths, and adding the height of the poles.

This method was expounded in more detail in a commentary on the Jiu Zhang Suan Shu written by Liu Hui in 263 CE. This commentary, along with the rest of the material on right triangles in the Jiu Zhang Suan Shu, eventually became a separate treatise, the Hai Dao Suan Jing (Sea Island Mathematical Manual; see Ang and Swetz, 1986). Liu Hui mentioned that this method of surveying could be found in the Zhou Bi Suan Jing and called it the double difference method (chong cha). The name apparently arises because the difference H − h is obtained by dividing Dh by the difference s₂ − s₁.

We have described the lengths s₁ and s₂ as shadow lengths here because that is the problem used by Zhao Shuang to illustrate the method of surveying. He attempts to calculate the height of the sun, given that at the summer solstice a stake 8 chi high casts a shadow 6 chi long and that the shadow length decreases by 1 fen for every 100 li that the stake is moved south, casting no shadow at all when moved 60,000 li to the south. This model assumes a flat earth, under which the shadow length is proportional to the distance from the pole to the foot of the perpendicular from the sun to the plane of the earth. Even granting this assumption, as we know, the sun is so distant from the earth that no lengthening or shortening of shadows would be observed. To any observable precision the sun's rays are parallel at all points on the earth's surface. The small change in shadow length that we observe is due to the curvature of the earth. But let us continue, accepting Zhao Shuang's assumptions.

To explain the solution of this problem, we first observe that two pieces of data are irrelevant to the problem. It does not matter how long a shadow is, since only the difference s₁ − s₂ occurs in the computational procedure. Likewise, the statement that the shadow disappears at a certain location (which, by the way, lies at an impossible distance away—the earth is not that big!) is irrelevant. The data here are D = 1000 li, s₂ − s₁ = 1 fen, h = 8 chi. One chiis about 25 centimeters, one fen is about 2.5 cm, and one li is 1800 chi, that is, about 450 meters. Our first job is to express everything in consistent units, say li. Thus, D = 1000, , and .

Because the pole height h is obviously insignificant in comparison with the height of the sun, we can neglect the first term in the formula we gave above, and we write

When we insert the appropriate values, we find, as did Zhao Shuang, that the sun is 80,000 li high, about 36,000 kilometers. Later Chinese commentators recognized that this figure was inaccurate, and in the eighth century an expedition to survey accurately a north–south line found the actual lengthening of the shadow to be 4 fen per thousand li. Notice that the statement of the problem seems to reveal careless editing over the years, since two methods of computing the height are implied here. If the two irrelevant pieces of information provided are taken into account, one can immediately use the similar triangles to infer the height of 80,000 li. This fact suggests that the original text was modified by later commentators, but that not all the parts that became irrelevant as a result of the modifications were removed.

Figure 22.2 Chinese illustration of the Pythagorean theorem.

Figure 22.3 The double-difference method of surveying.

22.6.2 The Jiu Zhang Suan Shu

The Jiu Zhang Suan Shu contains all the standard formulas for the areas of squares, rectangles, triangles, and trapezoids, along with the recognition of a relation between the circumference and the area of a circle, which we could interpret as a connection between the one-dimensional π and the two-dimensional π. The geometric formulas given in this treatise are more extensive than those of the Rhind papyrus; for example, there are approximate formulas for the volume of segment of a sphere and the area of a segment of a circle. It is perhaps not fair to compare the two documents, since the Rhind papyrus was written nearly two millennia earlier. The implied value of one-dimensional π, however, is π = 3. It is surprising to find this value so late, since it is known that the value 3.15147 had been obtained in China by the first century. According to Li and Du (1987, p. 68), Liu Hui refined it to 3.14 + 64/62500 = 3.141024 by approximating the area of a 192-sided polygon.⁴ That is, he started with a hexagon and doubled the number of sides five times.

Problems 31 and 32 ask for the area of a circular field of a given diameter and circumference.⁵ The method is to multiply half of the circumference by half of the diameter, which is exactly right in terms of Euclidean geometry; equivalently, the reader is told that one may multiply the two dimensions and divide by 4. In the actual data for problems, the diameter given is exactly one-third of the given circumference; in other words, the value assumed for one-dimensional π is 3. The assumption of that value leads to two other procedures for calculating the area: squaring the diameter, then multiplying by 3 and dividing by 4, or squaring the circumference and dividing by 12. An elaboration of this problem occurs in Problems 37 and 38, in which the area of an annulus (the region outside the smaller of two concentric circles and inside the larger) is given in terms of its width and the circumferences of the two circles.

The authors knew also how to find the volume of a pyramid. Problem 15 of Chapter 5 asks for the volume of a pyramid whose base is a rectangle 5 chi by 7 chi and whose height is 8 chi. The answer is given (correctly) as (cubic) chi. For a frustum of a pyramid having rectangular bases the recipe is to add twice the length of the upper base to the lower base and multiply by the width of the upper base to get one term. A second term is obtained symmetrically as twice the length of the lower base plus the length of the upper base, multiplied by the width of the lower base. These two terms are then added and multiplied by the altitude, after which one divides by 6. If the bases are a × b and c × d (the sides of length a and c being parallel) and the height is h, this yields what we would write (correctly) as

This result is more general than the rule given in the Moscow papyrus discussed in Section 7.2 of Chapter 7, which is given for a frustum with square bases.

The Pythagorean Theorem

The last of the nine chapters of the Jiu Zhang Suan Shu contains 24 problems on the gougu theorem. After a few “warm-up” problems in which two of the three sides of a right triangle are given and the third is to be computed, the problems become more complicated. Problem 11, for example, gives a rectangular door whose height exceeds its width by 6 chi, 8 cun and has a diagonal of 1 zhang. One zhang is 10 chi and 1 chi is 10 cun (apparently a variant rendering of fen). The recipe given is correct: Take half the difference of the height and width, square it, double, subtract from the square of the diagonal, then take the square root of half of the result. That process yields the average of the height and width, and given their semidifference of 3 chi, 4 cun, one can easily get both the width and the height.

22.6.3 The Sun Zi Suan Jing

The Sun Zi Suan Jing contains a few problems in measurement that are unusual enough to merit some discussion. An inverse area problem occurs in Problem 20, in which a circle is said to have area 35,000 square bu, and its circumference is required. Since the area is taken as one-twelfth of the square of the circumference, the author multiplies by 12, then takes the square root, getting bu.

Problems and Questions

Mathematical Problems

22.1 Compare the pond-filling problem (Problem 26 of Chapter 6) of the Jiu Zhang Suan Shu (discussed above) with the following problem from Greenleaf (1876, p. 125): A cistern has three pipes; the first will fill it in 10 hours, the second in 15 hours, and the third in 16 hours. What time will it take them all to fill it? Solve this problem. Is there any real difference between the two problems?

22.2 What happens to the estimate of the sun's altitude (36,000 km) given by Zhao Shuang if the “corrected” figure for shadow lengthening (4 fen per 1000 li) is used in place of the figure of 1 fen per 1000 li?

22.3 The gougu section of the Jiu Zhang Suan Shu contains the following problem: Under a tree 20 feet high and 3 in circumference there grows a vine, which winds seven times the stem of the tree and just reaches its top. How long is the vine?

Solve this problem. [Hint: Picture the tree as a cylinder. Imagine it has been cut down and rolled along the ground in the direction perpendicular to its axis in order to unwind the vine onto the ground. What would it the trace of the tree and the vine on the ground look like?]

Historical Questions

22.4 What uses were claimed for mathematics in the early Chinese classics?

22.5 What kinds of problems are studied in the nine chapters of the Jiu Zhang Suan Shu?

22.6 How is the Pythagorean theorem treated in the Zhou Bi Suan Jing?

Questions for Reflection

22.7 The fair taxation problem from the Jiu Zhang Suan Shu considered above treats distances and population with equal weight. That is, if the population of one county is double that of another, but that county is twice as far from the collection center, the two counties will have exactly the same tax assessment in grain and carts. Will this impose an equal burden on the taxpayers of the two counties? Is there a direct proportionality between distance and population that makes them interchangeable from the point of view of the taxpayers involved? Is the growing of extra grain to pay the tax fairly compensated by a shorter journey?

22.8 The Jiu Zhang Suan Shu implies that the diameter of a sphere is proportional to the cube root of its volume. Since this fact is equivalent to saying that the volume is proportional to the cube of the diameter, should we infer that the author knew both proportions? More generally, if an author knows (or has proved) “fact A,” and fact A implies fact B, is it accurate to say that the author knew or proved fact B?

22.9 How is the remainder problem of Sun Zi related to the kuttaka method of Brahmagupta. [Hint: The statement that x leaves a remainder of (say) 5 when divided by (say) 38 can be interpreted as saying there is an integer y such that x = 38y + 5. If you also want x to leave a remainder of (say) 4 when divided by (say) 15, you can write the equation x = 15z + 4. Eliminating x, you find 15z + 4 = 38y + 5, that is, 15z = 38y + 1. How do you find all solutions of this Diophantine equation?]

Notes

1. The Emperor was not hostile to learning, since he did not forbid the writing of books. Apparently, he just wanted to be remembered as the emperor in whose reign everything began.

2. Martzloff (1994) translates this title as Computational Prescriptions in Nine Chapters.

3. One bu is 600,000 hu, a hu being the diameter of a silk thread as it emerges from a silkworm. From other sources, it appears that 1 bu is about 1.5 meters.

4. Lam and Ang (1986) give the value as 3.14 + 169/625 = 3.142704.

5. All references to problem numbers and nomenclature in this section are based on the article of Lam (1994).