The history of mathematics: A brief course (2013)
Part IV. India, China, and Japan 500 BCE-1700 CE
Chapter 24. Traditional Japanese Mathematics
Japan adopted the Chinese system of writing, and along with it a huge amount of vocabulary. The establishment of Buddhism in Japan in the sixth century increased the rate of cultural importation from China and even from India. The courses of university instruction in mathematics in Japan were based on reading (in Chinese) the classics discussed in Chapter 22. In relation to Japan, the Koreans played a role as transmitters, passing on Chinese learning and inventions. This transmission process began in 553–554 when two Korean scholars, Wang Lian-tung and Wang Puson, journeyed to Japan. For many centuries both the Koreans and the Japanese worked within the system of Chinese mathematics. The earliest records of new and original work in these countries date from the seventeenth century. By that time, mathematical activity was exploding in Europe, and Europeans had begun their long voyages of exploration and colonization. There was only a comparatively brief window of time during which indigenous mathematics independent of Western influence could grow up in Japan.
In the following synopsis, Japanese names are given with the family name first. A word of explanation is needed about the names, however. Most Chinese symbols (kanji in Japanese) have at least two readings in Japanese. For example, the symbol read as CH![]() (middle) in the Japanese word for China (CH
(middle) in the Japanese word for China (CH![]() GOKU, the “Middle Kingdom”) is also read as naka in the surname Tanaka (“Middlefield”). These variant readings often cause trouble in names from the past, so that one cannot always be sure how a name was pronounced. As Mikami (p. viii) says, “We read Seki K
GOKU, the “Middle Kingdom”) is also read as naka in the surname Tanaka (“Middlefield”). These variant readings often cause trouble in names from the past, so that one cannot always be sure how a name was pronounced. As Mikami (p. viii) says, “We read Seki K![]() wa, although his personal name K
wa, although his personal name K![]() wa should have been read Takakazu.” One symbol in that name is now read as K
wa should have been read Takakazu.” One symbol in that name is now read as K![]() , but apparently was once also read as taka. These are the so-called ON (Chinese) and kun (Japanese) readings of the same symbol. The kun reading of this symbol does not seem to exist any longer; it means, incidentally, filial piety.1 A list of the names of some prominent mathematicians and their kanji rendering can be found at the end of the article by Martzloff (1990).
, but apparently was once also read as taka. These are the so-called ON (Chinese) and kun (Japanese) readings of the same symbol. The kun reading of this symbol does not seem to exist any longer; it means, incidentally, filial piety.1 A list of the names of some prominent mathematicians and their kanji rendering can be found at the end of the article by Martzloff (1990).
24.1 Chinese Influence and Calculating Devices
All the Japanese records now extant date from the time after Japan had adopted the Chinese writing system. Japanese mathematicians were for a time content to read the
Chinese classics. In 701 the emperor Monbu established a university system in which the mathematical part of the curriculum consisted of the Chinese Ten Classics. Some of these are no longer known, but the Zhou Bi Suan Jing, Sun Zi Suan Jing, Jiu Zhang Suan Shu, and Hai Dao Suan Jing, discussed in the two preceding chapters, were among them. Japan was disunited for many centuries after this early encounter with Chinese culture, and the mathematics that later grew up was the result of a reintroduction in the sixteenth and seventeenth centuries. Evidence of Chinese influence is seen in the mechanical methods of calculation used for centuries—counting rods, counting boards, and the abacus, which played an especially important role in Japan.
The abacus (suan pan) was invented in China, probably in the fourteenth century, when methods of computing with counting rods had become so efficient that the rods themselves were a hindrance to the performance of the computation. From China the invention passed to Korea, where it was known as the sanbob. Because it did not prove useful in Korean business, it did not become widespread there. It passed on to Japan, where it is known as the soroban. The Japanese made two technical improvements in the abacus: (1) They replaced the round beads by beads with sharp edges, which are easier to manipulate; and (2) they eliminated the superfluous second 5-bead on each string.
24.2 Japanese Mathematicians and Their Works
A nineteenth-century Japanese historian reported that in the late sixteenth century, the ruling lord Hideyoshi sent the scholar M![]() ri Shigeyoshi (dates unknown, also known as M
ri Shigeyoshi (dates unknown, also known as M![]() ri Kambei) to China to learn mathematics. According to the story, the Chinese ignored the emissary because he was not of noble birth. When he returned to Japan and reported this fact, Hideyoshi conferred noble status on him and sent him back. Unfortunately, his second visit to China coincided with Hideyoshi's unsuccessful attempt to invade Korea, which made his emissary unwelcome in China. M
ri Kambei) to China to learn mathematics. According to the story, the Chinese ignored the emissary because he was not of noble birth. When he returned to Japan and reported this fact, Hideyoshi conferred noble status on him and sent him back. Unfortunately, his second visit to China coincided with Hideyoshi's unsuccessful attempt to invade Korea, which made his emissary unwelcome in China. M![]() ri Shigeyoshi did not return to Japan until after the death of Hideyoshi. When he did return (in the early seventeenth century), he brought the abacus with him. Whether this story is true or not, it is a fact that M
ri Shigeyoshi did not return to Japan until after the death of Hideyoshi. When he did return (in the early seventeenth century), he brought the abacus with him. Whether this story is true or not, it is a fact that M![]() ri Shigeyoshi was one of the most influential early Japanese mathematicians. He wrote several treatises, all of which have been lost, but his work led to a great flowering of mathematical activity in seventeenth-century Japan through the work of his students. This mathematics was known as wasan, and written using Chinese characters. The word wasanis written with two Chinese characters. The first is WA, a character used to denote Japanese-style work in arts, crafts, and cuisine; it means literally harmony. The second is SAN, meaning calculation, the same Chinese symbol that represents suan in the many Chinese classics mentioned above.2 Murata (1994, p. 105) notes that the primary concern in wasan was to obtain elegant results, even when those results required very complicated calculations, and that “many Wasanists were men of fine arts rather than men of mathematics in the European sense.”
ri Shigeyoshi was one of the most influential early Japanese mathematicians. He wrote several treatises, all of which have been lost, but his work led to a great flowering of mathematical activity in seventeenth-century Japan through the work of his students. This mathematics was known as wasan, and written using Chinese characters. The word wasanis written with two Chinese characters. The first is WA, a character used to denote Japanese-style work in arts, crafts, and cuisine; it means literally harmony. The second is SAN, meaning calculation, the same Chinese symbol that represents suan in the many Chinese classics mentioned above.2 Murata (1994, p. 105) notes that the primary concern in wasan was to obtain elegant results, even when those results required very complicated calculations, and that “many Wasanists were men of fine arts rather than men of mathematics in the European sense.”
One unusual feature of mathematics during the Tokugawa Era from 1600 to 1868 was the choice of outlets in which to publish. Rather than writing letters to other scholars, or publishing in journals, as was common in Europe at this period, Japanese mathematicians would write books with problems in them to challenge other mathematicians. A phenomenon unique to Japanese mathematics is the tradition of sangaku (computational framed pictures), which were hung at Buddhist and Shint![]() shrines as votive plaques containing geometric problems leading to equations of higher degree. We shall discuss one of these in more detail below.
shrines as votive plaques containing geometric problems leading to equations of higher degree. We shall discuss one of these in more detail below.
According to Murata, the stimulus for the development of wasan came largely from two Chinese classics: the Suan Fa Tong Zong by Cheng Dawei, published in 1592, and the older treatise Suan Shu Chimeng (Introduction to Mathematical Studies) by Zhu Shijie (ca. 1260–ca. 1320), published in 1299. The latter was particularly important, since it came with no explanatory notes and a rebellion in China had made communication with Chinese scholars difficult. By the time this treatise was understood, the Japanese mathematicians had progressed beyond its contents.
24.2.1 Yoshida Koyu
M![]() ri Shigeyoshi trained three outstanding students during his lifetime, of whom we shall discuss only the first. This student was Yoshida Koyu (Yoshida Mitsuyoshi, 1598–1672). Being handicapped in his studies at first by his weakness in Chinese, Yoshida Koyu devoted extra effort to this language in order to read the Suan Fa Tong Zong. Having read this book, Yoshida Koyu made rapid progress in mathematics and soon excelled even M
ri Shigeyoshi trained three outstanding students during his lifetime, of whom we shall discuss only the first. This student was Yoshida Koyu (Yoshida Mitsuyoshi, 1598–1672). Being handicapped in his studies at first by his weakness in Chinese, Yoshida Koyu devoted extra effort to this language in order to read the Suan Fa Tong Zong. Having read this book, Yoshida Koyu made rapid progress in mathematics and soon excelled even M![]() ri Shigeyoshi himself. Eventually, he was called to the court of a nobleman as a tutor in mathematics. In 1627 Yoshida Koyu wrote a textbook in Japanese, the Jink
ri Shigeyoshi himself. Eventually, he was called to the court of a nobleman as a tutor in mathematics. In 1627 Yoshida Koyu wrote a textbook in Japanese, the Jink![]() -ki (Treatise on Large and Small Numbers), based on the Suan Fa Tong Zong. This work helped to popularize the abacus in Japan. It concluded with a list of challenge questions and thereby stimulated further work. These problems were solved in a later treatise, which, in turn, posed new mathematical problems to be solved; this was the beginning of a tradition of posing and solving problems that lasted for 150 years.
-ki (Treatise on Large and Small Numbers), based on the Suan Fa Tong Zong. This work helped to popularize the abacus in Japan. It concluded with a list of challenge questions and thereby stimulated further work. These problems were solved in a later treatise, which, in turn, posed new mathematical problems to be solved; this was the beginning of a tradition of posing and solving problems that lasted for 150 years.
24.2.2 Seki K![]() wa and Takebe Kenk
wa and Takebe Kenk![]()
One figure in seventeenth-century Japanese mathematics stands far above all others, a genius who is frequently compared with Archimedes, Newton, and Gauss.3 His name was Seki K![]() wa (Takakazu)—the wa is the same symbol found in wasan—and he was born around 1640, making him a contemporary of Newton and Leibniz. The stories told of him resemble stories told about other mathematical geniuses. For example, one of his biographers says that at the age of five, Seki K
wa (Takakazu)—the wa is the same symbol found in wasan—and he was born around 1640, making him a contemporary of Newton and Leibniz. The stories told of him resemble stories told about other mathematical geniuses. For example, one of his biographers says that at the age of five, Seki K![]() wa pointed out errors in a computation that was being discussed by his elders. A similar story is told about Gauss. Being the child of a samurai father and adopted by a noble family, Seki K
wa pointed out errors in a computation that was being discussed by his elders. A similar story is told about Gauss. Being the child of a samurai father and adopted by a noble family, Seki K![]() wa had access to books. He was mostly self-educated in mathematics, having paid little attention to those who tried to instruct him; in this respect he resembles Newton. Like Newton, he served as an advisor on high finance to the government, becoming examiner of accounts to the lord of Koshu. Unlike Newton, however, he was a popular teacher and physically vigorous. He became a shogunate samurai and master of ceremonies in the household of the Shogun. He died at the age of 66, leaving no direct heirs. His tomb in the Buddhist cemetery in Tokyo was rebuilt 80 years after his death by mathematicians of his school. His pedagogical activity earned him the title of Sansei, meaning Arithmetical Sage, a title that was carved on his tomb. Although he published very little during his lifetime, his work became known through his teaching activity, and he is said to have left copious notebooks.
wa had access to books. He was mostly self-educated in mathematics, having paid little attention to those who tried to instruct him; in this respect he resembles Newton. Like Newton, he served as an advisor on high finance to the government, becoming examiner of accounts to the lord of Koshu. Unlike Newton, however, he was a popular teacher and physically vigorous. He became a shogunate samurai and master of ceremonies in the household of the Shogun. He died at the age of 66, leaving no direct heirs. His tomb in the Buddhist cemetery in Tokyo was rebuilt 80 years after his death by mathematicians of his school. His pedagogical activity earned him the title of Sansei, meaning Arithmetical Sage, a title that was carved on his tomb. Although he published very little during his lifetime, his work became known through his teaching activity, and he is said to have left copious notebooks.
Seki K![]() wa made profound contributions to several areas of mathematics, in some cases anticipating results that were being obtained independently in Europe about this time. According to Mikami (p. 160), he kept his technique a secret from the world at large, but apparently he confided it to his pupil Takebe Kenk
wa made profound contributions to several areas of mathematics, in some cases anticipating results that were being obtained independently in Europe about this time. According to Mikami (p. 160), he kept his technique a secret from the world at large, but apparently he confided it to his pupil Takebe Kenk![]() (Takebe Katahiro, 1664–1739). Some scholars say that Takebe Kenk
(Takebe Katahiro, 1664–1739). Some scholars say that Takebe Kenk![]() refused to divulge the secret, saying, “I fear that one whose knowledge is so limited as mine would tend to misrepresent its significance.” However, other scholars claim that Takebe Kenk
refused to divulge the secret, saying, “I fear that one whose knowledge is so limited as mine would tend to misrepresent its significance.” However, other scholars claim that Takebe Kenk![]() did write an exposition of the latter method and that it amounts to the principles of cancelation and transposition. These two scholars, together with Takebe Kenk
did write an exposition of the latter method and that it amounts to the principles of cancelation and transposition. These two scholars, together with Takebe Kenk![]() 's brother, compiled a 20-volume encyclopedia, the Taisei Sanky
's brother, compiled a 20-volume encyclopedia, the Taisei Sanky![]() (Great Mathematical Treatise), containing all the mathematics known in their day.
(Great Mathematical Treatise), containing all the mathematics known in their day.
Takebe Kenk![]() also wrote a book that is unique in its time and place, bearing the title Tetsujutsu Sanky
also wrote a book that is unique in its time and place, bearing the title Tetsujutsu Sanky![]() (roughly, The Art of Doing Mathematics, published in 1722), in which he speculated on the metaphysics of mathematical concepts and the kind of psychology needed to solve different types of mathematical problems (Murata, 1994, pp. 107–108).
(roughly, The Art of Doing Mathematics, published in 1722), in which he speculated on the metaphysics of mathematical concepts and the kind of psychology needed to solve different types of mathematical problems (Murata, 1994, pp. 107–108).
In Japan, knowledge of the achievements of Western mathematicians became widespread in the late nineteenth century, while the flow of knowledge in the opposite direction has taken longer. A book entitled The Theory of Determinants in the Historical Order of Development, which is a catalog of papers on the subject with commentaries, was published by the South African mathematician Thomas Muir (1844–1934) in 1905. Although this book consists of four volumes totaling some 2000 pages, it does not mention Seki K![]() wa, the true discoverer of determinants!
wa, the true discoverer of determinants!
24.2.3 The Modern Era in Japan
In the seventeenth century, the Tokugawa shoguns adopted a policy of exclusion vis-à-vis the West, one that could be enforced in an island kingdom such as Japan. Commercial contacts with the Dutch, however, resulted in some cultural penetration, and Western mathematical advances came to be known little by little in Japan. By the time Japan was opened to the West in the mid-nineteenth century, Japanese mathematicians were already aware of many European topics of investigation. In joining the community of nations for trade and politics, Japan also joined it intellectually. In the early nineteenth century, Japanese mathematicians were writing about such questions as the rectification of the ellipse, a subject of interest in Europe at the same period. By the end of the nineteenth century, there were several Japanese mathematical journals publishing (in European languages) mathematical work comparable to what was being done in Europe at the same period, and a few European scholars were already reading these journals to see what advances were being made by the Japanese. In the twentieth century the number of Japanese works being read in the West multiplied, and Japanese mathematicians such as Gor![]() Shimura (b. 1930), Sh
Shimura (b. 1930), Sh![]() shichi Kobayashi (b. 1932), and many others have been among the leaders in nearly every field of mathematics.
shichi Kobayashi (b. 1932), and many others have been among the leaders in nearly every field of mathematics.
24.3 Japanese Geometry and Algebra
During the seventeenth and eighteenth centuries there was a tradition of geometric challenge problems in Japan. The geometric problems usually involved combinations of simple figures whose areas or volumes were known but which were arranged in such a way that finding their parts became an intricate problem in algebra. The word algebra needs to be emphasized here. The challenge in these problems was only superficially geometric; it was largely algebraic. The challenge was much greater to the Japanese mathematicians of the time than it is to us, since they did not have what we know as trigonometry. (They did have a rudimentary trigonometry, but they solved most problems using just the Pythagorean theorem.) We begin our discussion of this era by mentioning a few of the challenge problems. Afterward, we shall briefly discuss the infinitesimal methods used to solve the problems of measuring arcs, areas, and volumes in spheres.
One impetus to the development of mathematics in Japan came with the arrival of the Chinese “celestial element method” (tian yuan shu). This name was given to the unknown in an equation by Li Ye (1192–1279, also known as Li Zhi) in his 1248 treatise Ceyuan Haijing (Sea Mirror of Circle Measurements, see Mikami, 1913, p. 81).4 This term passed to Korea as ch'onwonsul and thence to Japan as tengen jutsu, which also means “celestial element method.” This Chinese algebra became part of the standard Japanese curriculum before the seventeenth century.
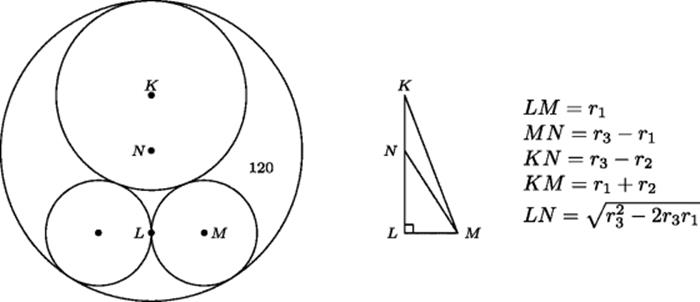
Fifteen problems were published by Sawaguchi Kazuyuki (dates unknown) in his 1670 work Kokon Samp![]() -ki (Ancient and Modern Mathematics). As an example of the complexity of these problems, consider the first of them. In this problem there are three circles, each externally tangent to the other two and internally tangent to a fourth circle, as in Fig. 24.1. The diameters of two of the enclosed circles are equal and the third enclosed circle has a diameter five units larger. The area inside the enclosing circle and outside the three smaller circles is 120 square units. The problem is to compute the diameters of all four circles. Without a computer algebra system, most people, even nowadays, would not wish to attempt to solve this problem. As Fig. 24.1 shows, the problem leads to the simultaneous equations
-ki (Ancient and Modern Mathematics). As an example of the complexity of these problems, consider the first of them. In this problem there are three circles, each externally tangent to the other two and internally tangent to a fourth circle, as in Fig. 24.1. The diameters of two of the enclosed circles are equal and the third enclosed circle has a diameter five units larger. The area inside the enclosing circle and outside the three smaller circles is 120 square units. The problem is to compute the diameters of all four circles. Without a computer algebra system, most people, even nowadays, would not wish to attempt to solve this problem. As Fig. 24.1 shows, the problem leads to the simultaneous equations
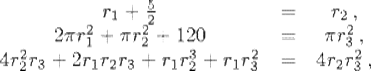
where r1, r2, and r3 are the radii of the circles. The last of these relations results from applying the Pythagorean theorem first to the triangle LMN to get LM and then to KLM.
Figure 24.1 Sawaguchi Kazuyuki's first problem.
This problem was solved by Seki K![]() wa (Smith and Mikami, 1914, pp. 96–97). In case Seki K
wa (Smith and Mikami, 1914, pp. 96–97). In case Seki K![]() wa's prowess in setting up and solving equations was not clear from his solution of this problem, we note that he also solved the fourteenth of these problems, the “quadrilateral problem” (see below), which allegedly led to an equation of degree 1458. Although the procedure was a mechanical one, using counting boards, prodigious concentration must have been required to execute it. What a chess player Seki K
wa's prowess in setting up and solving equations was not clear from his solution of this problem, we note that he also solved the fourteenth of these problems, the “quadrilateral problem” (see below), which allegedly led to an equation of degree 1458. Although the procedure was a mechanical one, using counting boards, prodigious concentration must have been required to execute it. What a chess player Seki K![]() wa could have been! As Mikami (1913, p. 160) remarks, “Perseverance and hard study were a part of the spirit that characterized Japanese mathematics of the old times.”
wa could have been! As Mikami (1913, p. 160) remarks, “Perseverance and hard study were a part of the spirit that characterized Japanese mathematics of the old times.”
24.3.1 Determinants
Seki K![]() wa is given the credit for inventing one of the central ideas of modern mathematics: determinants. He introduced this subject in 1683 in Kai Fukudai no H
wa is given the credit for inventing one of the central ideas of modern mathematics: determinants. He introduced this subject in 1683 in Kai Fukudai no H![]() (Method of Solving Fukudai Problems).5 Nowadays, determinants are usually introduced in connection with linear equations, but Seki K
(Method of Solving Fukudai Problems).5 Nowadays, determinants are usually introduced in connection with linear equations, but Seki K![]() wa developed them in relation to equations of higher degree as well. The method is explained as follows.
wa developed them in relation to equations of higher degree as well. The method is explained as follows.
Suppose that we are trying to solve two simultaneous quadratic equations
![]()
When we eliminate x2, we find the linear equation
![]()
Similarly, if we eliminate the constant term from the original equations and then divide by x, we find
![]()
Thus from two quadratic equations we have derived two linear equations. Seki K![]() wa called this process tatamu (folding).
wa called this process tatamu (folding).
We have written out expressions for the simple 2 × 2 determinants here. For example,
![]()
but, as everyone knows, the full expanded expressions for determinants are cumbersome even for the 3 × 3 case. It is therefore important to know ways of simplifying such determinants, using the structural properties we now call the multilinear property and the alternating property. Seki K![]() wa knew how to make use of the multilinear property to take out a common factor from a given row. He not only formulated the concept of a determinant but also knew many of their properties, including how to determine which terms are positive and which are negative in the expansion of a determinant. It is interesting that determinants were introduced in Europe around the same time (1693, by Leibniz), but in a comparatively limited context.6 As Smith and Mikami (1914, p. 125) say,
wa knew how to make use of the multilinear property to take out a common factor from a given row. He not only formulated the concept of a determinant but also knew many of their properties, including how to determine which terms are positive and which are negative in the expansion of a determinant. It is interesting that determinants were introduced in Europe around the same time (1693, by Leibniz), but in a comparatively limited context.6 As Smith and Mikami (1914, p. 125) say,
It is evident that Seki was not only the discoverer but that he had a much broader idea than that of his great German contemporary.
Determinants are not the only topic on which Seki was on a par with the European mathematicians of his time. In one of his works, the Katsuy![]() Samp
Samp![]() (Compendium of the Major Computational Rules) published posthumously in 1712 (the year before the publication of James Bernoulli's Ars conjectandi), Seki gave a table of what are now called Bernoulli numbers. (See Smith and Mikami, 1914, p. 108.)
(Compendium of the Major Computational Rules) published posthumously in 1712 (the year before the publication of James Bernoulli's Ars conjectandi), Seki gave a table of what are now called Bernoulli numbers. (See Smith and Mikami, 1914, p. 108.)
24.3.2 The Challenge Problems
As mentioned above, in 1627 Yoshida Koyu (1598–1672) wrote the Jink![]() -ki, concluding it with a list of challenge questions. Here are some of those questions:
-ki, concluding it with a list of challenge questions. Here are some of those questions:
1. There is a log of precious wood 18 feet long whose bases are 5 feet and ![]() feet in circumference. Into what lengths should it be cut to trisect the volume?
feet in circumference. Into what lengths should it be cut to trisect the volume?
2. There have been excavated 560 measures of earth, which are to be used for the base of a building. The base is to be 3 measures square and the building is to be 9 measures high. Required, the size of the upper base.
3. There is a mound of earth in the shape of a frustum of a circular cone. The circumferences of the bases are 40 measures and 120 measures and the mound is 6 measures high. If 1200 measures of earth are taken evenly off the top, what will be the height?
4. A circular piece of land 100 [linear] measures in diameter is to be divided among three persons so that they shall receive 2900, 2500, and 2500 [square] measures, respectively. Required, the lengths of the chords and the altitudes of the segments.
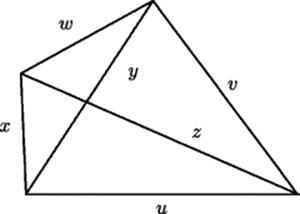
Seki K![]() wa solved a geometric problem that would challenge even the best algebraist today. It was the fourteenth in a list of challenge problems posed by Sawaguchi Kazuyuki: There is a quadrilateral whose sides and diagonals are u,
wa solved a geometric problem that would challenge even the best algebraist today. It was the fourteenth in a list of challenge problems posed by Sawaguchi Kazuyuki: There is a quadrilateral whose sides and diagonals are u, ![]() ,
, ![]() , x, y, and z [as shown in Fig. 24.2].
, x, y, and z [as shown in Fig. 24.2].
Figure 24.2 Sawaguchi Kazuyuki's quadrilateral problem.
It is given that
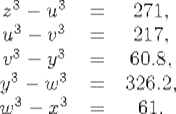
Required, to find the values of u, ![]() ,
, ![]() , x, y, z.
, x, y, z.
The fact that the six quantities are the sides and diagonals of a quadrilateral provides one equation that they must satisfy, namely:
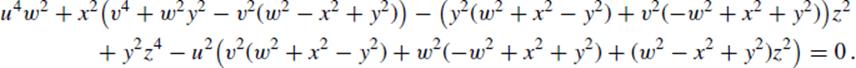
This equation, together with the five given conditions, provides a complete set of equations for the six quantities. However, Seki K![]() wa's explanation, which is only a sketch, does not mention this sixth equation, so it may be that what he solved was the indeterminate problem given by the other five equations. That, however, would be rather strange, since then the quadrilateral would play no role whatsoever in the problem. Whatever the case, it is known that such equations were solved numerically by the Chinese using a counting board.
wa's explanation, which is only a sketch, does not mention this sixth equation, so it may be that what he solved was the indeterminate problem given by the other five equations. That, however, would be rather strange, since then the quadrilateral would play no role whatsoever in the problem. Whatever the case, it is known that such equations were solved numerically by the Chinese using a counting board.
The quadrilateral problem of Sawaguchi Kazuyuki led to an equation of degree 1458, solved by Seki K![]() wa (who was Sawaguchi Kazuyuki's teacher). Again we emphasize that this problem—like many of the problems in the sangaku plaques and like many problems studied by mathematicians from Mesopotamia to India—seems to be inspired by the desire to do some complicated algebra rather than by any pressing geometric need.
wa (who was Sawaguchi Kazuyuki's teacher). Again we emphasize that this problem—like many of the problems in the sangaku plaques and like many problems studied by mathematicians from Mesopotamia to India—seems to be inspired by the desire to do some complicated algebra rather than by any pressing geometric need.
24.3.3 Beginnings of the Calculus in Japan
By the end of the seventeenth century the wasanists were beginning to use techniques that resemble the infinitesimal methods being used in Europe about this time. Of course, in one sense Zu Chongzhi had used some principles of calculus 1000 years earlier in his application of Cavalieri's principle to find the volume of a sphere. The intuitive basis of the principle is that equals added to equals yield equal sums, and a solid can be thought of as the sum of its horizontal sections. It isn't really, of course. No finite sum of areas and no limit of such a sum can ever have positive volume. Students in calculus courses learn to compute volumes using approximating sums that are very thin prisms, but not infinitely thin.
In Japan these techniques were first applied in the area called yenri (circle theory),7 a topic that had been studied extensively in China. The idea of approximating by shells or disks, now a basic part of courses in calculus, can be seen in the 1684 edition of the Ketsugi-sh![]() (Combination Book), first published in 1660 by Isomura Kittoku (dates unknown).
(Combination Book), first published in 1660 by Isomura Kittoku (dates unknown).
Isomura Kittoku's computation of the volume of a sphere. Copyright © Stock Montage.
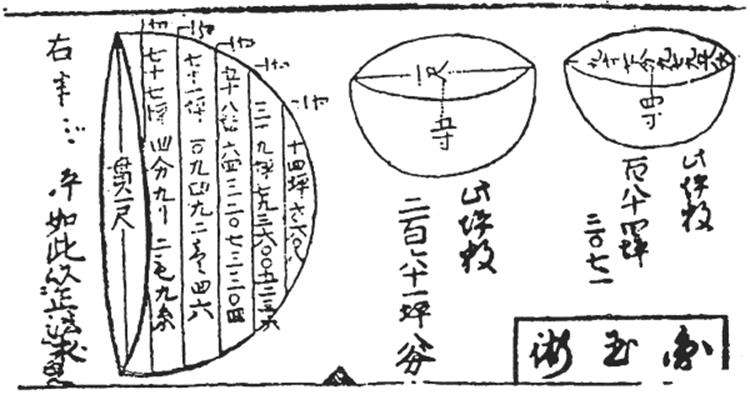
Isomura Kittoku explained the method as follows (Mikami, 1913, p. 204):
If we cut a sphere of diameter 1 foot into 10,000 slices, the thickness of each slice is 0.0001 feet, which will be something like that of a very thin paper. Finding in this way the volume of each of them, we sum up the results, 10,000 in number, when we get 523.6 measures [that is, a volume of 0.5236 cubic feet]. Besides, it is true, there are small incommensurable parts, which are neglected.
Since the volume of this sphere is π/6 ≈ 0.5235987756, this technique is quite accurate. All that is required to get it is the formula for the area of a circle, plus the Pythagorean theorem to determine the square of the radius of each slice. Except for the numerical value of π, all this can be done in integer arithmetic, with no error, provided the radius is an integer. The technique of obtaining extraordinary precision and using it to perform numerical experiments that provide the basis for inductive reasoning is very close to the technique used by Bhaskara II (see Chapter 21) to compute the surface area of a sphere. It also appears in a remarkable infinite series attributed to Takebe Kenk![]() , as we shall now see.
, as we shall now see.
Takebe Kenk![]() 's method of rectifying the circle was based on a relation, which he apparently discovered in 1722, between the square of half of an arc, the height h of the arc,8 and the diameter d of the circle. Here is his own description of this discovery, as explained by Smith and Mikami (pp. 1914, 147–149). He began with height h = 0.000001 = 10−6 and d = 10, finding the square of the arc geometrically with accuracy to 53 decimal places. The value of the square of this arc is
's method of rectifying the circle was based on a relation, which he apparently discovered in 1722, between the square of half of an arc, the height h of the arc,8 and the diameter d of the circle. Here is his own description of this discovery, as explained by Smith and Mikami (pp. 1914, 147–149). He began with height h = 0.000001 = 10−6 and d = 10, finding the square of the arc geometrically with accuracy to 53 decimal places. The value of the square of this arc is
![]()
According to Smith and Mikami (1914, p. 148), the value given by Takebe Kenk![]() was
was
![]()
But this value does not fit with the procedure followed by Takebe Kenk![]() ; it does not even yield the correct first approximation. The figure given by Smith and Mikami appears to represent the value obtained by Takebe Kenk
; it does not even yield the correct first approximation. The figure given by Smith and Mikami appears to represent the value obtained by Takebe Kenk![]() afterthe first approximation was subtracted, but with the result multiplied by the square of the diameter.9 In appreciating Takebe Kenk
afterthe first approximation was subtracted, but with the result multiplied by the square of the diameter.9 In appreciating Takebe Kenk![]() 's method, the first problem to be solved is the source of this extremely accurate measurement of the circle. According to Smith and Mikami (1914, p. 148), Takebe Kenk
's method, the first problem to be solved is the source of this extremely accurate measurement of the circle. According to Smith and Mikami (1914, p. 148), Takebe Kenk![]() said that the computation was given in two other works, both of which are now lost.
said that the computation was given in two other works, both of which are now lost.
The first clue that strikes us in this connection is the seemingly strange choice of the square of the arc rather than the arc itself. Why would it be easier to compute the square of the arc than the arc itself? An answer readily comes to mind: Half of the arc is approximated by its chord, and the chord is one side of a convenient right triangle. In fact, the chord of half of an arc is the mean proportional between the diameter of the circle and the height of the full arc, so that in this case it is ![]() . When we square it, we get just dh = 10−5, which acts as Takebe Kenk
. When we square it, we get just dh = 10−5, which acts as Takebe Kenk![]() 's first approximation. That result suggests that the length of the arc was reached by repeatedly bisecting the arc, taking the chord as an approximation. This hypothesis gains plausibility, since it is known that this technique had been used earlier to approximate π. Since a2 = 4(a/2)2, it was only necessary to find the square of half the arc, then multiply by 4. The ratio of the chord to the diameter is even easier to handle, especially since Takebe Kenk
's first approximation. That result suggests that the length of the arc was reached by repeatedly bisecting the arc, taking the chord as an approximation. This hypothesis gains plausibility, since it is known that this technique had been used earlier to approximate π. Since a2 = 4(a/2)2, it was only necessary to find the square of half the arc, then multiply by 4. The ratio of the chord to the diameter is even easier to handle, especially since Takebe Kenk![]() has taken the diameter to be 10. If x is the square of this ratio for a given chord, the square of ratio for the chord of half of the arc is
has taken the diameter to be 10. If x is the square of this ratio for a given chord, the square of ratio for the chord of half of the arc is ![]() . In other words, the iterative process
. In other words, the iterative process ![]() makes the bisection easy. If we were dealing with the arc instead of its square, each step in that process would involve two square roots instead of one. Even as it is, Takebe Kenk
makes the bisection easy. If we were dealing with the arc instead of its square, each step in that process would involve two square roots instead of one. Even as it is, Takebe Kenk![]() must have been a calculating genius to iterate this process enough times to get 53 decimal places of accuracy without making any errors. The result of 50 applications yields a ratio which, multiplied by 100 · 450, is
must have been a calculating genius to iterate this process enough times to get 53 decimal places of accuracy without making any errors. The result of 50 applications yields a ratio which, multiplied by 100 · 450, is
![]()
This number of iterations gives 38 decimal places of accuracy. Even with this plausible method of procedure, it still strains credibility that Takebe Kenk![]() achieved the claimed precision. However, let us pass on to the rest of his method.
achieved the claimed precision. However, let us pass on to the rest of his method.
After the first approximation hd is subtracted, the new error is 10−12 times 0.3333333 . . . , which suggests that the next correction should be 10−12/3. But this is exactly h2/3, in other words h/(3d) times the first term. When it is subtracted from the previously corrected value, the new error is
![]()
The long string of 7's here suggests that this number is 10−19 times ![]() , which is (8h)/(15d) times the previous correction. By continuing for a few more terms, Takebe Kenk
, which is (8h)/(15d) times the previous correction. By continuing for a few more terms, Takebe Kenk![]() was able to observe a pattern: The corrections are obtained by multiplying successively by h/(3d), (8h)/(15d), (9h)/(14d), (32h)/(45d), (25h)/(33d), . . . . Some sensitivity to the factorization of integers is necessary to see the recursive operation: multiplication by (h/d)[2n2/(n + 1)(2n + 1)]. Putting these corrections together as an infinite series leads to the expression
was able to observe a pattern: The corrections are obtained by multiplying successively by h/(3d), (8h)/(15d), (9h)/(14d), (32h)/(45d), (25h)/(33d), . . . . Some sensitivity to the factorization of integers is necessary to see the recursive operation: multiplication by (h/d)[2n2/(n + 1)(2n + 1)]. Putting these corrections together as an infinite series leads to the expression
![]()
when the full arc has length a.
In using this numerical approach, Takebe Kenk![]() had reached his conclusion inductively. This induction was based on a faith (which turns out to be justified) that the successive approximations are rational numbers that satisfy a fairly simple recursive formula. As you probably know, the power series for the sine, cosine, exponential, and logarithm have this happy property, but the series for the tangent, for example, does not.
had reached his conclusion inductively. This induction was based on a faith (which turns out to be justified) that the successive approximations are rational numbers that satisfy a fairly simple recursive formula. As you probably know, the power series for the sine, cosine, exponential, and logarithm have this happy property, but the series for the tangent, for example, does not.
This series solves the problem of rectification of the circle and hence all problems that depend on knowing the value of π. In modern terms the series given by Takebe Kenk![]() represents the function
represents the function
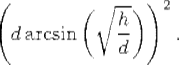
Takebe Kenk![]() 's discovery of this result in 1722 falls between the discovery of the power series for the arcsine function by Newton in 1676 and its publication by Euler in 1737. For an arc of 60°, we have d = 2r and
's discovery of this result in 1722 falls between the discovery of the power series for the arcsine function by Newton in 1676 and its publication by Euler in 1737. For an arc of 60°, we have d = 2r and ![]() ; and with these values, ten terms of the series will approximate π2/36 to 15 decimal places (when r = 1).
; and with these values, ten terms of the series will approximate π2/36 to 15 decimal places (when r = 1).
24.4 Sangaku
The shoguns of the Tokugawa Era (1600–1868) concentrated their foreign policy on relations with China and held Western visitors at arms length, with the result that Japan was nearly closed to the Western world for 250 years. During this time a form of mathematics known as sangaku (literally, framed computations) arose. As mentioned above, the sangaku were votive tablets containing mathematical problems posted at Buddhist and Shint![]() shrines as a challenge to others and an expression of piety. A comprehensive exhibition of sangaku from many parts of Japan was organized in 2005 at the Nagoya Museum of Science, and a book with full color illustrations from that exhibit was published. (See Fukagawa, 2005.)
shrines as a challenge to others and an expression of piety. A comprehensive exhibition of sangaku from many parts of Japan was organized in 2005 at the Nagoya Museum of Science, and a book with full color illustrations from that exhibit was published. (See Fukagawa, 2005.)
In 1806, Ehara Masanori (dates unknown) hung a colorful picture of the diagram sketched in Fig. 24.3 at the Atsuta Shint![]() shrine in Owari Province10 It was subsequently lost, but not before the Owari scholar Kitagawa M
shrine in Owari Province10 It was subsequently lost, but not before the Owari scholar Kitagawa M![]() ko (1763–1839) made a pilgrimage to the shrine and solved the problem. From his description of the problem and his solution, the people at the shrine were able to reconstruct the replica of the original document shown in Fig. 24.4.
ko (1763–1839) made a pilgrimage to the shrine and solved the problem. From his description of the problem and his solution, the people at the shrine were able to reconstruct the replica of the original document shown in Fig. 24.4.
Figure 24.3 A sangaku problem.
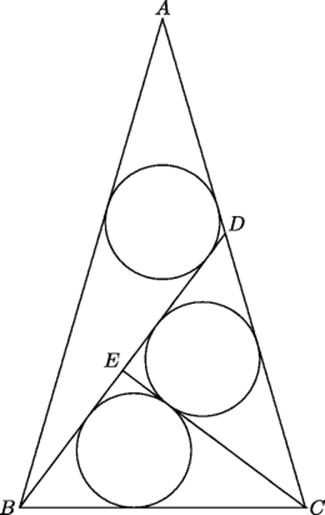
Figure 24.4 A disk cut into sectors and opened up.
Here is the problem as reconstructed:In Fig. 24.3, the triangle ABC is isosceles. The line BD has been drawn meeting the bisector CE of ∠C at right angles. Obviously then, CD = BC, and the triangles CDE and CBE are congruent. Therefore their inscribed circles are also congruent. The remarkable thing about this particular triangle is that the circle inscribed in triangle BDA is also congruent to the other two circles. The problem asks for the common radius of the three circles (in terms of the line CE).
This problem is discussed in the book by Fukagawa and Rothman (2008). The problem is stated on pages 194–196, and the solution by Kitagawa M![]() ko is given on pages 212–216.
ko is given on pages 212–216.
24.4.1 Analysis
It should be observed first of all that there is precisely one base angle for the isosceles triangle such that these three circles are all the same size, and it is somewhere between 60° and 90°. The third circle degenerates to a point when the base angles are ![]() (the triangle is equilateral), while the radius of the other two circles is
(the triangle is equilateral), while the radius of the other two circles is ![]() . On the other hand, when the base angles become
. On the other hand, when the base angles become ![]() (the triangle degenerates to an infinite strip), the radius of the upper circle is
(the triangle degenerates to an infinite strip), the radius of the upper circle is ![]() while that of the two lower triangles is
while that of the two lower triangles is ![]() . Thus, the upper circle grows to be bigger than the two lower circles as the base angles increase. Hence, there is precisely one angle for which this condition can be met (and it is between 73° and 74°).
. Thus, the upper circle grows to be bigger than the two lower circles as the base angles increase. Hence, there is precisely one angle for which this condition can be met (and it is between 73° and 74°).
Problems and Questions
Mathematical Problems
24.1 Given the very broad hint that z = 10, u = 9, ![]() ,
, ![]() , and x = 4, solve the quadrilateral problem to get an exact expression for y, and exact expressions for which the data of the problem (the numbers 60.8 and 326.2) are approximations.
, and x = 4, solve the quadrilateral problem to get an exact expression for y, and exact expressions for which the data of the problem (the numbers 60.8 and 326.2) are approximations.
24.2 Early on, Japanese mathematicians believed the area of the sphere to be one-fourth the square of the circumference, that is, π2r2 rather than the true value 4πr2. This value was stated in the first (1660) edition of Isomura Kittoku's Ketsugi-Sho and corrected in a later edition. Smith and Mikami (1914, p. 75) suggest a way in which this belief might have appeared plausible. To explain it, we first need to see an example in which the same line of reasoning really does work.
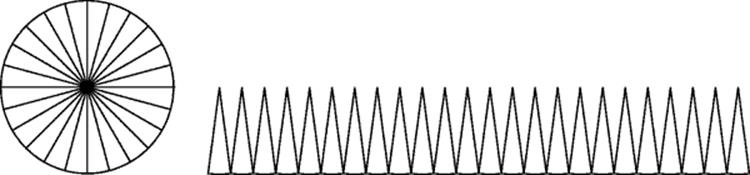
By imagining a circle sliced like a pie into a very large number of very thin pieces, one can imagine it cut open and all the pieces laid out next to one another, as shown in Fig. 24.4. Because these pieces are very thin, their bases are such small arcs of the circle that each base resembles a straight line. Neglecting a very tiny error, we can say that if there are n pieces, the base of each piece is a straight line of length 2πr/n. The sectors are then essentially triangles of height r (because of their thinness) and hence area (1/2) · (2πr2)/n. Since there are n of them, the total area is πr2. This heuristic argument (exactly what Archimedes stated in the letter accompanying his paper on the surface of the sphere) gives the correct result. In fact, this very figure appears in a Japanese work from 1698 (Smith and Mikami, 1914 p. 131).
Now imagine a hemispherical bowl covering the pie. If the slices are extended upward so as to slice the bowl into equally thin segments, and those sectors are then straightened out and arranged like the sectors of the pie, they also will have bases equal to ![]() , but their height will be one-fourth of the circumference, in other words, πr/2, giving a total area for the hemisphere of (1/2) · π2r2. Since the area is 2πr2, this would imply that π = 4. How much error would there be in taking π = 4?
, but their height will be one-fourth of the circumference, in other words, πr/2, giving a total area for the hemisphere of (1/2) · π2r2. Since the area is 2πr2, this would imply that π = 4. How much error would there be in taking π = 4?
24.3 Problem 41 of Isomura Kittoku (Smith and Mikami, 1914, p. 68) is given as the following: There is a log 18 feet long, whose ends have diameters 1 foot and 2.6 feet. It is wound spirally with 75 feet of string, the coils being 2.5 feet apart. How many coils are there?
This problem seems to be overdetermined, since the length of the log and the distance between the coils would already determine the number of coils. The maximum number would be 7.2, but the total length of them would be only a little over 40 feet. Omitting the assumption that the coils are 2.5 feet apart, solve the problem that remains.
Historical Questions
24.4 When and how did mathematical research arise in Japan, and how did mathematicians learn their subject?
24.5 What areas of mathematics became specialties in Japan, and what innovations arose there?
24.6 What is sangaku?
Questions for Reflection
24.7 What is wrong with the reasoning above that leads to the conclusion that the area of a sphere is one-fourth the square of the circumference?
24.8 What is the justification for the statement by the historian of mathematics T. Murata that Japanese mathematics (wasan) was not a science but an art?
24.9 Why might Seki K![]() wa and other Japanese mathematicians have wanted to keep their methods secret, and why did their students, such as Takebe Kenk
wa and other Japanese mathematicians have wanted to keep their methods secret, and why did their students, such as Takebe Kenk![]() , honor that wish?
, honor that wish?
Notes
1. When Japanese words are rendered in the Latin alphabet, it is customary to capitalize the ON pronunciations and write the kun in lowercase. The words wasan and sangaku that we shall be introducing are both ON readings, but we shall omit the capitalization.
2. The modern Japanese word for mathematics is S![]() GAKU, meaning literally number theory.
GAKU, meaning literally number theory.
3. His biography suggests that the real comparison should be with Pythagoras, since he assembled a devoted following, and his followers were inclined to attribute results to him even when his direct influence could not be established. Newton and Gauss were not “people persons,” and Gauss hated teaching. But Seki K![]() wa had a close relationship with his students.
wa had a close relationship with his students.
4. According to Libbrecht (1973, pp. 345–346), the same word had been used in a rather different and obscure sense by Qin Jiushao a year earlier in his Shu Shu Jiu Zhang.
5. The word fukudai seems to be related to fukugen suru, meaning reconstruct or restore. According to Smith and Mikami (1914, p. 124), Seki K![]() wa's school offered five levels of diploma, the third of which was called the fukudai menkyo (fukudai license) because it involved knowledge of determinants.
wa's school offered five levels of diploma, the third of which was called the fukudai menkyo (fukudai license) because it involved knowledge of determinants.
6. A recent paper whose author has not yet given permission for citation gives strong evidence that much of matrix theory as we now know it was common throughout Eurasia during the Medieval period, and that in fact the West may actually have learned about determinants from China.
7. The symbol for circle (yen) is also the symbol for the Japanese unit of currency; in Japan, it is actually pronounced “en.”
8. This height is called the sagitta (arrow) by lens grinders, a name first bestowed on it in India. It is now called the versed sine in mathematics. In our terms, it is 1 − cos θ times the radius.
9. Even so, there is one 3 missing at the beginning and, after it is restored, the accuracy is “only” 33 decimal places. That precision, however, would have been all that Takebe Kenk![]() needed to compute the four corrections he claimed to have computed.
needed to compute the four corrections he claimed to have computed.
10. Since 1868, Owari has formed the western part of Ai Chi Prefecture. It includes the city of Nagoya, where the Atsuta shrine is located.