The history of mathematics: A brief course (2013)
Part V. Islamic Mathematics, 800-1500
Chapter 27. Islamic Geometry
In the Western world, most of the progress in geometry during the millennium that passed between the fall of the Western Roman Empire and the fall of the Eastern Empire occurred among the Muslim and Jewish mathematicians of Baghdad, Samarkand, Cordoba, and other places. This work had some features of Euclid's style and some of Heron's. Matvievskaya (1999) has studied the extensive commentaries on the tenth book of Euclid's Elements written by Muslim scholars from the ninth through twelfth centuries and concluded that while formally preserving a Euclidean distinction between magnitude and number, they actually operated with quadratic and quartic irrationals as if they were numbers.
27.1 The Parallel Postulate
The Islamic mathematicians continued the later Hellenistic speculation on Euclid's parallel postulate. According to Sabra (1969), this topic came into Islamic mathematics through a commentary by Simplicius on Book 1 of the Elements, whose Greek original is lost, although an Arabic translation exists. In fact, Sabra found a manuscript that contains Simplicius' attempted proof. The reworking of this topic by Islamic mathematicians consisted of a criticism of Simplicius' argument followed by attempts to repair its defects. Gray (1989, pp. 42–54) presents a number of these arguments, beginning with the ninth-century mathematician al-Gauhari. Al-Gauhari attempted to show that two lines constructed so as to be parallel, as in Proposition 27 of Book 1 of the Elements must also be equidistant at all points. If he had succeeded, he would indeed have proved the parallel postulate.
27.2 Thabit ibn-Qurra
Thabit ibn-Qurra, whose revision of the Arabic translation of Euclid became a standard in the Muslim world, also joined the debate over the parallel postulate. According to Gray (1989, pp. 43–44), he considered a solid body moving without rotating so that one of its points P traverses a straight line. He claimed that the other points in the body would also move along straight lines, and obviously they would remain equidistant from the line generated by the point P. By regarding these lines as completed loci, he avoided a certain objection that could be made to a later argument of ibn al-Haytham, discussed below. Thabit ibn-Qurra's work on this problem was ground-breaking in a number of ways, anticipating much that is usually credited to the eighteenth-century mathematicians Lambert and Saccheri. He proved, for example, that if a quadrilateral has two equal adjacent angles, and the sides not common to these two angles are equal, then the other two angles are also equal to each other. In the case when the equal angles are right angles, such a figure is called—unjustly, we may say—a Saccheri quadrilateral, after Giovanni Saccheri (1667–1733), who, like Thabit ibn-Qurra, developed it in an attempt to prove the parallel postulate. Gray prefers to call it a Thabit quadrilateral, and we shall use this name. Thabit ibn-Qurra's proof amounted to the claim that a perpendicular drawn from one leg of such a quadrilateral to the opposite leg would also be perpendicular to the leg from which it was drawn. Such a figure, a quadrilateral having three right angles, or half of a Thabit quadrilateral, is now called—again, unjustly—a Lambert quadrilateral, after Johann Heinrich Lambert (1728–1777), who used it for the same purpose. We should probably call it a semi-Thabit quadrilateral. Thabit's claim is that either type of Thabit quadrilateral is in fact a rectangle. If this conclusion is granted, it follows by consideration of the diagonals of a rectangle that the sum of the acute angles in a right triangle is a right angle, and this fact makes Thabit's proof of the parallel postulate work.
The argument of Thabit ibn-Qurra, according to Gray, is illustrated in Fig. 27.1.1 Given three lines l, m, and n such that l is perpendicular to n at E and m intersects it at A, making an acute angle, let W be any point on m above nand draw a perpendicular WZ from W to n. If E is between A and Z, then l must intersect m by virtue of what is now called Pasch's theorem, named after Moritz Pasch (1843–1930), who stated it in 1882. This theorem asserts that a line intersecting the interior of one side of a triangle must intersect at least one other side. That much of the argument would be uncontroversial. The difficult part occurs when Z is between A and E. Thabit ibn-Qurra argued as follows. By Archimedes' principle, some multiple of AZ, say AH, exceeds AE, so that E lies between A and H. Now by drawing a perpendicular HK to n at H, making HK equal to ZW, and joining WK, we have a Thabit quadrilateral WZHK, which Thabit ibn-Qurra thought he had proved to be a rectangle. Then, if X is chosen so that AW = WX and a perpendicular XU is drawn to WK, the triangles AWZ and WXU will be congruent because ∠ZWU is a right angle, and the sum of the acute angles of a right triangle is a right angle. Thus, because angles AWZ and WXU are both complementary to angle XWU, they are equal. It follows that ![]() AZW
AZW ![]()
![]() WUX by the angle–angle–side criterion. Then WU will equal AZ. We can then start over, since WK will be less than AH by a length equal to AZ. In this way, in a finite number of steps, we will reach a point N on line m that is also on the extension of HK. Hence m contains points on both sides of l and therefore intersects l.
WUX by the angle–angle–side criterion. Then WU will equal AZ. We can then start over, since WK will be less than AH by a length equal to AZ. In this way, in a finite number of steps, we will reach a point N on line m that is also on the extension of HK. Hence m contains points on both sides of l and therefore intersects l.
Figure 27.1 Thabit ibn-Qurra's attempted proof of the parallel postulate.
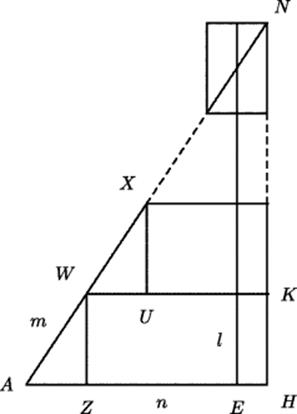
Gray has called Thabit ibn-Qurra's mistake “an interesting and deep one.” It makes use of motion in geometry in a way that seems to be implied by Euclid's own arguments involving coinciding figures; that is, that they can be moved without changing their size or shape. Euclid makes this assumption in Proposition 4 of Book 1, where he “proves” the side–angle–side criterion for congruence by superposing one triangle on another. He does not speak explicitly of moving a triangle, but how else is one to imagine this superposition taking place?
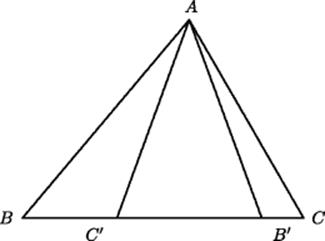
Thabit ibn-Qurra also created the following generalization of the Pythagorean theorem. Consider a triangle ABC whose longest side is BC. Copy angle B with A as vertex and AC as one side, extending the other side to meet BC in point C', and then copy angle C with A as vertex and BA as one side, extending the other side to meet BC in point B', so that angle AB' B and angle AC' C both equal angle A. It then follows that the triangles B' AB and CAC' are both similar to the original triangle ABC, and so ![]() and
and ![]() , hence
, hence
![]()
The case when angle A is acute is shown in Fig. 27.2.
Figure 27.2 Thabit ibn-Qurra's Pythagorean theorem.
27.3 Al-Biruni: Trigonometry
The Islamic mathematicians became familiar with both the chord tables of Ptolemy and the sine tables of Aryabhata I. They used both in their work, but it was the sine function that they developed most fully, eventually creating all six of the ratios that we now call trigonometric functions (although these functions were lines rather than ratios to them). For the sine function, they took over the Sanskrit term jya, meaning bowstring, in its variant form jiva, and wrote it in the Arabic alphabet, without vowels, as j-y-b. This foreign word eventually became conflated with an Arabic word jayb, which means the pocket in a garment. According to Plofker (2009, p. 257), al-Biruni wrote that the Hindus.
. . .call the half-Chords juy![]() b [plural of jayb], for the name of the Chord in the Indian [language] was jiba. . .
b [plural of jayb], for the name of the Chord in the Indian [language] was jiba. . .
It was this Arabic word that eventually came to be translated into Latin as sinus, a word that also means a pocket or cavity.2
27.4 Al-Kuhi
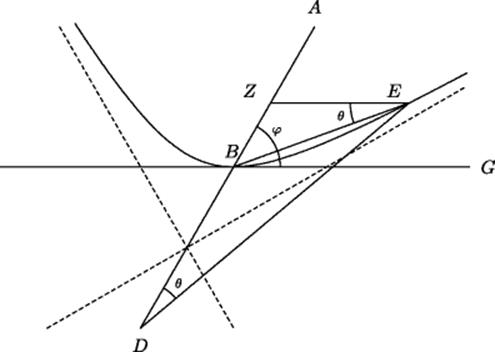
A mathematician who devoted himself almost entirely to geometry was Abu Sahl al-Kuhi (ca. 940–ca. 1000), the author of many works, of which some 30 survive today. Berggren (1989), who has edited these manuscripts, notes that 14 of them deal with problems inspired by the reading of Euclid, Archimedes, and Apollonius, while 11 others are devoted to problems involving the compass, spherical trigonometry, and the theory of the astrolabe. Berggren presents as an example of al-Kuhi's work the angle trisection shown in Fig. 27.3. In that figure the angle ϕ to be trisected is ABG, with the base BG horizontal. The idea of the trisection is to extend side AB any convenient distance to D. At the midpoint of BD, draw a pair of mutually perpendicular lines, one of which makes an angle with the horizontal equal to ϕ/2. Next, draw the rectangular hyperbola through B having those lines as asymptotes. Then BE is drawn equal to BD. That is, a circle through D with center at B is drawn, and its intersection with the hyperbola is labeled E. Finally, EZ is drawn parallel to BG. It then follows that ϕ = ∠ AZE = ∠ ZBE + ∠ ZEB = 3θ, as required. (The difficult part of this proof lies in showing that ∠ZEB = ∠ BDE, as marked in Fig. 27.3.)
Figure 27.3 Al-Kuhi's angle trisection.
27.5 Al-Haytham and Ibn-Sahl
Abu Ali ibn al-Haytham, known in the West as Alhazen, was the author of more than 90 books, 55 of which survive.3 His mathematical prowess is shown by his ambitious attempt to reconstruct the lost Book 8 of Apollonius' Conics. His most famous book is his Treatise on Optics (Kitab al-Manazir) in seven volumes. The fifth volume contains the problem known as Alhazen's problem: Given the location of a surface, an object, and an observer, find the point on the surface at which a light ray from the object will be reflected to the observer. Rashed (1990) points out that burning-mirror problems of this sort had been studied extensively by Muslim scholars, especially by Abu Saad ibn Sahl (940–1000) some decades before al-Haytham.
Rashed (1990, p. 478) discovered a manuscript in Teheran written by ibn Sahl containing the law of refraction known in Europe as Snell's law, after Willebrod Snell (1591–1626) or Descartes' law.4 The law of refraction as given by Ptolemy in the form of a table of values of the angle of refraction and the angle of incidence implied that the angle of refraction was a quadratic function of the angle of incidence. The actual relation is that the ratio of the sines of the two angles is a constant for refraction at the interface between two different media. What ibn Sahl and ibn al-Haytham knew was that the ratio of the two sines at a point where two media meet was the same whatever the angle of incidence happened to be. The seventeenth-century rediscoverers deduced theoretically that this ratio is the ratio of the speeds with which light propagates in the two media. Fermat, as we shall see in Chapter 34, showed that, given this connection, the actual time of travel from a point in one medium to a point in another is minimized.
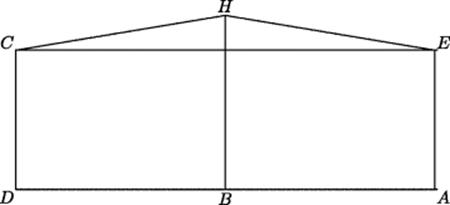
Al-Haytham also attempted to prove the parallel postulate. According to Gray (1989, p. 45), the argument given by al-Haytham in his Commentary on the Premises to Euclid's Book The Elements, and later in his Book on the Resolution of Doubts, was based on the idea of translating a line perpendicular to a given line in such a way that it always remains perpendicular. The idea is that the endpoint of the line must trace a straight line parallel to the directing line. The idea of the proof is shown in Fig. 27.4. Al-Haytham constructs a Thabit quadrilateral CDAE and imagines the side CD moving toward the opposite side EA, with D remaining on the base line, and the side remaining perpendicular at each instant of time. Obviously then the point C will remain equidistant from the base DA at all times. Al-Haytham was sure that C would move along the line CE, and could never, for example, be at a point H above that line. Unfortunately, that seemingly obvious and very intuitive conviction is precisely the point at issue in the parallel postulate.
Figure 27.4 Ibn al-Haytham's attempted proof of the parallel postulate.
27.6 Omar Khayyam
In his paper Discussion of difficulties in Euclid (Amir-Moez, 1959), Omar Khayyam raised a number of questions about al-Haytham's argument. He asked how a line could move while remaining perpendicular to a given line and, more generally, how geometry and motion could be connected. Even admitting that Euclid allowed a line to be generated by a moving point and a surface by a moving line, he pointed out that al-Haytham was requiring something more in demanding that one line remain perpendicular to another at each instant during its motion.5
Having refuted al-Haytham's proof, Omar Khayyam himself attempted a proof (Amir-Moez, 1959) based on a proposition that he claimed Aristotle had proved: If two lines converge, they will (eventually) intersect. This claim raises an interesting question, since, as we have seen, Aristotle did not accept the arguments given by scholars in Plato's Academy to prove that parallel lines exist. Given his disbelief in a completed infinity, he probably would have liked an argument proving that converging lines must intersect. Although none of the writings now attributed to Aristotle contain such an argument, Gray (1989, p. 47) suggests that Omar Khayyam may have had access to Aristotelian treatises that no longer exist. Omar Khayyam concluded on the basis of Aristotle's authority that two lines that converge on one side of a transversal must diverge on the other side. With that, having proved correctly that the perpendicular bisector of the base of a Thabit quadrilateral is also the perpendicular bisector of the summit, Omar Khayyam concluded that the base and summit could not diverge on either side, and hence must be equidistant. Like Thabit ibn-Qurra's proof, his proof depended on building one Thabit quadrilateral on top of another by doubling the common bisector of the base and summit, then crossing its endpoint with a perpendicular which (he said) would intersect the extensions of the lateral sides. Unfortunately, if that procedure is repeated often enough in hyperbolic geometry, those intersections will not occur.
All of these mathematicians were well versed in the Euclidean tradition of geometry. In the preface to his book on algebra, Omar Khayyam says that no one should attempt to read it who has not already read Euclid's Elements and Data and the first two books of Apollonius' Conics. His reason for requiring this background was that he intended to use conic sections to solve cubic and quartic equations geometrically. This book contains Euclidean rigor attached to algebra in a way that fits equally well into the history of both algebra and geometry. In other places, it seems clear that Omar Khayyam was posing geometric problems for the sake of getting interesting equations to solve, as, for example, in the problem mentioned in the previous chapter of finding the point on a circle such that the perpendicular from the point to a radius has the same ratio to the radius that the two segments into which it divides the radius have to each other.
As his work on the parallel postulate shows, Omar Khayyam was very interested in logical niceties. In the preface to his Algebra and elsewhere [for example, Amir-Moez (1963, p. 328)] he shows his adherence to Euclidean standards, denying the reality of a fourth dimension:
If the algebraist were to use the square of the square in measuring areas, his result would be figurative [theoretical] and not real, because it is impossible to consider the square of the square as a magnitude of a measurable nature. . .This is even more true in the case of higher powers. [Kasir, 1931, p. 48]
27.7 Nasir al-Din al-Tusi
The thirteenth century was disruptive to the Islamic world. This was the time of the Mongol expansion, which brought the conquest of China in the early part of the century, then the conquest of Kievan Rus in 1243, and, finally, the sack of Baghdad in 1258. Despite the turbulent times, the astronomer–mathematician Nasir al-Din al-Tusi (1201–1274) managed to produce some very good mathematics. Al-Tusi was treated with respect by the Mongol conqueror of Baghdad, who even built for him an astronomical observatory, at which he made years of accurate observations and improved the models in Ptolemy's Almagest. Al-Tusi continued the Muslim work on the problem of the parallel postulate. According to Gray (1989, pp. 50–51), al-Tusi's proof followed the route of proving that the summit angles of a Thabit quadrilateral are right angles. He showed by arguments that Euclid would have accepted that they cannot be obtuse angles, since, if they were, the summit would diverge from the base as a point moves from either summit vertex toward the other. Similarly, he claimed, they could not be acute, since in that case the summit would converge toward the base as a point moves from either summit vertex toward the other. Having thus argued that a Thabit quadrilateral must be a rectangle, he could give a proof similar to that of Thabit ibn-Qurra to establish the parallel postulate.
In a treatise on quadrilaterals written in 1260, al-Tusi also reworked the trigonometry inherited from the Greeks and Hindus and developed by his predecessors in the Muslim world, including all six triangle ratios that we know today as the trigonometric functions. In particular, he gave the law of sines for spherical triangles, which states that the sines of great-circle arcs forming a spherical triangle are proportional to the sines of their opposite angles. According to Hairetdinova (1986), trigonometry had been developing in the Muslim world for some centuries before this time, and in fact the mathematician Abu Abdullah al-Jayyani (989–1079), who lived in the Caliphate of Cordoba, wrote The Book on Unknown Arcs of a Sphere, a treatise on plane and spherical trigonometry. Significantly, he treated ratios of lines as numbers, in accordance with the evolution of thought on this subject in the Muslim world. Like other Muslim mathematicians, though, he does not use negative numbers. As Hairetdinova mentions, there is evidence of Muslim influence in the first trigonometry treatise written by Europeans, the book De triangulis omnimodis by Regiomontanus, (Johann Müller, 1436–1476) whose exposition of plane trigonometry closely follows that of al-Jayyani.
Among these and many other discoveries, al-Tusi discovered the interesting theorem that if a circle rolls without slipping inside a circle twice as large, each point on the smaller circle moves back and forth along a diameter of the larger circle. This fact is easy to prove and an interesting exercise in geometry. It has obvious applications in geometric astronomy, and was rediscovered three centuries later by Nicolaus Copernicus (1473–1543) and used in Book 3, Chapter 4 of his De revolutionibus.
Problems and Questions
Mathematical Problems
27.1 Explain how Thabit ibn-Qurra's generalization of the Pythagorean theorem reduces to that theorem when angle A is a right angle. What does the figure look like if angle A is obtuse? Is there an analogous theorem if BC is not the longest side of the triangle?
27.2 Al-Haytham's attempted proof of the parallel postulate is fallacious because in non-Euclidean geometry two straight lines cannot be equidistant at all points. Thus in a non-Euclidean space the two rails of a railroad cannot both be straight lines. Assuming Newton's laws of motion (an object that does not move in a straight line must be subject to some force), show that in a non-Euclidean universe one of the wheels in a pair of opposite wheels on a train must be subject to some unbalanced force at all times. [Note: The spherical earth that we live on happens to be non-Euclidean. Therefore a pair of opposite wheels on a train cannot both be moving in a great circle on the earth's surface at any time.]
27.3 A two-part question: (1) Prove that in both hyperbolic and Euclidean geometry, if a line passes through the midpoint of side AB of triangle ABC and is perpendicular to the perpendicular bisector of the side BC, then it also passes through the midpoint of AC. [Hint: This is easier than it looks: Consider the line that does pass through both midpoints, and show that it is perpendicular to the perpendicular bisector of BC; then argue that there is only one line passing through the midpoint of AB that is perpendicular to the perpendicular bisector of BC.] (2) Use the previous result to prove, independently of the parallel postulate, that the line joining the midpoints of the lateral sides of a Thabit (Saccheri) quadrilateral bisects both diagonals. (In Euclidean geometry, where a Thabit quadrilateral is a rectangle, the diagonals bisect each other; this is not the case in non-Euclidean geometries.)
Historical Questions
27.4 What efforts were made by the Islamic geometers to clarify the theory of parallel lines and the parallel postulate of Euclid?
27.5 What generalization of the Pythagorean theorem is due to Thabit ibn-Qurra?
27.6 What advances in trigonometry are due to Nasir al-Din al-Tusi?
Questions for Reflection
27.7 Why was speculation on the theory of parallel lines confined to the Hellenistic and Islamic geometers? Why was this problem never addressed by the Indian, Chinese, or Japanese mathematicians?
27.8 Why was al-Haytham's attempt to prove the parallel postulate fallacious?
27.9 What applications can you find for Nasir al-Tusi's theorem about a circle rolling without slipping inside a circle whose radius equals the diameter of the inner circle? (Imagine the circles roughened so has to have gear teeth of the same size that mesh. What use could you make of such a linkage?)
Notes
1. We are supplementing the figure and adding steps to the argument for the sake of clarity.
2. Contrast this Latin term with the names for the other two trigonometric functions, tangent (touching), and secant (cutting), both of which have obvious geometric meanings.
3. Rashed (1989) suggested that these works and the biographical information about al-Haytham may actually refer to two different people. The opposite view was maintained by Sabra (1998).
4. According to Guizal and Dudley, this law was stated by Thomas Harriot (1560–1621) in 1602.
5. Omar Khayyam's objection is right on target from the point of view of modern physics. If the special theory of relativity is correct, no sense can be attached to the statement that two events occurring at different places are simultaneous. One observer may find them so, while another does not agree. The same objection applies to Thabit ibn-Qurra's argument, which assumes a rigid body. In special relativity, rigid bodies do not exist. What al-Haytham did was to ignore all points from the moving solid except those lying along a certain line.