The history of mathematics: A brief course (2013)
Part VI. European Mathematics, 500-1900
Chapter 31. Renaissance Art and Geometry
It is said that Euclid's geometry is tactile rather than visual, since the theorems tell you what you can measure and feel with your hands, not what your eye sees. It is a commonplace that a circle seen from any position except a point on the line through its center perpendicular to its plane appears to be an ellipse. If figures did not distort in this way when seen in perspective, we would have a very difficult time navigating through the world. We are so accustomed to adjusting our judgments of what we see that we usually recognize a circle automatically when we see it, even from an angle. The distortion is an essential element of our perception of depth.
31.1 The Greek Foundations
Renaissance geometers and artists built on a foundation that the Greeks had laid for them in the areas of regular and semiregular solids, conic sections, and perspective. These last two have a particularly intimate relationship.
To take the simpler subject first, Euclid had discussed the five regular solids in the last three books of his Elements, finding the proportions between their edges and the radii of their inscribed and circumscribed spheres and showing that there can be only five such solids. He also discussed some semiregular solids such as prisms and pyramids, which would be needed later in applications of the method of exhaustion to spheres. The Renaissance geometers and artists expanded the limited circle of ideas around regular polyhedra to a large number of semiregular figures.
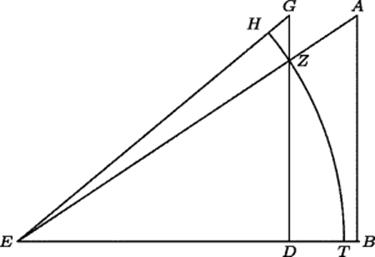
Euclid also wrote a book on optics in which he discussed the apparent reduction in size of objects as they move away from the observer. He used his “tactile” geometry to compare their actual sizes with their apparent sizes. The apparent sizes of the two equal vertical lines DG and AB in Fig. 31.1, as seen by the eye located at E, is measured by the angles they subtend, and thus are proportional to the arcs TH and TZ or, equivalently, to the circular sectors THE and TZE. But DE : BE : : DZ : BA : : DZ : DG. This last ratio, in turn, is proportional to the areas of the triangles EDZ and EDG. But EDZ is smaller than sector TZE, while EZG is larger than sector ZHE. It follows that EZG : EDZ > ZHE : TZE, and adding 1 to both sides implies that EDG : EDZ > THE : TZE. Thus, the ratio of the apparent size of DG to the apparent size of AB, which is the ratio THE : TZE, is smaller than the ratio of EDG to EDZ, and hence also smaller than the ratio of BE to DE. In other words, the apparent “shrinkage” with distance is not inversely proportional to the distance. An object moved so as to double its distance from the eye appears to be more thanhalf of its previous size.
Figure 31.1 Apparent shrinkage of a vertical line as its distance from the observer increases.
Artists, especially those of the Italian Renaissance, used these principles to create paintings that were astoundingly realistic. As Leonardo da Vinci (1452–1519) said, “the primary task of a painter is to make a flat plane look like a body seen in relief projecting out of it.” Many records of the principles by which this effect was achieved have survived, including treatises of Leonardo himself and a painter's manual by Albrecht Dürer (1471–1528), first published in 1525. Over a period of several centuries, these principles gave rise to the subject now known as projective geometry.
31.2 The Renaissance Artists and Geometers
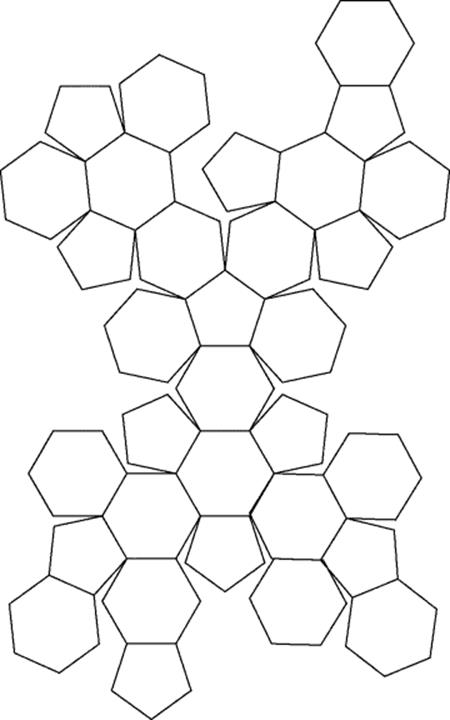
The revival of interest in ancient culture in general during the Renaissance naturally carried with it an interest in geometry. The famous artist Piero della Francesca (ca. 1410–1492) was inspired by the writings of Leonardo of Pisa and others to write treatises on arithmetic and the five regular solids. The scholar Luca Pacioli (1445–1517), who was influenced by Piero della Francesca and was a friend of Leonardo da Vinci, published a comprehensive treatise on arithmetic and geometry in 1494, and a second book, De divina proportione, in 1509. He gave the name Divine Proportion to what is now called the Golden Section, the division of a line into mean and extreme ratios. Interest in the five regular solids branched out into an interest in semiregular solids. Leonardo da Vinci designed wooden models of these, which were depicted in Pacioli's treatise. A typical example is the truncated icosahedron, formed by cutting off the 12 vertices of an icosahedron so as to produce 12 pentagons. If the vertices are cut off at just the right distance, the middle portions of the edges of the original triangles will be exactly equal to the sides of the pentagons that replace the vertices of the triangles, so that the remaining portion of the triangular face will become a regular hexagon. The resulting figure, consisting of 20 hexagons and 12 pentagons, is the truncated icosahedron.
The regular and semiregular solids formed an important part of Dürer's 1525 manual for painters. He showed how to cut out a paper model of a truncated icosahedron (Fig. 31.2). The solid, although not the name, has become very familiar to modern people through its application in athletics (the ball used in playing soccer) and organic chemistry (a molecule of C60, known as buckminsterfullerene).
Figure 31.2 Dürer's paper model of a truncated icosahedron.
31.3 Projective Properties
Projective geometry studies the relations among figures that remain constant in perspective. Among these things are points and lines, the number of intersections of lines and circles, and consequently also such things as parallelism (but not always, unless certain “points at infinity” remain at infinity) and tangency, but not things that depend on shape, such as angles or circles. Like the result from Euclid's Optics discussed above, its methods come out of Euclidean geometry, but explore new implications of the Euclidean definitions and assumptions.
Two modern applications ofthe truncated icosahedron: a molecule of C60,buckminsterfullerene (a “buckyball”); a soccer ball.

A circle seen in perspective is anellipse.
A nonobvious property that is preserved in projection is what is now called the cross-ratio of four points on a line.1 If A, B, C, and D are four points on a line, with B and C both between A and D and C between B and D, their cross-ratio is
![]()
If the rays PA, PB, PC, and PD from a point P intersect a second line in points A', B', C', and D', the cross-ratio of these new points is the same as that of the original four points. Coolidge (1940, p. 88) speculated that Euclid may have known about the cross-ratio, and he asserted that the early second-century mathematician Menelaus did know about it. The concept was introduced by Pappus in Book 7 of the Synagomacr1.gifg![]() (Jones, 1986). It is preserved by fractional-linear transformations such as those introduced by Newton (see Chapter 38) and is used in defining distance in the models of non-Euclidean geometry (see Chapter 40).
(Jones, 1986). It is preserved by fractional-linear transformations such as those introduced by Newton (see Chapter 38) and is used in defining distance in the models of non-Euclidean geometry (see Chapter 40).
A geometric description of perspective was written by Leon Battista Alberti (1404–1472) in 1435 in a Latin treatise entitled De pictura, reworked by him in Italian the following year as Della pittura and published posthumously in 1511. If the eye is at fixed height above a horizontal plane, parallel horizontal lines in that plane receding from the imagined point where the eye is located can be drawn as rays emanating from a point (the vanishing point) at the same height above the plane, giving the illusion that the vanishing point is infinitely distant. The application to art is obvious: Since the canvas can be thought of as a window through which the scene is viewed, if you want to draw parallel horizontal lines as they would appear through a window, you must draw them as if they all converged on the vanishing point. Thus, a family of lines having a common property (being parallel to one another) projects to a family having a different common property (passing through a common point). Obviously, lines remain lines under such a projection. However, perpendicular lines will not remain perpendicular, nor will circles remain circles.
31.3.1 Girard Desargues
The mathematical development of the theory of projection began with the work of Girard Desargues (1593–1662). In 1636, Desargues published a pamphlet with the ponderous title An Example of One of the General Methods of S.G.D.L.2 Applied to the Practice of Perspective Without the Use of Any Third Point, Whether of Distance or Any Other Kind, Lying Outside the Work Area. The reference to a “third point” was aimed at the primary disadvantage of Alberti's rules, the need to use a point not on the canvas in order to get the perspective correct. Three years later he produced a Rough Draft of an Essay on the Consequences of Intersecting a Cone with a Plane. In both works, written in French rather than the more customary Latin, he took advantage of the vernacular to invent new names, not only for the conic sections,3 as Dürer had done, but also for a large number of concepts that called attention to particular aspects of the distribution and proportions of points and lines. He was particularly fond of botanical names4 and included tree, trunk, branch, shoot, and stem, among many other neologisms. Although the new language might seem distracting, using standard terms for what he had in mind would have been misleading, since the theory he was constructing unified concepts that had been distinct before. For example, he realized that a cylinder could be regarded as a limiting case of a cone, and so he gave the name scroll to the class consisting of both surfaces. Desargues had very little need to refer to any specific conic section; his theorems applied to all of them equally. As he said (Field and Gray, 1987, p. 102—I have changed their roll to scroll):
The most remarkable properties of the sections of a scroll are common to all types, and the names Ellipse, Parabola, and Hyperbola have been given them only on account of matters extraneous to them and to their nature.
Desargues was among the first to regard lines as infinitely long, in the modern way. In fact, he opens his treatise by saying that he will consider both the infinitely large and the infinitely small in his work, and he says that “in this work every straight line is, if necessary, taken to be produced to infinity in both directions.” He also had the important insight that a family of parallel lines and a family of lines with a common point of intersection have similar properties. He said that lines belonged to the same order5 if either they all intersected at a common point or were all mutually parallel. This term was introduced “[to] indicate that in the one case as well as in the other, it is as if they all converged to the same place” [emphasis added].
Although Desargues' terminology was messy, his Rough Draft contained some elegant theorems about points on conics. Two significant results are the following6:
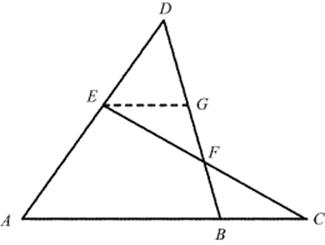
First: If four lines in a plane intersect two at a time, and the points of intersection on the first line are A, B, and C, with B between A and C, and the lines through A and B intersect in the point D, those through A and C in E and those through B and C in F, then
(31.1) ![]()
The situation here was described by Pappus, and the result is also known as Menelaus' theorem. The proof involves drawing the line through E parallel to AB, meeting BD in a point G, and then using the similarity of triangles EGFand CBF and of triangles DEG and DAB, as in Fig. 31.3. From Eq. (31.1) it is easy to deduce that BD · AE · CF = BF · AD · CE. Klein (1926, p. 80) attributes this form of the theorem to Lazare Carnot (1753–1823).
Figure 31.3 Menelaus' theorem for a plane triangle.
Second: The converse of this statement is also true, and can be interpreted as stating that three points lie on a line. That is, if ADB is a triangle, and E and F are points on AD and BD respectively such that AD : AE < BD : BF, then the line through E and F meets the extension of AB on the side of B in a point C, which is characterized as the only point on the line EF satisfying Eq. (31.1).
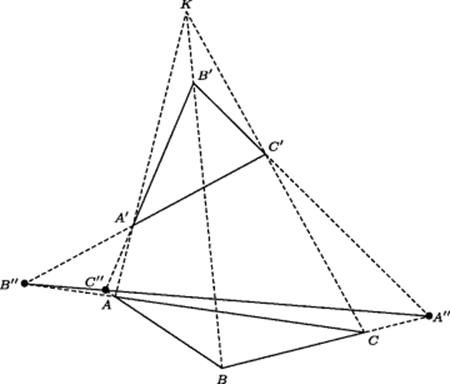
In 1648 the engraver Abraham Bosse (1602–1676), who was an enthusiastic supporter of Desargues' new ideas, published La perspective de Mr Desargues, in which he reworked these ideas in detail. Near the end of the book he published the theorem that is now known as Desargues' theorem. Like Desargues' work, Bosse's statement of the theorem is a tangled mess involving ten points denoted by four uppercase letters and six lowercase letters. The points lie on nine different lines. When suitably clarified, the theorem states that if the lines joining the three pairs of vertices from two different triangles intersect in a common point, the pairs of lines containing the corresponding sides of these triangles meet in three points all on the same line. This result is easy to establish if the triangles lie in different planes, since the three points must lie on the line of intersection of the two planes containing the triangles, as shown in Fig. 31.4.
Figure 31.4 Desargues' theorem for triangles lying in different planes.
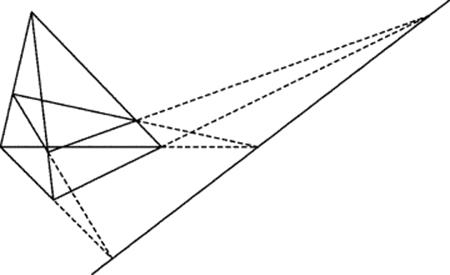
For two triangles in the same plane, the theorem, illustrated in Fig. 31.5, was proved by Bosse by applying Menelaus' theorem to the three sets of collinear points {A ”, C, B}, {B ”, A, C}, and {C ”, A, B}, with K as the third vertex of the triangle whose base ends in the second and third points in all three cases. (There is no other conceivable way to proceed, so that in a sense the proof is a mere computation.) When the ratios AK : AA', BK : BB', and CK : CC' are eliminated from the three equations that result, what is left is the equation
![]()
Having received a copy of this work from the Parisian mathematician Marin Mersenne (1588–1648), René Descartes (1596–1654) took the word draft literally and regarded it as a proposal to write a treatise—which it may have been—such as a modern author would address to a publisher, and a publisher would send to an expert for review. He wrote to Desargues to express his opinion of “what I can conjecture of the Treatise on Conic Sections, of which [Mersenne] sent me the Draft.” Descartes' “review” of the work contained the kind of advice reviewers still give: that the author should decide more definitely who the intended audience was. As he said, if Desargues was aiming to present new ideas to scholars, there was no need to invent new terms for familiar concepts. On the other hand, if the book was aimed at the general public, it would need to be very thick, since everything would have to be explained in great detail (Field and Gray, 1987, p. 176).
Figure 31.5 Desargues' theorem for two triangles in the same plane.
31.3.2 Blaise Pascal
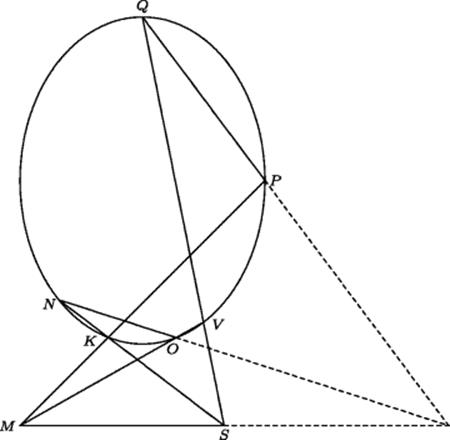
Desargues' work was read by a teenage boy named Blaise Pascal (1623–1662), who was to become famous for his mathematical work and renowned for his Pensées (Meditations), which are still read by many people today for inspiration. He began working on the project of writing his own treatise on conics. Being very young, he was humble and merely sketched what he planned to do, saying that his mistrust of his own abilities inclined him to submit the proposal to experts, and “if someone thinks the subject worth pursuing, we shall try to carry it out to the extent that God gives us the strength.” Pascal admired Desargues' work very much, saying that he owed “what little I have discovered to his writings” and would imitate Desargues' methods, which he considered especially important because they treated conic sections without introducing the extraneous axial section of the cone. He used much of Desargues' notation for points and lines, including the word order for a family of concurrent lines. His work, like that of Desargues, remained only a draft, although Struik (1986, p. 165) reports that Pascal worked further on this project and that Leibniz saw a manuscript of it—not the rough draft, apparently—in 1676. All that has been preserved, however, is the rough draft. That draft contains several results in the spirit of Desargues, one of which, called by Pascal a “third lemma,” is well known. In the notation of Fig. 31.6, where four lines MK, MV, SK, and SV are drawn and then a conic is passed through K and V meeting these four lines in four other points P, O, N, and Qrespectively, Pascal asserted that the lines PQ, NO, and MS would be concurrent (belong to the same order).
Figure 31.6 Pascal's third lemma.
Problems and Questions
Mathematical Problems
31.1 Prove Menelaus' theorem and its converse. What happens if the points E and F are such that AD : AE : : BD : BE? (Euclid gave the answer to this question.)
31.2 Use Menelaus' theorem to prove that two medians of a triangle intersect in a point that divides each in the ratio of 1:2. You may assume that all three medians are concurrent, as this is not difficult to prove.
31.3 Euclid showed that the angle subtended by an object of height h at distance d is larger at larger distances than it would be if it were merely inversely proportional to d. In other words, there is no constant k such that
![]()
and in fact αd/h is an increasing function of d when h is fixed.7 Show that, if α is measured in degrees, then
![]()
Historical Questions
31.4 Which Renaissance artists studied geometry for the purpose of creating paintings, buildings, and sculpture?
31.5 How does projective geometry differ from Euclidean geometry?
31.6 Where was the modern notion of a line as “infinitely long” first stated?
Questions for Reflection
31.7 What considerations may have led the Renaissance artists to renew their interest in geometry and apply it to their art?
31.8 One of Dürer's devices for drawing in perspective involves a thread passing through a rectangular frame with a gate hinged on one side of it containing the canvas. On the opposite side of the frame from the object being painted, the thread passes over a pulley, which constitutes the vanishing point for the perspective. The end of the thread is held against a point to be mapped onto the canvas. Crosshairs are stuck on the frame to mark the point where the thread passes through it. The thread is then removed, the gate is closed, and a mark is made at the point where the crosshairs meet. Painting in this way is a two-person job, requiring one person to hold the end of the thread against the object and a second person to set the crosshairs. Which of these two people counts as the artist, and which as the assistant?
31.9 In what sense are lines and points treated symmetrically in projective geometry. (Think of Desargues' theorem.)
Notes
1. Although this ratio has been used for centuries, the name it now bears in English seems to go back only to an 1869 treatise on dynamics by William Kingdon Clifford (1845–1879). Before that it was called the anharmonic ratio, a phrase translated from an 1837 French treatise by Michel Chasles (1809–1880).
2. Sieur Girard Desargues Lyonnois.
3. He gave the standard names to the conic sections themselves, but suggested deficit, equalation, and exceedence as alternatives.
4. Ivins (1947, cited by Field and Gray, 1987, p. 62) suggested that these names were inspired by similar names in Alberti's treatise.
5. Now called a pencil or sheaf.
6. To keep the reader's eye from getting too tangled up, we shall use standard letters in the statement and figure rather than Desargues' weird mixture of uppercase and lowercase letters and numbers, which almost seems to anticipate the finest principles of computer password selection.
7. In other words, the actual horizontal distance grows faster than the apparent height, measured by α, shrinks. The effect is that horizontal distances appear foreshortened, and things don't appear to be as far away as they actually are. This phenomenon is well-known to anyone who has ever swum across a lake.